北师大版数学(2024)七年级下册全册综合题(精华)(含答案)
文档属性
| 名称 | 北师大版数学(2024)七年级下册全册综合题(精华)(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 544.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-08 12:59:53 | ||
图片预览



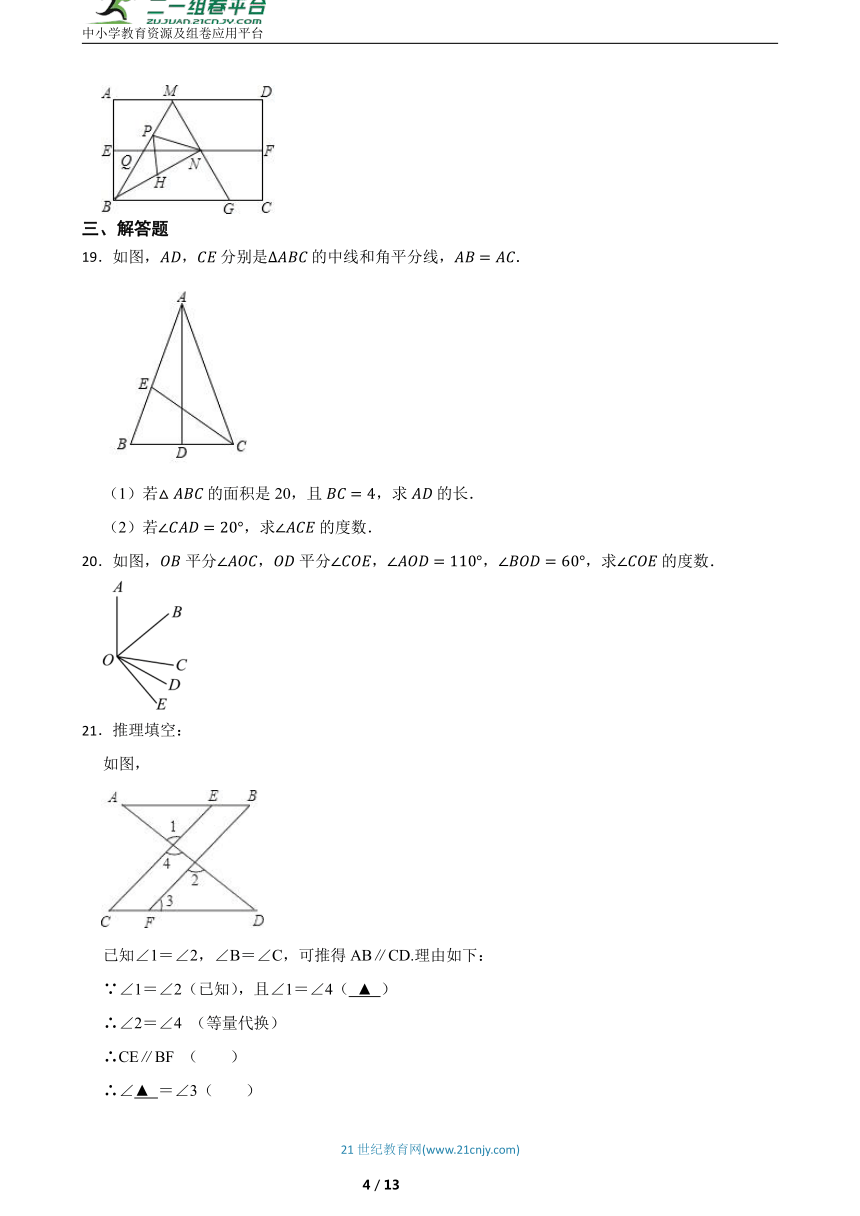
文档简介
中小学教育资源及组卷应用平台
北师大版数学(2024)七年级下册全册综合题(精华)
一、单选题
1.下列说法正确的是( )
A.三条线段首尾顺次相接所组成的图形叫做三角形
B.三角形按边分类可分为三边都不相等的三角形、等腰三角形和等边三角形
C.关于轴对称的两个图形大小不变,形状改变
D.两角和一边对应相等的两个三角形全等
2.如图,直线,被直线所截,下列条件不能证明直线的是( )
A. B. C. D.
3.如图,D是的边上一点,将折叠,使点C落在上的点处,展开后得到折痕,则是的( )
A.中线 B.高线 C.角平分线 D.中位线
4.若,则( )
A. B. C. D.
5.下列交通标志中,是轴对称图形的是( )
A. B.
C. D.
6.下列语句中:
①经过一点有且只有一条直线与已知直线垂直;②过一点有且只有一条直线与已知直线平行;③互为邻补角的两个角的平分线互相垂直;④有公共顶点且相等的角是对顶角,其中错误的个数有( )
A.1个 B.2个 C.3个 D.4个
7.在平面内,将一个直角三角板按如图所示摆放在一组平行线上,若,则的度数是( )
A.35° B.40° C.45° D.50°
8.PM2.5是指大气中直径小于或等于0.000 002 5米的颗粒物,将0.000 002 5用科学记数法表示为( )
A.0.25×10-5 B.2.5×10-6 C.2.5×10-7 D.2.5×10-5
9.在△ABC中,∠BAC=115°,DE、FG分别为AB、AC的垂直平分线,则∠EAG的度数为( )
A.50° B.40° C.30° D.25°
10.在快速计算法中,法国的“小九九”从“一一得一”到“五五二十五”和我国的“小九九”算法是完全一样的,而后面“六到九”的运算就改用手势了.如计算8×9 时,左手伸出3根手指,右手伸出4根手指,两只手伸出手指数的和为7,未伸出手指数的积为2,则8×9=10×7+2=72.那么在计算6×8时,左、右手伸出的手指数应该分别为( )
A.1,3; B.3,1; C.1,4; D.4,1;
二、填空题
11.如图,现给出下列条件∶①,②,③,④.能够得到的条件是(填序号) .
12.已知,计算: .
13.若,则的值是 .
14.某商场为了增加销售额,推出“七月销售大酬宾”活动,其活动内容为:“凡七月份在该商场一次性购物超过100元以上者,超过100元的部分按8.5折优惠.”在大酬宾活动中,小王到该商场为单位购买单价为60元的办公用品x件,则应付货款y(元)与商品件数x的关系式是 .
15.如果关于x的整式和相乘的结果中不包含三次项,那么 .
16.如图,,平分,,.则的度数是 .
17.如图,矩形中,E是的中点,将沿折叠后得到,延长交于点F,若,,则的长为 .
18.如图,四边形ABCD是矩形纸片,AB=2.对折矩形纸片ABCD,使AD与BC重合,折痕为EF;展平后再过点B折叠矩形纸片,使点A落在EF上的点N,折痕BM与EF相交于点Q;再次展平,连接BN,MN,延长MN交BC于点G.有如下结论:
①∠ABN=60°;②AM=1;③QN= ;④△BMG是等边三角形;⑤P为线段BM上一动点,H是BN的中点,则PN+PH的最小值是 .
其中正确结论的序号是 .
三、解答题
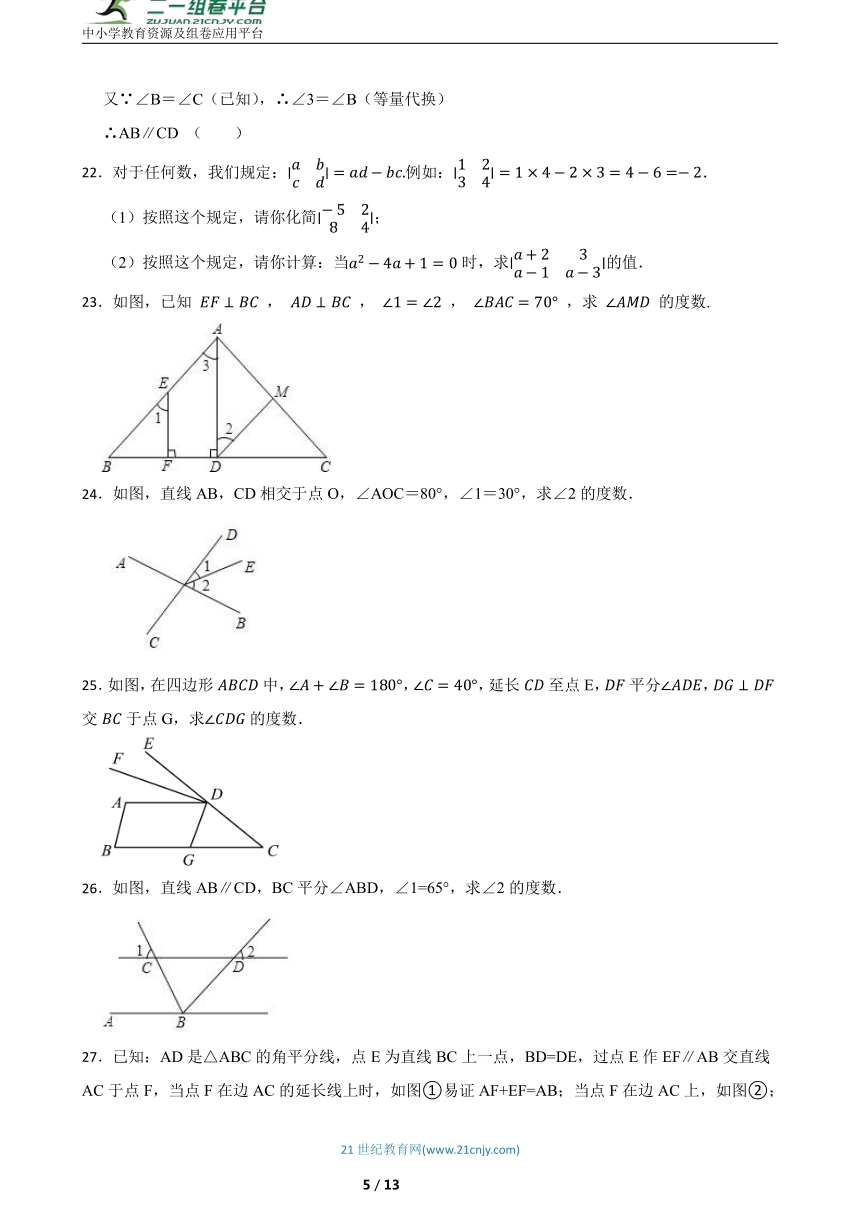
19.如图,,分别是的中线和角平分线,.
(1)若的面积是20,且,求的长.
(2)若,求的度数.
20.如图,平分,平分,,,求的度数.
21.推理填空:
如图,
已知∠1=∠2,∠B=∠C,可推得AB∥CD.理由如下:
∵∠1=∠2(已知),且∠1=∠4( ▲ )
∴∠2=∠4 (等量代换)
∴CE∥BF ( )
∴∠▲ =∠3( )
又∵∠B=∠C(已知),∴∠3=∠B(等量代换)
∴AB∥CD ( )
22.对于任何数,我们规定:例如:.
(1)按照这个规定,请你化简;
(2)按照这个规定,请你计算:当时,求的值.
23.如图,已知 , , , ,求 的度数.
24.如图,直线AB,CD相交于点O,∠AOC=80°,∠1=30°,求∠2的度数.
25.如图,在四边形中,,,延长至点E,平分,交于点G,求的度数.
26.如图,直线AB∥CD,BC平分∠ABD,∠1=65°,求∠2的度数.
27.已知:AD是△ABC的角平分线,点E为直线BC上一点,BD=DE,过点E作EF∥AB交直线AC于点F,当点F在边AC的延长线上时,如图①易证AF+EF=AB;当点F在边AC上,如图②;当点F在边AC的延长线上,AD是△ABC的外角平分线时,如图3.写出AF、EF与AB的数量关系,并对图②进行证明.
28. 已知:点F、点G分别为直线上的点,E为平面内任意一点,连接与直交于点M,.
(1)如图1,求证:;
(2)如图2,和分别平分与,和的反向延长线交于点K,探究和的数量关系,并证明你的结论;
(3)如图3,在(2)的条件下,与交于点N,射线交直线于P,若,求的长.
答案解析部分
1.【答案】D
【知识点】轴对称的性质;三角形相关概念
2.【答案】B
【知识点】平行线的判定;对顶角及其性质
3.【答案】B
【知识点】三角形的角平分线、中线和高;翻折变换(折叠问题)
4.【答案】B
【知识点】多项式除以单项式
5.【答案】D
【知识点】轴对称图形
6.【答案】C
【知识点】垂线的概念;平行公理及推论;对顶角及其性质;邻补角
7.【答案】A
【知识点】平行线的性质
8.【答案】B
【知识点】科学记数法表示大于0且小于1的数
9.【答案】A
【知识点】线段垂直平分线的性质
10.【答案】A
【知识点】有理数的加减乘除混合运算的法则;定义新运算
11.【答案】②③④
【知识点】平行线的判定
12.【答案】5
【知识点】平方差公式及应用
13.【答案】108
【知识点】同底数幂的乘法;幂的乘方运算
14.【答案】
【知识点】用关系式表示变量间的关系
15.【答案】2
【知识点】多项式乘多项式
16.【答案】
【知识点】平行线的性质;角平分线的性质
17.【答案】5
【知识点】直角三角形全等的判定-HL;矩形的性质
18.【答案】①④⑤
【知识点】轴对称的应用-最短距离问题
19.【答案】(1)10
(2)
【知识点】等腰三角形的性质
20.【答案】
【知识点】角的运算;角平分线的性质
21.【答案】解:∵∠1=∠2(已知),且∠1=∠4(对顶角相等),
∴∠2=∠4 (等量代换),
∴CE∥BF (同位角相等,两直线平行),
∴∠C=∠3(两直线平行,同位角相等);
又∵∠B=∠C(已知),
∴∠3=∠B(等量代换),
∴AB∥CD (内错角相等,两直线平行).
【知识点】平行线的判定与性质
22.【答案】(1)由题意得:
(2)由题意得:
,
,
,
原式.
【知识点】多项式乘多项式
23.【答案】解:∵AD⊥BC,EF⊥BC,
∴AD∥EF,
∴∠1=∠BAD,
又∵∠1=∠2,
∴∠2=∠BAD,
∴AB∥DM,
∴∠AMD+∠BAC =180°,
∵ ,
∴∠AMD=180°-∠BAC=180°-70°=110°.
【知识点】平行线的判定与性质
24.【答案】解:∵∠AOC=∠BOD,∠AOC=80°,
∴∠BOD=80°,
∵∠1+∠2=∠BOD,∠1=30°,
∴∠2=∠BOD-∠1=50°.
【知识点】对顶角及其性质
25.【答案】
【知识点】平行线的判定与性质;角平分线的性质
26.【答案】解: ∵AB∥CD,
∴∠1=∠CBA=65°,∠2=∠DBE,
又∵BC平分∠ABD,
∴∠ABD=2∠ABC=130°,
∴∠DBE=180°-∠ABD=180°-130°=50°,
∴∠2=50°.
【知识点】平行线的性质
27.【答案】解:当点F在边AC的延长线上时,延长EF、AD相交于点G,如图:
∵AD是△ABC的角平分线,
∴∠BAD=∠CAD,
∵EF∥AB,
∴∠BAD=∠G,∠B=∠E,
∴∠CAD=∠G,
∴FA=FG,
在△ABD和△GED中,,
∴△ABD≌△GED(AAS),
∴AB=EG,
∴AF+EF=FG+EF=EG=AB;
当点F在边AC上,延长FE、AD相交于点H,如图:
∵AD是△ABC的角平分线,
∴∠BAD=∠CAD,
∵EF∥AB,
∴∠BAD=∠H,∠B=∠DEH,
∴∠CAD=∠H,
∴FA=FH,
在△ABD和△HED中,,
∴△ABD≌△HED(AAS),
∴AB=EH,
∴AF-EF=FH-EF=EH=AB;
当点F在边AC的延长线上,AD是△ABC的外角平分线时,如图:
延长AD交EF于点I,
∵AD是△ABC的外角平分线,
∴∠JAD=∠CAD,
∵EF∥AB,
∴∠JAD=∠AIF,∠B=∠E,
∴∠CAD=∠AIF,
∴FA=FI,
在△ABD和△IED中,,
∴△ABD≌△IED(SAS),
∴AB=EI,
∴EF- AF= EF-IF=EI=AB.
【知识点】三角形全等的判定
28.【答案】(1)证明:如图,过点E作PQ∥CD,
,
,
,即
,
;
(2)解:如图,分别过E、K作EP∥CD、QK∥AB,
,
,
设,则,
设,则,
,
,,
,
,
,即,
,
;
(3)解:如图,连接FG,
,
,
即,
过G作GI⊥MN于I
,
,
设,
则,
,
,
,
,
,
,
.
【知识点】平行公理及推论;平行线的判定与性质;三角形的面积;角平分线的概念
21世纪教育网(www.21cnjy.com)
2 / 13
北师大版数学(2024)七年级下册全册综合题(精华)
一、单选题
1.下列说法正确的是( )
A.三条线段首尾顺次相接所组成的图形叫做三角形
B.三角形按边分类可分为三边都不相等的三角形、等腰三角形和等边三角形
C.关于轴对称的两个图形大小不变,形状改变
D.两角和一边对应相等的两个三角形全等
2.如图,直线,被直线所截,下列条件不能证明直线的是( )
A. B. C. D.
3.如图,D是的边上一点,将折叠,使点C落在上的点处,展开后得到折痕,则是的( )
A.中线 B.高线 C.角平分线 D.中位线
4.若,则( )
A. B. C. D.
5.下列交通标志中,是轴对称图形的是( )
A. B.
C. D.
6.下列语句中:
①经过一点有且只有一条直线与已知直线垂直;②过一点有且只有一条直线与已知直线平行;③互为邻补角的两个角的平分线互相垂直;④有公共顶点且相等的角是对顶角,其中错误的个数有( )
A.1个 B.2个 C.3个 D.4个
7.在平面内,将一个直角三角板按如图所示摆放在一组平行线上,若,则的度数是( )
A.35° B.40° C.45° D.50°
8.PM2.5是指大气中直径小于或等于0.000 002 5米的颗粒物,将0.000 002 5用科学记数法表示为( )
A.0.25×10-5 B.2.5×10-6 C.2.5×10-7 D.2.5×10-5
9.在△ABC中,∠BAC=115°,DE、FG分别为AB、AC的垂直平分线,则∠EAG的度数为( )
A.50° B.40° C.30° D.25°
10.在快速计算法中,法国的“小九九”从“一一得一”到“五五二十五”和我国的“小九九”算法是完全一样的,而后面“六到九”的运算就改用手势了.如计算8×9 时,左手伸出3根手指,右手伸出4根手指,两只手伸出手指数的和为7,未伸出手指数的积为2,则8×9=10×7+2=72.那么在计算6×8时,左、右手伸出的手指数应该分别为( )
A.1,3; B.3,1; C.1,4; D.4,1;
二、填空题
11.如图,现给出下列条件∶①,②,③,④.能够得到的条件是(填序号) .
12.已知,计算: .
13.若,则的值是 .
14.某商场为了增加销售额,推出“七月销售大酬宾”活动,其活动内容为:“凡七月份在该商场一次性购物超过100元以上者,超过100元的部分按8.5折优惠.”在大酬宾活动中,小王到该商场为单位购买单价为60元的办公用品x件,则应付货款y(元)与商品件数x的关系式是 .
15.如果关于x的整式和相乘的结果中不包含三次项,那么 .
16.如图,,平分,,.则的度数是 .
17.如图,矩形中,E是的中点,将沿折叠后得到,延长交于点F,若,,则的长为 .
18.如图,四边形ABCD是矩形纸片,AB=2.对折矩形纸片ABCD,使AD与BC重合,折痕为EF;展平后再过点B折叠矩形纸片,使点A落在EF上的点N,折痕BM与EF相交于点Q;再次展平,连接BN,MN,延长MN交BC于点G.有如下结论:
①∠ABN=60°;②AM=1;③QN= ;④△BMG是等边三角形;⑤P为线段BM上一动点,H是BN的中点,则PN+PH的最小值是 .
其中正确结论的序号是 .
三、解答题
19.如图,,分别是的中线和角平分线,.
(1)若的面积是20,且,求的长.
(2)若,求的度数.
20.如图,平分,平分,,,求的度数.
21.推理填空:
如图,
已知∠1=∠2,∠B=∠C,可推得AB∥CD.理由如下:
∵∠1=∠2(已知),且∠1=∠4( ▲ )
∴∠2=∠4 (等量代换)
∴CE∥BF ( )
∴∠▲ =∠3( )
又∵∠B=∠C(已知),∴∠3=∠B(等量代换)
∴AB∥CD ( )
22.对于任何数,我们规定:例如:.
(1)按照这个规定,请你化简;
(2)按照这个规定,请你计算:当时,求的值.
23.如图,已知 , , , ,求 的度数.
24.如图,直线AB,CD相交于点O,∠AOC=80°,∠1=30°,求∠2的度数.
25.如图,在四边形中,,,延长至点E,平分,交于点G,求的度数.
26.如图,直线AB∥CD,BC平分∠ABD,∠1=65°,求∠2的度数.
27.已知:AD是△ABC的角平分线,点E为直线BC上一点,BD=DE,过点E作EF∥AB交直线AC于点F,当点F在边AC的延长线上时,如图①易证AF+EF=AB;当点F在边AC上,如图②;当点F在边AC的延长线上,AD是△ABC的外角平分线时,如图3.写出AF、EF与AB的数量关系,并对图②进行证明.
28. 已知:点F、点G分别为直线上的点,E为平面内任意一点,连接与直交于点M,.
(1)如图1,求证:;
(2)如图2,和分别平分与,和的反向延长线交于点K,探究和的数量关系,并证明你的结论;
(3)如图3,在(2)的条件下,与交于点N,射线交直线于P,若,求的长.
答案解析部分
1.【答案】D
【知识点】轴对称的性质;三角形相关概念
2.【答案】B
【知识点】平行线的判定;对顶角及其性质
3.【答案】B
【知识点】三角形的角平分线、中线和高;翻折变换(折叠问题)
4.【答案】B
【知识点】多项式除以单项式
5.【答案】D
【知识点】轴对称图形
6.【答案】C
【知识点】垂线的概念;平行公理及推论;对顶角及其性质;邻补角
7.【答案】A
【知识点】平行线的性质
8.【答案】B
【知识点】科学记数法表示大于0且小于1的数
9.【答案】A
【知识点】线段垂直平分线的性质
10.【答案】A
【知识点】有理数的加减乘除混合运算的法则;定义新运算
11.【答案】②③④
【知识点】平行线的判定
12.【答案】5
【知识点】平方差公式及应用
13.【答案】108
【知识点】同底数幂的乘法;幂的乘方运算
14.【答案】
【知识点】用关系式表示变量间的关系
15.【答案】2
【知识点】多项式乘多项式
16.【答案】
【知识点】平行线的性质;角平分线的性质
17.【答案】5
【知识点】直角三角形全等的判定-HL;矩形的性质
18.【答案】①④⑤
【知识点】轴对称的应用-最短距离问题
19.【答案】(1)10
(2)
【知识点】等腰三角形的性质
20.【答案】
【知识点】角的运算;角平分线的性质
21.【答案】解:∵∠1=∠2(已知),且∠1=∠4(对顶角相等),
∴∠2=∠4 (等量代换),
∴CE∥BF (同位角相等,两直线平行),
∴∠C=∠3(两直线平行,同位角相等);
又∵∠B=∠C(已知),
∴∠3=∠B(等量代换),
∴AB∥CD (内错角相等,两直线平行).
【知识点】平行线的判定与性质
22.【答案】(1)由题意得:
(2)由题意得:
,
,
,
原式.
【知识点】多项式乘多项式
23.【答案】解:∵AD⊥BC,EF⊥BC,
∴AD∥EF,
∴∠1=∠BAD,
又∵∠1=∠2,
∴∠2=∠BAD,
∴AB∥DM,
∴∠AMD+∠BAC =180°,
∵ ,
∴∠AMD=180°-∠BAC=180°-70°=110°.
【知识点】平行线的判定与性质
24.【答案】解:∵∠AOC=∠BOD,∠AOC=80°,
∴∠BOD=80°,
∵∠1+∠2=∠BOD,∠1=30°,
∴∠2=∠BOD-∠1=50°.
【知识点】对顶角及其性质
25.【答案】
【知识点】平行线的判定与性质;角平分线的性质
26.【答案】解: ∵AB∥CD,
∴∠1=∠CBA=65°,∠2=∠DBE,
又∵BC平分∠ABD,
∴∠ABD=2∠ABC=130°,
∴∠DBE=180°-∠ABD=180°-130°=50°,
∴∠2=50°.
【知识点】平行线的性质
27.【答案】解:当点F在边AC的延长线上时,延长EF、AD相交于点G,如图:
∵AD是△ABC的角平分线,
∴∠BAD=∠CAD,
∵EF∥AB,
∴∠BAD=∠G,∠B=∠E,
∴∠CAD=∠G,
∴FA=FG,
在△ABD和△GED中,,
∴△ABD≌△GED(AAS),
∴AB=EG,
∴AF+EF=FG+EF=EG=AB;
当点F在边AC上,延长FE、AD相交于点H,如图:
∵AD是△ABC的角平分线,
∴∠BAD=∠CAD,
∵EF∥AB,
∴∠BAD=∠H,∠B=∠DEH,
∴∠CAD=∠H,
∴FA=FH,
在△ABD和△HED中,,
∴△ABD≌△HED(AAS),
∴AB=EH,
∴AF-EF=FH-EF=EH=AB;
当点F在边AC的延长线上,AD是△ABC的外角平分线时,如图:
延长AD交EF于点I,
∵AD是△ABC的外角平分线,
∴∠JAD=∠CAD,
∵EF∥AB,
∴∠JAD=∠AIF,∠B=∠E,
∴∠CAD=∠AIF,
∴FA=FI,
在△ABD和△IED中,,
∴△ABD≌△IED(SAS),
∴AB=EI,
∴EF- AF= EF-IF=EI=AB.
【知识点】三角形全等的判定
28.【答案】(1)证明:如图,过点E作PQ∥CD,
,
,
,即
,
;
(2)解:如图,分别过E、K作EP∥CD、QK∥AB,
,
,
设,则,
设,则,
,
,,
,
,
,即,
,
;
(3)解:如图,连接FG,
,
,
即,
过G作GI⊥MN于I
,
,
设,
则,
,
,
,
,
,
,
.
【知识点】平行公理及推论;平行线的判定与性质;三角形的面积;角平分线的概念
21世纪教育网(www.21cnjy.com)
2 / 13
同课章节目录
