2025年中考数学复习--动点在二次函数中的综合(1) 提升训练 (含解析)
文档属性
| 名称 | 2025年中考数学复习--动点在二次函数中的综合(1) 提升训练 (含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 567.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-08 06:55:19 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
动点在二次函数中的综合(1)
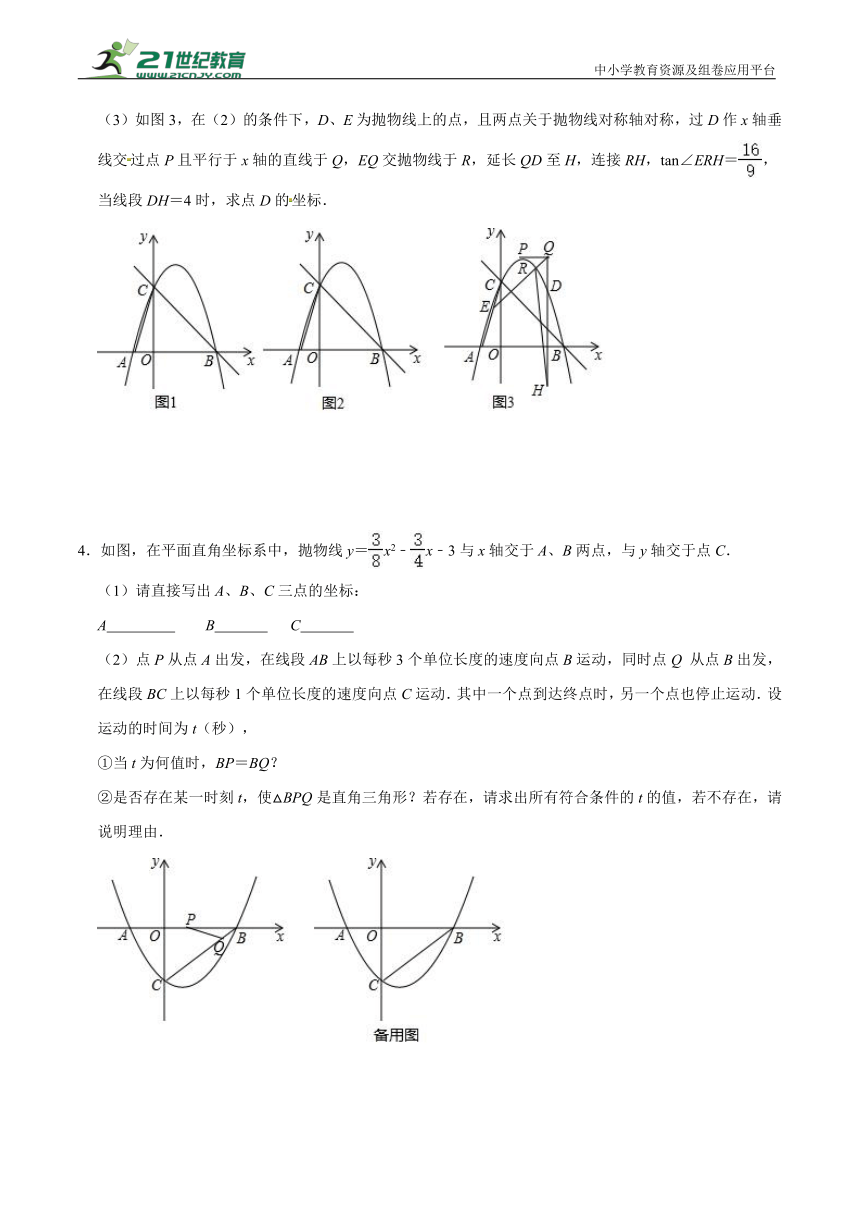
1.如图,抛物线y=ax2+bx+6与x轴交于点A(﹣2,0),B(6,0),与y轴交于点C.
(1)求该抛物线的函数解析式;
(2)点D(4,m)在抛物线上,连接BC、BD.试问,在对称轴左侧的抛物线上是否存在一点P,满足∠PBC=∠DBC?如果存在,请求出P点的坐标;如果不存在,请说明理由.
2.如图,在平面直角坐标系中,直线y=x+1与抛物线y=x2+bx+c交于A,B(4,5)两点,点A在x轴上.
(1)求抛物线的解析式;
(2)点E是线段AB上一动点(点A,B除外),过点E作x轴的垂线交抛物线于点F,当线段EF的长度最大时,求点E的坐标;
(3)在(2)的条件下,抛物线上是否存在一点P,使∠PEF=90°?若存在,求出点P的坐标;若不存在,说明理由.
3.如图,在平面直角坐标系中,点O为坐标原点,抛物线y=a(x+1)(x﹣3)交x轴于A、B两点,交y轴于点C,∠ABC=45°,
(1)求抛物线的解析式;
(2)如图2,P为第一象限内抛物线上一点,△BCP的面积为3时,且∠BCP>45°,求P点坐标;
(3)如图3,在(2)的条件下,D、E为抛物线上的点,且两点关于抛物线对称轴对称,过D作x轴垂线交过点P且平行于x轴的直线于Q,EQ交抛物线于R,延长QD至H,连接RH,tan∠ERH=,当线段DH=4时,求点D的坐标.
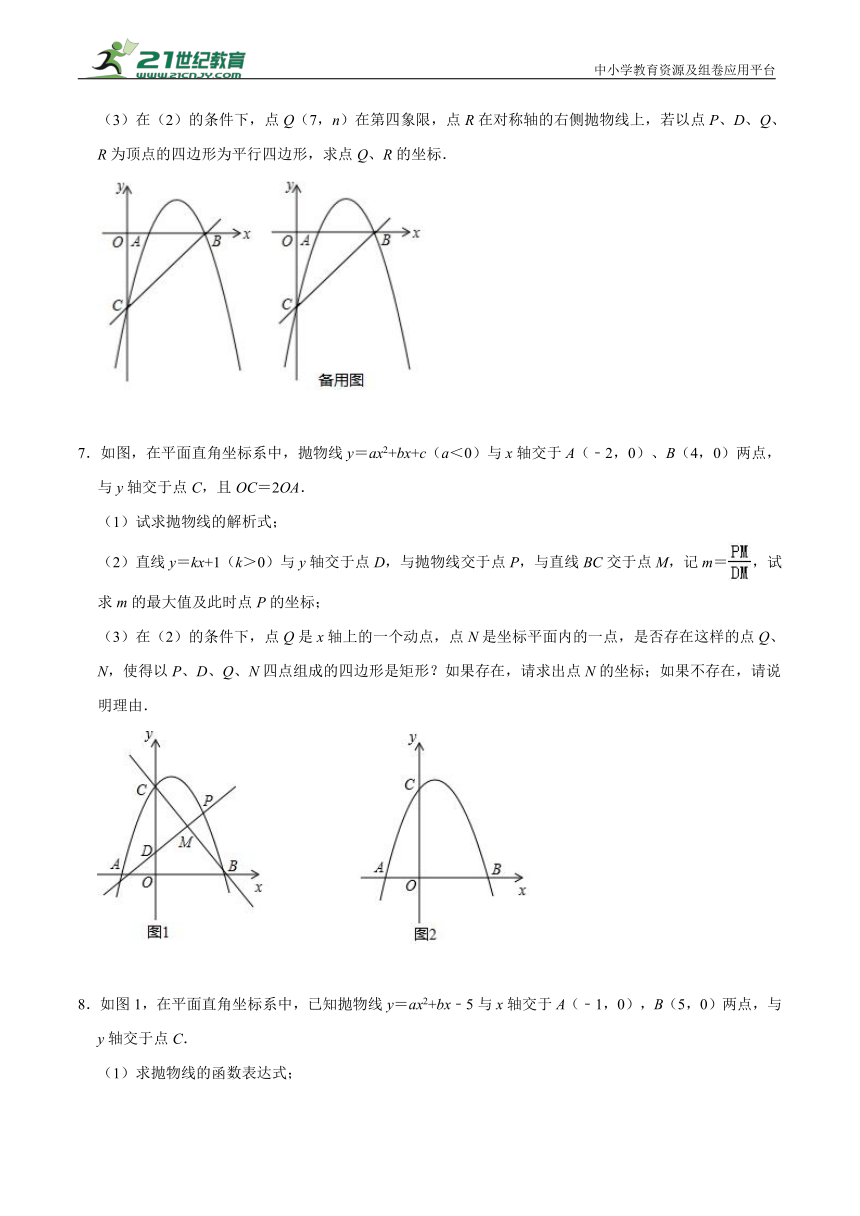
4.如图,在平面直角坐标系中,抛物线y=x2﹣x﹣3与x轴交于A、B两点,与y轴交于点C.
(1)请直接写出A、B、C三点的坐标:
A B C
(2)点P从点A出发,在线段AB上以每秒3个单位长度的速度向点B运动,同时点Q 从点B出发,在线段BC上以每秒1个单位长度的速度向点C运动.其中一个点到达终点时,另一个点也停止运动.设运动的时间为t(秒),
①当t为何值时,BP=BQ?
②是否存在某一时刻t,使△BPQ是直角三角形?若存在,请求出所有符合条件的t的值,若不存在,请说明理由.
5.如图,在平面直角坐标系xOy中,一次函数y=x+m(m为常数)的图象与x轴交于点A(﹣3,0),与y轴交于点C,以直线x=1为对称轴的抛物线y=ax2+bx+c(a、b、c为常数,且a≠0)经过A、C两点,并与x轴的正半轴交于点B
(1)求m的值及抛物线的函数表达式;
(2)是否存在抛物线上一动点Q,使得△ACQ是以AC为直角边的直角三角形?若存在,求出点Q的横坐标;若存在,请说明理由;
(3)若P是抛物线对称轴上一动点,且使△ACP周长最小,过点P任意作一条与y轴不平行的直线交抛物线于M1(x1,y1),M2(x2,y2)两点,试问是否为定值,如果是,请求出结果,如果不是请说明理由.
(参考公式:在平面直角坐标之中,若A(x1,y1),B(x2,y2),则A,B两点间的距离为AB=)
6.如图,在平面直角坐标系中,直线y=kx﹣7与y轴交于点C,与x轴交于点B,抛物线y=ax2+bx+14a经过B、C两点,与x轴的正半轴交于另一点A,且OA:OC=2:7.
(1)求抛物线的解析式;
(2)点D在线段CB上,点P在对称轴的左侧抛物线上,PD=PB,当tan∠PDB=2,求点P的坐标;
(3)在(2)的条件下,点Q(7,n)在第四象限,点R在对称轴的右侧抛物线上,若以点P、D、Q、R为顶点的四边形为平行四边形,求点Q、R的坐标.
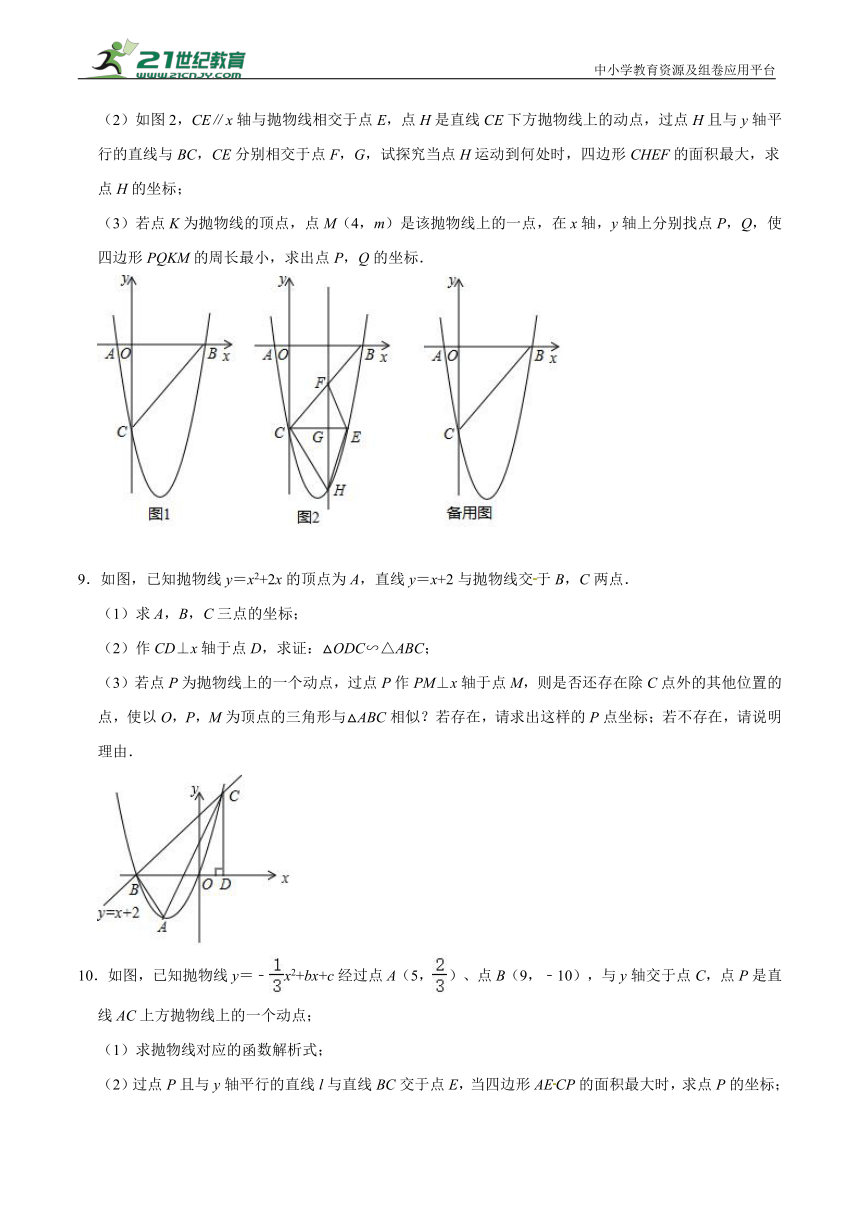
7.如图,在平面直角坐标系中,抛物线y=ax2+bx+c(a<0)与x轴交于A(﹣2,0)、B(4,0)两点,与y轴交于点C,且OC=2OA.
(1)试求抛物线的解析式;
(2)直线y=kx+1(k>0)与y轴交于点D,与抛物线交于点P,与直线BC交于点M,记m=,试求m的最大值及此时点P的坐标;
(3)在(2)的条件下,点Q是x轴上的一个动点,点N是坐标平面内的一点,是否存在这样的点Q、N,使得以P、D、Q、N四点组成的四边形是矩形?如果存在,请求出点N的坐标;如果不存在,请说明理由.
8.如图1,在平面直角坐标系中,已知抛物线y=ax2+bx﹣5与x轴交于A(﹣1,0),B(5,0)两点,与y轴交于点C.
(1)求抛物线的函数表达式;
(2)如图2,CE∥x轴与抛物线相交于点E,点H是直线CE下方抛物线上的动点,过点H且与y轴平行的直线与BC,CE分别相交于点F,G,试探究当点H运动到何处时,四边形CHEF的面积最大,求点H的坐标;
(3)若点K为抛物线的顶点,点M(4,m)是该抛物线上的一点,在x轴,y轴上分别找点P,Q,使四边形PQKM的周长最小,求出点P,Q的坐标.
9.如图,已知抛物线y=x2+2x的顶点为A,直线y=x+2与抛物线交于B,C两点.
(1)求A,B,C三点的坐标;
(2)作CD⊥x轴于点D,求证:△ODC∽△ABC;
(3)若点P为抛物线上的一个动点,过点P作PM⊥x轴于点M,则是否还存在除C点外的其他位置的点,使以O,P,M为顶点的三角形与△ABC相似?若存在,请求出这样的P点坐标;若不存在,请说明理由.
10.如图,已知抛物线y=﹣x2+bx+c经过点A(5,)、点B(9,﹣10),与y轴交于点C,点P是直线AC上方抛物线上的一个动点;
(1)求抛物线对应的函数解析式;
(2)过点P且与y轴平行的直线l与直线BC交于点E,当四边形AECP的面积最大时,求点P的坐标;
(3)当∠PCB=90°时,作∠PCB的角平分线,交抛物线于点F.
①求点P和点F的坐标;
②在直线CF上是否存在点Q,使得以F、P、Q为顶点的三角形与△BCF相似,若存在,求出点Q的坐标;若不存在,请说明理由.
1.解:(1)当x=0时,y=6,
∴点C的坐标为(0,6).
设抛物线的解析式为y=a(x+2)(x﹣6),将C(0,6)代入得:﹣12a=6,解得a=﹣.
∴抛物线的解析式为y=﹣(x+2)(x﹣6),整理得:y=﹣x2+2x+6.
(2)将x=4代入得:y=6.
∴D(4,6).
如图所示:作点DE∥x轴,过点B作BE∥y轴,作点D关于BC的对称点D′,则BD=BD′,过点D′作D′F⊥x轴,垂足为F.
∵B(6,0),C(0,6),
∴OB=OC.
∴∠OBC=45°.
∴∠OBC=∠EBC.
又∵∠D′BC=∠DBC,
∴∠DBE=∠D′BF.
在△DEB和△D′FB中,,
∴△DEB≌△D′FB.
∴D′F=ED=2,BF=BE=6.
∴点D′的坐标为(0,2).
设BD′的解析式为y=kx+2,将点B的坐标代入得:6k+2=0,解得k=﹣,
∴BD′的解析式为y=﹣x+2.
将y=﹣x+2代入y=﹣x2+2x+6得:﹣x+2=﹣x2+2x+6,整理得:3x2﹣14x﹣24=0,解得:x=6(舍去)或x=﹣.
将x=﹣代入得:y=﹣×(﹣)+2=+2=
∴点P的坐标为(﹣,).
2.解:(1)把y=0代入y=x+1得:x+1=0,解得:x=﹣1,
∴点A(﹣1,0).
将点A和点B的坐标代入抛物线的解析式得:,解得:b=﹣2,c=﹣3.
∴抛物线的解析式为y=x2﹣2x﹣3.
(2)如图1所示:
设点E的坐标为(x,x+1),则点F的坐标为F(x,x2﹣2x﹣3).
设EF=(x+1)﹣(x2﹣2x﹣3)=﹣x2+3x+4=﹣(x﹣)2+.
∴当x=时,EF有最大值.
将x=代入y=x+1得:y=.
∴E(,).
(3)如图2所示:过点E作PE⊥EF,交抛物线与点P或点P′,则yp=.
将y=代入抛物线的解析式得:x2﹣2x﹣3=,解得:x=1+,x=1﹣.
∴点P的坐标为(1﹣,)或(1+,).
3.解:(1)对于抛物线y=a(x+1)(x﹣3),令y=0,得到a(x+1)(x﹣3)=0,解得x=﹣1或3,
∴A(﹣1,0),B(3,0),
∴OB=3,
∵∠ABC=45°,
∴OC=OB=3,
∴C(0,3),把(0,3)代入y=a(x+1)(x﹣3)得到a=﹣1,
∴抛物线的解析式为y=﹣x2+2x+3.
(2)如图2中,作PH⊥AB于H,交BC于T.,作CE⊥PH于E,设P(m,﹣m2+2m+3).
∵B(3,0),C(0,3),
∴直线BC的解析式为y=﹣x+3,
∴T(m,﹣m+3),
∵S△PBC=S△PTC+S△PTB= PT CE+ PT BH=PT (CE+BH)= PT OB=×(﹣m2+3m)×3=3,
整理得m2﹣3m+2=0,
∴m=1或2,
∵∠PCB>45°,
∴m=1,
∴P(1,4).
(3)如图3中,作RM⊥DQ于M,连接EM.DH交AB于N.设D(n,﹣n2+2n+3).
∵PQ∥DE,PQ⊥DQ,DH⊥AB,
∴Q(n,4),
∴DE=2(n﹣1),DQ=4﹣(﹣n2+2n+3)=(n﹣1)2,
∴==,==,
∴=,
∵∠EDQ=∠EDH=90°,
∴△EDQ∽△HDE,
∴∠DEQ=∠EHD,
∵∠DEQ+∠EQD=90°,
∴∠EHD+∠EQD=90°,
∴∠HEQ=90°,
∵∠REH+∠RMH=180°,
∴E、H、M、R四点共圆,
∴∠ERH=∠EMH,
∴tan∠ERH=tan∠EMD==,
∴DM=(n﹣1),
∴QM=(n﹣1)2﹣(n﹣1),
∵RM∥DE,
∴=,
∴RM=2n﹣,
∴R[﹣n+,4﹣(n﹣1)2+(n﹣1)],
把点R坐标代入y=﹣x2+2x+3得到,4﹣(n﹣1)2+(n﹣1)=﹣(﹣n+)2+2(﹣n+)+3,
解得n=,
∴D(,).
4.解:(1)由y=x2﹣x﹣3得到:y=(x﹣4)(x﹣2)或y=(x﹣1)2﹣,
所以 A(﹣2,0),B(4,0),
令x=0,则y=﹣3,
所以 C(0,﹣3);
综上所述,A(﹣2,0),B(4,0),C(0,﹣3);
故答案是:(﹣2,0),(4,0),(0,﹣3);
(2)①∵A(﹣2,0),B(4,0),
∴AB=6,
由BP=BQ得到:6﹣3t=t,
解得t=;
②∵B(4,0),C(0,﹣3),
∴OB=4,OC=3,
∴BC==5.
i)如图1,当∠BPQ=90°时,△BPQ∽△BOC,则=,即=,
解得t=;
ii)如图2,当∠BQP=90°时,△BPQ∽△BCO,则=,即=,
解得t=
综上所述,t的值是:或.
5.解:(1)∵一次函数y=x+m(m为常数)的图象与x轴交于点A(﹣3,0),
∴0=×(﹣3)+m,解得m=,
∴一次函数解析式为y=x+,
∴C点坐标为(0,).
∵以直线x=1为对称轴的抛物线y=ax2+bx+c(a、b、c为常数,且a≠0)经过A(﹣3,0)、C(0,),
∴,解得,
∴抛物线的函数表达式为y=﹣x2+x+;
(2)存在.设Q(x,﹣x2+x+).
①当点C为直角顶点时,如图,作CQ⊥AC交抛物线于点Q,QE⊥y轴于E.
在△ACO与△CQE中,
,
∴△ACO∽△CQE,
∴=,即=,
解得x1=5.2,x2=0(不合题意舍去);
②当点A为直角顶点时,如图,作AQ′⊥AC交抛物线于点Q′,Q′E′⊥x轴于E.
在△ACO与△Q′AE′中,
,
∴△ACO∽△Q′AE′,
∴=,即=,
解得x1=8.2,x2=﹣3(不合题意舍去).
综上所述:Q点的横坐标为5.2或8.2;
(3)∵y=﹣x2+x+与x轴交于A(﹣3,0)、B两点,对称轴为直线x=1,
∴B点坐标为(5,0),
∵C(0,),
∴直线BC的解析式为y=﹣x+,
当x=1时,y=﹣×1+=3,
∴P(1,3).
设过点P的直线为:y=kx+3﹣k,
把y=kx+3﹣k代入y=﹣x2+x+,
得kx+3﹣k=﹣x2+x+,
整理得,x2+(4k﹣2)x﹣4k﹣3=0,
∴x1+x2=2﹣4k,x1x2=﹣4k﹣3,y1﹣y2=k(x1﹣x2),
∴(x1﹣x2)2=(x1+x2)2﹣4x1x2=(2﹣4k)2﹣4(﹣4k﹣3)=16k2+16,
∴M1M2===4(1+k2),
同理:M1P==,
M2P=,
∴M1P M2P= =|(x1﹣1)(x2﹣1)| (1+k2)=4(1+k2),
∴=1为定值.
6.解:(1)∵直线y=kx﹣7与y轴的负半轴交于点C
∴C(0,﹣7),
∴OC=7,
∵抛物线y=ax2+bx+14a经过点C,
∴14a=﹣7,
∴a=﹣,
∴y=﹣x2+bx﹣7,
∵OA:OC=2:7.
∴OA=2,
∴A(2,0)
∵抛物线y=﹣x2+bx﹣7经过点A,
∴b=
∴抛物线的解析式为y=﹣x2+x﹣7,
(2)如图1,
∵抛物线y=﹣x2+x﹣7经过B点,
令y=0解得x=7或x=2(舍去),
∴B(7,0),
∴OB=7,
∴OC=OB,
∴∠OCB=∠OBC=45°
过点P作PF⊥x轴于点G,交CB延长线于点F,则PF∥y轴,
∴∠CFG=∠OCB=45°,
∴BF=GF,
过P作PE⊥BC于点E,
∵PD=PB,
∴∠PBD=∠PDB,
∴tan∠PBD=tan∠PDB=2,
∴PE=2BE,
∵EF=PE,
∴BF=BE,
∴PF=PE=2 BE=2 BF=4GF,
∴PG=3GF,
∵直线y=kx﹣7过B点,
∴k=1,
∴y=x﹣7,
设F(m,m﹣7),则P(m,﹣3(m﹣7)),
∵点P在抛物线y=﹣x2+x﹣7上,
∴﹣3(m﹣7)=﹣m2+m﹣7,
解得m=7(舍去)或m=8,
∴P(8,﹣3);
(3)如图2,当DP∥QR时,即四边形DQRP是平行四边形,
∵B(7,0),Q(7,m)
∴BQ∥y轴
过P作PN∥BQ,过D作DN⊥BQ交PN于点N,
过R作RM⊥BQ于点M.
设PD交BQ于点T,DN交BM于点I,
∴∠DTB=∠DPN,∠PTQ=∠RQM,
∵∠DTB=∠PTQ,
∴∠DPN=∠RQM,
∵四边形DPRQ是平行四边形,
∴DP=RQ,
在△RMQ和△DNP中,
,
∴△RMQ≌△DNP(AAS),
∴RM=DN,MQ=PN,
由(2)可求F(8,1),GF=1,BD=2BE=2BF=2 GF=2 ,
∵∠QBC=45°,∴BI=DI=2,
∴D(5,﹣2),
设R点的横坐标为t,
∵RM=DN,
∴t﹣7=8﹣5,
解得t=10,
∵点R在抛物线y=﹣x2+x﹣7 上,
∴当t=10时,﹣×102+×10﹣7=﹣12,
∴R(10,﹣12),
∵MQ=PN,
∴3﹣2=﹣12﹣n,
∴n=﹣11,
∴R(10,﹣12),Q(7,﹣11),
如图3,当DR∥QP时,即四边形DQPR是平行四边形
同理可求得R(6,2),Q(7,﹣7).
7.解:(1)因为抛物线y=ax2+bx+c经过A(﹣2,0)、B(4,0)两点,
所以可以假设y=a(x+2)(x﹣4),
∵OC=2OA,OA=2,
∴C(0,4),代入抛物线的解析式得到a=﹣,
∴y=﹣(x+2)(x﹣4)或y=﹣x2+x+4或y=﹣(x﹣1)2+.
(2)如图1中,由题意,点P在y轴的右侧,作PE⊥x轴于E,交BC于F.
∵CD∥PE,
∴△CMD∽△FMP,
∴m==,
∵直线y=kx+1(k>0)与y轴交于点D,则D(0,1),
∵BC的解析式为y=﹣x+4,
设P(n,﹣n2+n+4),则F(n,﹣n+4),
∴PF=﹣n2+n+4﹣(﹣n+4)=﹣(n﹣2)2+2,
∴m==﹣(n﹣2)2+,
∵﹣<0,
∴当n=2时,m有最大值,最大值为,此时P(2,4).
(3)存在这样的点Q、N,使得以P、D、Q、N四点组成的四边形是矩形.
①当DP是矩形的边时,有两种情形,
如图2﹣1中,四边形DQNP是矩形时,
有(2)可知P(2,4),代入y=kx+1中,得到k=,
∴直线DP的解析式为y=x+1,可得D(0,1),E(﹣,0),
由△DOE∽△QOD可得=,
∴OD2=OE OQ,
∴1= OQ,
∴OQ=,
∴Q(,0).
根据矩形的性质,将点P向右平移个单位,向下平移1个单位得到点N,
∴N(2+,4﹣1),即N(,3)
b、如图2﹣2中,四边形PDNQ是矩形时,
∵直线PD的解析式为y=x+1,PQ⊥PD,
∴直线PQ的解析式为y=﹣x+,
∴Q(8,0),
根据矩形的性质可知,将点D向右平移6个单位,向下平移4个单位得到点N,
∴N(0+6,1﹣4),即N(6,﹣3).
②当DP是对角线时,设Q(x,0),则QD2=x2+1,QP2=(x﹣2)2+42,PD2=13,
∵Q是直角顶点,
∴QD2+QP2=PD2,
∴x2+1+(x﹣2)2+16=13,
整理得x2﹣2x+4=0,方程无解,此种情形不存在,
综上所述,满足条件的点N坐标为(,3)或(6,﹣3).
8.解:(1)∵点A(﹣1,0),B(5,0)在抛物线y=ax2+bx﹣5上,
∴,
解得,
∴抛物线的表达式为y=x2﹣4x﹣5,
(2)设H(t,t2﹣4t﹣5),
∵CE∥x轴,
∴点E的纵坐标为﹣5,
∵E在抛物线上,
∴x2﹣4x﹣5=﹣5,
∴x=0(舍)或x=4,
∴E(4,﹣5),
∴CE=4,
∵B(5,0),C(0,﹣5),
∴直线BC的解析式为y=x﹣5,
∴F(t,t﹣5),
∴HF=t﹣5﹣(t2﹣4t﹣5)=﹣(t﹣)2+,
∵CE∥x轴,HF∥y轴,
∴CE⊥HF,
∴S四边形CHEF=CE HF=﹣2(t﹣)2+,
∴H(,﹣);
(3)如图2,∵K为抛物线的顶点,
∴K(2,﹣9),
∴K关于y轴的对称点K'(﹣2,﹣9),
∵M(4,m)在抛物线上,
∴M(4,﹣5),
∴点M关于x轴的对称点M'(4,5),
∴直线K'M'的解析式为y=x﹣,
∴P(,0),Q(0,﹣).
9.(1)解:y=x2+2x=(x+1)2﹣1,
∴顶点A(﹣1,﹣1);
由,解得:或
∴B(﹣2,0),C(1,3);
(2)证明:∵A(﹣1,﹣1),B(﹣2,0),C(1,3),
∴AB==,
BC==3,
AC==2,
∴AB2+BC2=AC2,==,
∴∠ABC=90°,
∵OD=1,CD=3,
∴=,
∴,∠ABC=∠ODC=90°,
∴△ODC∽△ABC;
(3)存在这样的P点,
设M(x,0),则P(x,x2+2x),
∴OM=|x|,PM=|x2+2x|,
当以O,P,M为顶点的三角形与△ABC相似时,
有=或=,
由(2)知:AB=,CB=3,
①当=时,则=,
当P在第二象限时,x<0,x2+2x>0,
∴,解得:x1=0(舍),x2=﹣,
当P在第三象限时,x<0,x2+2x<0,
∴=,解得:x1=0(舍),x2=﹣,
②当=时,则=3,
同理代入可得:x=﹣5或x=1(舍),
综上所述,存在这样的点P,坐标为(﹣,﹣)或(﹣,)或(﹣5,15).
10.解:(1)∵抛物线y=﹣x2+bx+c经过点A(5,)、点B(9,﹣10),
∴,
解得,
∴抛物线对应的函数表达式为y=﹣x2+2x﹣1;
(2)由抛物线可得,C(0,﹣1),B(9,﹣10),
∴直线BC为:y=﹣x﹣1,
设点P的坐标为(m,﹣m2+2m﹣1),则E(m,﹣m﹣1),
∴PE=﹣m2+2m﹣1﹣(﹣m﹣1)=﹣m2+3m,
∴四边形AECP的面积=△APE面积+△CPE面积
=×(﹣m2+3m)×m+×(﹣m2+3m)×(5﹣m)
=(﹣m2+3m)
=﹣m2+m,
=﹣(m﹣)2+,
∴当m=时,﹣m2+2m﹣1=,
∴点P坐标为( ,);
(3)①过点B作BH⊥y轴于H,
∵C(0,﹣1),B(9,﹣10),
∴CH=BH=9,
∴∠BCH=45°,
∵∠PCB=90°,CF平分∠PCB,
∴∠BCF=45°,
∴∠FCH=90°,即CF∥x轴,
当y=﹣1时,﹣1=﹣x2+2x﹣1,
解得x1=0,x2=6,
∴F(6,﹣1),
∵CP⊥CB,C(0,﹣1),
∴直线CP为:y=x﹣1,
当x﹣1=﹣x2+2x﹣1时,解得x1=0,x2=3,
当x=3时,y=2,
∴P(3,2);
②∵直线CB:y=﹣x﹣1,直线PF:y=﹣x+5,
∴CB∥PF,
∴∠BCF=∠PFC=45°,
∴在直线CF上存在满足条件的点Q,
设Q(t,﹣1),
由题可得CF=6,CB=9,PF=3,
(ⅰ)如图所示,当△PFQ1∽△BCF时,
=,即=,
解得t=4,
∴Q1(4,﹣1);
(ⅱ)如图所示,当△PFQ∽△FCB时,
=,即=,
解得t=﹣3,
∴Q2(﹣3,﹣1).
综上所述,点Q的坐标为(4,﹣1)或(﹣3,﹣1).
动点在二次函数中的综合(1)
1.如图,抛物线y=ax2+bx+6与x轴交于点A(﹣2,0),B(6,0),与y轴交于点C.
(1)求该抛物线的函数解析式;
(2)点D(4,m)在抛物线上,连接BC、BD.试问,在对称轴左侧的抛物线上是否存在一点P,满足∠PBC=∠DBC?如果存在,请求出P点的坐标;如果不存在,请说明理由.
2.如图,在平面直角坐标系中,直线y=x+1与抛物线y=x2+bx+c交于A,B(4,5)两点,点A在x轴上.
(1)求抛物线的解析式;
(2)点E是线段AB上一动点(点A,B除外),过点E作x轴的垂线交抛物线于点F,当线段EF的长度最大时,求点E的坐标;
(3)在(2)的条件下,抛物线上是否存在一点P,使∠PEF=90°?若存在,求出点P的坐标;若不存在,说明理由.
3.如图,在平面直角坐标系中,点O为坐标原点,抛物线y=a(x+1)(x﹣3)交x轴于A、B两点,交y轴于点C,∠ABC=45°,
(1)求抛物线的解析式;
(2)如图2,P为第一象限内抛物线上一点,△BCP的面积为3时,且∠BCP>45°,求P点坐标;
(3)如图3,在(2)的条件下,D、E为抛物线上的点,且两点关于抛物线对称轴对称,过D作x轴垂线交过点P且平行于x轴的直线于Q,EQ交抛物线于R,延长QD至H,连接RH,tan∠ERH=,当线段DH=4时,求点D的坐标.
4.如图,在平面直角坐标系中,抛物线y=x2﹣x﹣3与x轴交于A、B两点,与y轴交于点C.
(1)请直接写出A、B、C三点的坐标:
A B C
(2)点P从点A出发,在线段AB上以每秒3个单位长度的速度向点B运动,同时点Q 从点B出发,在线段BC上以每秒1个单位长度的速度向点C运动.其中一个点到达终点时,另一个点也停止运动.设运动的时间为t(秒),
①当t为何值时,BP=BQ?
②是否存在某一时刻t,使△BPQ是直角三角形?若存在,请求出所有符合条件的t的值,若不存在,请说明理由.
5.如图,在平面直角坐标系xOy中,一次函数y=x+m(m为常数)的图象与x轴交于点A(﹣3,0),与y轴交于点C,以直线x=1为对称轴的抛物线y=ax2+bx+c(a、b、c为常数,且a≠0)经过A、C两点,并与x轴的正半轴交于点B
(1)求m的值及抛物线的函数表达式;
(2)是否存在抛物线上一动点Q,使得△ACQ是以AC为直角边的直角三角形?若存在,求出点Q的横坐标;若存在,请说明理由;
(3)若P是抛物线对称轴上一动点,且使△ACP周长最小,过点P任意作一条与y轴不平行的直线交抛物线于M1(x1,y1),M2(x2,y2)两点,试问是否为定值,如果是,请求出结果,如果不是请说明理由.
(参考公式:在平面直角坐标之中,若A(x1,y1),B(x2,y2),则A,B两点间的距离为AB=)
6.如图,在平面直角坐标系中,直线y=kx﹣7与y轴交于点C,与x轴交于点B,抛物线y=ax2+bx+14a经过B、C两点,与x轴的正半轴交于另一点A,且OA:OC=2:7.
(1)求抛物线的解析式;
(2)点D在线段CB上,点P在对称轴的左侧抛物线上,PD=PB,当tan∠PDB=2,求点P的坐标;
(3)在(2)的条件下,点Q(7,n)在第四象限,点R在对称轴的右侧抛物线上,若以点P、D、Q、R为顶点的四边形为平行四边形,求点Q、R的坐标.
7.如图,在平面直角坐标系中,抛物线y=ax2+bx+c(a<0)与x轴交于A(﹣2,0)、B(4,0)两点,与y轴交于点C,且OC=2OA.
(1)试求抛物线的解析式;
(2)直线y=kx+1(k>0)与y轴交于点D,与抛物线交于点P,与直线BC交于点M,记m=,试求m的最大值及此时点P的坐标;
(3)在(2)的条件下,点Q是x轴上的一个动点,点N是坐标平面内的一点,是否存在这样的点Q、N,使得以P、D、Q、N四点组成的四边形是矩形?如果存在,请求出点N的坐标;如果不存在,请说明理由.
8.如图1,在平面直角坐标系中,已知抛物线y=ax2+bx﹣5与x轴交于A(﹣1,0),B(5,0)两点,与y轴交于点C.
(1)求抛物线的函数表达式;
(2)如图2,CE∥x轴与抛物线相交于点E,点H是直线CE下方抛物线上的动点,过点H且与y轴平行的直线与BC,CE分别相交于点F,G,试探究当点H运动到何处时,四边形CHEF的面积最大,求点H的坐标;
(3)若点K为抛物线的顶点,点M(4,m)是该抛物线上的一点,在x轴,y轴上分别找点P,Q,使四边形PQKM的周长最小,求出点P,Q的坐标.
9.如图,已知抛物线y=x2+2x的顶点为A,直线y=x+2与抛物线交于B,C两点.
(1)求A,B,C三点的坐标;
(2)作CD⊥x轴于点D,求证:△ODC∽△ABC;
(3)若点P为抛物线上的一个动点,过点P作PM⊥x轴于点M,则是否还存在除C点外的其他位置的点,使以O,P,M为顶点的三角形与△ABC相似?若存在,请求出这样的P点坐标;若不存在,请说明理由.
10.如图,已知抛物线y=﹣x2+bx+c经过点A(5,)、点B(9,﹣10),与y轴交于点C,点P是直线AC上方抛物线上的一个动点;
(1)求抛物线对应的函数解析式;
(2)过点P且与y轴平行的直线l与直线BC交于点E,当四边形AECP的面积最大时,求点P的坐标;
(3)当∠PCB=90°时,作∠PCB的角平分线,交抛物线于点F.
①求点P和点F的坐标;
②在直线CF上是否存在点Q,使得以F、P、Q为顶点的三角形与△BCF相似,若存在,求出点Q的坐标;若不存在,请说明理由.
1.解:(1)当x=0时,y=6,
∴点C的坐标为(0,6).
设抛物线的解析式为y=a(x+2)(x﹣6),将C(0,6)代入得:﹣12a=6,解得a=﹣.
∴抛物线的解析式为y=﹣(x+2)(x﹣6),整理得:y=﹣x2+2x+6.
(2)将x=4代入得:y=6.
∴D(4,6).
如图所示:作点DE∥x轴,过点B作BE∥y轴,作点D关于BC的对称点D′,则BD=BD′,过点D′作D′F⊥x轴,垂足为F.
∵B(6,0),C(0,6),
∴OB=OC.
∴∠OBC=45°.
∴∠OBC=∠EBC.
又∵∠D′BC=∠DBC,
∴∠DBE=∠D′BF.
在△DEB和△D′FB中,,
∴△DEB≌△D′FB.
∴D′F=ED=2,BF=BE=6.
∴点D′的坐标为(0,2).
设BD′的解析式为y=kx+2,将点B的坐标代入得:6k+2=0,解得k=﹣,
∴BD′的解析式为y=﹣x+2.
将y=﹣x+2代入y=﹣x2+2x+6得:﹣x+2=﹣x2+2x+6,整理得:3x2﹣14x﹣24=0,解得:x=6(舍去)或x=﹣.
将x=﹣代入得:y=﹣×(﹣)+2=+2=
∴点P的坐标为(﹣,).
2.解:(1)把y=0代入y=x+1得:x+1=0,解得:x=﹣1,
∴点A(﹣1,0).
将点A和点B的坐标代入抛物线的解析式得:,解得:b=﹣2,c=﹣3.
∴抛物线的解析式为y=x2﹣2x﹣3.
(2)如图1所示:
设点E的坐标为(x,x+1),则点F的坐标为F(x,x2﹣2x﹣3).
设EF=(x+1)﹣(x2﹣2x﹣3)=﹣x2+3x+4=﹣(x﹣)2+.
∴当x=时,EF有最大值.
将x=代入y=x+1得:y=.
∴E(,).
(3)如图2所示:过点E作PE⊥EF,交抛物线与点P或点P′,则yp=.
将y=代入抛物线的解析式得:x2﹣2x﹣3=,解得:x=1+,x=1﹣.
∴点P的坐标为(1﹣,)或(1+,).
3.解:(1)对于抛物线y=a(x+1)(x﹣3),令y=0,得到a(x+1)(x﹣3)=0,解得x=﹣1或3,
∴A(﹣1,0),B(3,0),
∴OB=3,
∵∠ABC=45°,
∴OC=OB=3,
∴C(0,3),把(0,3)代入y=a(x+1)(x﹣3)得到a=﹣1,
∴抛物线的解析式为y=﹣x2+2x+3.
(2)如图2中,作PH⊥AB于H,交BC于T.,作CE⊥PH于E,设P(m,﹣m2+2m+3).
∵B(3,0),C(0,3),
∴直线BC的解析式为y=﹣x+3,
∴T(m,﹣m+3),
∵S△PBC=S△PTC+S△PTB= PT CE+ PT BH=PT (CE+BH)= PT OB=×(﹣m2+3m)×3=3,
整理得m2﹣3m+2=0,
∴m=1或2,
∵∠PCB>45°,
∴m=1,
∴P(1,4).
(3)如图3中,作RM⊥DQ于M,连接EM.DH交AB于N.设D(n,﹣n2+2n+3).
∵PQ∥DE,PQ⊥DQ,DH⊥AB,
∴Q(n,4),
∴DE=2(n﹣1),DQ=4﹣(﹣n2+2n+3)=(n﹣1)2,
∴==,==,
∴=,
∵∠EDQ=∠EDH=90°,
∴△EDQ∽△HDE,
∴∠DEQ=∠EHD,
∵∠DEQ+∠EQD=90°,
∴∠EHD+∠EQD=90°,
∴∠HEQ=90°,
∵∠REH+∠RMH=180°,
∴E、H、M、R四点共圆,
∴∠ERH=∠EMH,
∴tan∠ERH=tan∠EMD==,
∴DM=(n﹣1),
∴QM=(n﹣1)2﹣(n﹣1),
∵RM∥DE,
∴=,
∴RM=2n﹣,
∴R[﹣n+,4﹣(n﹣1)2+(n﹣1)],
把点R坐标代入y=﹣x2+2x+3得到,4﹣(n﹣1)2+(n﹣1)=﹣(﹣n+)2+2(﹣n+)+3,
解得n=,
∴D(,).
4.解:(1)由y=x2﹣x﹣3得到:y=(x﹣4)(x﹣2)或y=(x﹣1)2﹣,
所以 A(﹣2,0),B(4,0),
令x=0,则y=﹣3,
所以 C(0,﹣3);
综上所述,A(﹣2,0),B(4,0),C(0,﹣3);
故答案是:(﹣2,0),(4,0),(0,﹣3);
(2)①∵A(﹣2,0),B(4,0),
∴AB=6,
由BP=BQ得到:6﹣3t=t,
解得t=;
②∵B(4,0),C(0,﹣3),
∴OB=4,OC=3,
∴BC==5.
i)如图1,当∠BPQ=90°时,△BPQ∽△BOC,则=,即=,
解得t=;
ii)如图2,当∠BQP=90°时,△BPQ∽△BCO,则=,即=,
解得t=
综上所述,t的值是:或.
5.解:(1)∵一次函数y=x+m(m为常数)的图象与x轴交于点A(﹣3,0),
∴0=×(﹣3)+m,解得m=,
∴一次函数解析式为y=x+,
∴C点坐标为(0,).
∵以直线x=1为对称轴的抛物线y=ax2+bx+c(a、b、c为常数,且a≠0)经过A(﹣3,0)、C(0,),
∴,解得,
∴抛物线的函数表达式为y=﹣x2+x+;
(2)存在.设Q(x,﹣x2+x+).
①当点C为直角顶点时,如图,作CQ⊥AC交抛物线于点Q,QE⊥y轴于E.
在△ACO与△CQE中,
,
∴△ACO∽△CQE,
∴=,即=,
解得x1=5.2,x2=0(不合题意舍去);
②当点A为直角顶点时,如图,作AQ′⊥AC交抛物线于点Q′,Q′E′⊥x轴于E.
在△ACO与△Q′AE′中,
,
∴△ACO∽△Q′AE′,
∴=,即=,
解得x1=8.2,x2=﹣3(不合题意舍去).
综上所述:Q点的横坐标为5.2或8.2;
(3)∵y=﹣x2+x+与x轴交于A(﹣3,0)、B两点,对称轴为直线x=1,
∴B点坐标为(5,0),
∵C(0,),
∴直线BC的解析式为y=﹣x+,
当x=1时,y=﹣×1+=3,
∴P(1,3).
设过点P的直线为:y=kx+3﹣k,
把y=kx+3﹣k代入y=﹣x2+x+,
得kx+3﹣k=﹣x2+x+,
整理得,x2+(4k﹣2)x﹣4k﹣3=0,
∴x1+x2=2﹣4k,x1x2=﹣4k﹣3,y1﹣y2=k(x1﹣x2),
∴(x1﹣x2)2=(x1+x2)2﹣4x1x2=(2﹣4k)2﹣4(﹣4k﹣3)=16k2+16,
∴M1M2===4(1+k2),
同理:M1P==,
M2P=,
∴M1P M2P= =|(x1﹣1)(x2﹣1)| (1+k2)=4(1+k2),
∴=1为定值.
6.解:(1)∵直线y=kx﹣7与y轴的负半轴交于点C
∴C(0,﹣7),
∴OC=7,
∵抛物线y=ax2+bx+14a经过点C,
∴14a=﹣7,
∴a=﹣,
∴y=﹣x2+bx﹣7,
∵OA:OC=2:7.
∴OA=2,
∴A(2,0)
∵抛物线y=﹣x2+bx﹣7经过点A,
∴b=
∴抛物线的解析式为y=﹣x2+x﹣7,
(2)如图1,
∵抛物线y=﹣x2+x﹣7经过B点,
令y=0解得x=7或x=2(舍去),
∴B(7,0),
∴OB=7,
∴OC=OB,
∴∠OCB=∠OBC=45°
过点P作PF⊥x轴于点G,交CB延长线于点F,则PF∥y轴,
∴∠CFG=∠OCB=45°,
∴BF=GF,
过P作PE⊥BC于点E,
∵PD=PB,
∴∠PBD=∠PDB,
∴tan∠PBD=tan∠PDB=2,
∴PE=2BE,
∵EF=PE,
∴BF=BE,
∴PF=PE=2 BE=2 BF=4GF,
∴PG=3GF,
∵直线y=kx﹣7过B点,
∴k=1,
∴y=x﹣7,
设F(m,m﹣7),则P(m,﹣3(m﹣7)),
∵点P在抛物线y=﹣x2+x﹣7上,
∴﹣3(m﹣7)=﹣m2+m﹣7,
解得m=7(舍去)或m=8,
∴P(8,﹣3);
(3)如图2,当DP∥QR时,即四边形DQRP是平行四边形,
∵B(7,0),Q(7,m)
∴BQ∥y轴
过P作PN∥BQ,过D作DN⊥BQ交PN于点N,
过R作RM⊥BQ于点M.
设PD交BQ于点T,DN交BM于点I,
∴∠DTB=∠DPN,∠PTQ=∠RQM,
∵∠DTB=∠PTQ,
∴∠DPN=∠RQM,
∵四边形DPRQ是平行四边形,
∴DP=RQ,
在△RMQ和△DNP中,
,
∴△RMQ≌△DNP(AAS),
∴RM=DN,MQ=PN,
由(2)可求F(8,1),GF=1,BD=2BE=2BF=2 GF=2 ,
∵∠QBC=45°,∴BI=DI=2,
∴D(5,﹣2),
设R点的横坐标为t,
∵RM=DN,
∴t﹣7=8﹣5,
解得t=10,
∵点R在抛物线y=﹣x2+x﹣7 上,
∴当t=10时,﹣×102+×10﹣7=﹣12,
∴R(10,﹣12),
∵MQ=PN,
∴3﹣2=﹣12﹣n,
∴n=﹣11,
∴R(10,﹣12),Q(7,﹣11),
如图3,当DR∥QP时,即四边形DQPR是平行四边形
同理可求得R(6,2),Q(7,﹣7).
7.解:(1)因为抛物线y=ax2+bx+c经过A(﹣2,0)、B(4,0)两点,
所以可以假设y=a(x+2)(x﹣4),
∵OC=2OA,OA=2,
∴C(0,4),代入抛物线的解析式得到a=﹣,
∴y=﹣(x+2)(x﹣4)或y=﹣x2+x+4或y=﹣(x﹣1)2+.
(2)如图1中,由题意,点P在y轴的右侧,作PE⊥x轴于E,交BC于F.
∵CD∥PE,
∴△CMD∽△FMP,
∴m==,
∵直线y=kx+1(k>0)与y轴交于点D,则D(0,1),
∵BC的解析式为y=﹣x+4,
设P(n,﹣n2+n+4),则F(n,﹣n+4),
∴PF=﹣n2+n+4﹣(﹣n+4)=﹣(n﹣2)2+2,
∴m==﹣(n﹣2)2+,
∵﹣<0,
∴当n=2时,m有最大值,最大值为,此时P(2,4).
(3)存在这样的点Q、N,使得以P、D、Q、N四点组成的四边形是矩形.
①当DP是矩形的边时,有两种情形,
如图2﹣1中,四边形DQNP是矩形时,
有(2)可知P(2,4),代入y=kx+1中,得到k=,
∴直线DP的解析式为y=x+1,可得D(0,1),E(﹣,0),
由△DOE∽△QOD可得=,
∴OD2=OE OQ,
∴1= OQ,
∴OQ=,
∴Q(,0).
根据矩形的性质,将点P向右平移个单位,向下平移1个单位得到点N,
∴N(2+,4﹣1),即N(,3)
b、如图2﹣2中,四边形PDNQ是矩形时,
∵直线PD的解析式为y=x+1,PQ⊥PD,
∴直线PQ的解析式为y=﹣x+,
∴Q(8,0),
根据矩形的性质可知,将点D向右平移6个单位,向下平移4个单位得到点N,
∴N(0+6,1﹣4),即N(6,﹣3).
②当DP是对角线时,设Q(x,0),则QD2=x2+1,QP2=(x﹣2)2+42,PD2=13,
∵Q是直角顶点,
∴QD2+QP2=PD2,
∴x2+1+(x﹣2)2+16=13,
整理得x2﹣2x+4=0,方程无解,此种情形不存在,
综上所述,满足条件的点N坐标为(,3)或(6,﹣3).
8.解:(1)∵点A(﹣1,0),B(5,0)在抛物线y=ax2+bx﹣5上,
∴,
解得,
∴抛物线的表达式为y=x2﹣4x﹣5,
(2)设H(t,t2﹣4t﹣5),
∵CE∥x轴,
∴点E的纵坐标为﹣5,
∵E在抛物线上,
∴x2﹣4x﹣5=﹣5,
∴x=0(舍)或x=4,
∴E(4,﹣5),
∴CE=4,
∵B(5,0),C(0,﹣5),
∴直线BC的解析式为y=x﹣5,
∴F(t,t﹣5),
∴HF=t﹣5﹣(t2﹣4t﹣5)=﹣(t﹣)2+,
∵CE∥x轴,HF∥y轴,
∴CE⊥HF,
∴S四边形CHEF=CE HF=﹣2(t﹣)2+,
∴H(,﹣);
(3)如图2,∵K为抛物线的顶点,
∴K(2,﹣9),
∴K关于y轴的对称点K'(﹣2,﹣9),
∵M(4,m)在抛物线上,
∴M(4,﹣5),
∴点M关于x轴的对称点M'(4,5),
∴直线K'M'的解析式为y=x﹣,
∴P(,0),Q(0,﹣).
9.(1)解:y=x2+2x=(x+1)2﹣1,
∴顶点A(﹣1,﹣1);
由,解得:或
∴B(﹣2,0),C(1,3);
(2)证明:∵A(﹣1,﹣1),B(﹣2,0),C(1,3),
∴AB==,
BC==3,
AC==2,
∴AB2+BC2=AC2,==,
∴∠ABC=90°,
∵OD=1,CD=3,
∴=,
∴,∠ABC=∠ODC=90°,
∴△ODC∽△ABC;
(3)存在这样的P点,
设M(x,0),则P(x,x2+2x),
∴OM=|x|,PM=|x2+2x|,
当以O,P,M为顶点的三角形与△ABC相似时,
有=或=,
由(2)知:AB=,CB=3,
①当=时,则=,
当P在第二象限时,x<0,x2+2x>0,
∴,解得:x1=0(舍),x2=﹣,
当P在第三象限时,x<0,x2+2x<0,
∴=,解得:x1=0(舍),x2=﹣,
②当=时,则=3,
同理代入可得:x=﹣5或x=1(舍),
综上所述,存在这样的点P,坐标为(﹣,﹣)或(﹣,)或(﹣5,15).
10.解:(1)∵抛物线y=﹣x2+bx+c经过点A(5,)、点B(9,﹣10),
∴,
解得,
∴抛物线对应的函数表达式为y=﹣x2+2x﹣1;
(2)由抛物线可得,C(0,﹣1),B(9,﹣10),
∴直线BC为:y=﹣x﹣1,
设点P的坐标为(m,﹣m2+2m﹣1),则E(m,﹣m﹣1),
∴PE=﹣m2+2m﹣1﹣(﹣m﹣1)=﹣m2+3m,
∴四边形AECP的面积=△APE面积+△CPE面积
=×(﹣m2+3m)×m+×(﹣m2+3m)×(5﹣m)
=(﹣m2+3m)
=﹣m2+m,
=﹣(m﹣)2+,
∴当m=时,﹣m2+2m﹣1=,
∴点P坐标为( ,);
(3)①过点B作BH⊥y轴于H,
∵C(0,﹣1),B(9,﹣10),
∴CH=BH=9,
∴∠BCH=45°,
∵∠PCB=90°,CF平分∠PCB,
∴∠BCF=45°,
∴∠FCH=90°,即CF∥x轴,
当y=﹣1时,﹣1=﹣x2+2x﹣1,
解得x1=0,x2=6,
∴F(6,﹣1),
∵CP⊥CB,C(0,﹣1),
∴直线CP为:y=x﹣1,
当x﹣1=﹣x2+2x﹣1时,解得x1=0,x2=3,
当x=3时,y=2,
∴P(3,2);
②∵直线CB:y=﹣x﹣1,直线PF:y=﹣x+5,
∴CB∥PF,
∴∠BCF=∠PFC=45°,
∴在直线CF上存在满足条件的点Q,
设Q(t,﹣1),
由题可得CF=6,CB=9,PF=3,
(ⅰ)如图所示,当△PFQ1∽△BCF时,
=,即=,
解得t=4,
∴Q1(4,﹣1);
(ⅱ)如图所示,当△PFQ∽△FCB时,
=,即=,
解得t=﹣3,
∴Q2(﹣3,﹣1).
综上所述,点Q的坐标为(4,﹣1)或(﹣3,﹣1).
同课章节目录
