25.1.2概率的意义

课件24张PPT。25.1.2概率 什么是必然事件?知识回顾 在一定条件下重复进行试验时,在每次试验
中都必然发生的事件叫必然事件什么是不可能事件? 在一定条件下重复进行试验时,在每次试验
中都不会发生的事件叫不可能事件
什么是随机事件? 在一定条件下,可能发生也可能不发生的事件,
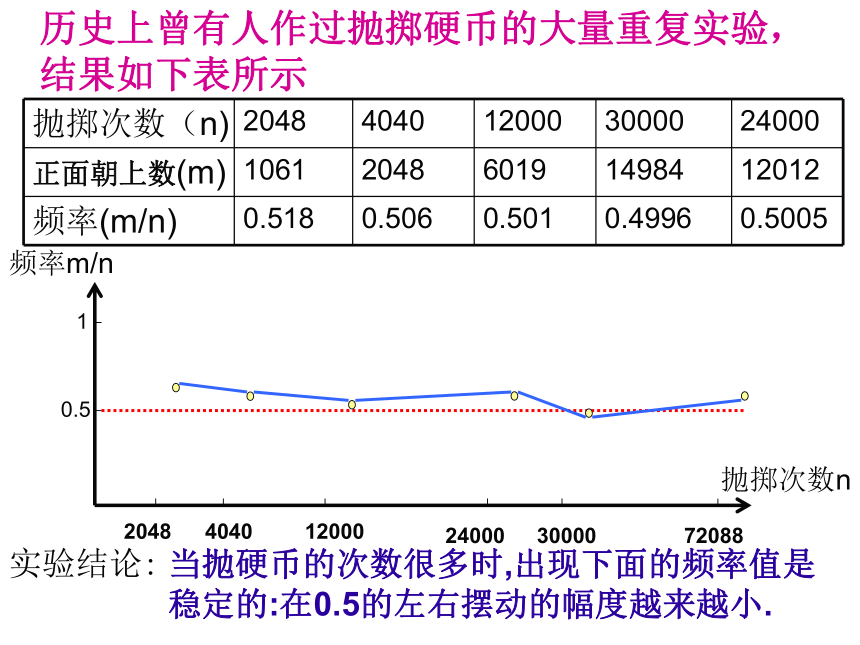
叫随机事件 下列事件中哪些事件是必然事件？哪些是不可能事件？哪些事件是随机事件？(1)抛出的铅球会下落（２）某运动员百米赛跑的成绩为２秒（３）买到的电影票，座位号为单号（４）ｘ２＋１是正数（５）投掷硬币时，国徽朝上必然事件不可能事件随机事件必然事件随机事件探究：投掷硬币时，国徽朝上的可能性有多大？ 在同样条件下，随机事件可能发生，也可能不发生，我们关心的是它发生的可能性到底有多大呢？这是我们下面要讨论的问题。历史上曾有人作过抛掷硬币的大量重复实验，
结果如下表所示实验结论:当抛硬币的次数很多时,出现下面的频率值是
稳定的:在0.5的左右摆动的幅度越来越小. 我们知道,当抛掷一枚硬币时,要么出现正面,要么出现反面,
它们是随机的.通过上面的试验,我们发现在大量试验中出现正
面的可能为0.5,那么出现反面的可能为多少呢? 这就是为什么我们在抛一次硬币时,说出现正面的
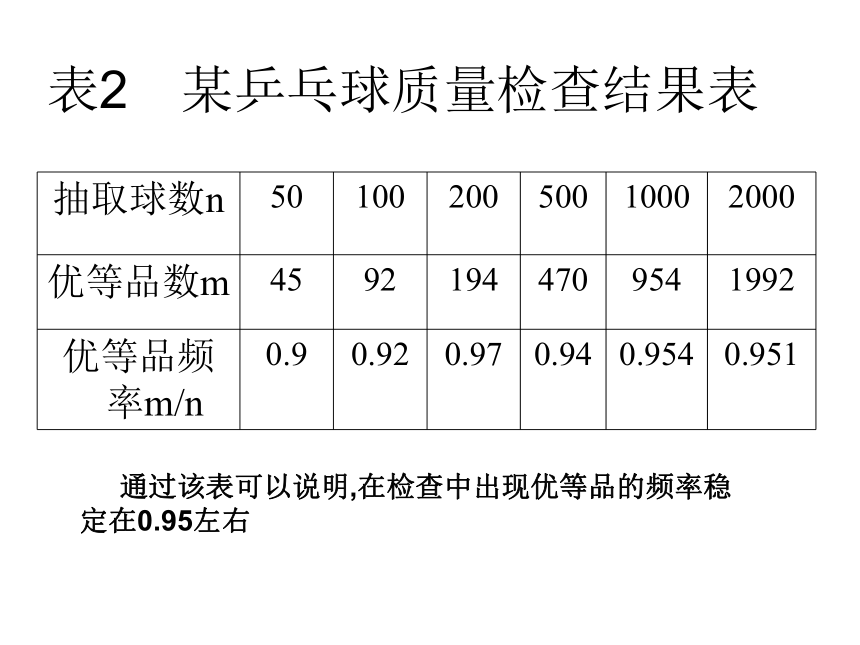
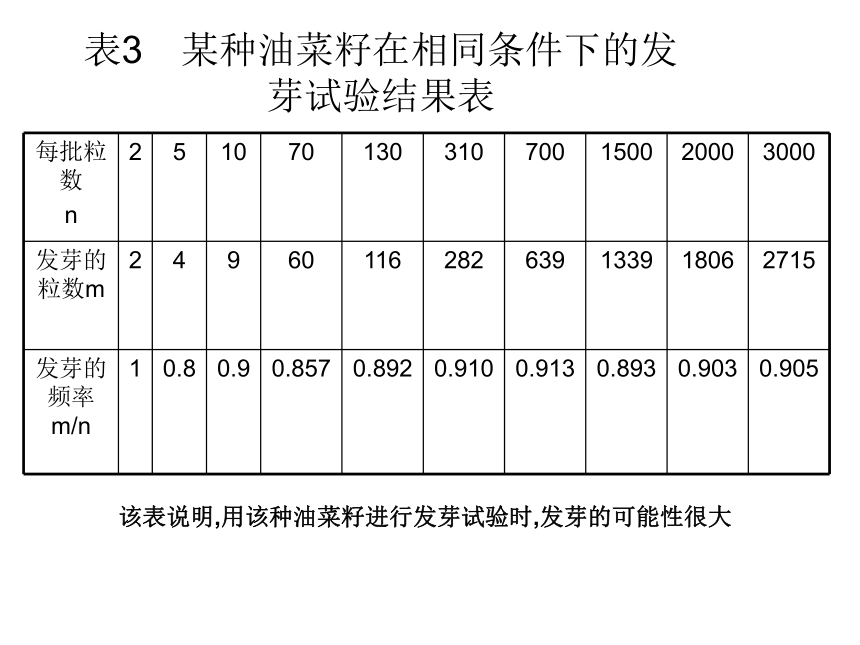
可能为0.5,出现反面的可能为0.5.出现反面的可能也为0.5表2　某乒乓球质量检查结果表 通过该表可以说明,在检查中出现优等品的频率稳定在0.95左右表3　某种油菜籽在相同条件下的发芽试验结果表该表说明,用该种油菜籽进行发芽试验时,发芽的可能性很大 一般地，在大量重复进行同一试验时，事件A发生的频率m/n稳定在某个常数p的附近，那么这个常数p就叫做事件A的概率，
记作P（A）=P.概率的定义 上面我们用随机事件发生的频率逐渐稳定到的常数来刻画随机事件发生的可能性的大小.思考？P(必然事件)＝1P(不可能事件)＝0 我们知道,必然事件在每次试验中都会发生,
不可能事件在每次试验中都不可能发生,那么
必然事件的概率和不可能事件的概率分别是
多少呢？.
记随机事件A在n次试验中发生了m次，那么有0≤m≤n,
0≤m/n≤1
于是可得　　0≤P(A) ≤1.
例１：对一批衬衫进行抽查，结果如下表：0.880.890.9010.905求抽取一件衬衫是优等品的概率约是多少？抽取衬衫2000件，约有优质品几件？解:由图可知,试验中优等品出现的概率约为0.9,即抽取
一件衬衫为优等品的概率为0.9,抽取2000件衬衫中
有优等品的件数可能为1800件.某射手进行射击，结果如下表所示：例２填表(2)这个射手射击一次，击中靶心的概率是多少？０.５(3)这射手射击1600次，击中靶心的次数可能是　　。8000.650.580.520.510.50例1：
问题（1）掷一枚一硬币,正面向上的概率是多少？
问题（2）抛掷一个骰子，它落地时向上的的数为
① 2的概率是多少？
②落地时向上的数是3的倍数的概率是多少？
③点数为奇数的概率是多少？
④点数大于2且小于5的数的概率是多少？ 做一做 例2.如图：是一个转盘，转盘分成7个相同的扇形，颜色分为红黄绿三种，指针固定，转动转盘后任其自由停止，某个扇形会停在指针所指的位置，（指针指向交线时当作指向右边的扇形）求下列事件的概率:（1）指向红色；（2） 指向红色或黄色；（3） 不指向红色。解：一共有7中等可能的结果。
（1）指向红色有3种结果，
P(红色)=_____
（2）指向红色或黄色一共有5种
等可能的结果，P( 红或黄）=_______
（3）不指向红色有4种等可能的结果
P( 不指红）= ________3/75/74/7练一练 例3：如图：计算机扫雷游戏，在9×9个小方格中，随机埋藏着10个地雷，每个小方格只有1个地雷，，小王开始随机踩一个小方格，标号为3，在3的周围的正方形中有3个地雷，我们把他的区域记为A区，A区外记为B区，，下一步小王应该踩在A区还是B区？ 由于3/8大于7/72，
所以第二步应踩B区解：A区有8格3个雷，
遇雷的概率为3/8， B区有9×9-9=72个小方格，
还有10-3=7个地雷， 遇到地雷的概率为7/72， 练习１．抛掷一只纸杯的重复试验的结果如下表：(1) 在表内的空格处填上适当的数（２）任意抛掷一只纸杯，杯口朝上的概率为　　　．0.24750.252.明天下雨的概率为95％，那么下列说法错误的是（ ）(A) 明天下雨的可能性较大(B) 明天不下雨的可能性较小(C) 明天有可能是晴天(D) 明天不可能是晴天3.有一种麦种，播种一粒种子，发芽的概率是98％，成苗的概率为85％.若要得到10 000株麦苗,则大约需要 ________ 粒麦种.(精确到1粒)D120054.对某服装厂的成品西装进行抽查,结果如下表:(1)请完成上表(2)任抽一件是次品的概率是多少?(3)如果销售1 500件西服,那么需要准备多少件正品西装供买到次品西装的顾客调换?0.970.990.980.980.021．随机掷一枚均匀的硬币两次，两次正面都朝上的概率是（ ）．
A． B． C． D．1．
2．从甲地到乙地可坐飞机、火车、汽车，从乙地到丙地可坐飞机、火车、汽车、轮船，某人乘坐以上交通工具，从甲地经乙地到丙地的方法有（ ）种．
A．4 B．64 C．12 D．81．比一比 3.中央电视台“幸运52”栏目中的“百宝箱”互动环节，是一种竞猜游戏，游戏规则如下：在20个商标中，有5个商标牌的背面注明了一定的奖金额，其余商标的背面是一张苦脸，若翻到它就不得奖。参加这个游戏的观众有三次翻牌的机会。某观众前两次翻牌均得若干奖金，如果翻过的牌不能再翻，那么这位观众第三次翻牌获奖的概率是（ ）．
A. B. C. D. 4、有100张卡片（从1号到100号），从中任取1张，取到的卡号是7的倍数的概率为（　）。5、某组16名学生，其中男女生各一半，把全组学生分成人数相等的两个小组，则分得每小组里男、女人数相同的概率是（　）6一个口袋内装有大小相同的1个白球和已编有不同号码的3个黑球，从中摸出2个球.
　（1）共有多少种不同的结果？
　（2）摸出2个黑球有多种不同的结果？
　（3）摸出两个黑球的概率是多少？课堂小结：１、必然事件、不可能事件、随机事件的定义。２、必然事件Ａ，则Ｐ（Ａ）＝１；
　　不可能事件Ｂ，则Ｐ（Ｂ）＝０；
　　随机事件Ｃ，则０＜Ｐ（Ｃ）＜１。３、求概率的方法：通过大量反复试验，统计出这件事发生的频率近似地做为它的概率。４、概率的定义及基本性质。