北京市朝阳区2024-2025学年八年级上学期期末考试数学试卷(含答案)
文档属性
| 名称 | 北京市朝阳区2024-2025学年八年级上学期期末考试数学试卷(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 769.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-08 00:00:00 | ||
图片预览



文档简介
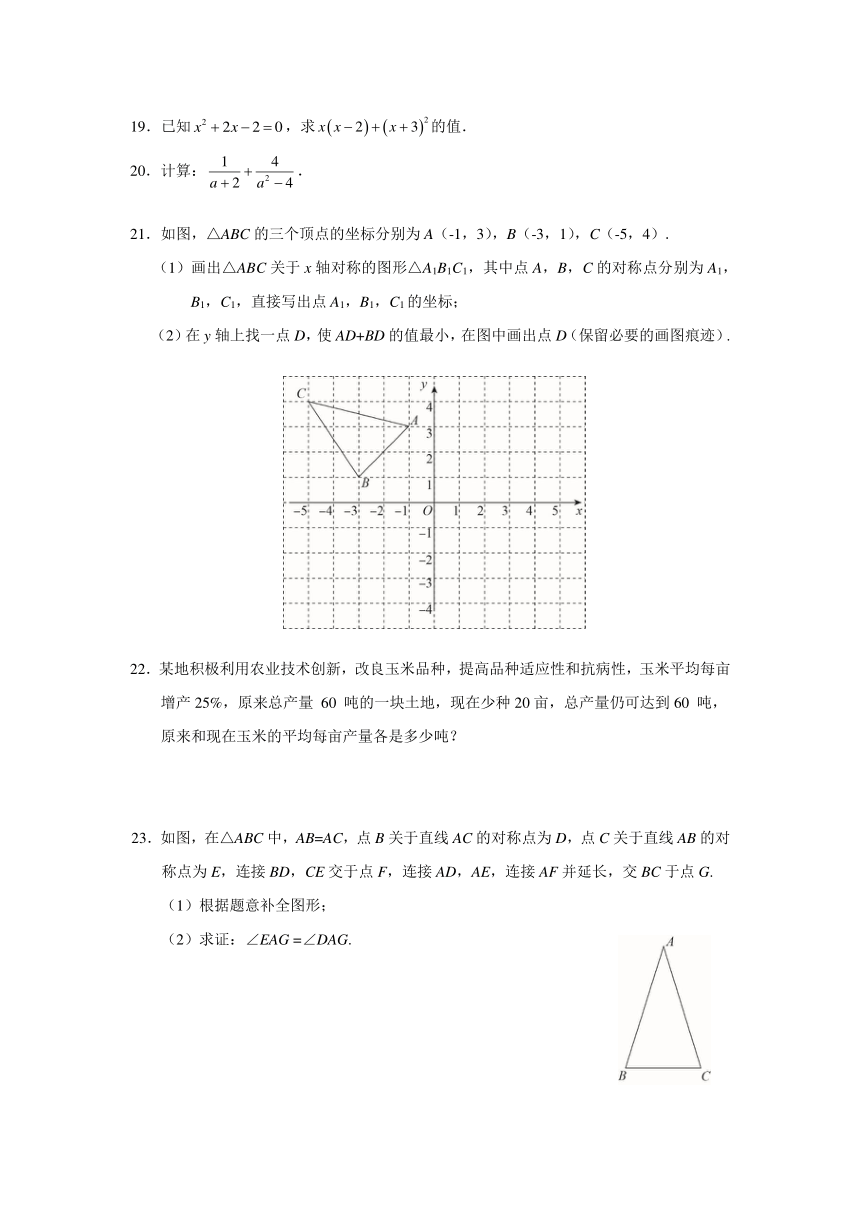
北京市朝阳区2024~2025学年度第一学期期末检测
八年级数学试卷 (选用) 2025.1
(考试时间90分钟 满分100分)
学校 班级 姓名 考号_______________
考 生 须 知 1.本试卷共6页,共三道大题,26道小题. 2.在试卷和答题卡上认真填写学校、班级、姓名、考号. 3.试题答案一律填涂或书写在答题卡上,在试卷上作答无效. 4.在答题卡上,选择题、作图题用2B铅笔作答,其他试题用黑色字迹签字笔作答. 5.考试结束,请将本试卷、答题卡和草稿纸一并交回.
一、选择题(共24分,每题3分)
下面1-8题均有四个选项,符合题意的选项只有一个.
1.下列图形中,为轴对称图形的是
(A) (B) (C) (D)
2.下列长度的三条线段,能组成三角形的是
(A)2 3 5 (B)3 5 9 (C)2 5 5 (D)5 12 7
3.下列图形中,具有稳定性的是
(A) (B) (C) (D)
4.如果把分式中的x,y都扩大3倍,那么分式的值
(A)扩大9倍 (B)扩大3倍 (C)缩小3倍 (D)不变
5.将一副三角尺按如图方式放置,则图中∠ABC的度数为
(A)75°
(B)105°
(C)120°
(D)135°
6.根据工信部《首台(套)重大技术装备推广应用指导目录(2024版)》信息,氟化氩光刻机的分辨率不超过65 nm,已知1 nm=10-9 m,65 nm=x m,则x的值为
(A)6.5×10-8 (B)6.5×10-9 (C)6.5×10-10 (D)6.5×10-11
7.下面是“作∠AOB 的角的平分线”的尺规作图方法:
上述方法通过判定△POC≌△POD得到∠POC=∠POD,其中判定△POC≌△POD的依据是
(A)两角分别相等且其中一组等角的对边相等的两个三角形全等
(B)两边和它们的夹角分别相等的两个三角形全等
(C)两角和它们的夹边分别相等的两个三角形全等
(D)三边分别相等的两个三角形全等
8.在△ABC中,∠A=90°,AB=AC,将△ABC按如图所示的方式依次折叠:
有下面四个结论:
①DE平分∠FDC;②BF=AD;③∠ADB=3∠BDF;④△FED的周长等于BC的长.
所有正确结论的序号为
(A)①③ (B)①③④ (C)②③④ (D)①②③④
二、填空题(共24分,每题3分)
9. 计算:=_____.
10. 若分式有意义,则实数x的取值范围是_____.
11.正六边形的外角和为_____°.
12.方程的解为 .
13.如图所示的网格为正方形网格,则∠2-∠1= °.
14.如图,OA平分∠MON,点P在OA上,点B,C分别在OM,ON边上,有如下条件:①PB⊥OM,PC⊥ON;②OB=OC;③∠OPB=∠OPC.选取其中一个可以得到PB=PC的条件,序号是 .(写出所有可能的情况.)
15.如图,在3×3的正方形网格中,△ABC的3个顶点均在正方形的顶点(格点)上,这样的三角形叫做格点三角形. E为网格图中与△ABC全等的格点三角形(△ABC除外)的一个顶点,其对应点为C.若在平面直角坐标系中,点A的坐标为(0,3),点C的坐标为(2,0),点E在坐标轴上,则点E的坐标为 .
16.由于科技创新与产业结构的优化,某种产品的原材料实现了一定幅度的降价,因而厂家决定对产品进行降价,现有三种方案:①第一次降价a%,第二次降价b%;②第一次降价b%,第二次降价a%;③第一、二次降价均为%.
记降价后方案①的产品价格为A,方案②的产品价格为B,方案③的产品价格为C.
若a=10,b=15,则A B(填“>”“<”或“=”);若a,b均为正数,则A,B,C的大小关系是 .
三、解答题(共52分,第17-24题,每题5分,第25-26题,每题6分)
17.计算:.
18.如图,点A,B,C,D在一条直线上,∠A=∠FBD,AC=BD, EC∥FD.
求证:AE=BF.
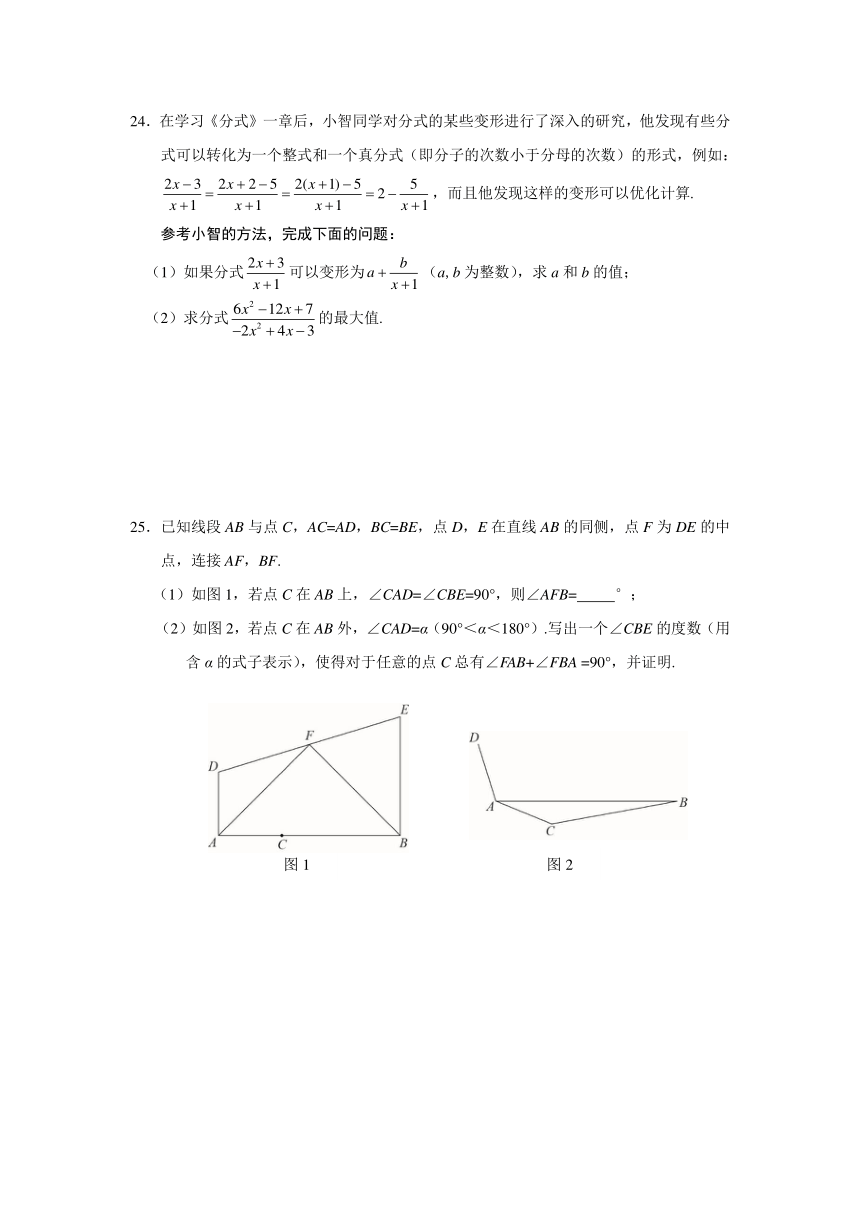
19.已知,求的值.
20.计算:.
21.如图,△ABC的三个顶点的坐标分别为A(-1,3),B(-3,1),C(-5,4).
(1)画出△ABC关于x轴对称的图形△A1B1C1,其中点A,B,C的对称点分别为A1,B1,C1,直接写出点A1,B1,C1的坐标;
(2)在y轴上找一点D,使AD+BD的值最小,在图中画出点D(保留必要的画图痕迹).
22.某地积极利用农业技术创新,改良玉米品种,提高品种适应性和抗病性,玉米平均每亩增产25%,原来总产量 60 吨的一块土地,现在少种20亩,总产量仍可达到60 吨,原来和现在玉米的平均每亩产量各是多少吨?
23.如图,在△ABC中,AB=AC,点B关于直线AC的对称点为D,点C关于直线AB的对称点为E,连接BD,CE交于点F,连接AD,AE,连接AF并延长,交BC于点G.
(1)根据题意补全图形;
(2)求证:∠EAG =∠DAG.
24.在学习《分式》一章后,小智同学对分式的某些变形进行了深入的研究,他发现有些分式可以转化为一个整式和一个真分式(即分子的次数小于分母的次数)的形式,例如:,而且他发现这样的变形可以优化计算.
参考小智的方法,完成下面的问题:
(1)如果分式可以变形为(a,b为整数),求a和b的值;
(2)求分式的最大值.
25.已知线段AB与点C,AC=AD,BC=BE,点D,E在直线AB的同侧,点F为DE的中点,连接AF,BF.
(1)如图1,若点C在AB上,∠CAD=∠CBE=90°,则∠AFB= °;
(2)如图2,若点C在AB外,∠CAD=α(90°<α<180°).写出一个∠CBE的度数(用含α的式子表示),使得对于任意的点C总有∠FAB+∠FBA =90°,并证明.
26.在平面直角坐标系xOy中,对于点P与直线l给出如下定义:若点P关于直线l的对称点到y轴的距离不超过1,则称点P存在关于直线l的近距对称点.
(1)在点(,0),(-1,3),(2,2)中,存在关于y轴的近距对称点的是 ;
(2)如图,点A在x轴正半轴上,点B在第一象限,∠AOB=60°,若点P(t,0)存在关于直线OB的近距对称点,直接写出t的取值范围;
(3)已知直线l与x轴交于点A,与y轴正半轴交于点B,若经过点C(-1,1)与点O的直线上任意一点,都存在关于直线l的近距对称点,直接写出∠OAB的度数及点B到直线OC距离d的取值范围.
北京市朝阳区2024~2025学年度第一学期期末检测
八年级数学试卷参考答案及评分标准 2025.1
一、选择题(共24分,每题3分)
题号 1 2 3 4 5 6 7 8
答案 A C A D B A D B
题号 9 10 11 12
答案 360
题号 13 14 15 16
答案 90 ①②③ (1,0),(0,1),(0,2) =; A=B≤C
二、填空题(共24分,每题3分)
三、解答题(共52分,第17-24题,每题5分,第25-26题,每题6分)
17.解:
.
18.证明:∵EC∥FD,
∴∠ACE=∠D.
在△ACE和△BDF中,
∴△ACE≌△BDF.
∴AE=BF.
19.解:
.
∵,
∴.
∴原式=.
20.解:
.
21.解:(1)△A1B1C1如图所示:
点A1,B1,C1的坐标分别为(-1,-3),(-3,-1),(-5,-4);
(2)点D如图所示.
22.解:设原来玉米的平均每亩产量是x吨.
根据题意,得
.
解得.
经检验,是原分式方程的解,且符合题意.
.
答:原来玉米的平均每亩产量是0.6吨,现在玉米的平均每亩产量是0.75吨.
23.(1)补全的图形如图所示:
(2)证明:如图,设AC,BD交于点M, CE,AB交于点N.
∵AC=BC,
∴∠ABC=∠ACB.
∵点B与点D关于直线AC对称,
∴AC⊥BD,BM=DM.
∴∠BMC=90°,AB=AD.
∴∠BCM+∠CBM =90°,∠BAM=∠DAM.
同理,∠BCN+∠CBN =90°,∠CAN=∠EAN.
∴∠CBM =∠BCN,∠DAM =∠EAN.
∴FB =FC.
∴AG垂直平分BC.
∴∠BAG =∠CAG.
∴∠EAG =∠DAG.
24.解:(1)
.
∴.
(2)
.
∵,
∴.
∴.
∴.
∴原分式的最大值为.
25.(1)90;
(2)180°-α.
证明:如图,延长AF至G,使FG=AF,连接BG,EG.
∵F为DE的中点,
∴DF=EF.
∵∠AFD=∠GFE,
∴△ADF≌△GEF.
∴∠D=∠GEF,AD=GE.
∵AD=AC,
∴GE = AC.
在五边形ACBED中,
∠D+∠DAC+∠C +∠CBE +∠BED =540°.
∵∠CAD =α,∠CBE =180°-α,
∴∠D+∠C +∠BED =360°.
∴∠GEF+∠C +∠BED =360°.
∵∠GEF+∠GEB+∠BED =360°,
∴∠GEB=∠C .
∵BE=BC,
∴△GEB≌△ACB.
∴BG=BA.
∴BF⊥AG.
∴∠AFB=90°.
∴∠FAB+∠FBA =90°.
26.解:(1),.
(2).
(3)22.5°或67.5°;.
八年级数学试卷 (选用) 2025.1
(考试时间90分钟 满分100分)
学校 班级 姓名 考号_______________
考 生 须 知 1.本试卷共6页,共三道大题,26道小题. 2.在试卷和答题卡上认真填写学校、班级、姓名、考号. 3.试题答案一律填涂或书写在答题卡上,在试卷上作答无效. 4.在答题卡上,选择题、作图题用2B铅笔作答,其他试题用黑色字迹签字笔作答. 5.考试结束,请将本试卷、答题卡和草稿纸一并交回.
一、选择题(共24分,每题3分)
下面1-8题均有四个选项,符合题意的选项只有一个.
1.下列图形中,为轴对称图形的是
(A) (B) (C) (D)
2.下列长度的三条线段,能组成三角形的是
(A)2 3 5 (B)3 5 9 (C)2 5 5 (D)5 12 7
3.下列图形中,具有稳定性的是
(A) (B) (C) (D)
4.如果把分式中的x,y都扩大3倍,那么分式的值
(A)扩大9倍 (B)扩大3倍 (C)缩小3倍 (D)不变
5.将一副三角尺按如图方式放置,则图中∠ABC的度数为
(A)75°
(B)105°
(C)120°
(D)135°
6.根据工信部《首台(套)重大技术装备推广应用指导目录(2024版)》信息,氟化氩光刻机的分辨率不超过65 nm,已知1 nm=10-9 m,65 nm=x m,则x的值为
(A)6.5×10-8 (B)6.5×10-9 (C)6.5×10-10 (D)6.5×10-11
7.下面是“作∠AOB 的角的平分线”的尺规作图方法:
上述方法通过判定△POC≌△POD得到∠POC=∠POD,其中判定△POC≌△POD的依据是
(A)两角分别相等且其中一组等角的对边相等的两个三角形全等
(B)两边和它们的夹角分别相等的两个三角形全等
(C)两角和它们的夹边分别相等的两个三角形全等
(D)三边分别相等的两个三角形全等
8.在△ABC中,∠A=90°,AB=AC,将△ABC按如图所示的方式依次折叠:
有下面四个结论:
①DE平分∠FDC;②BF=AD;③∠ADB=3∠BDF;④△FED的周长等于BC的长.
所有正确结论的序号为
(A)①③ (B)①③④ (C)②③④ (D)①②③④
二、填空题(共24分,每题3分)
9. 计算:=_____.
10. 若分式有意义,则实数x的取值范围是_____.
11.正六边形的外角和为_____°.
12.方程的解为 .
13.如图所示的网格为正方形网格,则∠2-∠1= °.
14.如图,OA平分∠MON,点P在OA上,点B,C分别在OM,ON边上,有如下条件:①PB⊥OM,PC⊥ON;②OB=OC;③∠OPB=∠OPC.选取其中一个可以得到PB=PC的条件,序号是 .(写出所有可能的情况.)
15.如图,在3×3的正方形网格中,△ABC的3个顶点均在正方形的顶点(格点)上,这样的三角形叫做格点三角形. E为网格图中与△ABC全等的格点三角形(△ABC除外)的一个顶点,其对应点为C.若在平面直角坐标系中,点A的坐标为(0,3),点C的坐标为(2,0),点E在坐标轴上,则点E的坐标为 .
16.由于科技创新与产业结构的优化,某种产品的原材料实现了一定幅度的降价,因而厂家决定对产品进行降价,现有三种方案:①第一次降价a%,第二次降价b%;②第一次降价b%,第二次降价a%;③第一、二次降价均为%.
记降价后方案①的产品价格为A,方案②的产品价格为B,方案③的产品价格为C.
若a=10,b=15,则A B(填“>”“<”或“=”);若a,b均为正数,则A,B,C的大小关系是 .
三、解答题(共52分,第17-24题,每题5分,第25-26题,每题6分)
17.计算:.
18.如图,点A,B,C,D在一条直线上,∠A=∠FBD,AC=BD, EC∥FD.
求证:AE=BF.
19.已知,求的值.
20.计算:.
21.如图,△ABC的三个顶点的坐标分别为A(-1,3),B(-3,1),C(-5,4).
(1)画出△ABC关于x轴对称的图形△A1B1C1,其中点A,B,C的对称点分别为A1,B1,C1,直接写出点A1,B1,C1的坐标;
(2)在y轴上找一点D,使AD+BD的值最小,在图中画出点D(保留必要的画图痕迹).
22.某地积极利用农业技术创新,改良玉米品种,提高品种适应性和抗病性,玉米平均每亩增产25%,原来总产量 60 吨的一块土地,现在少种20亩,总产量仍可达到60 吨,原来和现在玉米的平均每亩产量各是多少吨?
23.如图,在△ABC中,AB=AC,点B关于直线AC的对称点为D,点C关于直线AB的对称点为E,连接BD,CE交于点F,连接AD,AE,连接AF并延长,交BC于点G.
(1)根据题意补全图形;
(2)求证:∠EAG =∠DAG.
24.在学习《分式》一章后,小智同学对分式的某些变形进行了深入的研究,他发现有些分式可以转化为一个整式和一个真分式(即分子的次数小于分母的次数)的形式,例如:,而且他发现这样的变形可以优化计算.
参考小智的方法,完成下面的问题:
(1)如果分式可以变形为(a,b为整数),求a和b的值;
(2)求分式的最大值.
25.已知线段AB与点C,AC=AD,BC=BE,点D,E在直线AB的同侧,点F为DE的中点,连接AF,BF.
(1)如图1,若点C在AB上,∠CAD=∠CBE=90°,则∠AFB= °;
(2)如图2,若点C在AB外,∠CAD=α(90°<α<180°).写出一个∠CBE的度数(用含α的式子表示),使得对于任意的点C总有∠FAB+∠FBA =90°,并证明.
26.在平面直角坐标系xOy中,对于点P与直线l给出如下定义:若点P关于直线l的对称点到y轴的距离不超过1,则称点P存在关于直线l的近距对称点.
(1)在点(,0),(-1,3),(2,2)中,存在关于y轴的近距对称点的是 ;
(2)如图,点A在x轴正半轴上,点B在第一象限,∠AOB=60°,若点P(t,0)存在关于直线OB的近距对称点,直接写出t的取值范围;
(3)已知直线l与x轴交于点A,与y轴正半轴交于点B,若经过点C(-1,1)与点O的直线上任意一点,都存在关于直线l的近距对称点,直接写出∠OAB的度数及点B到直线OC距离d的取值范围.
北京市朝阳区2024~2025学年度第一学期期末检测
八年级数学试卷参考答案及评分标准 2025.1
一、选择题(共24分,每题3分)
题号 1 2 3 4 5 6 7 8
答案 A C A D B A D B
题号 9 10 11 12
答案 360
题号 13 14 15 16
答案 90 ①②③ (1,0),(0,1),(0,2) =; A=B≤C
二、填空题(共24分,每题3分)
三、解答题(共52分,第17-24题,每题5分,第25-26题,每题6分)
17.解:
.
18.证明:∵EC∥FD,
∴∠ACE=∠D.
在△ACE和△BDF中,
∴△ACE≌△BDF.
∴AE=BF.
19.解:
.
∵,
∴.
∴原式=.
20.解:
.
21.解:(1)△A1B1C1如图所示:
点A1,B1,C1的坐标分别为(-1,-3),(-3,-1),(-5,-4);
(2)点D如图所示.
22.解:设原来玉米的平均每亩产量是x吨.
根据题意,得
.
解得.
经检验,是原分式方程的解,且符合题意.
.
答:原来玉米的平均每亩产量是0.6吨,现在玉米的平均每亩产量是0.75吨.
23.(1)补全的图形如图所示:
(2)证明:如图,设AC,BD交于点M, CE,AB交于点N.
∵AC=BC,
∴∠ABC=∠ACB.
∵点B与点D关于直线AC对称,
∴AC⊥BD,BM=DM.
∴∠BMC=90°,AB=AD.
∴∠BCM+∠CBM =90°,∠BAM=∠DAM.
同理,∠BCN+∠CBN =90°,∠CAN=∠EAN.
∴∠CBM =∠BCN,∠DAM =∠EAN.
∴FB =FC.
∴AG垂直平分BC.
∴∠BAG =∠CAG.
∴∠EAG =∠DAG.
24.解:(1)
.
∴.
(2)
.
∵,
∴.
∴.
∴.
∴原分式的最大值为.
25.(1)90;
(2)180°-α.
证明:如图,延长AF至G,使FG=AF,连接BG,EG.
∵F为DE的中点,
∴DF=EF.
∵∠AFD=∠GFE,
∴△ADF≌△GEF.
∴∠D=∠GEF,AD=GE.
∵AD=AC,
∴GE = AC.
在五边形ACBED中,
∠D+∠DAC+∠C +∠CBE +∠BED =540°.
∵∠CAD =α,∠CBE =180°-α,
∴∠D+∠C +∠BED =360°.
∴∠GEF+∠C +∠BED =360°.
∵∠GEF+∠GEB+∠BED =360°,
∴∠GEB=∠C .
∵BE=BC,
∴△GEB≌△ACB.
∴BG=BA.
∴BF⊥AG.
∴∠AFB=90°.
∴∠FAB+∠FBA =90°.
26.解:(1),.
(2).
(3)22.5°或67.5°;.
同课章节目录
