专题01 单选题(含解析)-2024-2025学年浙江地区八年级数学上学期期末备考真题分类汇编
文档属性
| 名称 | 专题01 单选题(含解析)-2024-2025学年浙江地区八年级数学上学期期末备考真题分类汇编 |  | |
| 格式 | doc | ||
| 文件大小 | 3.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-08 07:59:46 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
专题01 单选题
一.选择题(共60小题)
1.(2023秋 衢州期末)要说明命题“若|a|>|b|,则a>b”是假命题,能举的一个反例是( )
A.a=1,b=﹣2 B.a=2,b=1 C.a=4,b=﹣1 D.a=﹣3,b=﹣2
2.(2023秋 义乌市期末)人字梯中间一般会设计一“拉杆”,这样做的道理是( )
A.两点之间,线段最短
B.垂线段最短
C.两直线平行,内错角相等
D.三角形具有稳定性
3.(2023秋 金东区期末)如图,在直角坐标系中,正△OAB的边OB在x轴的正半轴上,若OA=2,则正△OAB绕着点B顺时针旋转120°后,点O的对应点坐标是( )
A.(2,0) B.(4,0) C. D.
4.(2024秋 江岸区校级期末)如图,△ABC≌△DEF,边BC和EF在同一条直线上.若BC=4cm,BF=6cm,则BE长为( )
A.1cm B.2cm C.3cm D.4cm
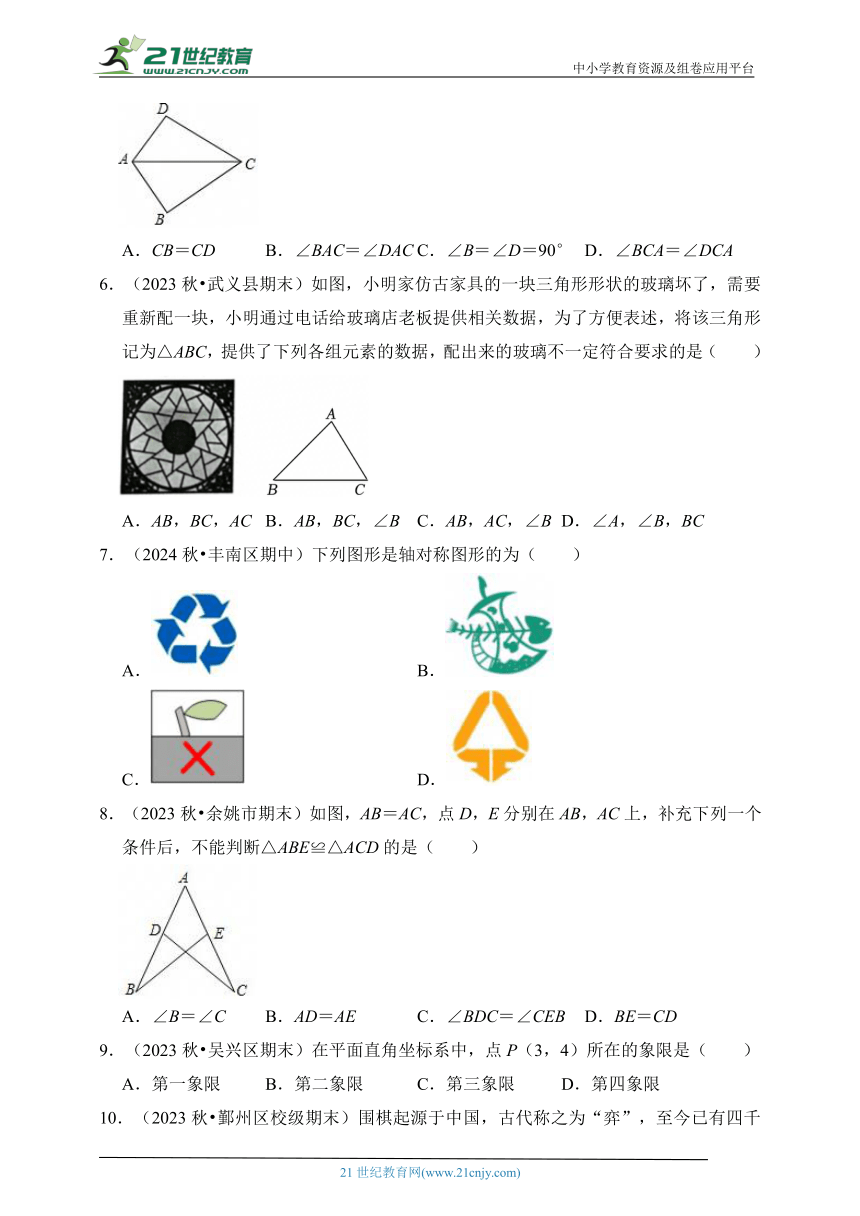
5.(2023秋 鄞州区期末)如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )
A.CB=CD B.∠BAC=∠DAC C.∠B=∠D=90° D.∠BCA=∠DCA
6.(2023秋 武义县期末)如图,小明家仿古家具的一块三角形形状的玻璃坏了,需要重新配一块,小明通过电话给玻璃店老板提供相关数据,为了方便表述,将该三角形记为△ABC,提供了下列各组元素的数据,配出来的玻璃不一定符合要求的是( )
A.AB,BC,AC B.AB,BC,∠B C.AB,AC,∠B D.∠A,∠B,BC
7.(2024秋 丰南区期中)下列图形是轴对称图形的为( )
A. B.
C. D.
8.(2023秋 余姚市期末)如图,AB=AC,点D,E分别在AB,AC上,补充下列一个条件后,不能判断△ABE≌△ACD的是( )
A.∠B=∠C B.AD=AE C.∠BDC=∠CEB D.BE=CD
9.(2023秋 吴兴区期末)在平面直角坐标系中,点P(3,4)所在的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
10.(2023秋 鄞州区校级期末)围棋起源于中国,古代称之为“弈”,至今已有四千多年的历史,下列由黑白棋子摆成的图案是轴对称图形的是( )
A. B.
C. D.
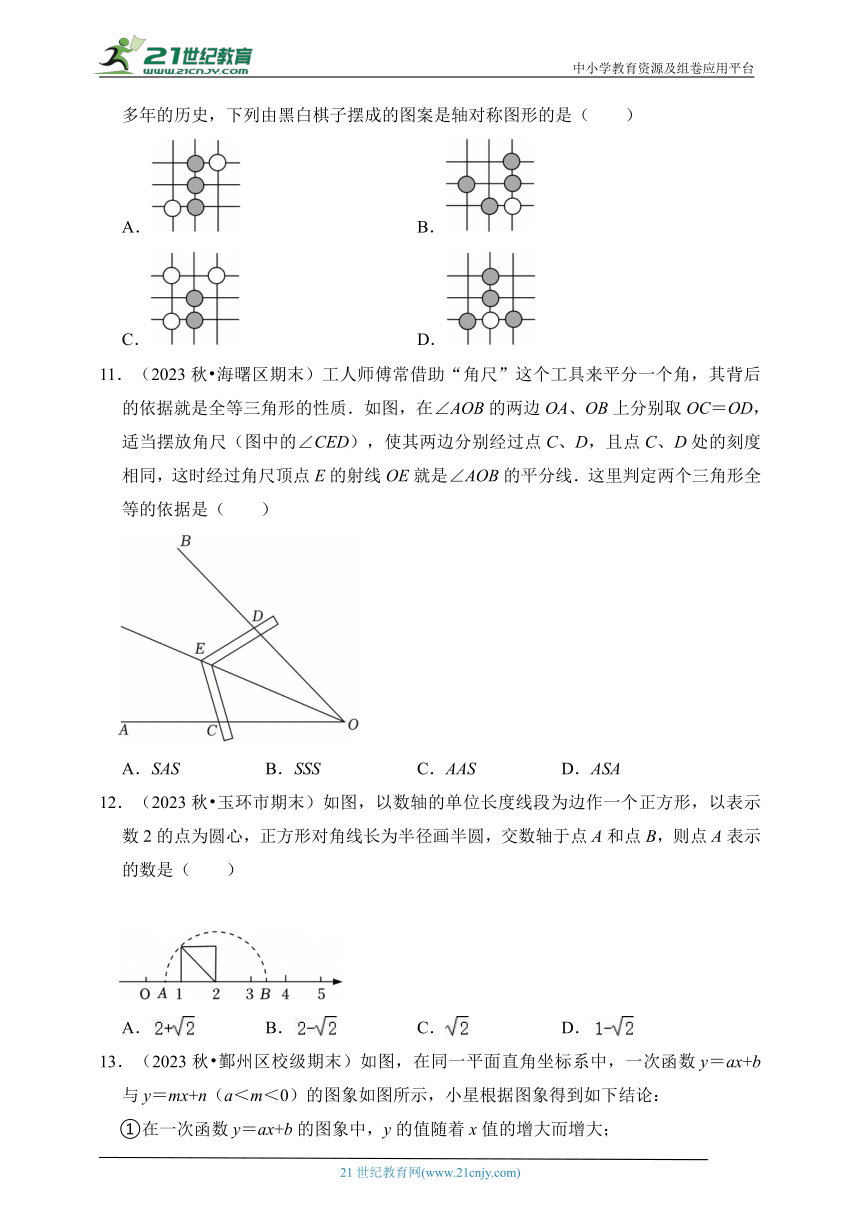
11.(2023秋 海曙区期末)工人师傅常借助“角尺”这个工具来平分一个角,其背后的依据就是全等三角形的性质.如图,在∠AOB的两边OA、OB上分别取OC=OD,适当摆放角尺(图中的∠CED),使其两边分别经过点C、D,且点C、D处的刻度相同,这时经过角尺顶点E的射线OE就是∠AOB的平分线.这里判定两个三角形全等的依据是( )
A.SAS B.SSS C.AAS D.ASA
12.(2023秋 玉环市期末)如图,以数轴的单位长度线段为边作一个正方形,以表示数2的点为圆心,正方形对角线长为半径画半圆,交数轴于点A和点B,则点A表示的数是( )
A. B. C. D.
13.(2023秋 鄞州区校级期末)如图,在同一平面直角坐标系中,一次函数y=ax+b与y=mx+n(a<m<0)的图象如图所示,小星根据图象得到如下结论:
①在一次函数y=ax+b的图象中,y的值随着x值的增大而增大;
②方程组的解为,
③当x=0时,ax+b=﹣1;
④方程mx+n=0的解为x=2;
⑤不等式mx+n≥ax+b的解集是x≥﹣3.
其中结论正确的个数是( )
A.1 B.2 C.3 D.4
14.(2023秋 鄞州区期末)若点A(﹣3,y1),B(2,y2),C(3,y3)是函数y=﹣x+2图象上的点,则( )
A.y1<y2<y3 B.y1>y2>y3 C.y1<y3<y2 D.y2>y3>y1
15.(2023秋 滨江区校级期末)不等式组有3个整数解,则a的取值范围是( )
A.5<a≤6 B.4<a≤5 C.4≤a<5 D.5≤a<6
16.(2023秋 台州期末)P是△ABC内一点,PD⊥BC,PE⊥AB,PF⊥AC,垂足分别为D,E,F,且PD=PE=PF,则点P是△ABC( )
A.三边垂直平分线的交点
B.三条角平分线的交点
C.三条高所在直线的交点
D.三条中线的交点
17.(2023秋 宁波期末)在平面直角坐标系中,直线y=2x﹣3与y轴的交点坐标是( )
A.(0,﹣3) B.(﹣3,0) C.(2,﹣3) D.(,0)
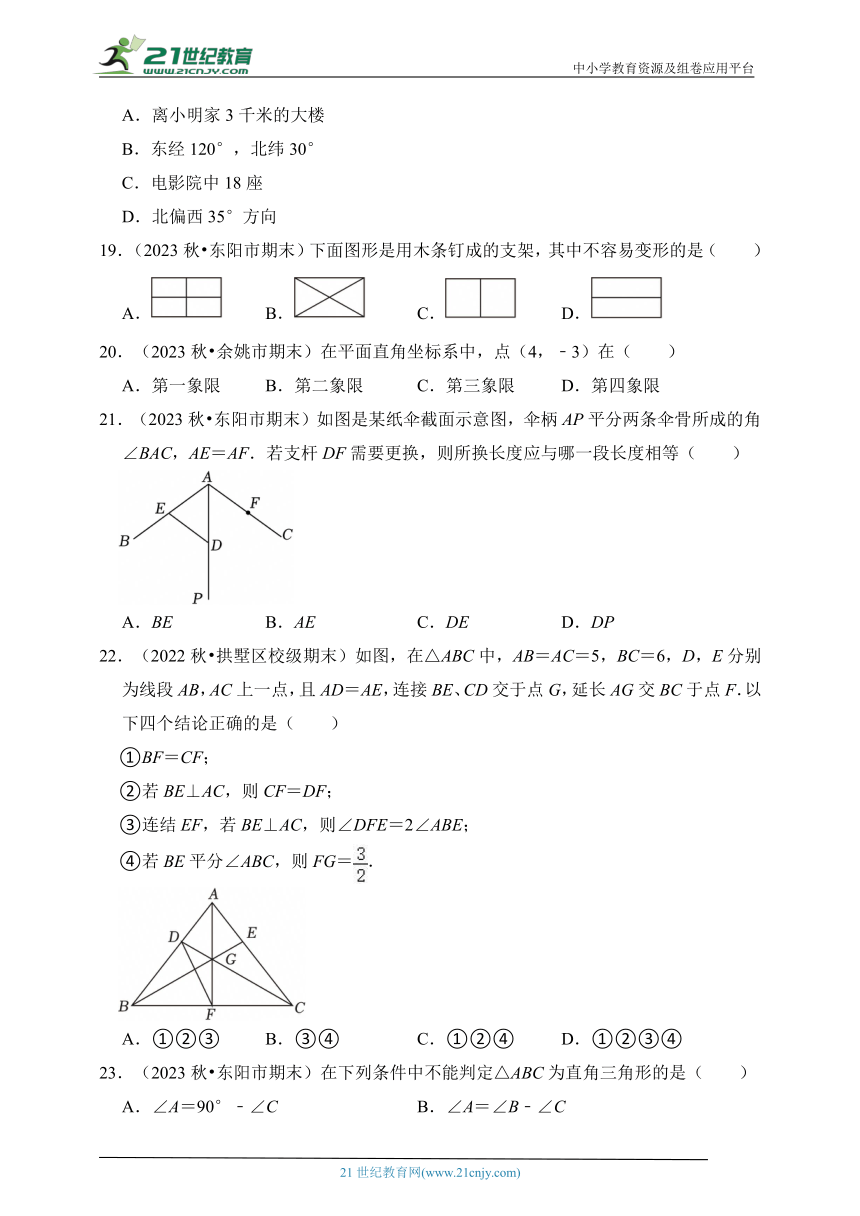
18.(2023秋 武义县期末)下列说法中,能确定物体位置的是( )
A.离小明家3千米的大楼
B.东经120°,北纬30°
C.电影院中18座
D.北偏西35°方向
19.(2023秋 东阳市期末)下面图形是用木条钉成的支架,其中不容易变形的是( )
A. B. C. D.
20.(2023秋 余姚市期末)在平面直角坐标系中,点(4,﹣3)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
21.(2023秋 东阳市期末)如图是某纸伞截面示意图,伞柄AP平分两条伞骨所成的角∠BAC,AE=AF.若支杆DF需要更换,则所换长度应与哪一段长度相等( )
A.BE B.AE C.DE D.DP
22.(2022秋 拱墅区校级期末)如图,在△ABC中,AB=AC=5,BC=6,D,E分别为线段AB,AC上一点,且AD=AE,连接BE、CD交于点G,延长AG交BC于点F.以下四个结论正确的是( )
①BF=CF;
②若BE⊥AC,则CF=DF;
③连结EF,若BE⊥AC,则∠DFE=2∠ABE;
④若BE平分∠ABC,则FG=.
A.①②③ B.③④ C.①②④ D.①②③④
23.(2023秋 东阳市期末)在下列条件中不能判定△ABC为直角三角形的是( )
A.∠A=90°﹣∠C B.∠A=∠B﹣∠C
C.∠A=2∠B=3∠C D.∠A=∠B=∠C
24.(2023秋 衢江区期末)在平面直角坐标系中,点(2023,﹣2024)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
25.(2023秋 台州期末)如图,在△ABC中,AB=AC,∠A=32°,以点B为圆心,BC长为半径画弧,交AC于点D,连接BD,则∠ABD的度数是( )
A.42° B.45° C.40° D.35°
26.(2023秋 松阳县期末)围棋起源于中国,古代称之为“弈”,至今已有四千多年的历史.下列由黑、白棋子摆成的图案中,是轴对称图形的是( )
A. B.
C. D.
27.(2023秋 台州期末)在平面直角坐标系中,点(3,﹣2)关于x轴的对称点是( )
A.(3,﹣2) B.(3,2) C.(﹣3,﹣2) D.(﹣3,2)
28.(2023秋 台州期末)已知三角形两边的长分别是3和5,则此三角形第三边的长可能是( )
A.7 B.8 C.9 D.10
29.(2023秋 新昌县期末)一副三角板按如图所示方式叠放在一起,则图中∠α的度数是( )
A.55° B.60° C.65° D.75°
30.(2023秋 宁波期末)下列图形是轴对称图形的有( )
A.2个 B.3个 C.4个 D.5个
31.(2023秋 五峰县期末)下列长度的三条线段,能组成三角形的是( )
A.2cm,3cm,5cm B.2cm,3cm,4cm
C.2cm,2cm,4cm D.1cm,2cm,4cm
32.(2023秋 瓯海区校级期末)在△ABC中,若∠A=22°,∠B=68°,则该三角形是( )
A.直角三角形 B.等边三角形
C.钝角三角形 D.等腰三角形
33.(2023秋 西湖区期末)甲乙两人去超市购物,超市正在举办摸彩活动,单次消费金额每满100元可以拿到1张摸彩券.已知甲一次购买5盒饼干拿到3张摸彩券;乙一次购买5盒饼干与1个蛋糕拿到4张摸彩券,若每盒饼干的售价为x元,每个蛋糕的售价为120元,则x的取值范围是( )
A.56≤x<76 B.56≤x<80 C.60≤x<76 D.60≤x<80
34.(2023秋 西湖区期末)下列选项中,能说明命题“对于任何实数a,都有a2>a”是假命题的a的值可以是( )
A.﹣2 B.0 C.2 D.4
35.(2023秋 婺城区期末)已知一个等腰三角形的周长为10,腰长为4,则它的底边长为( )
A.2 B.3 C.4 D.6
36.(2023秋 裕安区校级期末)一次函数y=kx+b与正比例函数y=kbx,k,b是常数,且kb≠0的图象可能是( )
A. B.
C. D.
37.(2023秋 鄞州区期末)若关于x的不等式组的整数解共有6个,则a的取值范围是( )
A.﹣5<a<﹣4 B.﹣5<a≤﹣4 C.﹣5≤a<﹣4 D.﹣5≤a≤﹣4
38.(2023秋 长兴县期末)如图,已知点F在BC上,且△ABC≌△AEF,有同学在推出AB=AE,∠B=∠E后,还分别推出下列结论,其中错误的是( )
A.AC=AF B.∠AFC=∠AFE C.EF=BC D.∠FAB=∠B
39.(2023秋 鄞州区期末)正五角星的对称轴有( )
A.1条 B.3条 C.5条 D.无数条
40.(2023秋 鄞州区期末)如图,AD是△ABC的中线,E,F分别在AB,AC上,且DE⊥DF,则BE+CF与EF的大小关系判断正确的是( )
A.BE+CF<EF B.BE+CF=EF C.BE+CF>EF D.无法确定
41.(2023秋 鄞州区期末)下列命题是真命题的是( )
A.三角形的三条高线相交于三角形内一点
B.三边长为、、的三角形为直角三角形
C.对于任意两个非负实数a、b,有
D.若等腰三角形一边长为2,周长为8,则腰长为3
42.(2023秋 鄞州区期末)已知a是方程x3+2x﹣1=0的一个实数根,则直线y=ax+a﹣1不经过( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
43.(2023秋 滨江区期末)如图,在△ABC中,CA=CB=8,AB=6,∠C<90°,点D,E,F分别在边BC,AC,AB上,连接DF,DE.已知点B和点E关于直线DF对称,若ED=CD,则CE的长为( )
A. B. C. D.
44.(2023秋 长兴县期末)如图所示的网格是由9个相同的小正方形拼成的,图形的各个顶点均为格点,则∠1﹣∠2﹣∠3的度数为( )
A.30° B.45° C.55° D.60°
45.(2023秋 金东区期末)如图,一次函数y=x+m的图象与x轴交于点(﹣3,0),则不等式x+m>0的解为( )
A.x>﹣3 B.x<﹣3 C.x>3 D.x<3
46.(2023秋 义乌市期末)如果把电影票上“4排3座”记作(4,3),那么(5,9)表示( )
A.“5排5座” B.“9排5座” C.“5排9座” D.“9排9座”
47.(2023秋 吴兴区期末)对于命题“若a>b,则a2>b2.”能说明它属于假命题的反例是( )
A.a=2,b=1 B.a=﹣1,b=﹣2 C.a=﹣2,b=﹣1 D.a=3,b=﹣2
48.(2023秋 瓯海区校级期末)如图,在△ABC中,∠C=90°,若AC=1,AB=2,则BC的长是( )
A.1 B. C.2 D.
49.(2023秋 金东区期末)如图,是由四个全等的直角三角形拼成的“赵爽弦图”,得到正方形ABCD与正方形EFGH,连结DF.若S正方形ABCD=5,EF=BG,则DF的长为( )
A.2 B. C.3 D.
50.(2023秋 镇海区校级期末)使有意义的x的取值范围是( )
A.x>2024 B.x<﹣2024 C.x≤2024 D.x≥2024
51.(2023秋 海曙区校级期末)将一副三角板按如图所示的方式放置,图中∠CAF的大小等于( )
A.50° B.60° C.75° D.85°
52.(2023秋 瓯海区校级期末)下面四个图形中,线段BD是△ABC的高的是( )
A. B.
C. D.
53.(2023秋 南浔区期末)在△ABC中,∠B=35°,∠C=50°,分别以点A、C为圆心,大于的长为半径画弧,过两弧的交点作直线,交BC于点P,连结AP,则∠BAP的度数是( )
A.35° B.40° C.45° D.50°
54.(2023秋 南浔区期末)如图,小明书上的三角形被墨迹污染了一部分,很快他就根据所学知识画出一个与书上完全一样的三角形,那么这两个三角形完全一样的依据是( )
A.SSS B.SAS C.SSA D.ASA
55.(2023秋 北仑区期末)若x<y,则( )
A.x+1>y+1 B.x﹣1>y﹣1 C.2x>2y D.
56.(2023秋 滨江区期末)等腰三角形的一个外角是80°,则其底角等于( )
A.40° B.80° C.100° D.40°或100°
57.(2023秋 江北区期末)将x2+4x+2=0左边配成完全平方后,得方程( )
A.(x+4)2=2 B.(x+2)2=2 C.(x+2)2=4 D.(x+4)2=4
58.(2023秋 开化县期末)如图,小筧家里有一块三角形玻璃碎了,他带着残缺的玻璃去玻璃店配一块与原来相同的,请问师傅配出相同玻璃的依据是( )
A.SSS B.SAS C.AAS D.ASA
59.(2023秋 上城区期末)如图,在Rt△ACB中,∠ACB=90°,按下列步骤作图:
①分别以点B,C为圆心,大于的长为半径画弧,两弧相交于点M,N,作直线MN交AB于点D;
②以C为圆心,CD长为半径画弧交AB于点E.
方方探究得到以下两个结论:
①△BCE是等腰△;
②若AC=6,BC=8,则点E到AC的距离为,
则( )
A.结论①正确,结论②正确
B.结论①正确,结论②错误
C.结论①错误,结论②正确
D.结论①错误,结论②错误
60.(2023秋 南浔区期末)2023年第19届亚运会是一场规模盛大的体育盛事,以下是某运会会标,其中是轴对称图形的是( )
A. B.
C. D.
专题01 单选题-2024-2025学年浙江地区八年级数学上学期期末备考真题分类汇编
参考答案与试题解析
题号 1 2 3 4 5 6 7 8 9 10 11
答案 D D D B D C D D A D B
题号 12 13 14 15 16 17 18 19 20 21 22
答案 B C B B B A B B D C D
题号 23 24 25 26 27 28 29 30 31 32 33
答案 C D A D B A D D B A C
题号 34 35 36 37 38 39 40 41 42 43 44
答案 B A C C D C C D B B B
题号 45 46 47 48 49 50 51 52 53 54 55
答案 A C B B B D C D C D D
题号 56 57 58 59 60
答案 A B D C C
一.选择题(共60小题)
1.【答案】D
【解答】解:A、不满足|a|>|b|,不符合题意;
B、条件和结论都与原命题相符,不符合题意;
C、条件和结论都与原命题相符,不符合题意;
D、条件满足|a|>|b|,结论与原命题矛盾,符合题意;
故选:D.
2.【答案】D
【解答】解:人字梯中间一般会设计一“拉杆”,是为了形成三角形,利用三角形具有稳定性来增加其稳定性,
故选:D.
3.【答案】D
【解答】解:令点O和点A旋转后的对应点分别为M和N,
过点M作x轴的垂线,垂足为H,
由旋转可知,
△BMN是等边三角形,且边长为2,
∵MB=MN,MH⊥x轴,
∴BH=,
则OH=2+1=3.
在Rt△MBH中,
MH=,
所以点M的坐标为(3,).
故选:D.
4.【答案】B
【解答】解:∵△ABC≌△DEF,
∴EF=BC=4cm,
∴BE=BF﹣EF=6﹣4=2(cm),
故选:B.
5.【答案】D
【解答】解:A、添加CB=CD,根据SSS,能判定△ABC≌△ADC,故A选项不符合题意;
B、添加∠BAC=∠DAC,根据SAS,能判定△ABC≌△ADC,故B选项不符合题意;
C、添加∠B=∠D=90°,根据HL,能判定△ABC≌△ADC,故C选项不符合题意;
D、添加∠BCA=∠DCA时,不能判定△ABC≌△ADC,故D选项符合题意;
故选:D.
6.【答案】C
【解答】解:A.利用三角形三边对应相等,两三角形全等,三角形形状确定,故此选项不合题意;
B.利用三角形两边、且夹角对应相等,两三角形全等,三角形形状确定,故此选项不合题意;
C.AB,AC,∠B,无法确定三角形的形状,故此选项符合题意;
D.根据∠A,∠B,BC,三角形形状确定,故此选项不合题意;
故选:C.
7.【答案】D
【解答】解:A、B、C选项中的图形都不能找到一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以不是轴对称图形;
D选项中的图形能找到一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以是轴对称图形;
故选:D.
8.【答案】D
【解答】解:A、根据ASA即可证明三角形全等,本选项不符合题意.
B、根据SAS即可证明三角形全等,本选项不符合题意.
C、根据AAS或ASA即可证明三角形全等,本选项不符合题意.
D、SSA不能判定三角形全等,本选项符合题意.
故选:D.
9.【答案】A
【解答】解:点(3,4)的横坐标和纵坐标都大于0,
∴点P(3,4)所在的象限是第一象限,
故选:A.
10.【答案】D
【解答】解:A,B,C选项中的图案都不能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以不是轴对称图形;
D选项中的图案能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以是轴对称图形;
故选:D.
11.【答案】B
【解答】解:∵点C、D处的刻度相同,
∴EC=ED,
∵OE=OE,OC=OD,
∴由SSS判定△ODE≌△OCE.
故选:B.
12.【答案】B
【解答】解:由题意可得点A离数轴上表示2的点的距离为=,
则点A表示的数为:2﹣,
故选:B.
13.【答案】C
【解答】解:∵由图象可知一次函数y=ax+b,y的值随着x值的增大而减小;
故①错误;
∵由图象可知:一次函数y=ax+b与y=mx+n(a<m<0)的图象相交点(﹣3,2),
∴方程组的解为,
故②正确;
∵由图象可知:一次函数y=ax+b与y轴的交点为(0,﹣2),
∴当x=0时,ax+b=﹣2,
故③错误;
∵由图象可知:一次函数y=mx+n(a<m<0)与x轴的交点为(2,0),
∴方程mx+n=0的解为x=2,
故④正确;
∵由图象可知:一次函数y=ax+b图象在y=mx+n(a<m<0)的图象下方的时x≥﹣3,
故⑤正确;
∴正确的有3个;
故选:C.
14.【答案】B
【解答】解:∵点A(﹣3,y1),B(2,y2),C(3,y3)是函数y=﹣x+2图象上的点,
∴y1=3+2=5,y2=﹣2+2=0,y3=﹣3+2=﹣1,
∵5>0>﹣1,
∴y1>y2>y3.
故选:B.
15.【答案】B
【解答】解:,
解不等式得:2<x<a+1,
不等式组有3个整数解,一定是3,4,5.
则5<a+1≤6
解得:4<a≤5.
故选:B.
16.【答案】B
【解答】解:P到三条距离相等,即PD=PE=PF,
连接PA、PB、PC,
∵PD=PE,
∴PB是∠ABC的角平分线,
同理PA、PC分别是∠BAC,∠ACB的角平分线,
故P是△ABC角平分线交点,
故选:B.
17.【答案】A
【解答】解:把x=0代入y=2x﹣3得y=﹣3,
所以直线y=2x﹣3与y轴的交点坐标是(0,﹣3).
故选:A.
18.【答案】B
【解答】解:由题意可得,
离小明家3千米的大楼,可以在一个圆上,不固定,故A不符合题意,
东经120°,北纬30°,能确定位置,故B符合题意,
电影院中18座,没说明哪行的,不固定,故C不符合题意,
北偏西35°方向没说明长度及观测点,不固定,故D不符合题意,
故选:B.
19.【答案】B
【解答】解:含有三角形结构的支架不容易变形.
故选:B.
20.【答案】D
【解答】解:∵4>0,﹣3<0,
∴(4,﹣3)在第四象限.
故选:D.
21.【答案】C
【解答】解:∵AP平分∠BAC.
∴∠EAD=∠FAD,
在△ADE与△ADF中,
,
∴△ADE≌△ADF(SAS),
∴DF=DE,
即所换长度应与DF的长度相等,
故选:C.
22.【答案】D
【解答】解:在△BAE和△CAD中,
,
∴△BAE≌△CAD(SAS),
∴∠ABE=∠ACD,
∵AB=AC=5,
∴∠ABC=∠ACB,
∴∠GBC=∠GCB,
∴BG=CG,
∴点G是BC的中垂线上,
∵AB=AC,
∴点A在BC的中垂线上,
∴AG垂直平分BC,
∴BF=CF,故①正确;
若BE⊥AC,则∠AEB=90°,
∵△BAE≌△CAD,
∴∠ADC=∠AEB=90°,
∴∠BDC=90°,
又∵BF=CF,
∴CF=DF,故②正确;
如图,连接EF,
若BE⊥AC,则∠AEB=90°,
∵△BAE≌△CAD,
∴∠ADC=∠AEB=90°,
∴∠BDC=90°=∠BEC,
又∵BF=CF,
∴CF=DF=EF=BF,
∴∠DBF=∠BDF,∠FEC=∠FCE,
∴2∠DBF+∠DFB=180°,2∠ECF+∠EFC=180°,
又∵∠DFB+∠EFC+∠DFE=180°,
∴2∠DBF+2∠ECF﹣∠DFE=180°,
∵∠BAC+∠ABC+∠ACB=180°,
∴2∠BAC+2∠ABC+2∠ACB=360°,
∴2∠BAC+180°+∠DFE=360°,
∴2∠BAC+∠DFE=180°,
∵∠BAC+∠ABE=90°,
∴∠DFE=2∠ABE,故③正确,
若BE平分∠ABC,
∴∠ABE=∠CBE=∠ABC,
∵∠ABE=∠ACD,∠GBC=∠GCB,
∴∠ACD=∠BCD,
∴点G是角平分线的交点,
∴点G到三边的距离为GF的长,
∵AB=AC=5,BC=6,BF=CF,
∴BF=CF=3,
∴AF===4,
∵S△ABC=×BC AF=×AB GF+×AC GF+×CB GF,
∴FG=,故④正确;
故选:D.
23.【答案】C
【解答】解:A、∵∠A=90°﹣∠C,
∴∠A+∠C=90°,
∴∠B=90°,
∴△ABC是直角三角形,故选项不符合题意;
B、∵∠A=∠B﹣∠C,
∴∠A+∠C=∠B,
∵∠A+∠C+∠B=180°,
∴2∠B=180°,
∴∠B=90°,
∴△ABC是直角三角形,故选项不符合题意;
C、∵∠A=2∠B=3∠C,
设∠A=x,
∴∠B=x,∠C=x,
∵∠A+∠B+∠C=180°,
∴x+x+x=180°,
解得x=()°>90°,
∴△ABC不是直角三角形,故选项符合题意;
D、∵∠A=∠B=∠C,
设∠A=∠B=x,
∴∠C=2x,
∵∠A+∠B+∠C=180°,
∴x+x+2x=180°,
解得x=45°,
∴∠C=2x=90°,
∴△ABC是直角三角形,故选项不符合题意.
故选:C.
24.【答案】D
【解答】解:点(2023,﹣2024)在第四象限,
故选:D.
25.【答案】A
【解答】解:∵AB=AC,∠A=32°,
∴∠ABC=∠ACB=74°,
又∵BC=BD,
∴∠BDC=∠BCD=74°,
∴∠DBC=32°,
∴∠ABD=∠ABC﹣∠DBC=74°﹣32°=42°,
故选:A.
26.【答案】D
【解答】解:∵沿着一条直线折叠,直线两边的部分能完全重合的图形为轴对称图形,
∴为轴对称图形,
故选:D.
27.【答案】B
【解答】解:点(3,﹣2)关于x轴的对称点的坐标为:(3,2).
故选:B.
28.【答案】A
【解答】解:∵三角形两边的长分别是3和5,
∴第三边的取值范围为:5﹣3<第三边<5+3,即2<第三边<8,
∴A符合题意.
故选:A.
29.【答案】D
【解答】解:由题意得:∠1=90°﹣60°=30°,
则∠α=45°+30°=75°,
故选:D.
30.【答案】D
【解答】解:这五个图形都是轴对称图形.
故选:D.
31.【答案】B
【解答】解:A.∵2+3=5,∴不满足三角形三边关系,不能组成三角形,不符合题意;
B.∵4﹣2<3<4+2,∴满足三角形三边关系,能组成三角形,符合题意;
C.∵2+2=4,∴不满足三角形三边关系,不能组成三角形,不符合题意;
D.∵1+2<4,∴不满足三角形三边关系,不能组成三角形,不符合题意.
故选:B.
32.【答案】A
【解答】解:∵∠A+∠B+∠C=180°,
又∵∠A=22°,∠B=68°,
∴∠C=180°﹣22°﹣68°=90°,
∴△ABC是直角三角形,
故选:A.
33.【答案】C
【解答】解:由题意得:,
解得:60≤x<76,
故选:C.
34.【答案】B
【解答】解:A、当a=﹣2时,a2=4,
∴a2>a,不符合题意;
B、当a=0时,a2=0,
∴a2=a,符合题意;
C、当a=2时,a2=4,
∴a2>a,不符合题意;
D、当a=4时,a2=16,
∴a2>a,不符合题意;
故选:B.
35.【答案】A
【解答】解:因为等腰三角形的周长为10,其腰长为4,
所以它的底边长为10﹣4﹣4=2.
故选:A.
36.【答案】C
【解答】解:根据一次函数的图象分析可得:
A、由一次函数y=kx+b图象可知k<0,b>0;即kb<0,与正比例函数y=kbx的图象可知kb<0,矛盾,故此选项不可能;
B、由一次函数y=kx+b图象可知k>0,b<0;即kb<0,与正比例函数y=kbx的图象可知kb>0,矛盾,故此选项不可能;
C、由一次函数y=kx+b图象可知k>0,b<0;即kb<0,与正比例函数y=kbx的图象可知kb<0,一致,故此选项有可能;
D、由一次函数y=kx+b图象可知k>0,b>0;即kb>0,与正比例函数y=kbx的图象可知kb<0,矛盾,故此选项不可能;
故选:C.
37.【答案】C
【解答】解:,
解①得:x>a,
解②得:,
∵不等式组的整数解由6个,
∴不等式组的整数解为1,0,﹣1,﹣2,﹣3,﹣4,
∴﹣5≤a<﹣4,
故选:C.
38.【答案】D
【解答】解:∵△ABC≌△AEF,
∴AB=AE,AC=AF,BC=EF,∠B=∠E,∠C=∠AFE,∠CAB=∠FAE,
∴∠AFC=∠AFE,
故选:D.
39.【答案】C
【解答】解:正五角星经过角的顶点和中心点的直线都是它的对称轴,所以有5条对称轴.
故选:C.
40.【答案】C
【解答】解:延长ED至P,使DP=DE,连接FP,CP,
∵AD是△ABC的中线,
∴BD=CD,
在△BDE和△CDP中,
,
∴△BDE≌△CDP(SAS),
∴BE=CP,
∵DE⊥DF,DE=DP,
∴EF=FP,
在△CFP中,CP+CF=BE+CF>FP=EF.
故选:C.
41.【答案】D
【解答】解:直角三角形三条高线相交于直角顶点,故A错误;
∵,故三边长为、、的三角形不是直角三角形,故B错误;
对于任意两个非负实数a、b,有,故C错误;
若等腰三角形一边长为2,周长为8,此时三边长可能为2,2,4或3,3,2,根据三角形边长关系,2,2,4无法组成三角形,故等腰三角形的腰长为3,故D正确,
故选:D.
42.【答案】B
【解答】解:由a是方程x3+2x﹣1=0的一个实数根,则有a3+2a﹣1=0,显然a≠0,
通过变形得a(a2+2)=1,
因为a2+2>2,
所以,
∴,
故y=ax+a﹣1随着x的增大而增大,且交y轴于负半轴,故不经过第二象限,
故选:B.
43.【答案】B
【解答】解:如图,连接EB,过点C作CJ⊥AB于点J.
∵B,E关于DF对称,
∴DB=DE,
∵ED=DC,
∴DB=DE=DC,
∴∠BEC=90°,
∴BE⊥AC,
∵CA=CB=8,CJ⊥AB,
∴AJ=JB=AB=3,
∴CJ===,
∴S△ABC= AB CJ= AC BE,
∴BE==,
∴CE===.
故选:B.
44.【答案】B
【解答】解:如图,则∠1=90°,∠2=∠4,∠3+∠4=45°,
∴∠1﹣∠2﹣∠3=90°﹣45°=45°,
故选:B.
45.【答案】A
【解答】解:∵一次函数y=x+m的图象与x轴交于点(﹣3,0),且y随x的增大而增大,
当x>﹣3时,y>0,即x+m>0,
∴不等式x+m>0的解为x>﹣3.
故选:A.
46.【答案】C
【解答】解:由题意知,(5,9)表示“5排9座”,
故选:C.
47.【答案】B
【解答】解:对于命题“若a>b,则a2>b2”,能说明它属于假命题的反例是a=﹣1,b=﹣2,a>b,但(﹣1)2<(﹣2)2,
故选:B.
48.【答案】B
【解答】解:∵∠C=90°,AC=1,AB=2,
∴BC===,
即BC的长是,
故选:B.
49.【答案】B
【解答】解:∵S正方形ABCD=5,四边形ABCD为正方形,
∴AD=AB=BC=CD=.
∵四边形EFGH为正方形,
∴EH=EF=FG=HG.
由题可知:△ADE≌△ABF≌△BCG≌△CDH.
∵EF=BG,
∴EF=AF,
∴E是中点,
即AE=EF,
∴.
∴△ADE≌△DEF(SAS).
即DF=AD=.
故选:B.
50.【答案】D
【解答】解:由题可知,
x﹣2024≥0,
解得x≥2024.
故选:D.
51.【答案】C
【解答】解:∵∠DAC=∠DFE+∠C=60°+45°=105°,
∴∠CAF=180°﹣∠DAC=75°,
故选:C.
52.【答案】D
【解答】解:由图可得,线段BD是△ABC的高的图是D选项.
故选:D.
53.【答案】C
【解答】解:在△ABC中,∠B=35°,∠C=50°,
则∠BAC=180°﹣∠B﹣∠C=95°,
根据线段垂直平分线的性质,得PA=PC,
∴∠PAC=∠C=50°,
∴∠BAP=∠BAC﹣∠PAC=95°﹣50°=45°,
故选:C.
54.【答案】D
【解答】解:由图可知,三角形两角及夹边可以作出,
所以,依据是ASA.
故选:D.
55.【答案】D
【解答】解:∵x<y,
∴x+1<y+1,
∴选项A不符合题意;
∵x<y,
∴x﹣1<y﹣1,
∴选项B不符合题意;
∵x<y,
∴2x<2y,
∴选项C不符合题意;
∵x<y,
∴﹣>﹣,
∴选项D符合题意.
故选:D.
56.【答案】A
【解答】解:∵等腰三角形的一个外角为80°,
∴相邻角为180°﹣80°=100°,
∵三角形的底角不能为钝角,
∴100°角为顶角,
∴底角为:(180°﹣100°)÷2=40°.
故答案为:A.
57.【答案】B
【解答】解:x2+4x+2=0,
x2+4x=﹣2,
x2+4x+4=﹣2+4,
(x+2)2=2,
故选:B.
58.【答案】D
【解答】解:这片碎玻璃的两个角和这两个角所夹的边确定,从而可根据“ASA”重新配一块与原来全等的三角形玻璃.
故选:D.
59.【答案】C
【解答】解:①错误.当∠B=30°时,E,A重合,△BCE明显不是等腰三角形;
②正确.
理由:过点C作CH⊥AB于点H,过点E作EG⊥AC于点G.
∵AC=6,BC=8,∠ACB=90°,
∴AB===10,
∴CH===,
∴AH===,
由作图可知DA=DC=DB=5,
∵CE=CD=5,
∴EH===,
∴AE=AH=EH=﹣=,
∵S△ACE= AC EG= AE CH,
∴EG=,故②正确.
故选:C.
60.【答案】C
【解答】解:A、图形不是轴对称图形,不符合题意;
B、图形不是轴对称图形,不符合题意;
C、图形是轴对称图形,符合题意;
D、图形不是轴对称图形,不符合题意,
故选:C.
声明:试题解析著作
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
专题01 单选题
一.选择题(共60小题)
1.(2023秋 衢州期末)要说明命题“若|a|>|b|,则a>b”是假命题,能举的一个反例是( )
A.a=1,b=﹣2 B.a=2,b=1 C.a=4,b=﹣1 D.a=﹣3,b=﹣2
2.(2023秋 义乌市期末)人字梯中间一般会设计一“拉杆”,这样做的道理是( )
A.两点之间,线段最短
B.垂线段最短
C.两直线平行,内错角相等
D.三角形具有稳定性
3.(2023秋 金东区期末)如图,在直角坐标系中,正△OAB的边OB在x轴的正半轴上,若OA=2,则正△OAB绕着点B顺时针旋转120°后,点O的对应点坐标是( )
A.(2,0) B.(4,0) C. D.
4.(2024秋 江岸区校级期末)如图,△ABC≌△DEF,边BC和EF在同一条直线上.若BC=4cm,BF=6cm,则BE长为( )
A.1cm B.2cm C.3cm D.4cm
5.(2023秋 鄞州区期末)如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )
A.CB=CD B.∠BAC=∠DAC C.∠B=∠D=90° D.∠BCA=∠DCA
6.(2023秋 武义县期末)如图,小明家仿古家具的一块三角形形状的玻璃坏了,需要重新配一块,小明通过电话给玻璃店老板提供相关数据,为了方便表述,将该三角形记为△ABC,提供了下列各组元素的数据,配出来的玻璃不一定符合要求的是( )
A.AB,BC,AC B.AB,BC,∠B C.AB,AC,∠B D.∠A,∠B,BC
7.(2024秋 丰南区期中)下列图形是轴对称图形的为( )
A. B.
C. D.
8.(2023秋 余姚市期末)如图,AB=AC,点D,E分别在AB,AC上,补充下列一个条件后,不能判断△ABE≌△ACD的是( )
A.∠B=∠C B.AD=AE C.∠BDC=∠CEB D.BE=CD
9.(2023秋 吴兴区期末)在平面直角坐标系中,点P(3,4)所在的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
10.(2023秋 鄞州区校级期末)围棋起源于中国,古代称之为“弈”,至今已有四千多年的历史,下列由黑白棋子摆成的图案是轴对称图形的是( )
A. B.
C. D.
11.(2023秋 海曙区期末)工人师傅常借助“角尺”这个工具来平分一个角,其背后的依据就是全等三角形的性质.如图,在∠AOB的两边OA、OB上分别取OC=OD,适当摆放角尺(图中的∠CED),使其两边分别经过点C、D,且点C、D处的刻度相同,这时经过角尺顶点E的射线OE就是∠AOB的平分线.这里判定两个三角形全等的依据是( )
A.SAS B.SSS C.AAS D.ASA
12.(2023秋 玉环市期末)如图,以数轴的单位长度线段为边作一个正方形,以表示数2的点为圆心,正方形对角线长为半径画半圆,交数轴于点A和点B,则点A表示的数是( )
A. B. C. D.
13.(2023秋 鄞州区校级期末)如图,在同一平面直角坐标系中,一次函数y=ax+b与y=mx+n(a<m<0)的图象如图所示,小星根据图象得到如下结论:
①在一次函数y=ax+b的图象中,y的值随着x值的增大而增大;
②方程组的解为,
③当x=0时,ax+b=﹣1;
④方程mx+n=0的解为x=2;
⑤不等式mx+n≥ax+b的解集是x≥﹣3.
其中结论正确的个数是( )
A.1 B.2 C.3 D.4
14.(2023秋 鄞州区期末)若点A(﹣3,y1),B(2,y2),C(3,y3)是函数y=﹣x+2图象上的点,则( )
A.y1<y2<y3 B.y1>y2>y3 C.y1<y3<y2 D.y2>y3>y1
15.(2023秋 滨江区校级期末)不等式组有3个整数解,则a的取值范围是( )
A.5<a≤6 B.4<a≤5 C.4≤a<5 D.5≤a<6
16.(2023秋 台州期末)P是△ABC内一点,PD⊥BC,PE⊥AB,PF⊥AC,垂足分别为D,E,F,且PD=PE=PF,则点P是△ABC( )
A.三边垂直平分线的交点
B.三条角平分线的交点
C.三条高所在直线的交点
D.三条中线的交点
17.(2023秋 宁波期末)在平面直角坐标系中,直线y=2x﹣3与y轴的交点坐标是( )
A.(0,﹣3) B.(﹣3,0) C.(2,﹣3) D.(,0)
18.(2023秋 武义县期末)下列说法中,能确定物体位置的是( )
A.离小明家3千米的大楼
B.东经120°,北纬30°
C.电影院中18座
D.北偏西35°方向
19.(2023秋 东阳市期末)下面图形是用木条钉成的支架,其中不容易变形的是( )
A. B. C. D.
20.(2023秋 余姚市期末)在平面直角坐标系中,点(4,﹣3)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
21.(2023秋 东阳市期末)如图是某纸伞截面示意图,伞柄AP平分两条伞骨所成的角∠BAC,AE=AF.若支杆DF需要更换,则所换长度应与哪一段长度相等( )
A.BE B.AE C.DE D.DP
22.(2022秋 拱墅区校级期末)如图,在△ABC中,AB=AC=5,BC=6,D,E分别为线段AB,AC上一点,且AD=AE,连接BE、CD交于点G,延长AG交BC于点F.以下四个结论正确的是( )
①BF=CF;
②若BE⊥AC,则CF=DF;
③连结EF,若BE⊥AC,则∠DFE=2∠ABE;
④若BE平分∠ABC,则FG=.
A.①②③ B.③④ C.①②④ D.①②③④
23.(2023秋 东阳市期末)在下列条件中不能判定△ABC为直角三角形的是( )
A.∠A=90°﹣∠C B.∠A=∠B﹣∠C
C.∠A=2∠B=3∠C D.∠A=∠B=∠C
24.(2023秋 衢江区期末)在平面直角坐标系中,点(2023,﹣2024)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
25.(2023秋 台州期末)如图,在△ABC中,AB=AC,∠A=32°,以点B为圆心,BC长为半径画弧,交AC于点D,连接BD,则∠ABD的度数是( )
A.42° B.45° C.40° D.35°
26.(2023秋 松阳县期末)围棋起源于中国,古代称之为“弈”,至今已有四千多年的历史.下列由黑、白棋子摆成的图案中,是轴对称图形的是( )
A. B.
C. D.
27.(2023秋 台州期末)在平面直角坐标系中,点(3,﹣2)关于x轴的对称点是( )
A.(3,﹣2) B.(3,2) C.(﹣3,﹣2) D.(﹣3,2)
28.(2023秋 台州期末)已知三角形两边的长分别是3和5,则此三角形第三边的长可能是( )
A.7 B.8 C.9 D.10
29.(2023秋 新昌县期末)一副三角板按如图所示方式叠放在一起,则图中∠α的度数是( )
A.55° B.60° C.65° D.75°
30.(2023秋 宁波期末)下列图形是轴对称图形的有( )
A.2个 B.3个 C.4个 D.5个
31.(2023秋 五峰县期末)下列长度的三条线段,能组成三角形的是( )
A.2cm,3cm,5cm B.2cm,3cm,4cm
C.2cm,2cm,4cm D.1cm,2cm,4cm
32.(2023秋 瓯海区校级期末)在△ABC中,若∠A=22°,∠B=68°,则该三角形是( )
A.直角三角形 B.等边三角形
C.钝角三角形 D.等腰三角形
33.(2023秋 西湖区期末)甲乙两人去超市购物,超市正在举办摸彩活动,单次消费金额每满100元可以拿到1张摸彩券.已知甲一次购买5盒饼干拿到3张摸彩券;乙一次购买5盒饼干与1个蛋糕拿到4张摸彩券,若每盒饼干的售价为x元,每个蛋糕的售价为120元,则x的取值范围是( )
A.56≤x<76 B.56≤x<80 C.60≤x<76 D.60≤x<80
34.(2023秋 西湖区期末)下列选项中,能说明命题“对于任何实数a,都有a2>a”是假命题的a的值可以是( )
A.﹣2 B.0 C.2 D.4
35.(2023秋 婺城区期末)已知一个等腰三角形的周长为10,腰长为4,则它的底边长为( )
A.2 B.3 C.4 D.6
36.(2023秋 裕安区校级期末)一次函数y=kx+b与正比例函数y=kbx,k,b是常数,且kb≠0的图象可能是( )
A. B.
C. D.
37.(2023秋 鄞州区期末)若关于x的不等式组的整数解共有6个,则a的取值范围是( )
A.﹣5<a<﹣4 B.﹣5<a≤﹣4 C.﹣5≤a<﹣4 D.﹣5≤a≤﹣4
38.(2023秋 长兴县期末)如图,已知点F在BC上,且△ABC≌△AEF,有同学在推出AB=AE,∠B=∠E后,还分别推出下列结论,其中错误的是( )
A.AC=AF B.∠AFC=∠AFE C.EF=BC D.∠FAB=∠B
39.(2023秋 鄞州区期末)正五角星的对称轴有( )
A.1条 B.3条 C.5条 D.无数条
40.(2023秋 鄞州区期末)如图,AD是△ABC的中线,E,F分别在AB,AC上,且DE⊥DF,则BE+CF与EF的大小关系判断正确的是( )
A.BE+CF<EF B.BE+CF=EF C.BE+CF>EF D.无法确定
41.(2023秋 鄞州区期末)下列命题是真命题的是( )
A.三角形的三条高线相交于三角形内一点
B.三边长为、、的三角形为直角三角形
C.对于任意两个非负实数a、b,有
D.若等腰三角形一边长为2,周长为8,则腰长为3
42.(2023秋 鄞州区期末)已知a是方程x3+2x﹣1=0的一个实数根,则直线y=ax+a﹣1不经过( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
43.(2023秋 滨江区期末)如图,在△ABC中,CA=CB=8,AB=6,∠C<90°,点D,E,F分别在边BC,AC,AB上,连接DF,DE.已知点B和点E关于直线DF对称,若ED=CD,则CE的长为( )
A. B. C. D.
44.(2023秋 长兴县期末)如图所示的网格是由9个相同的小正方形拼成的,图形的各个顶点均为格点,则∠1﹣∠2﹣∠3的度数为( )
A.30° B.45° C.55° D.60°
45.(2023秋 金东区期末)如图,一次函数y=x+m的图象与x轴交于点(﹣3,0),则不等式x+m>0的解为( )
A.x>﹣3 B.x<﹣3 C.x>3 D.x<3
46.(2023秋 义乌市期末)如果把电影票上“4排3座”记作(4,3),那么(5,9)表示( )
A.“5排5座” B.“9排5座” C.“5排9座” D.“9排9座”
47.(2023秋 吴兴区期末)对于命题“若a>b,则a2>b2.”能说明它属于假命题的反例是( )
A.a=2,b=1 B.a=﹣1,b=﹣2 C.a=﹣2,b=﹣1 D.a=3,b=﹣2
48.(2023秋 瓯海区校级期末)如图,在△ABC中,∠C=90°,若AC=1,AB=2,则BC的长是( )
A.1 B. C.2 D.
49.(2023秋 金东区期末)如图,是由四个全等的直角三角形拼成的“赵爽弦图”,得到正方形ABCD与正方形EFGH,连结DF.若S正方形ABCD=5,EF=BG,则DF的长为( )
A.2 B. C.3 D.
50.(2023秋 镇海区校级期末)使有意义的x的取值范围是( )
A.x>2024 B.x<﹣2024 C.x≤2024 D.x≥2024
51.(2023秋 海曙区校级期末)将一副三角板按如图所示的方式放置,图中∠CAF的大小等于( )
A.50° B.60° C.75° D.85°
52.(2023秋 瓯海区校级期末)下面四个图形中,线段BD是△ABC的高的是( )
A. B.
C. D.
53.(2023秋 南浔区期末)在△ABC中,∠B=35°,∠C=50°,分别以点A、C为圆心,大于的长为半径画弧,过两弧的交点作直线,交BC于点P,连结AP,则∠BAP的度数是( )
A.35° B.40° C.45° D.50°
54.(2023秋 南浔区期末)如图,小明书上的三角形被墨迹污染了一部分,很快他就根据所学知识画出一个与书上完全一样的三角形,那么这两个三角形完全一样的依据是( )
A.SSS B.SAS C.SSA D.ASA
55.(2023秋 北仑区期末)若x<y,则( )
A.x+1>y+1 B.x﹣1>y﹣1 C.2x>2y D.
56.(2023秋 滨江区期末)等腰三角形的一个外角是80°,则其底角等于( )
A.40° B.80° C.100° D.40°或100°
57.(2023秋 江北区期末)将x2+4x+2=0左边配成完全平方后,得方程( )
A.(x+4)2=2 B.(x+2)2=2 C.(x+2)2=4 D.(x+4)2=4
58.(2023秋 开化县期末)如图,小筧家里有一块三角形玻璃碎了,他带着残缺的玻璃去玻璃店配一块与原来相同的,请问师傅配出相同玻璃的依据是( )
A.SSS B.SAS C.AAS D.ASA
59.(2023秋 上城区期末)如图,在Rt△ACB中,∠ACB=90°,按下列步骤作图:
①分别以点B,C为圆心,大于的长为半径画弧,两弧相交于点M,N,作直线MN交AB于点D;
②以C为圆心,CD长为半径画弧交AB于点E.
方方探究得到以下两个结论:
①△BCE是等腰△;
②若AC=6,BC=8,则点E到AC的距离为,
则( )
A.结论①正确,结论②正确
B.结论①正确,结论②错误
C.结论①错误,结论②正确
D.结论①错误,结论②错误
60.(2023秋 南浔区期末)2023年第19届亚运会是一场规模盛大的体育盛事,以下是某运会会标,其中是轴对称图形的是( )
A. B.
C. D.
专题01 单选题-2024-2025学年浙江地区八年级数学上学期期末备考真题分类汇编
参考答案与试题解析
题号 1 2 3 4 5 6 7 8 9 10 11
答案 D D D B D C D D A D B
题号 12 13 14 15 16 17 18 19 20 21 22
答案 B C B B B A B B D C D
题号 23 24 25 26 27 28 29 30 31 32 33
答案 C D A D B A D D B A C
题号 34 35 36 37 38 39 40 41 42 43 44
答案 B A C C D C C D B B B
题号 45 46 47 48 49 50 51 52 53 54 55
答案 A C B B B D C D C D D
题号 56 57 58 59 60
答案 A B D C C
一.选择题(共60小题)
1.【答案】D
【解答】解:A、不满足|a|>|b|,不符合题意;
B、条件和结论都与原命题相符,不符合题意;
C、条件和结论都与原命题相符,不符合题意;
D、条件满足|a|>|b|,结论与原命题矛盾,符合题意;
故选:D.
2.【答案】D
【解答】解:人字梯中间一般会设计一“拉杆”,是为了形成三角形,利用三角形具有稳定性来增加其稳定性,
故选:D.
3.【答案】D
【解答】解:令点O和点A旋转后的对应点分别为M和N,
过点M作x轴的垂线,垂足为H,
由旋转可知,
△BMN是等边三角形,且边长为2,
∵MB=MN,MH⊥x轴,
∴BH=,
则OH=2+1=3.
在Rt△MBH中,
MH=,
所以点M的坐标为(3,).
故选:D.
4.【答案】B
【解答】解:∵△ABC≌△DEF,
∴EF=BC=4cm,
∴BE=BF﹣EF=6﹣4=2(cm),
故选:B.
5.【答案】D
【解答】解:A、添加CB=CD,根据SSS,能判定△ABC≌△ADC,故A选项不符合题意;
B、添加∠BAC=∠DAC,根据SAS,能判定△ABC≌△ADC,故B选项不符合题意;
C、添加∠B=∠D=90°,根据HL,能判定△ABC≌△ADC,故C选项不符合题意;
D、添加∠BCA=∠DCA时,不能判定△ABC≌△ADC,故D选项符合题意;
故选:D.
6.【答案】C
【解答】解:A.利用三角形三边对应相等,两三角形全等,三角形形状确定,故此选项不合题意;
B.利用三角形两边、且夹角对应相等,两三角形全等,三角形形状确定,故此选项不合题意;
C.AB,AC,∠B,无法确定三角形的形状,故此选项符合题意;
D.根据∠A,∠B,BC,三角形形状确定,故此选项不合题意;
故选:C.
7.【答案】D
【解答】解:A、B、C选项中的图形都不能找到一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以不是轴对称图形;
D选项中的图形能找到一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以是轴对称图形;
故选:D.
8.【答案】D
【解答】解:A、根据ASA即可证明三角形全等,本选项不符合题意.
B、根据SAS即可证明三角形全等,本选项不符合题意.
C、根据AAS或ASA即可证明三角形全等,本选项不符合题意.
D、SSA不能判定三角形全等,本选项符合题意.
故选:D.
9.【答案】A
【解答】解:点(3,4)的横坐标和纵坐标都大于0,
∴点P(3,4)所在的象限是第一象限,
故选:A.
10.【答案】D
【解答】解:A,B,C选项中的图案都不能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以不是轴对称图形;
D选项中的图案能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以是轴对称图形;
故选:D.
11.【答案】B
【解答】解:∵点C、D处的刻度相同,
∴EC=ED,
∵OE=OE,OC=OD,
∴由SSS判定△ODE≌△OCE.
故选:B.
12.【答案】B
【解答】解:由题意可得点A离数轴上表示2的点的距离为=,
则点A表示的数为:2﹣,
故选:B.
13.【答案】C
【解答】解:∵由图象可知一次函数y=ax+b,y的值随着x值的增大而减小;
故①错误;
∵由图象可知:一次函数y=ax+b与y=mx+n(a<m<0)的图象相交点(﹣3,2),
∴方程组的解为,
故②正确;
∵由图象可知:一次函数y=ax+b与y轴的交点为(0,﹣2),
∴当x=0时,ax+b=﹣2,
故③错误;
∵由图象可知:一次函数y=mx+n(a<m<0)与x轴的交点为(2,0),
∴方程mx+n=0的解为x=2,
故④正确;
∵由图象可知:一次函数y=ax+b图象在y=mx+n(a<m<0)的图象下方的时x≥﹣3,
故⑤正确;
∴正确的有3个;
故选:C.
14.【答案】B
【解答】解:∵点A(﹣3,y1),B(2,y2),C(3,y3)是函数y=﹣x+2图象上的点,
∴y1=3+2=5,y2=﹣2+2=0,y3=﹣3+2=﹣1,
∵5>0>﹣1,
∴y1>y2>y3.
故选:B.
15.【答案】B
【解答】解:,
解不等式得:2<x<a+1,
不等式组有3个整数解,一定是3,4,5.
则5<a+1≤6
解得:4<a≤5.
故选:B.
16.【答案】B
【解答】解:P到三条距离相等,即PD=PE=PF,
连接PA、PB、PC,
∵PD=PE,
∴PB是∠ABC的角平分线,
同理PA、PC分别是∠BAC,∠ACB的角平分线,
故P是△ABC角平分线交点,
故选:B.
17.【答案】A
【解答】解:把x=0代入y=2x﹣3得y=﹣3,
所以直线y=2x﹣3与y轴的交点坐标是(0,﹣3).
故选:A.
18.【答案】B
【解答】解:由题意可得,
离小明家3千米的大楼,可以在一个圆上,不固定,故A不符合题意,
东经120°,北纬30°,能确定位置,故B符合题意,
电影院中18座,没说明哪行的,不固定,故C不符合题意,
北偏西35°方向没说明长度及观测点,不固定,故D不符合题意,
故选:B.
19.【答案】B
【解答】解:含有三角形结构的支架不容易变形.
故选:B.
20.【答案】D
【解答】解:∵4>0,﹣3<0,
∴(4,﹣3)在第四象限.
故选:D.
21.【答案】C
【解答】解:∵AP平分∠BAC.
∴∠EAD=∠FAD,
在△ADE与△ADF中,
,
∴△ADE≌△ADF(SAS),
∴DF=DE,
即所换长度应与DF的长度相等,
故选:C.
22.【答案】D
【解答】解:在△BAE和△CAD中,
,
∴△BAE≌△CAD(SAS),
∴∠ABE=∠ACD,
∵AB=AC=5,
∴∠ABC=∠ACB,
∴∠GBC=∠GCB,
∴BG=CG,
∴点G是BC的中垂线上,
∵AB=AC,
∴点A在BC的中垂线上,
∴AG垂直平分BC,
∴BF=CF,故①正确;
若BE⊥AC,则∠AEB=90°,
∵△BAE≌△CAD,
∴∠ADC=∠AEB=90°,
∴∠BDC=90°,
又∵BF=CF,
∴CF=DF,故②正确;
如图,连接EF,
若BE⊥AC,则∠AEB=90°,
∵△BAE≌△CAD,
∴∠ADC=∠AEB=90°,
∴∠BDC=90°=∠BEC,
又∵BF=CF,
∴CF=DF=EF=BF,
∴∠DBF=∠BDF,∠FEC=∠FCE,
∴2∠DBF+∠DFB=180°,2∠ECF+∠EFC=180°,
又∵∠DFB+∠EFC+∠DFE=180°,
∴2∠DBF+2∠ECF﹣∠DFE=180°,
∵∠BAC+∠ABC+∠ACB=180°,
∴2∠BAC+2∠ABC+2∠ACB=360°,
∴2∠BAC+180°+∠DFE=360°,
∴2∠BAC+∠DFE=180°,
∵∠BAC+∠ABE=90°,
∴∠DFE=2∠ABE,故③正确,
若BE平分∠ABC,
∴∠ABE=∠CBE=∠ABC,
∵∠ABE=∠ACD,∠GBC=∠GCB,
∴∠ACD=∠BCD,
∴点G是角平分线的交点,
∴点G到三边的距离为GF的长,
∵AB=AC=5,BC=6,BF=CF,
∴BF=CF=3,
∴AF===4,
∵S△ABC=×BC AF=×AB GF+×AC GF+×CB GF,
∴FG=,故④正确;
故选:D.
23.【答案】C
【解答】解:A、∵∠A=90°﹣∠C,
∴∠A+∠C=90°,
∴∠B=90°,
∴△ABC是直角三角形,故选项不符合题意;
B、∵∠A=∠B﹣∠C,
∴∠A+∠C=∠B,
∵∠A+∠C+∠B=180°,
∴2∠B=180°,
∴∠B=90°,
∴△ABC是直角三角形,故选项不符合题意;
C、∵∠A=2∠B=3∠C,
设∠A=x,
∴∠B=x,∠C=x,
∵∠A+∠B+∠C=180°,
∴x+x+x=180°,
解得x=()°>90°,
∴△ABC不是直角三角形,故选项符合题意;
D、∵∠A=∠B=∠C,
设∠A=∠B=x,
∴∠C=2x,
∵∠A+∠B+∠C=180°,
∴x+x+2x=180°,
解得x=45°,
∴∠C=2x=90°,
∴△ABC是直角三角形,故选项不符合题意.
故选:C.
24.【答案】D
【解答】解:点(2023,﹣2024)在第四象限,
故选:D.
25.【答案】A
【解答】解:∵AB=AC,∠A=32°,
∴∠ABC=∠ACB=74°,
又∵BC=BD,
∴∠BDC=∠BCD=74°,
∴∠DBC=32°,
∴∠ABD=∠ABC﹣∠DBC=74°﹣32°=42°,
故选:A.
26.【答案】D
【解答】解:∵沿着一条直线折叠,直线两边的部分能完全重合的图形为轴对称图形,
∴为轴对称图形,
故选:D.
27.【答案】B
【解答】解:点(3,﹣2)关于x轴的对称点的坐标为:(3,2).
故选:B.
28.【答案】A
【解答】解:∵三角形两边的长分别是3和5,
∴第三边的取值范围为:5﹣3<第三边<5+3,即2<第三边<8,
∴A符合题意.
故选:A.
29.【答案】D
【解答】解:由题意得:∠1=90°﹣60°=30°,
则∠α=45°+30°=75°,
故选:D.
30.【答案】D
【解答】解:这五个图形都是轴对称图形.
故选:D.
31.【答案】B
【解答】解:A.∵2+3=5,∴不满足三角形三边关系,不能组成三角形,不符合题意;
B.∵4﹣2<3<4+2,∴满足三角形三边关系,能组成三角形,符合题意;
C.∵2+2=4,∴不满足三角形三边关系,不能组成三角形,不符合题意;
D.∵1+2<4,∴不满足三角形三边关系,不能组成三角形,不符合题意.
故选:B.
32.【答案】A
【解答】解:∵∠A+∠B+∠C=180°,
又∵∠A=22°,∠B=68°,
∴∠C=180°﹣22°﹣68°=90°,
∴△ABC是直角三角形,
故选:A.
33.【答案】C
【解答】解:由题意得:,
解得:60≤x<76,
故选:C.
34.【答案】B
【解答】解:A、当a=﹣2时,a2=4,
∴a2>a,不符合题意;
B、当a=0时,a2=0,
∴a2=a,符合题意;
C、当a=2时,a2=4,
∴a2>a,不符合题意;
D、当a=4时,a2=16,
∴a2>a,不符合题意;
故选:B.
35.【答案】A
【解答】解:因为等腰三角形的周长为10,其腰长为4,
所以它的底边长为10﹣4﹣4=2.
故选:A.
36.【答案】C
【解答】解:根据一次函数的图象分析可得:
A、由一次函数y=kx+b图象可知k<0,b>0;即kb<0,与正比例函数y=kbx的图象可知kb<0,矛盾,故此选项不可能;
B、由一次函数y=kx+b图象可知k>0,b<0;即kb<0,与正比例函数y=kbx的图象可知kb>0,矛盾,故此选项不可能;
C、由一次函数y=kx+b图象可知k>0,b<0;即kb<0,与正比例函数y=kbx的图象可知kb<0,一致,故此选项有可能;
D、由一次函数y=kx+b图象可知k>0,b>0;即kb>0,与正比例函数y=kbx的图象可知kb<0,矛盾,故此选项不可能;
故选:C.
37.【答案】C
【解答】解:,
解①得:x>a,
解②得:,
∵不等式组的整数解由6个,
∴不等式组的整数解为1,0,﹣1,﹣2,﹣3,﹣4,
∴﹣5≤a<﹣4,
故选:C.
38.【答案】D
【解答】解:∵△ABC≌△AEF,
∴AB=AE,AC=AF,BC=EF,∠B=∠E,∠C=∠AFE,∠CAB=∠FAE,
∴∠AFC=∠AFE,
故选:D.
39.【答案】C
【解答】解:正五角星经过角的顶点和中心点的直线都是它的对称轴,所以有5条对称轴.
故选:C.
40.【答案】C
【解答】解:延长ED至P,使DP=DE,连接FP,CP,
∵AD是△ABC的中线,
∴BD=CD,
在△BDE和△CDP中,
,
∴△BDE≌△CDP(SAS),
∴BE=CP,
∵DE⊥DF,DE=DP,
∴EF=FP,
在△CFP中,CP+CF=BE+CF>FP=EF.
故选:C.
41.【答案】D
【解答】解:直角三角形三条高线相交于直角顶点,故A错误;
∵,故三边长为、、的三角形不是直角三角形,故B错误;
对于任意两个非负实数a、b,有,故C错误;
若等腰三角形一边长为2,周长为8,此时三边长可能为2,2,4或3,3,2,根据三角形边长关系,2,2,4无法组成三角形,故等腰三角形的腰长为3,故D正确,
故选:D.
42.【答案】B
【解答】解:由a是方程x3+2x﹣1=0的一个实数根,则有a3+2a﹣1=0,显然a≠0,
通过变形得a(a2+2)=1,
因为a2+2>2,
所以,
∴,
故y=ax+a﹣1随着x的增大而增大,且交y轴于负半轴,故不经过第二象限,
故选:B.
43.【答案】B
【解答】解:如图,连接EB,过点C作CJ⊥AB于点J.
∵B,E关于DF对称,
∴DB=DE,
∵ED=DC,
∴DB=DE=DC,
∴∠BEC=90°,
∴BE⊥AC,
∵CA=CB=8,CJ⊥AB,
∴AJ=JB=AB=3,
∴CJ===,
∴S△ABC= AB CJ= AC BE,
∴BE==,
∴CE===.
故选:B.
44.【答案】B
【解答】解:如图,则∠1=90°,∠2=∠4,∠3+∠4=45°,
∴∠1﹣∠2﹣∠3=90°﹣45°=45°,
故选:B.
45.【答案】A
【解答】解:∵一次函数y=x+m的图象与x轴交于点(﹣3,0),且y随x的增大而增大,
当x>﹣3时,y>0,即x+m>0,
∴不等式x+m>0的解为x>﹣3.
故选:A.
46.【答案】C
【解答】解:由题意知,(5,9)表示“5排9座”,
故选:C.
47.【答案】B
【解答】解:对于命题“若a>b,则a2>b2”,能说明它属于假命题的反例是a=﹣1,b=﹣2,a>b,但(﹣1)2<(﹣2)2,
故选:B.
48.【答案】B
【解答】解:∵∠C=90°,AC=1,AB=2,
∴BC===,
即BC的长是,
故选:B.
49.【答案】B
【解答】解:∵S正方形ABCD=5,四边形ABCD为正方形,
∴AD=AB=BC=CD=.
∵四边形EFGH为正方形,
∴EH=EF=FG=HG.
由题可知:△ADE≌△ABF≌△BCG≌△CDH.
∵EF=BG,
∴EF=AF,
∴E是中点,
即AE=EF,
∴.
∴△ADE≌△DEF(SAS).
即DF=AD=.
故选:B.
50.【答案】D
【解答】解:由题可知,
x﹣2024≥0,
解得x≥2024.
故选:D.
51.【答案】C
【解答】解:∵∠DAC=∠DFE+∠C=60°+45°=105°,
∴∠CAF=180°﹣∠DAC=75°,
故选:C.
52.【答案】D
【解答】解:由图可得,线段BD是△ABC的高的图是D选项.
故选:D.
53.【答案】C
【解答】解:在△ABC中,∠B=35°,∠C=50°,
则∠BAC=180°﹣∠B﹣∠C=95°,
根据线段垂直平分线的性质,得PA=PC,
∴∠PAC=∠C=50°,
∴∠BAP=∠BAC﹣∠PAC=95°﹣50°=45°,
故选:C.
54.【答案】D
【解答】解:由图可知,三角形两角及夹边可以作出,
所以,依据是ASA.
故选:D.
55.【答案】D
【解答】解:∵x<y,
∴x+1<y+1,
∴选项A不符合题意;
∵x<y,
∴x﹣1<y﹣1,
∴选项B不符合题意;
∵x<y,
∴2x<2y,
∴选项C不符合题意;
∵x<y,
∴﹣>﹣,
∴选项D符合题意.
故选:D.
56.【答案】A
【解答】解:∵等腰三角形的一个外角为80°,
∴相邻角为180°﹣80°=100°,
∵三角形的底角不能为钝角,
∴100°角为顶角,
∴底角为:(180°﹣100°)÷2=40°.
故答案为:A.
57.【答案】B
【解答】解:x2+4x+2=0,
x2+4x=﹣2,
x2+4x+4=﹣2+4,
(x+2)2=2,
故选:B.
58.【答案】D
【解答】解:这片碎玻璃的两个角和这两个角所夹的边确定,从而可根据“ASA”重新配一块与原来全等的三角形玻璃.
故选:D.
59.【答案】C
【解答】解:①错误.当∠B=30°时,E,A重合,△BCE明显不是等腰三角形;
②正确.
理由:过点C作CH⊥AB于点H,过点E作EG⊥AC于点G.
∵AC=6,BC=8,∠ACB=90°,
∴AB===10,
∴CH===,
∴AH===,
由作图可知DA=DC=DB=5,
∵CE=CD=5,
∴EH===,
∴AE=AH=EH=﹣=,
∵S△ACE= AC EG= AE CH,
∴EG=,故②正确.
故选:C.
60.【答案】C
【解答】解:A、图形不是轴对称图形,不符合题意;
B、图形不是轴对称图形,不符合题意;
C、图形是轴对称图形,符合题意;
D、图形不是轴对称图形,不符合题意,
故选:C.
声明:试题解析著作
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
