专题02 填空题(含解析)-2024-2025学年浙江地区八年级数学上学期期末备考真题分类汇编
文档属性
| 名称 | 专题02 填空题(含解析)-2024-2025学年浙江地区八年级数学上学期期末备考真题分类汇编 |  | |
| 格式 | doc | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-08 08:02:55 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
专题02 填空题
一.填空题(共60小题)
1.(2023秋 台州期末)如图,在△ABC中,∠ABC=90°,∠BAC=40°,点D是△ABC外角∠ACF平分线上的一点,连接AD、BD,若∠ADB=∠ACB,则∠DAC= 度.
2.(2023秋 温岭市期末)已知a+b=5,ab=6.则a2+b2= .
3.(2023秋 义乌市期末)点M(3,﹣1)关于x轴的对称点的坐标为 .
4.(2023秋 瓯海区校级期末)若y﹣1与x+1成正比例,且当x=2时,y=5,则y与x之间的函数表达式为 .
5.(2023秋 柯桥区期末)如图,在Rt△ABC中,∠ABC=90°,点D为AC边上一动点,将△CBD沿着直线BD对折得到△EBD.若∠ABD=15°,则∠ABE的度数为 .
6.(2023秋 瓯海区校级期末)如图的三角形纸片中,AB=8,BC=6,AC=5,沿过点B的直线折叠这个三角形,使点C落在AB边上的点E处,折痕为BD,则△ADE的周长为 .
7.(2023秋 海曙区期末)如图所示,人字梯中间一般会设计一“拉杆”,这样做的依据是 .
8.(2023秋 台州期末)正十边形的每个内角度数为 °.
9.(2023秋 瓯海区校级期末)如图,点P是∠ACB外一点,点D,E分别是CB,CA上的点,点P关于BC的对称点P1落在线段ED的延长线上,点P关于AC的对称点P2恰巧落在ED上.若PE=5,PD=5.5,ED=6.5,则线段P1P2的长为 .
10.(2023秋 海曙区校级期末)若等腰三角形有两条边长分别为2和5,则这个等腰三角形的周长为 .
11.(2023秋 海曙区校级期末)已知,在△ABC中,∠A=∠B+∠C,则△ABC是 三角形.
12.(2023秋 鄞州区期末)方程x2﹣2024x+2023=0的解为 .
13.(2023秋 鄞州区期末)如图,D是△ABC外一点,∠ABC=2∠BAD=90°,BC<AB,AB=2,若,则AC+BD取最小值时,AD﹣BC= .
14.(2023秋 鄞州区期末)在平面直角坐标系中,直线y1=ax+2与y2=bx﹣2交于点(1,﹣1),则不等式的解集为 .
15.(2023秋 舟山期末)根据科学研究表明,10至50岁的人每天所需睡眠时间H(时)可用公式(N是人的年龄).请你用这个公式计算,13岁的小明每天需要睡眠时间 (时).
16.(2023秋 镇海区校级期末)在△ABC中,已知∠A:∠B:∠C=1:3:4,那么△ABC是 三角形(填“锐角”、“直角”或“钝角”).
17.(2023秋 衢江区期末)象棋在中国有着三千多年的历史,老少皆宜.其中棋盘、棋子都蕴含着中国文化,如图,已知“炮”所在位置的坐标为(﹣2,1),“士”所在位置的坐标为(0,﹣2),“相”所在位置的坐标为(3,﹣2),则“马”所在位置的坐标为 .
18.(2023秋 吴兴区期末)已知等腰三角形的顶角等于50°,则底角的度数为 度.
19.(2023秋 瓯海区校级期末)如图所示,A,E,B,D在同一直线上,AB=DE,AC=DF,要使△ABC≌△DEF,需添加的一个条件是 ,并说明理由.
20.(2023秋 莲都区期末)在平面直角坐标系中,点A(2,﹣m+1)与点B(n+1,0)关于y轴对称,则代数式m2+n2的值为 .
21.(2023秋 宁波期末)等腰三角形的一个内角为100°,则它的一个底角的度数为 .
22.(2023秋 莲都区期末)已知直线l1:y=kx+2+k(k≠0)和直线l2:y=x+3.若直线l1、l2与y轴所围成的三角形面积记作S.
(1)当k=﹣1时,S的值是 ;
(2)当2≤S≤3时,k的取值范围是 .
23.(2023秋 瓯海区校级期末)如图,点P是等边△ABC内一点,∠ACP=∠PBC,∠BPC= °.
24.(2023秋 江北区期末)如图,菱形ABCD中,AB=12,∠B=60°,点E是AB上一点,将菱形沿着EC折叠,使点B落在点F处,CF与AD交于点G,点H是EC的中点,,则FG的长为 .
25.(2023秋 江北区期末)已知一次函数y=(a2+1)x﹣3(a为常数,且a≠0)的图象过P(x1,y1),Q(x2,y2)点,若x1>x2,则y1 y2.(用>或<填空)
26.(2023秋 江北区期末)一次函数y=2x﹣2的图象与y轴交点坐标为 .
27.(2023秋 江北区期末)如图,在正方形ABCD中,O为对角线AC,BD的交点,E,F分别为边BC,CD上一点,连接OE,OF,EF,OE⊥OF.若∠AOE=150°,EF=4,则DF的长为 .
28.(2023秋 江北区期末)如图,在平行四边形ABCD中,AE平分∠BAD,E为BC上一点,若CD=4,则BE= .
29.(2023秋 江北区期末)已知关于x的方程x2+(2k+1)x+k2=0的两个实数根的平方和是7,则k= .
30.(2023秋 金东区期末)如图,在数轴上点M、N分别表示数2,﹣2x+1,则x的取值范围是 .
31.(2023秋 武义县期末)若点A(﹣5m,2m﹣1)向上平移3个单位后得到的点在x轴上,则m的值为 .
32.(2023秋 北仑区期末)若直角三角形的两条直角边的长分别是3和4,则斜边上的中线长为 .
33.(2023秋 瓯海区校级期末)“x的3倍与4的差不小于2”用不等式可表示为 .
34.(2023秋 镇海区校级期末)不等式组的解集是x>2,则m的取值范围是 .
35.(2023秋 余姚市期末)一次函数y=(2m﹣6)x+5中,y随x的增大而减小,则m的取值范围是 .
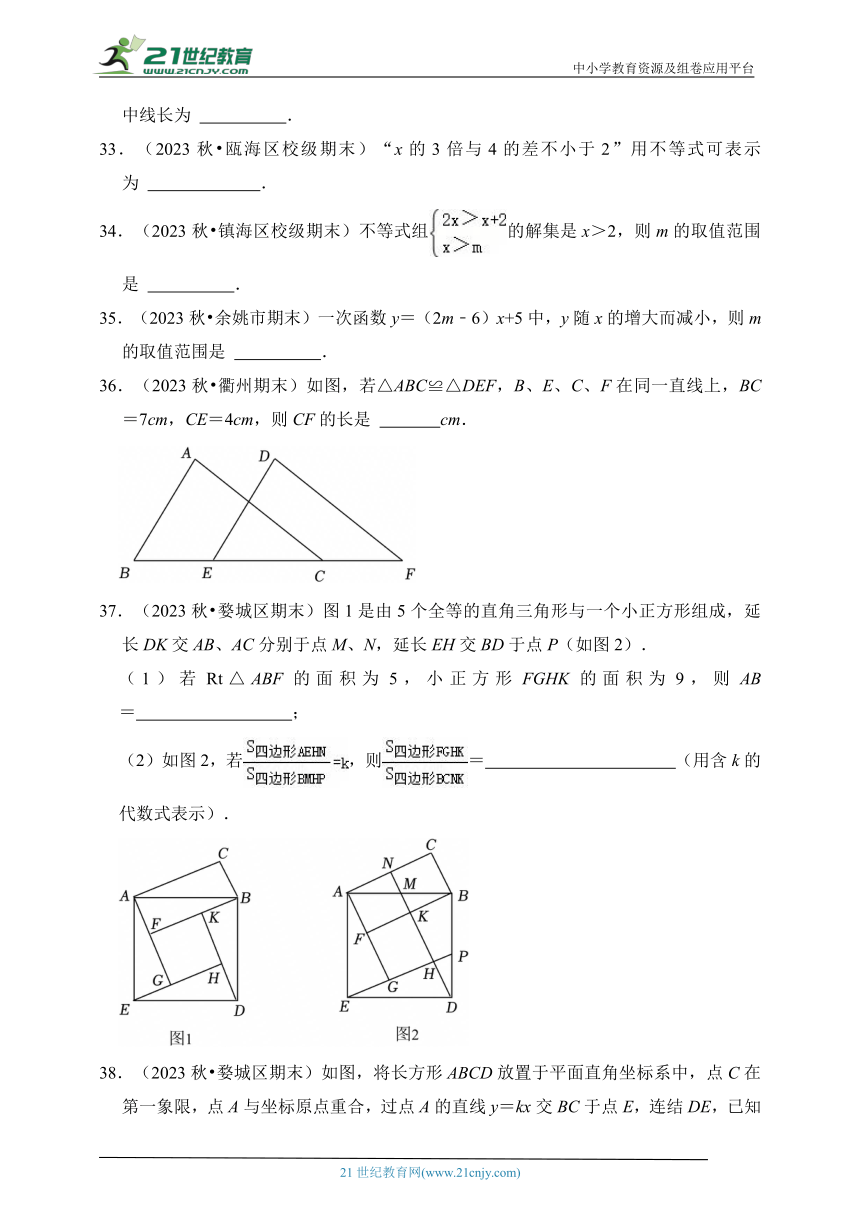
36.(2023秋 衢州期末)如图,若△ABC≌△DEF,B、E、C、F在同一直线上,BC=7cm,CE=4cm,则CF的长是 cm.
37.(2023秋 婺城区期末)图1是由5个全等的直角三角形与一个小正方形组成,延长DK交AB、AC分别于点M、N,延长EH交BD于点P(如图2).
(1)若Rt△ABF的面积为5,小正方形FGHK的面积为9,则AB= ;
(2)如图2,若,则= (用含k的代数式表示).
38.(2023秋 婺城区期末)如图,将长方形ABCD放置于平面直角坐标系中,点C在第一象限,点A与坐标原点重合,过点A的直线y=kx交BC于点E,连结DE,已知BE:CE=1:4,AE平分∠BED,则k的值为 .
39.(2023秋 柯桥区期末)在平面直角坐标系中,点P(﹣2023,2024)在第 象限.
40.(2023秋 浦江县期末)如图,在△ABC中,AD是BC边上的中线,DE⊥AC,DF⊥AB,E,F分别是垂足.已知AB=2AC,则DE与DF的长度之比是 .
41.(2023秋 义乌市期末)若关于x的不等式3x+2≤a的正整数解是1,2,3,4,则整数a的最小值是 .
42.(2023秋 浦江县期末)一次函数y=4x﹣6与x轴的交点坐标为 .
43.(2023秋 浦江县期末)在Rt△ABC中,AB=AC,D,E是斜边BC上的两点,且∠DAE=45°.现将△ADC绕点A旋转90°后得到△AFB,连EF,有下面结论:
①△AED≌△AEF;
②∠FAD=90°;
③BE+CD=DE;
④BE2+CD2=DE2.
其中正确的结论是 .
44.(2023秋 浦江县期末)已知直线与函数的图象相交于A,B两点(点A在点B左侧).
(1)点B的坐标是 .
(2)若坐标原点为点O,将两个函数图象向右平移m个单位,点A,B平移后分别对应点C,D,连接OC,OD,当|OC﹣OD|最大时,m的值为 .
45.(2023秋 鄞州区期末)已知点A(2,m+3),B(n,﹣4)关于y轴对称,则m+n= .
46.(2023秋 金东区期末)如图,在△ABC中,AB>AC,AD、AE分别是△ABC的高线和角平分线,若AD与AE构成的角为∠1=25°,∠B=30°,则∠C= 度.
47.(2023秋 滨江区期末)将“对顶角相等”改写为“如果…那么…”的形式,可写为 .
48.(2023秋 武义县期末)已知A(﹣1,y1),B(﹣0.5,y2),C(1.7,y3),是直线y=﹣9x+b(b为常数)上的三个点,则y1,y2,y3中最小的是 .
49.(2023秋 婺城区期末)剪纸艺术是最古老的中国民间艺术之一,很多剪纸作品体现了数学中的对称美.如图,蝴蝶剪纸是一幅轴对称图形,将其放在平面直角坐标系中,点E的坐标为(﹣2,﹣n),其关于y轴对称的点F的坐标(2,﹣m+1),则(n﹣m)2023= .
50.(2023秋 婺城区期末)在两个全等的三角形中,已知一个三角形的三个内角为30°,α,β(α>β),另一个三角形有一个角为70°,则α﹣β= °.
51.(2023秋 玉环市期末)如图,点O是△ABC内一点,BO平分∠ABC,OD⊥BC于点D,连接OA.若OD=3,AB=10,则△AOB的面积是 .
52.(2023秋 西湖区期末)如图,图中的折线OABC反映了圆圆从家到学校所走的路程S(m)与时间t(min)的函数关系,其中,OA所在直线的表达式为y=k1x(k1≠0),BC所在直线的表达式为y=k2x+b(k2≠0),则k2﹣k1= .
53.(2023秋 舟山期末)已知关于x的一次函数y=(2﹣5a)x+3的图象上有任意两个点(x1,y1),(x2,y2)若(x1﹣x2)(y1﹣y2)<0,则a的取值范围是 .
54.(2023秋 宁波期末)阅读下面材料:在数学课上,老师提出如下问题:
作图:过直线外一点作已知直线的平行线.
已知:直线l及其外一点A(如图1).
求作:l的平行线,使它经过点A.
小凡利用两块形状相同的三角尺进行如下操作:
如图2所示:
(1)用第一块三角尺的一条边贴住直线l,第二块三角尺的一条边紧靠第一块三角尺;
(2)将第二块三角尺沿第一块三角尺移动,使其另一边经过点A,沿这边作出直线AB,所以,直线AB即为所求.
老师说:“小凡的作法正确.”
请回答:小凡的作图依据是 .
55.(2023秋 台州期末)分式方程的解为 .
56.(2023秋 台州期末)分式有意义的条件是 .
57.(2023秋 海曙区校级期末)如图,∠MON=90°,已知△ABC中,AC=BC=25,AB=14,△ABC的顶点A、B分别在边OM、ON上,当点B在边ON上运动时,A随之在OM上运动,△ABC的形状始终保持不变,在运动的过程中,点C到点O的最小距离为 .
58.(2023秋 海曙区校级期末)有一边长为3的等腰三角形,它的两边长是方程x2﹣4x+k=0的两根,则k= .
59.(2023秋 莲都区期末)根据数量关系“x的5倍大于1”,列不等式为 .
60.(2023秋 滨江区期末)如图,把两根钢条的中点连在一起,可以做成一个测量工件内槽宽的工具(卡钳)在图中,若测量得A'B'=10cm,则工件内槽宽AB为 cm.
参考答案与试题解析
一.填空题(共60小题)
1.【答案】25.
【解答】解:如图,过点D作DE⊥AC于点E,作DG⊥BF于点G,
∵点D是∠ACF平分线上的一点,
∴DE=DG,∠DEA=∠DGB,
又∵∠DAC+∠ADB=∠DBC+∠ACB,∠ADB=∠ACB,
∴∠DAC=∠DBC,
∴△ADE≌△BDG(AAS),
∴DA=DB,
又∵∠ABC=90°,∠BAC=40°,
∴∠ADB=∠ACB=90°﹣40°=50°,
∴,
∴∠DAC=∠DAB﹣∠CAB=65°﹣40°=25°,
故答案为:25.
2.【答案】13.
【解答】解:∵a+b=5,
∴(a+b)2=25,
∴a2+2ab+b2=25.
∵ab=6,
∴a2+b2+12=25,
∴a2+b2=13.
故答案为:13.
3.【答案】(3,1).
【解答】解:根据两点关于x轴对称,横坐标不变,纵坐标互为相反数,
∴点M(3,﹣1)关于x轴的对称点的坐标是(3,1),
故答案为:(3,1).
4.【答案】见试题解答内容
【解答】解:∵y﹣1与x+1成正比例,
∴设y﹣1=k(x+1),
∵当x=2时,y=5,
∴5﹣1=k(2+1),
解得,
∴,
即,
故答案为:.
5.【答案】60°
【解答】解:∵∠ABD=15°,∠ABC=90°,
∴∠DBC=∠ABC﹣∠DBC=90°﹣15°=75°,
由折叠可得∠DBE=∠DBC=75°,
∴∠ABE=∠DBE﹣∠ABD=75°﹣15°=60°.
故答案为:60°.
6.【答案】7.
【解答】解:由折叠的性质可知,DC=DE,BE=BC=6,
∵AB=8,
∴AE=AB﹣BE=2,
∴△AED的周长为:AD+AE+DE=AC+AE=7,
故答案为:7.
7.【答案】三角形具有稳定性.
【解答】解:人字梯中间一般会设计一“拉杆”,是为了形成三角形,利用三角形具有稳定性来增加其稳定性,
故答案为:三角形具有稳定性.
8.【答案】见试题解答内容
【解答】解:∵正十边形的每个外角的度数为360°÷10=36°,
∴正十边形的每个内角度数为180°﹣36°=144°.
故答案为:144.
9.【答案】7.
【解答】解:根据题意,得P1D=PD=5.5,P2E=PE=5,ED=EP2+P2D=,6.5,
故P2D=1.5,
故P1P=P1D+P2D=7,
故答案为:7.
10.【答案】见试题解答内容
【解答】解:①5是腰长时,三角形的三边分别为5、5,2,
能组成三角形,
周长=5+5+2=12,
②5是底边时,三角形的三边分别为2、2、5,
不能组成三角形,
故答案为:12.
11.【答案】见试题解答内容
【解答】解:∵∠A+∠B+∠C=180°,∠A=∠B+∠C,
∴2∠A=180°.
∴∠A=90°.
故答案为:直角.
12.【答案】x1=2023或x2=1.
【解答】解:x2﹣2024x+2023=0,
(x﹣2023)(x﹣1)=0,
可得x﹣2023=0或x﹣1=0,
解得x1=2023或x2=1,
故答案为:x1=2023或x2=1.
13.【答案】.
【解答】解:如图,延长AD,BC交于点E,
∵∠ABC=2∠BAD=90°,
∴∠BAE=45°,
∴∠AEB=45°,
∴AB=BE=2,
根据勾股定理可得,
∵,
∴,
过点E作EG⊥AE的垂线段,且使EG=AB,
∵∠ABC=∠GED,AB=EG,
∴△ABC≌△GED(SAS),
∴AC=GD,
∴AC+BD=GD+BD,
AC+BD取最小值时,GD+BD取最小值,即B,D,G三点共线时,取得最小值,
以点B为原点,BA为y轴,BF为y轴,建立平面直角坐标系,过点D,G作x轴的垂线段,交x轴于点H,F,
∴A(0,2),E(2,0),
设直线AE的解析式为y=k1x+b1,
把A(0,2),E(2,0)代入可得,
解得,
∴直线AE的解析式为y=﹣x+2,
∵∠AEB=45°,∠AEG=90°,
∴∠GEF=45°,
设GF=x,则EF=x,
根据勾股定理可得EF2+GF2=EG2,可得x2+x2=22,
解得,
∴,
设BG的解析式为y=k2x,
把代入可得,
解得,
∴BG的解析式为,
联立方程组,
解得,
∴,
∴,
根据勾股定理可得,
∴,
故答案为:.
14.【答案】0<x<1.
【解答】解:把(1,﹣1)代入直线y1=ax+2与y2=bx﹣2,
可得﹣1=a+2,﹣1=b﹣2,
解得a=﹣3,b=1,
∴直线解析式为y1=﹣3x1+2与y2=x2﹣2,
对两边同时平方可得(﹣3x+2)2<(x﹣2)2,
整理后得到8x2﹣8x<0,
即8x(x﹣1)<0,
∴①或②;
解①可得无解;
解②可得0<x<1,
故答案为:0<x<1.
15.【答案】9.7.
【解答】解:当N=13时,
故答案为:9.7.
16.【答案】见试题解答内容
【解答】解:设∠A=x,则∠B=3x,∠C=4x,
∵∠A+∠B+∠C=180°,
∴x+3x+4x=180°,
∴x=22.5°,
∴∠A=22.5°,∠B=67.5°,∠C=90°,
故答案为:直角.
17.【答案】见试题解答内容
【解答】解:依题意,建立平面直角坐标如图所示,
∴“马”所在位置的坐标为(﹣2,﹣2),
故答案为:(﹣2,﹣2).
18.【答案】65.
【解答】解:∵等腰三角形的顶角等于50°,两个底角相等,
∴底角的度数=×(180°﹣50°)=65°.
故答案为:65.
19.【答案】∠A=∠D,理由见解析.
【解答】解:添加的一个条件是∠A=∠D.
理由是:在△ABC和△DEF中,
,
∴△ABC≌△DEF(SAS).
故答案为:∠A=∠D.
20.【答案】10.
【解答】解:∵点A(2,﹣m+1)与点B(n+1,0)关于y轴对称,
∴n+1=﹣2,﹣m+1=0,
解得:m=1,n=﹣3
∴m2+n2=1+9=10,
故答案为:10.
21.【答案】见试题解答内容
【解答】解:①当这个角是顶角时,底角=(180°﹣100°)÷2=40°;
②当这个角是底角时,另一个底角为100°,因为100°+100°=200°,不符合三角形内角和定理,所以舍去.
故答案为:40°.
22.【答案】1;5≤k≤7或﹣5≤k≤﹣3.
【解答】解:(1)当k=﹣1时,l1:y=﹣x+1,l2:y=x+3,
如图所示,设l1、l2交于点B,l2与y轴交于点A,l1与y轴交于点C,则C(0,1),
∴2=x+3,解得:x=﹣1,则B(﹣1,2),
当x=0时,y=3,
∴A(0,3),
∴AC=2,
∴.
故答案为:1;
(2)∵l1:y=kx+2+k=k(x+1)+2,l2:y=x+3,
∴l1过定点(﹣1,2),则点B(﹣1,2)到y轴的距离为1,
设l1与y轴交于点D,则D(0,2+k),则AD=|2+k﹣3|,
∴,
当S=2时,,
解得:k=5或k=﹣3,
当S=3时,,
解得:k=﹣5或k=7,
∵2≤S≤3,
∴5≤k≤7或﹣5≤k≤﹣3,
故答案为:5≤k≤7或﹣5≤k≤﹣3.
23.【答案】见试题解答内容
【解答】解:∵△ABC的等边三角形,
∴∠ACB=60°,
∴∠ACP+∠PCB=60°,
∵∠ACP=∠PBC,
∴∠PCB+∠PBC=60°,
∴∠BPC=180°﹣60°=120°.
故答案为120.
24.【答案】.
【解答】解:如图,连接BH,过点H作BC的平行线交AB于点I,过点B作BJ⊥HI交HI延长线于点J,延长CE,DA交于点K,过点C作CL⊥AD于点L,
由翻折可知:,
∵点H是EC的中点,HI∥BC,ABCD为菱形,
∴,
∴∠JBI=30°,
设IJ=x,
∴,
在Rt△BHJ中,HJ=IJ+HI=x+6,
由勾股定理得:HJ2+BJ2=BH2,
∴,
整理得x2+3x﹣10=0,
解得x1=2,x2=﹣5(舍去负值),
∴IJ=2,
∴BI=4,
∴EI=BI=4,
∴AE=AB﹣EI﹣BI=4,
∴AE=EI,
∵HI∥BC∥AD,
∴∠AKE=∠IHE,
∵∠AEK=∠HEI,
∴△AEK≌△IEH(AAS),
∴AK=IH=6,
由翻折可知:∠BCE=∠FCE,
∵BC∥AD,
∴∠CKG=∠BCE,
∴∠CKG=∠GCE,
∴GK=GC,
设GK=GC=y,
∴AG=GK﹣AK=y﹣6,
∵CL⊥AD,∠D=60°,CD=12,
∴,
∴,
∴AL=AD﹣DL=12﹣6=6,
∴GL=AL﹣AG=6﹣(y﹣6)=12﹣y,
在Rt△GLC中,由勾股定理得:GL2+CL2=GC2,
∴,
∴,
∴,
∴.
故答案为:.
25.【答案】>.
【解答】解:∵a为常数,且a≠0,
∴a2>0,
∴a2+1>0,
∴y随x的增大而增大.
又∵一次函数y=(a2+1)x﹣3(a为常数,且a≠0)的图象过P(x1,y1),Q(x2,y2)点,且x1>x2,
∴y1>y2.
故答案为:>.
26.【答案】(0,﹣2).
【解答】解:将x=0代入y=2x﹣2,可得y=﹣2,
故一次函数y=2x﹣2的图象与y轴的交点坐标是(0,﹣2).
故答案为:(0,﹣2).
27.【答案】2.
【解答】解:在正方形ABCD中,AC和BD为对角线,
∴∠AOB=∠BOC=90°,∠OBC=∠OCD=45°,OB=OC,
∵∠AOE=150°,
∴∠BOE=60°;
∵OE⊥OF,
∴∠EOF=∠BOC=90°,
∴∠BOE=∠COF=60°,
∴△BOE≌△COF(ASA),
∴OE=OF,
∴△OEF是等腰直角三角形,
∴OF=EF=2,
过点F作FG⊥OD于G,如图,
∵∠AOE=150°,
∴∠BOE=60°,
∴∠DOF=30°,
∴GF=OF=,
∴∠OGF=∠DGF=90°,
∵∠ODC=45°,
∴△DGF是等腰直角三角形,
∴DF=GF=2,
故答案为:2.
28.【答案】4.
【解答】解:在平行四边形ABCD中,
AB=CD=4,AD∥BC,
∴∠DAE=∠AEB,
∵AE平分∠BAD,
∴∠BAE=∠DAE,
∴∠BAE=∠AEB,
∴AB=BE=4,
故答案为:4.
29.【答案】见试题解答内容
【解答】解:∵方程x2+(2k+1)x+k2=0的两个实数根的平方和是7,
∴x1+x2=﹣2k﹣1,x1x2=k2,(2k+1)2﹣4k2≥0,即k≥﹣,
∵x12+x22=7,
∴(x1+x2)2﹣2x1x2=(2k+1)2﹣2k2=7,
整理得:2k2+4k﹣6=0,
分解因式得:(2k+6)(k﹣1)=0,
解得:k=﹣3(不符合题意,舍去)或k=1,
故答案为:1
30.【答案】x<﹣.
【解答】解:由题意可知﹣2x+1>2,
解得x<﹣,
故答案为:x<﹣.
31.【答案】见试题解答内容
【解答】解:∵点A(﹣5m,2m﹣1)向上平移3个单位,
∴点A1(﹣5m,2m﹣1+3)向上平移3个单位,
∵点A1(﹣5m,2m﹣1+3)在x轴上,
∴2m﹣1+3=0,解得:m=﹣1,
故答案为:﹣1.
32.【答案】见试题解答内容
【解答】解:∵∠ACB=90°,AC=3,BC=4,由勾股定理得:AB==5,
∵CD是△ABC中线,
∴CD=AB=×5=2.5,
故答案为:2.5.
33.【答案】3x﹣4≥2.
【解答】解:由题意得:3x﹣4≥2.
故答案为:3x﹣4≥2.
34.【答案】m≤2.
【解答】解:不等式组整理得:,
∵不等式组的解集为x>2,
∴m的范围是m≤2.
故答案为:m≤2.
35.【答案】见试题解答内容
【解答】解:∵一次函数y=(2m﹣6)x+5中,y随x的增大而减小,
∴2m﹣6<0,
解得,m<3;
故答案为:m<3.
36.【答案】3.
【解答】解:∵△ABC≌△DEF,
∴EF=BC=7cm,
∴CF=EF﹣CE=3cm;
故答案为:3.
37.【答案】(1);(2).
【解答】解:(1)设AF=EG=DH=BK=BC=a,FK=GF=HG=HK=b,
∵若Rt△ABF的面积为5,小正方形FGHK的面积为9,
∴a(a+b)=5,b2=9,
∴a2+ab=10,
∵AB2=a2+(a+b)2,
∴AB==,
故答案为:;
(2)∵SAEHN=S△AEG+SAGHN=+b(a+b)=,=,
∴=k(),
∴()(b+a)=0,
∴b=,
∴==,
故答案为:.
38.【答案】3.
【解答】解:设BE=x,则CE=4x,BE:CE=1:4,
∴AD=BC=BE+CE=5x,
∵AE平分∠BED,
∴∠BEA=∠DEA,
∵BC∥AD,
∴∠DAE=∠DEA,
∴AD=DE=5x,
在Rt△CDE中,CD==3x,
∴AB=CD=3x
∴k==3
故答案为:3.
39.【答案】见试题解答内容
【解答】解:∵点P的坐标为(﹣2023,2024),
∴点P在第二象限.
故答案为:二.
40.【答案】1:2.
【解答】解:∵AD是BC边上的中线,
∴S△ABD=S△ACD,
∵DE⊥AC,DF⊥AB,AB=2AC,
∴,
即2AC DE=AC DF,
∴2DE=DF,
∴DE:DF=1:2,
即DE与DF的长度之比是1:2,
故答案为:1:2.
41.【答案】14.
【解答】解:不等式的解集是:x≤,
∵不等式的正整数解恰是1,2,3,4,
∴4≤<5,
∴a的取值范围是14≤a<17.
∴整数a的最小值是14.
故答案为:14.
42.【答案】.
【解答】解:对于一次函数y=4x﹣6来说,
当y=0时,4x﹣6=0,
解得,
∴一次函数y=4x﹣6与x轴的交点坐标为,
故答案为:.
43.【答案】①②④.
【解答】解:根据旋转的性质知∠CAD=∠BAF,AD=AF,
∵∠BAC=90°,∠DAE=45°,
∴∠CAD+∠BAE=∠BAF+∠BAE=45°.
∴∠EAF=45°,
在△AED和△AEF中,
,
∴△AED≌△AEF(SAS);
故①正确;
在Rt△ABC中,AB=AC,
∴∠ABC=∠C=45°,∠BAC=90°,
由△AED≌△AEF可知DE=EF,BF=CD,∠ABF=∠C=45°,∠BAF=∠CAD,
∴∠FAD=∠BAF+∠BAD=∠CAD+∠BAD=∠BAC=90°,
故②正确;
由旋转可知CD=BF,
∴BE+DC=BE+BF>EF.
∵DE=EF,
∴BE+CD>DE.
故③错误;
∵∠EBF=∠ABF+∠ABC=90°,
∴在Rt△BEF中,BE2+BF2=EF2,
∵△AED≌△AEF(SAS);
∴DE=EF,
∴BE2+CD2=DE2,
故④正确,
综上,正确的为①②④.
故答案为:①②④.
44.【答案】;6.
【解答】解:(1)根据题意得:联立得,,
解得;;
∴;
故答案为:;
(2)∵将两个函数图象向右平移m个单位,
∴,
∴,,
当O、C、D三点共线时,|OC﹣OD|最小,
∴设O、C、D所在直线为正比例函数y=kx,
将点代入得:
,
解得:m=6,
故答案为:6.
45.【答案】﹣9.
【解答】解:∵点A(2,m+3),B(n,﹣4)关于y轴对称,
∴n=﹣2,m+3=﹣4,
解得m=﹣7,n=﹣2,
∴m+n=﹣7﹣2=﹣9.
故答案为:﹣9.
46.【答案】80.
【解答】解:∵AD⊥BC,
∴∠ADB=90°.
在△ABD中,∠B=30°,∠ADB=90°,
∴∠BAD=180°﹣∠B﹣∠ADB=180°﹣30°﹣90°=60°,
∴∠BAE=∠BAD﹣∠1=60°﹣25°=35°.
∵AE平分∠BAC,
∴∠BAC=2∠BAE=2×35°=70°.
在△ABC中,∠B=30°,∠BAC=70°,
∴∠C=180°﹣∠B﹣∠BAC=180°﹣30°﹣70°=80°.
故答案为:80.
47.【答案】如果两个角是对顶角,那么它们相等.
【解答】解:题设为:对顶角,结论为:相等,
故写成“如果…那么…”的形式是:如果两个角是对顶角,那么它们相等;
故答案为:如果两个角是对顶角,那么它们相等.
48.【答案】y3.
【解答】解:∵k=﹣9<0,
∴y随x增大而减小,
∵A(﹣1,y1),B(﹣0.5,y2),C(1.7,y3),﹣1<﹣0.5<1.7,
∴y1>y2>y3,
故答案为:y3.
49.【答案】﹣1.
【解答】解:∵点E的坐标为(﹣2,﹣n),其关于y轴对称的点F的坐标(2,﹣m+1),
∴﹣n=﹣m+1,
∴n﹣m=﹣1,
∴(n﹣m)2023=(﹣1)2023=﹣1.
故答案为:﹣1.
50.【答案】10.
【解答】解:∵在两个全等的三角形中,已知一个三角形的三个内角为30°,α,β(α>β),另一个三角形有一个角为70°,
∴α=70°或β=70°,
当α=70°,β=80°,
∵α>β,
∴这种情况不存在,
当β=70°,α=80°,
∴α﹣β=80°﹣70°=10°,
故答案为:10.
51.【答案】见试题解答内容
【解答】解:过O作OE⊥AB于点E,
∵BO平分∠ABD,OD⊥BC于点D,
∴OD=OE=5,
∴△AOB的面积=,
故答案为:15.
52.【答案】50.
【解答】解:把(12,600)代入y=k1x得:k1==50;
把(20,600),(28,1400)代入y=k2x+b得:
,
解得,
∴k2﹣k1=100﹣50=50.
故答案为:50.
53.【答案】.
【解答】解:∵(x1﹣x2)(y1﹣y2)<0,
∵(x1﹣x2)>0,(y1﹣y2)<0,或(x1﹣x2)<0,(y1﹣y2)>0.
∴x1>x2,y1<y2,或x1<x2,y1>y2.
即y随x的增大而减小或y随x的减小而增大.
∴2﹣5a<0.
∴.
故答案为:.
54.【答案】见试题解答内容
【解答】解:如图所示:
由平移的性质可知:∠2=∠3.
又∵∠1=∠2,
∴∠3=∠1.
∴EF∥l(内错角相等,两直线平行).
故答案为:内错角相等,两直线平行.
55.【答案】x=1.
【解答】解:原方程去分母得:6x=x+5,
解得:x=1,
检验:将x=1代入2x(x+5)得2×1×6=12≠0,
故原方程的解为x=1,
故答案为:x=1.
56.【答案】x≠2.
【解答】解:要使分式有意义,
则x﹣2≠0,
解得,x≠2,
故答案为:x≠2.
57.【答案】见试题解答内容
【解答】解:作CH⊥AB于H,连接OH,如图,
∵AC=BC=25,AB=14,
∴AH=BH=AB=7,
在Rt△BCH中,CH===24,
∵OC≥CH﹣OH(当点C、O、H共线时取等号),
∴OC的最小值为24﹣7=17.
故答案为:17.
58.【答案】见试题解答内容
【解答】解:当该等腰三角形的腰长是3时,根据韦达定理知
3+x2=4,
∴x2=1,
∴x1 x2=3=k,即k=3;
当该等腰三角形的腰长不是3时,Δ=16﹣4k=0,
解得,k=4;
综上所述,k=3或k=4.
故答案为:3或4.
59.【答案】5x>1.
【解答】解:“x的5倍大于1”,可表示为5x>1,
故答案为:5x>1.
60.【答案】10.
【解答】解:连接A′B′,如图,
∵点O分别是AA′、BB′的中点,
∴OA=OA′,OB=OB′,
在△AOB和△A′OB′中,
,
∴△AOB≌△A′OB′(SAS).
∴A′B′=AB,
∵A'B'=10cm,
∴AB=10cm,
故答案为:10.
声明:
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
专题02 填空题
一.填空题(共60小题)
1.(2023秋 台州期末)如图,在△ABC中,∠ABC=90°,∠BAC=40°,点D是△ABC外角∠ACF平分线上的一点,连接AD、BD,若∠ADB=∠ACB,则∠DAC= 度.
2.(2023秋 温岭市期末)已知a+b=5,ab=6.则a2+b2= .
3.(2023秋 义乌市期末)点M(3,﹣1)关于x轴的对称点的坐标为 .
4.(2023秋 瓯海区校级期末)若y﹣1与x+1成正比例,且当x=2时,y=5,则y与x之间的函数表达式为 .
5.(2023秋 柯桥区期末)如图,在Rt△ABC中,∠ABC=90°,点D为AC边上一动点,将△CBD沿着直线BD对折得到△EBD.若∠ABD=15°,则∠ABE的度数为 .
6.(2023秋 瓯海区校级期末)如图的三角形纸片中,AB=8,BC=6,AC=5,沿过点B的直线折叠这个三角形,使点C落在AB边上的点E处,折痕为BD,则△ADE的周长为 .
7.(2023秋 海曙区期末)如图所示,人字梯中间一般会设计一“拉杆”,这样做的依据是 .
8.(2023秋 台州期末)正十边形的每个内角度数为 °.
9.(2023秋 瓯海区校级期末)如图,点P是∠ACB外一点,点D,E分别是CB,CA上的点,点P关于BC的对称点P1落在线段ED的延长线上,点P关于AC的对称点P2恰巧落在ED上.若PE=5,PD=5.5,ED=6.5,则线段P1P2的长为 .
10.(2023秋 海曙区校级期末)若等腰三角形有两条边长分别为2和5,则这个等腰三角形的周长为 .
11.(2023秋 海曙区校级期末)已知,在△ABC中,∠A=∠B+∠C,则△ABC是 三角形.
12.(2023秋 鄞州区期末)方程x2﹣2024x+2023=0的解为 .
13.(2023秋 鄞州区期末)如图,D是△ABC外一点,∠ABC=2∠BAD=90°,BC<AB,AB=2,若,则AC+BD取最小值时,AD﹣BC= .
14.(2023秋 鄞州区期末)在平面直角坐标系中,直线y1=ax+2与y2=bx﹣2交于点(1,﹣1),则不等式的解集为 .
15.(2023秋 舟山期末)根据科学研究表明,10至50岁的人每天所需睡眠时间H(时)可用公式(N是人的年龄).请你用这个公式计算,13岁的小明每天需要睡眠时间 (时).
16.(2023秋 镇海区校级期末)在△ABC中,已知∠A:∠B:∠C=1:3:4,那么△ABC是 三角形(填“锐角”、“直角”或“钝角”).
17.(2023秋 衢江区期末)象棋在中国有着三千多年的历史,老少皆宜.其中棋盘、棋子都蕴含着中国文化,如图,已知“炮”所在位置的坐标为(﹣2,1),“士”所在位置的坐标为(0,﹣2),“相”所在位置的坐标为(3,﹣2),则“马”所在位置的坐标为 .
18.(2023秋 吴兴区期末)已知等腰三角形的顶角等于50°,则底角的度数为 度.
19.(2023秋 瓯海区校级期末)如图所示,A,E,B,D在同一直线上,AB=DE,AC=DF,要使△ABC≌△DEF,需添加的一个条件是 ,并说明理由.
20.(2023秋 莲都区期末)在平面直角坐标系中,点A(2,﹣m+1)与点B(n+1,0)关于y轴对称,则代数式m2+n2的值为 .
21.(2023秋 宁波期末)等腰三角形的一个内角为100°,则它的一个底角的度数为 .
22.(2023秋 莲都区期末)已知直线l1:y=kx+2+k(k≠0)和直线l2:y=x+3.若直线l1、l2与y轴所围成的三角形面积记作S.
(1)当k=﹣1时,S的值是 ;
(2)当2≤S≤3时,k的取值范围是 .
23.(2023秋 瓯海区校级期末)如图,点P是等边△ABC内一点,∠ACP=∠PBC,∠BPC= °.
24.(2023秋 江北区期末)如图,菱形ABCD中,AB=12,∠B=60°,点E是AB上一点,将菱形沿着EC折叠,使点B落在点F处,CF与AD交于点G,点H是EC的中点,,则FG的长为 .
25.(2023秋 江北区期末)已知一次函数y=(a2+1)x﹣3(a为常数,且a≠0)的图象过P(x1,y1),Q(x2,y2)点,若x1>x2,则y1 y2.(用>或<填空)
26.(2023秋 江北区期末)一次函数y=2x﹣2的图象与y轴交点坐标为 .
27.(2023秋 江北区期末)如图,在正方形ABCD中,O为对角线AC,BD的交点,E,F分别为边BC,CD上一点,连接OE,OF,EF,OE⊥OF.若∠AOE=150°,EF=4,则DF的长为 .
28.(2023秋 江北区期末)如图,在平行四边形ABCD中,AE平分∠BAD,E为BC上一点,若CD=4,则BE= .
29.(2023秋 江北区期末)已知关于x的方程x2+(2k+1)x+k2=0的两个实数根的平方和是7,则k= .
30.(2023秋 金东区期末)如图,在数轴上点M、N分别表示数2,﹣2x+1,则x的取值范围是 .
31.(2023秋 武义县期末)若点A(﹣5m,2m﹣1)向上平移3个单位后得到的点在x轴上,则m的值为 .
32.(2023秋 北仑区期末)若直角三角形的两条直角边的长分别是3和4,则斜边上的中线长为 .
33.(2023秋 瓯海区校级期末)“x的3倍与4的差不小于2”用不等式可表示为 .
34.(2023秋 镇海区校级期末)不等式组的解集是x>2,则m的取值范围是 .
35.(2023秋 余姚市期末)一次函数y=(2m﹣6)x+5中,y随x的增大而减小,则m的取值范围是 .
36.(2023秋 衢州期末)如图,若△ABC≌△DEF,B、E、C、F在同一直线上,BC=7cm,CE=4cm,则CF的长是 cm.
37.(2023秋 婺城区期末)图1是由5个全等的直角三角形与一个小正方形组成,延长DK交AB、AC分别于点M、N,延长EH交BD于点P(如图2).
(1)若Rt△ABF的面积为5,小正方形FGHK的面积为9,则AB= ;
(2)如图2,若,则= (用含k的代数式表示).
38.(2023秋 婺城区期末)如图,将长方形ABCD放置于平面直角坐标系中,点C在第一象限,点A与坐标原点重合,过点A的直线y=kx交BC于点E,连结DE,已知BE:CE=1:4,AE平分∠BED,则k的值为 .
39.(2023秋 柯桥区期末)在平面直角坐标系中,点P(﹣2023,2024)在第 象限.
40.(2023秋 浦江县期末)如图,在△ABC中,AD是BC边上的中线,DE⊥AC,DF⊥AB,E,F分别是垂足.已知AB=2AC,则DE与DF的长度之比是 .
41.(2023秋 义乌市期末)若关于x的不等式3x+2≤a的正整数解是1,2,3,4,则整数a的最小值是 .
42.(2023秋 浦江县期末)一次函数y=4x﹣6与x轴的交点坐标为 .
43.(2023秋 浦江县期末)在Rt△ABC中,AB=AC,D,E是斜边BC上的两点,且∠DAE=45°.现将△ADC绕点A旋转90°后得到△AFB,连EF,有下面结论:
①△AED≌△AEF;
②∠FAD=90°;
③BE+CD=DE;
④BE2+CD2=DE2.
其中正确的结论是 .
44.(2023秋 浦江县期末)已知直线与函数的图象相交于A,B两点(点A在点B左侧).
(1)点B的坐标是 .
(2)若坐标原点为点O,将两个函数图象向右平移m个单位,点A,B平移后分别对应点C,D,连接OC,OD,当|OC﹣OD|最大时,m的值为 .
45.(2023秋 鄞州区期末)已知点A(2,m+3),B(n,﹣4)关于y轴对称,则m+n= .
46.(2023秋 金东区期末)如图,在△ABC中,AB>AC,AD、AE分别是△ABC的高线和角平分线,若AD与AE构成的角为∠1=25°,∠B=30°,则∠C= 度.
47.(2023秋 滨江区期末)将“对顶角相等”改写为“如果…那么…”的形式,可写为 .
48.(2023秋 武义县期末)已知A(﹣1,y1),B(﹣0.5,y2),C(1.7,y3),是直线y=﹣9x+b(b为常数)上的三个点,则y1,y2,y3中最小的是 .
49.(2023秋 婺城区期末)剪纸艺术是最古老的中国民间艺术之一,很多剪纸作品体现了数学中的对称美.如图,蝴蝶剪纸是一幅轴对称图形,将其放在平面直角坐标系中,点E的坐标为(﹣2,﹣n),其关于y轴对称的点F的坐标(2,﹣m+1),则(n﹣m)2023= .
50.(2023秋 婺城区期末)在两个全等的三角形中,已知一个三角形的三个内角为30°,α,β(α>β),另一个三角形有一个角为70°,则α﹣β= °.
51.(2023秋 玉环市期末)如图,点O是△ABC内一点,BO平分∠ABC,OD⊥BC于点D,连接OA.若OD=3,AB=10,则△AOB的面积是 .
52.(2023秋 西湖区期末)如图,图中的折线OABC反映了圆圆从家到学校所走的路程S(m)与时间t(min)的函数关系,其中,OA所在直线的表达式为y=k1x(k1≠0),BC所在直线的表达式为y=k2x+b(k2≠0),则k2﹣k1= .
53.(2023秋 舟山期末)已知关于x的一次函数y=(2﹣5a)x+3的图象上有任意两个点(x1,y1),(x2,y2)若(x1﹣x2)(y1﹣y2)<0,则a的取值范围是 .
54.(2023秋 宁波期末)阅读下面材料:在数学课上,老师提出如下问题:
作图:过直线外一点作已知直线的平行线.
已知:直线l及其外一点A(如图1).
求作:l的平行线,使它经过点A.
小凡利用两块形状相同的三角尺进行如下操作:
如图2所示:
(1)用第一块三角尺的一条边贴住直线l,第二块三角尺的一条边紧靠第一块三角尺;
(2)将第二块三角尺沿第一块三角尺移动,使其另一边经过点A,沿这边作出直线AB,所以,直线AB即为所求.
老师说:“小凡的作法正确.”
请回答:小凡的作图依据是 .
55.(2023秋 台州期末)分式方程的解为 .
56.(2023秋 台州期末)分式有意义的条件是 .
57.(2023秋 海曙区校级期末)如图,∠MON=90°,已知△ABC中,AC=BC=25,AB=14,△ABC的顶点A、B分别在边OM、ON上,当点B在边ON上运动时,A随之在OM上运动,△ABC的形状始终保持不变,在运动的过程中,点C到点O的最小距离为 .
58.(2023秋 海曙区校级期末)有一边长为3的等腰三角形,它的两边长是方程x2﹣4x+k=0的两根,则k= .
59.(2023秋 莲都区期末)根据数量关系“x的5倍大于1”,列不等式为 .
60.(2023秋 滨江区期末)如图,把两根钢条的中点连在一起,可以做成一个测量工件内槽宽的工具(卡钳)在图中,若测量得A'B'=10cm,则工件内槽宽AB为 cm.
参考答案与试题解析
一.填空题(共60小题)
1.【答案】25.
【解答】解:如图,过点D作DE⊥AC于点E,作DG⊥BF于点G,
∵点D是∠ACF平分线上的一点,
∴DE=DG,∠DEA=∠DGB,
又∵∠DAC+∠ADB=∠DBC+∠ACB,∠ADB=∠ACB,
∴∠DAC=∠DBC,
∴△ADE≌△BDG(AAS),
∴DA=DB,
又∵∠ABC=90°,∠BAC=40°,
∴∠ADB=∠ACB=90°﹣40°=50°,
∴,
∴∠DAC=∠DAB﹣∠CAB=65°﹣40°=25°,
故答案为:25.
2.【答案】13.
【解答】解:∵a+b=5,
∴(a+b)2=25,
∴a2+2ab+b2=25.
∵ab=6,
∴a2+b2+12=25,
∴a2+b2=13.
故答案为:13.
3.【答案】(3,1).
【解答】解:根据两点关于x轴对称,横坐标不变,纵坐标互为相反数,
∴点M(3,﹣1)关于x轴的对称点的坐标是(3,1),
故答案为:(3,1).
4.【答案】见试题解答内容
【解答】解:∵y﹣1与x+1成正比例,
∴设y﹣1=k(x+1),
∵当x=2时,y=5,
∴5﹣1=k(2+1),
解得,
∴,
即,
故答案为:.
5.【答案】60°
【解答】解:∵∠ABD=15°,∠ABC=90°,
∴∠DBC=∠ABC﹣∠DBC=90°﹣15°=75°,
由折叠可得∠DBE=∠DBC=75°,
∴∠ABE=∠DBE﹣∠ABD=75°﹣15°=60°.
故答案为:60°.
6.【答案】7.
【解答】解:由折叠的性质可知,DC=DE,BE=BC=6,
∵AB=8,
∴AE=AB﹣BE=2,
∴△AED的周长为:AD+AE+DE=AC+AE=7,
故答案为:7.
7.【答案】三角形具有稳定性.
【解答】解:人字梯中间一般会设计一“拉杆”,是为了形成三角形,利用三角形具有稳定性来增加其稳定性,
故答案为:三角形具有稳定性.
8.【答案】见试题解答内容
【解答】解:∵正十边形的每个外角的度数为360°÷10=36°,
∴正十边形的每个内角度数为180°﹣36°=144°.
故答案为:144.
9.【答案】7.
【解答】解:根据题意,得P1D=PD=5.5,P2E=PE=5,ED=EP2+P2D=,6.5,
故P2D=1.5,
故P1P=P1D+P2D=7,
故答案为:7.
10.【答案】见试题解答内容
【解答】解:①5是腰长时,三角形的三边分别为5、5,2,
能组成三角形,
周长=5+5+2=12,
②5是底边时,三角形的三边分别为2、2、5,
不能组成三角形,
故答案为:12.
11.【答案】见试题解答内容
【解答】解:∵∠A+∠B+∠C=180°,∠A=∠B+∠C,
∴2∠A=180°.
∴∠A=90°.
故答案为:直角.
12.【答案】x1=2023或x2=1.
【解答】解:x2﹣2024x+2023=0,
(x﹣2023)(x﹣1)=0,
可得x﹣2023=0或x﹣1=0,
解得x1=2023或x2=1,
故答案为:x1=2023或x2=1.
13.【答案】.
【解答】解:如图,延长AD,BC交于点E,
∵∠ABC=2∠BAD=90°,
∴∠BAE=45°,
∴∠AEB=45°,
∴AB=BE=2,
根据勾股定理可得,
∵,
∴,
过点E作EG⊥AE的垂线段,且使EG=AB,
∵∠ABC=∠GED,AB=EG,
∴△ABC≌△GED(SAS),
∴AC=GD,
∴AC+BD=GD+BD,
AC+BD取最小值时,GD+BD取最小值,即B,D,G三点共线时,取得最小值,
以点B为原点,BA为y轴,BF为y轴,建立平面直角坐标系,过点D,G作x轴的垂线段,交x轴于点H,F,
∴A(0,2),E(2,0),
设直线AE的解析式为y=k1x+b1,
把A(0,2),E(2,0)代入可得,
解得,
∴直线AE的解析式为y=﹣x+2,
∵∠AEB=45°,∠AEG=90°,
∴∠GEF=45°,
设GF=x,则EF=x,
根据勾股定理可得EF2+GF2=EG2,可得x2+x2=22,
解得,
∴,
设BG的解析式为y=k2x,
把代入可得,
解得,
∴BG的解析式为,
联立方程组,
解得,
∴,
∴,
根据勾股定理可得,
∴,
故答案为:.
14.【答案】0<x<1.
【解答】解:把(1,﹣1)代入直线y1=ax+2与y2=bx﹣2,
可得﹣1=a+2,﹣1=b﹣2,
解得a=﹣3,b=1,
∴直线解析式为y1=﹣3x1+2与y2=x2﹣2,
对两边同时平方可得(﹣3x+2)2<(x﹣2)2,
整理后得到8x2﹣8x<0,
即8x(x﹣1)<0,
∴①或②;
解①可得无解;
解②可得0<x<1,
故答案为:0<x<1.
15.【答案】9.7.
【解答】解:当N=13时,
故答案为:9.7.
16.【答案】见试题解答内容
【解答】解:设∠A=x,则∠B=3x,∠C=4x,
∵∠A+∠B+∠C=180°,
∴x+3x+4x=180°,
∴x=22.5°,
∴∠A=22.5°,∠B=67.5°,∠C=90°,
故答案为:直角.
17.【答案】见试题解答内容
【解答】解:依题意,建立平面直角坐标如图所示,
∴“马”所在位置的坐标为(﹣2,﹣2),
故答案为:(﹣2,﹣2).
18.【答案】65.
【解答】解:∵等腰三角形的顶角等于50°,两个底角相等,
∴底角的度数=×(180°﹣50°)=65°.
故答案为:65.
19.【答案】∠A=∠D,理由见解析.
【解答】解:添加的一个条件是∠A=∠D.
理由是:在△ABC和△DEF中,
,
∴△ABC≌△DEF(SAS).
故答案为:∠A=∠D.
20.【答案】10.
【解答】解:∵点A(2,﹣m+1)与点B(n+1,0)关于y轴对称,
∴n+1=﹣2,﹣m+1=0,
解得:m=1,n=﹣3
∴m2+n2=1+9=10,
故答案为:10.
21.【答案】见试题解答内容
【解答】解:①当这个角是顶角时,底角=(180°﹣100°)÷2=40°;
②当这个角是底角时,另一个底角为100°,因为100°+100°=200°,不符合三角形内角和定理,所以舍去.
故答案为:40°.
22.【答案】1;5≤k≤7或﹣5≤k≤﹣3.
【解答】解:(1)当k=﹣1时,l1:y=﹣x+1,l2:y=x+3,
如图所示,设l1、l2交于点B,l2与y轴交于点A,l1与y轴交于点C,则C(0,1),
∴2=x+3,解得:x=﹣1,则B(﹣1,2),
当x=0时,y=3,
∴A(0,3),
∴AC=2,
∴.
故答案为:1;
(2)∵l1:y=kx+2+k=k(x+1)+2,l2:y=x+3,
∴l1过定点(﹣1,2),则点B(﹣1,2)到y轴的距离为1,
设l1与y轴交于点D,则D(0,2+k),则AD=|2+k﹣3|,
∴,
当S=2时,,
解得:k=5或k=﹣3,
当S=3时,,
解得:k=﹣5或k=7,
∵2≤S≤3,
∴5≤k≤7或﹣5≤k≤﹣3,
故答案为:5≤k≤7或﹣5≤k≤﹣3.
23.【答案】见试题解答内容
【解答】解:∵△ABC的等边三角形,
∴∠ACB=60°,
∴∠ACP+∠PCB=60°,
∵∠ACP=∠PBC,
∴∠PCB+∠PBC=60°,
∴∠BPC=180°﹣60°=120°.
故答案为120.
24.【答案】.
【解答】解:如图,连接BH,过点H作BC的平行线交AB于点I,过点B作BJ⊥HI交HI延长线于点J,延长CE,DA交于点K,过点C作CL⊥AD于点L,
由翻折可知:,
∵点H是EC的中点,HI∥BC,ABCD为菱形,
∴,
∴∠JBI=30°,
设IJ=x,
∴,
在Rt△BHJ中,HJ=IJ+HI=x+6,
由勾股定理得:HJ2+BJ2=BH2,
∴,
整理得x2+3x﹣10=0,
解得x1=2,x2=﹣5(舍去负值),
∴IJ=2,
∴BI=4,
∴EI=BI=4,
∴AE=AB﹣EI﹣BI=4,
∴AE=EI,
∵HI∥BC∥AD,
∴∠AKE=∠IHE,
∵∠AEK=∠HEI,
∴△AEK≌△IEH(AAS),
∴AK=IH=6,
由翻折可知:∠BCE=∠FCE,
∵BC∥AD,
∴∠CKG=∠BCE,
∴∠CKG=∠GCE,
∴GK=GC,
设GK=GC=y,
∴AG=GK﹣AK=y﹣6,
∵CL⊥AD,∠D=60°,CD=12,
∴,
∴,
∴AL=AD﹣DL=12﹣6=6,
∴GL=AL﹣AG=6﹣(y﹣6)=12﹣y,
在Rt△GLC中,由勾股定理得:GL2+CL2=GC2,
∴,
∴,
∴,
∴.
故答案为:.
25.【答案】>.
【解答】解:∵a为常数,且a≠0,
∴a2>0,
∴a2+1>0,
∴y随x的增大而增大.
又∵一次函数y=(a2+1)x﹣3(a为常数,且a≠0)的图象过P(x1,y1),Q(x2,y2)点,且x1>x2,
∴y1>y2.
故答案为:>.
26.【答案】(0,﹣2).
【解答】解:将x=0代入y=2x﹣2,可得y=﹣2,
故一次函数y=2x﹣2的图象与y轴的交点坐标是(0,﹣2).
故答案为:(0,﹣2).
27.【答案】2.
【解答】解:在正方形ABCD中,AC和BD为对角线,
∴∠AOB=∠BOC=90°,∠OBC=∠OCD=45°,OB=OC,
∵∠AOE=150°,
∴∠BOE=60°;
∵OE⊥OF,
∴∠EOF=∠BOC=90°,
∴∠BOE=∠COF=60°,
∴△BOE≌△COF(ASA),
∴OE=OF,
∴△OEF是等腰直角三角形,
∴OF=EF=2,
过点F作FG⊥OD于G,如图,
∵∠AOE=150°,
∴∠BOE=60°,
∴∠DOF=30°,
∴GF=OF=,
∴∠OGF=∠DGF=90°,
∵∠ODC=45°,
∴△DGF是等腰直角三角形,
∴DF=GF=2,
故答案为:2.
28.【答案】4.
【解答】解:在平行四边形ABCD中,
AB=CD=4,AD∥BC,
∴∠DAE=∠AEB,
∵AE平分∠BAD,
∴∠BAE=∠DAE,
∴∠BAE=∠AEB,
∴AB=BE=4,
故答案为:4.
29.【答案】见试题解答内容
【解答】解:∵方程x2+(2k+1)x+k2=0的两个实数根的平方和是7,
∴x1+x2=﹣2k﹣1,x1x2=k2,(2k+1)2﹣4k2≥0,即k≥﹣,
∵x12+x22=7,
∴(x1+x2)2﹣2x1x2=(2k+1)2﹣2k2=7,
整理得:2k2+4k﹣6=0,
分解因式得:(2k+6)(k﹣1)=0,
解得:k=﹣3(不符合题意,舍去)或k=1,
故答案为:1
30.【答案】x<﹣.
【解答】解:由题意可知﹣2x+1>2,
解得x<﹣,
故答案为:x<﹣.
31.【答案】见试题解答内容
【解答】解:∵点A(﹣5m,2m﹣1)向上平移3个单位,
∴点A1(﹣5m,2m﹣1+3)向上平移3个单位,
∵点A1(﹣5m,2m﹣1+3)在x轴上,
∴2m﹣1+3=0,解得:m=﹣1,
故答案为:﹣1.
32.【答案】见试题解答内容
【解答】解:∵∠ACB=90°,AC=3,BC=4,由勾股定理得:AB==5,
∵CD是△ABC中线,
∴CD=AB=×5=2.5,
故答案为:2.5.
33.【答案】3x﹣4≥2.
【解答】解:由题意得:3x﹣4≥2.
故答案为:3x﹣4≥2.
34.【答案】m≤2.
【解答】解:不等式组整理得:,
∵不等式组的解集为x>2,
∴m的范围是m≤2.
故答案为:m≤2.
35.【答案】见试题解答内容
【解答】解:∵一次函数y=(2m﹣6)x+5中,y随x的增大而减小,
∴2m﹣6<0,
解得,m<3;
故答案为:m<3.
36.【答案】3.
【解答】解:∵△ABC≌△DEF,
∴EF=BC=7cm,
∴CF=EF﹣CE=3cm;
故答案为:3.
37.【答案】(1);(2).
【解答】解:(1)设AF=EG=DH=BK=BC=a,FK=GF=HG=HK=b,
∵若Rt△ABF的面积为5,小正方形FGHK的面积为9,
∴a(a+b)=5,b2=9,
∴a2+ab=10,
∵AB2=a2+(a+b)2,
∴AB==,
故答案为:;
(2)∵SAEHN=S△AEG+SAGHN=+b(a+b)=,=,
∴=k(),
∴()(b+a)=0,
∴b=,
∴==,
故答案为:.
38.【答案】3.
【解答】解:设BE=x,则CE=4x,BE:CE=1:4,
∴AD=BC=BE+CE=5x,
∵AE平分∠BED,
∴∠BEA=∠DEA,
∵BC∥AD,
∴∠DAE=∠DEA,
∴AD=DE=5x,
在Rt△CDE中,CD==3x,
∴AB=CD=3x
∴k==3
故答案为:3.
39.【答案】见试题解答内容
【解答】解:∵点P的坐标为(﹣2023,2024),
∴点P在第二象限.
故答案为:二.
40.【答案】1:2.
【解答】解:∵AD是BC边上的中线,
∴S△ABD=S△ACD,
∵DE⊥AC,DF⊥AB,AB=2AC,
∴,
即2AC DE=AC DF,
∴2DE=DF,
∴DE:DF=1:2,
即DE与DF的长度之比是1:2,
故答案为:1:2.
41.【答案】14.
【解答】解:不等式的解集是:x≤,
∵不等式的正整数解恰是1,2,3,4,
∴4≤<5,
∴a的取值范围是14≤a<17.
∴整数a的最小值是14.
故答案为:14.
42.【答案】.
【解答】解:对于一次函数y=4x﹣6来说,
当y=0时,4x﹣6=0,
解得,
∴一次函数y=4x﹣6与x轴的交点坐标为,
故答案为:.
43.【答案】①②④.
【解答】解:根据旋转的性质知∠CAD=∠BAF,AD=AF,
∵∠BAC=90°,∠DAE=45°,
∴∠CAD+∠BAE=∠BAF+∠BAE=45°.
∴∠EAF=45°,
在△AED和△AEF中,
,
∴△AED≌△AEF(SAS);
故①正确;
在Rt△ABC中,AB=AC,
∴∠ABC=∠C=45°,∠BAC=90°,
由△AED≌△AEF可知DE=EF,BF=CD,∠ABF=∠C=45°,∠BAF=∠CAD,
∴∠FAD=∠BAF+∠BAD=∠CAD+∠BAD=∠BAC=90°,
故②正确;
由旋转可知CD=BF,
∴BE+DC=BE+BF>EF.
∵DE=EF,
∴BE+CD>DE.
故③错误;
∵∠EBF=∠ABF+∠ABC=90°,
∴在Rt△BEF中,BE2+BF2=EF2,
∵△AED≌△AEF(SAS);
∴DE=EF,
∴BE2+CD2=DE2,
故④正确,
综上,正确的为①②④.
故答案为:①②④.
44.【答案】;6.
【解答】解:(1)根据题意得:联立得,,
解得;;
∴;
故答案为:;
(2)∵将两个函数图象向右平移m个单位,
∴,
∴,,
当O、C、D三点共线时,|OC﹣OD|最小,
∴设O、C、D所在直线为正比例函数y=kx,
将点代入得:
,
解得:m=6,
故答案为:6.
45.【答案】﹣9.
【解答】解:∵点A(2,m+3),B(n,﹣4)关于y轴对称,
∴n=﹣2,m+3=﹣4,
解得m=﹣7,n=﹣2,
∴m+n=﹣7﹣2=﹣9.
故答案为:﹣9.
46.【答案】80.
【解答】解:∵AD⊥BC,
∴∠ADB=90°.
在△ABD中,∠B=30°,∠ADB=90°,
∴∠BAD=180°﹣∠B﹣∠ADB=180°﹣30°﹣90°=60°,
∴∠BAE=∠BAD﹣∠1=60°﹣25°=35°.
∵AE平分∠BAC,
∴∠BAC=2∠BAE=2×35°=70°.
在△ABC中,∠B=30°,∠BAC=70°,
∴∠C=180°﹣∠B﹣∠BAC=180°﹣30°﹣70°=80°.
故答案为:80.
47.【答案】如果两个角是对顶角,那么它们相等.
【解答】解:题设为:对顶角,结论为:相等,
故写成“如果…那么…”的形式是:如果两个角是对顶角,那么它们相等;
故答案为:如果两个角是对顶角,那么它们相等.
48.【答案】y3.
【解答】解:∵k=﹣9<0,
∴y随x增大而减小,
∵A(﹣1,y1),B(﹣0.5,y2),C(1.7,y3),﹣1<﹣0.5<1.7,
∴y1>y2>y3,
故答案为:y3.
49.【答案】﹣1.
【解答】解:∵点E的坐标为(﹣2,﹣n),其关于y轴对称的点F的坐标(2,﹣m+1),
∴﹣n=﹣m+1,
∴n﹣m=﹣1,
∴(n﹣m)2023=(﹣1)2023=﹣1.
故答案为:﹣1.
50.【答案】10.
【解答】解:∵在两个全等的三角形中,已知一个三角形的三个内角为30°,α,β(α>β),另一个三角形有一个角为70°,
∴α=70°或β=70°,
当α=70°,β=80°,
∵α>β,
∴这种情况不存在,
当β=70°,α=80°,
∴α﹣β=80°﹣70°=10°,
故答案为:10.
51.【答案】见试题解答内容
【解答】解:过O作OE⊥AB于点E,
∵BO平分∠ABD,OD⊥BC于点D,
∴OD=OE=5,
∴△AOB的面积=,
故答案为:15.
52.【答案】50.
【解答】解:把(12,600)代入y=k1x得:k1==50;
把(20,600),(28,1400)代入y=k2x+b得:
,
解得,
∴k2﹣k1=100﹣50=50.
故答案为:50.
53.【答案】.
【解答】解:∵(x1﹣x2)(y1﹣y2)<0,
∵(x1﹣x2)>0,(y1﹣y2)<0,或(x1﹣x2)<0,(y1﹣y2)>0.
∴x1>x2,y1<y2,或x1<x2,y1>y2.
即y随x的增大而减小或y随x的减小而增大.
∴2﹣5a<0.
∴.
故答案为:.
54.【答案】见试题解答内容
【解答】解:如图所示:
由平移的性质可知:∠2=∠3.
又∵∠1=∠2,
∴∠3=∠1.
∴EF∥l(内错角相等,两直线平行).
故答案为:内错角相等,两直线平行.
55.【答案】x=1.
【解答】解:原方程去分母得:6x=x+5,
解得:x=1,
检验:将x=1代入2x(x+5)得2×1×6=12≠0,
故原方程的解为x=1,
故答案为:x=1.
56.【答案】x≠2.
【解答】解:要使分式有意义,
则x﹣2≠0,
解得,x≠2,
故答案为:x≠2.
57.【答案】见试题解答内容
【解答】解:作CH⊥AB于H,连接OH,如图,
∵AC=BC=25,AB=14,
∴AH=BH=AB=7,
在Rt△BCH中,CH===24,
∵OC≥CH﹣OH(当点C、O、H共线时取等号),
∴OC的最小值为24﹣7=17.
故答案为:17.
58.【答案】见试题解答内容
【解答】解:当该等腰三角形的腰长是3时,根据韦达定理知
3+x2=4,
∴x2=1,
∴x1 x2=3=k,即k=3;
当该等腰三角形的腰长不是3时,Δ=16﹣4k=0,
解得,k=4;
综上所述,k=3或k=4.
故答案为:3或4.
59.【答案】5x>1.
【解答】解:“x的5倍大于1”,可表示为5x>1,
故答案为:5x>1.
60.【答案】10.
【解答】解:连接A′B′,如图,
∵点O分别是AA′、BB′的中点,
∴OA=OA′,OB=OB′,
在△AOB和△A′OB′中,
,
∴△AOB≌△A′OB′(SAS).
∴A′B′=AB,
∵A'B'=10cm,
∴AB=10cm,
故答案为:10.
声明:
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
