专题03 解答题(含解析)-2024-2025学年浙江地区八年级数学上学期期末备考真题分类汇编
文档属性
| 名称 | 专题03 解答题(含解析)-2024-2025学年浙江地区八年级数学上学期期末备考真题分类汇编 |  | |
| 格式 | doc | ||
| 文件大小 | 5.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-08 08:01:24 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
专题03 解答题
一.解答题(共50小题)
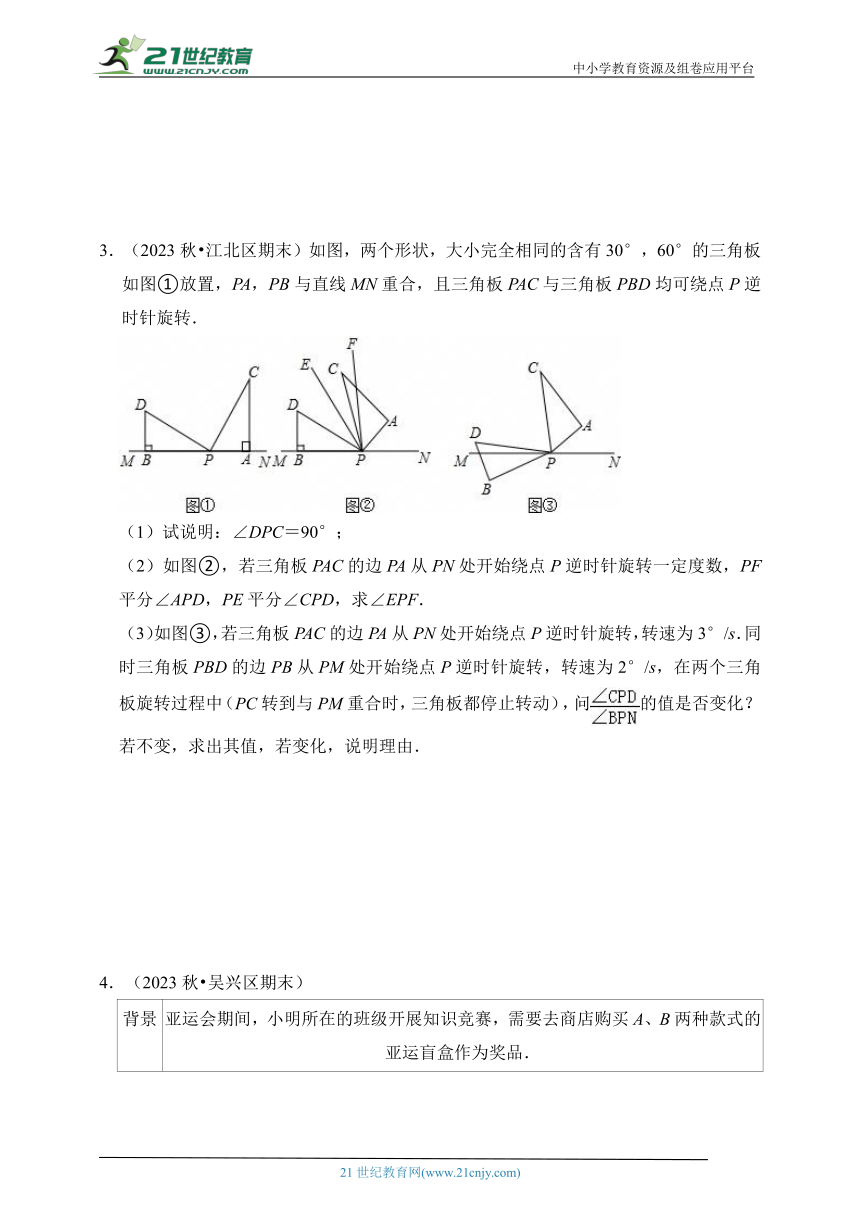
1.(2023秋 瓯海区校级期末)如图,△ABC是边长为6cm的等边三角形,点P,Q分别从顶点A,B同时出发,点P沿射线AB运动,点Q沿折线BC﹣CA运动,且它们的速度都为1cm/s.当点Q到达点A时,点P随之停止运动.连接PQ,PC,设点P的运动时间为t(s).
(1)当点Q在线段BC上运动时,BQ的长为 (cm),BP的长为 (cm)(用含t的式子表示);
(2)当PQ与△ABC的一条边垂直时,求t的值;
(3)在点Q从点C运动到点A的过程中,连接PQ,直接写出PQ中点O经过的路径长.
2.(2023秋 长兴县期末)如图,在△ABC中,AB=AC,过BC的中点D作DE⊥AB,DF⊥AC,垂足分别为点E、F.
(1)求证:DE=DF;
(2)若∠BDE=55°,求∠BAC的度数.
3.(2023秋 江北区期末)如图,两个形状,大小完全相同的含有30°,60°的三角板如图①放置,PA,PB与直线MN重合,且三角板PAC与三角板PBD均可绕点P逆时针旋转.
(1)试说明:∠DPC=90°;
(2)如图②,若三角板PAC的边PA从PN处开始绕点P逆时针旋转一定度数,PF平分∠APD,PE平分∠CPD,求∠EPF.
(3)如图③,若三角板PAC的边PA从PN处开始绕点P逆时针旋转,转速为3°/s.同时三角板PBD的边PB从PM处开始绕点P逆时针旋转,转速为2°/s,在两个三角板旋转过程中(PC转到与PM重合时,三角板都停止转动),问的值是否变化?若不变,求出其值,若变化,说明理由.
4.(2023秋 吴兴区期末)
背景 亚运会期间,小明所在的班级开展知识竞赛,需要去商店购买A、B两种款式的亚运盲盒作为奖品.
素材1 某商店在无促销活动时,若买15个A款亚运盲盒、10个B款亚运盲盒,共需230元;若买25个A款亚运盲盒、25个B款亚运盲盒,共需450元.
素材2 该商店龙年迎新春促销活动:用35元购买会员卡成为会员后,凭会员卡购买商店内任何商品,一律按商品价格的8折出售(已知小明在此之前不是该商店的会员);线上淘宝店促销活动:购买商店内任何商品,一律按商品价格的9折出售且包邮.
问题解决
任务1 某商店在无促销活动时,求A款亚运盲盒和B款亚运盲盒的销售单价各是多少元?
任务2 小明计划在促销期间购买A、B两款盲盒共40个,其中A款盲盒m个(0<m<40),若在线下商店购买,共需要 元;若在线上淘宝店购买,共需要 元.(均用含m的代数式表示)
任务3 请你帮小明算一算,在任务2的条件下,购买A款盲盒的数量在什么范围内时,线下购买方式更合算?
5.(2023秋 浦江县期末)如图,在四边形ABCD中,∠B=∠D=90°,点E,F分别在AB,AD上,AE=AF,CE=CF,求证:CB=CD.
6.(2023秋 吴兴区期末)如图,在△ABC中,E是AB上一点,AC与DE相交于点F,F是AC的中点,AB∥CD.
(1)求证:△AEF≌△CDF;
(2)若AB=10,CD=7,求BE的长.
7.(2023秋 北仑区期末)根据以下素材,探索完成任务.
如何确定拍照打卡板
素材一 设计师小聪为某商场设计拍照打卡板(如图1),图2为其平面设计图.该打卡板是轴对称图形,由长方形DEFG和等腰三角形ABC组成,且点B,F,G,C四点共线.其中,点A到BC的距离为1.2米,FG=0.8米,DG=1.5米.
素材二 因考虑牢固耐用,小聪打算选用甲、乙两种材料分别制作长方形DEFG与等腰三角形ABC(两种图形无缝隙拼接),且甲材料的单价为85元/平方米,乙材料的单价为100元/平方米.
问题解决
任务一 推理最大高度 小聪说:“如果我设计的方案中CB长与C,D两点间的距离相等,那么最高点B到地面的距离就是线段DG长”,他的说法对吗?请判断并说明理由.
任务二 探究等腰三角形ABC面积 假设CG长度为x米,等腰三角形ABC的面积为S.求S关于x的函数表达式.
任务三 确定拍照打卡板 小聪发现他设计的方案中,制作拍照打卡板的总费用不超过180元,请你确定CG长度的最大值.
8.(2023秋 滨江区期末)如图,在△ABC中,∠ABC=45°,CD⊥AB于点D,BE⊥AC于点E,CD与BE相交于点F.
(1)求证:BF=AC;
(2)若∠A=60°,△ADC的中线DG=1,求BC的长.
9.(2023秋 莲都区期末)已知一次函数y=kx+b的图象经过点A(﹣1,3)和点B(1,﹣1).
(1)求此一次函数的表达式;
(2)若点C(a,2)向右平移3个单位后恰好落在直线AB上,求a的值.
10.(2023秋 莲都区期末)如图,∠A=∠D,∠B=∠E,AF=CD.
(1)求证:△ABC≌△DEF;
(2)若∠A=20°,∠E=75°,求∠BCF的度数.
11.(2023秋 滨江区期末)如图,为了测量一条两岸平行的河流宽度,由于跨河测量困难,所以,三个数学研究小组设计了不同的方案,他们在河南岸的点B处,测得河北岸的一棵树底部A点恰好在点B的正北方向,测量方案如下表:
课题 测量河流宽度
工具 测量角度的仪器(仪器的高度忽略不计),标杆,皮尺等
小组 第一小组 第二小组 第三小组
测量方案 观测者从B点向正东走到C点,此时恰好测得:∠ACB=45° 观测者从B点向正东走到E点,O是BE的中点,继续从点E沿垂直于BE的EF方向走,直到点A,O,F在一条直线上.
测量示意图
(1)第一小组认为,河宽AB的长度就是线段 的长度.
(2)第二小组方案灵感来源于古希腊哲学家泰勒斯,他们认为只要测得EF的长就是所求河宽AB的长,你认为第二小组的方案可行吗?如果可行,请给出证明;如果不可行,请说明理由.
(3)请你代表第三小组,设计一个测量方案,把测量方案和测量示意图填入上表,然后指明你画的示意图中,只要测出哪条线段的长,就能推算出河宽AB长,并说明方案的可行性.
12.(2023秋 莲都区期末)如图,直线m的函数表达式为y=﹣2x﹣6,与x轴交于点A,直线n经过点B(2,0)和点C(0,﹣1),且直线m,n交于点D.
(1)求点A,点D的坐标.
(2)点P是x轴上的一个动点,求PA+PB+PC+PD的最小值.
(3)点M,N分别是直线m,n上的两点,且不与点A,B重合.当△MND≌△BAD时,直接写出每一组点M和点N的坐标.
13.(2023秋 长兴县期末)如图,在△ABC中,AB=AC,过CA的延长线上一点D,作DE⊥BC,垂足为E,交边AB于点F.
(1)求证:△ADF是等腰三角形;
(2)若AD=13,BE=5,F为AB的中点,求EF的长.
14.(2023秋 鄞州区期末)在平面直角坐标系中,O为原点,点A(0,3),B(﹣4,0),C(4,0).若将点B向右平移10个单位长度,再向上平移4个单位长度,得到对应点D.
(1)点D的坐标为 ;
(2)若点P是y轴上一动点,若△PAC的面积等于△CAD的面积,请求出点P的坐标;
(3)若点E为x轴上一动点,若△EAC为等腰三角形,请直接写出点E的坐标.
15.(2023秋 余姚市期末)如图,在△ABC中,AB=AC=5,BC=6,点D在AC边上,BD=AB.(1)求△ABC的面积;
(2)求AD的长.
16.(2023秋 鄞州区期末)【基础练习】
(1)如图1,在等腰Rt△ABC中,∠C=90°,AC=1,AD平分∠BAC交BC于点D,DE⊥AB于点E,求BE的长.
【类比探究】
(2)如图2,AD是△ABC的角平分线,∠B=40°,∠C=80°,点E在AB上,AE=AC.求证:AB=AC+CD.
【拓展延伸】
(3)如图3,点P是等边△ABC外一点,连结PA,PC,PB,恰好满足PA=AB.AD平分∠PAB交PC于点D,线段AD,CD,PD之间有什么关系?请作出猜测并进行证明.
17.(2023秋 北仑区期末)如图,已知AB=AD,∠BAD=∠CAE,∠B=∠D,AD与BC交于点P,点C在DE上.
(1)求证:AC=AE;
(2)若∠B=36°,∠APC=72°.
①求∠E的度数;
②求证:CP=CE.
18.(2023秋 瓯海区校级期末)如图,点A、C、D、B在同一条直线上,点E、F分别在直线AB的两侧,AE=BF,CE=DF,AD=BC.
(1)求证:△ACE≌△BDF.
(2)若∠CDF=55°,求∠ACE的度数.
19.(2023秋 海曙区校级期末)如图,点B、C、D在同一条直线上,AB⊥BD,DE⊥BD,AC⊥CE,AB=CD.
(1)求证:△ABC≌△CDE.
(2)若∠ACB=37°,求∠AED的度数.
20.(2023秋 东阳市期末)我们新定义一种三角形:若一个三角形中存在两边的平方差等于第三边上高的平方,则称这个三角形为勾股高三角形,两边交点为勾股顶点.
●特例感知
①等腰直角三角形 勾股高三角形(请填写“是”或者“不是”);
②如图1,已知△ABC为勾股高三角形,其中C为勾股顶点,CD是AB边上的高.若BD=2AD=2,试求线段CD的长度.
●深入探究
如图2,已知△ABC为勾股高三角形,其中C为勾股顶点且CA>CB,CD是AB边上的高.试探究线段AD与CB的数量关系,并给予证明;
●推广应用
如图3,等腰△ABC为勾股高三角形,其中AB=AC>BC,CD为AB边上的高,过点D向BC边引平行线与AC边交于点E.若CE=a,试求线段DE的长度.
(2023秋 鄞州区期末)解方程:.
22.(2023秋 鄞州区期末)如图,在两个完全相同的甲、乙容器中,最初,容器甲有10cm高的水,容器乙放了一个长方体,且容器底面积是长方体底面积的4倍.从甲容器向乙容器用虹吸原理注水(虹吸装置的体积忽略不计),当注满时,容器乙中液面与长方体上底面相平.设容器甲中的液面高为y1(单位:cm),容器乙中的液面高为y2(单位:cm).小科绘制了y1、y2关于时间x(单位:s)的函数图象如图2所示.回答下列问题:
(1)a的值为 ;容器甲的液面下降速度是 cm/s:
(2)求b的值以及y2关于x的函数表达式;
(3)当容器甲中的液面高y1与容器乙中的液面高y2相差2cm时,求此时x的值.
23.(2023秋 鄞州区期末)如图,在△ABC中,,∠BAC=90°,AD⊥BC,E在AC边上运动(不与点A重合),AE<CE,将△CDE沿DE折叠至△FDE,EF分别与AD,AB交于G,H两点.
(1)求证:∠BDF=2∠ADE;
(2)如图1,若DG=3AG,求△AGE的周长;
(3)如图2,设DF与AB交于点M,在整个运动过程中,记△FMH与△AEG的周长之和为y,则y的值是否变化,若变化求出范围;若不变,求出y.
24.(2023秋 鄞州区期末)【阅读材料】小明在兴趣小组学习了“基本不等式”的相关知识.整理如下:对于正数a、b,有,所以a+b﹣2≥0,即a+b≥2(当且仅当a=b时取到等号)特别地,a+=2(当且仅当a=1时取到等号),因此,当a>0时,a+有最小值2,此时a=1.
【简单应用】小明完成了大部分老师布置的作业,但还有两题不会,请你帮一帮他.
(1)函数y=2﹣x﹣(x>0)的最大值为 .
(2)求函数y=4x+(x>1)的最小值,并写出取最小值时x的值.
【猜想提升】小明由上述的a+b≥2提出猜想:a+b+c≥3(当且仅当a=b=c时取到等号).通过查阅资料,他惊奇地发现这个猜想是正确的,请你利用小明这个猜想解答下面的问题.
设a,b,c是非负实数,求的最小值.
25.(2023秋 鄞州区期末)(1)已知a、b是方程x2﹣4x+1=0的两个根,求的值.
(2)已知a、b、c均为实数,且a+b+c=2,ab+c=c2,求正数c的最大值.
26.(2022秋 拱墅区校级期末)如图,在△ABC中,∠C=∠ABC=2∠A,BD是AC边上的高,求∠DBC的度数.
27.(2023秋 慈溪市期末)如图,已知△ABC和△CDE均为等边三角形,点D在AB的延长线上,连结AE.
(1)求证:△ACE≌△BCD;
(2)求∠DAE的度数.
28.(2023秋 台州期末)如图,在平面直角坐标系中,A(﹣2,4),B(﹣4,1),C(﹣1,2).
(1)在图中画出△ABC关于y轴的对称图形△A1B1C1,并写出点A1,B1,C1的坐标;
(2)请在x轴上画出点P的位置,使得PB+PC最短,并直接写出点P的坐标.
29.(2023秋 台州期末)如图,在△ABC中,∠BAC=80°,∠B=60°,AD是BC边上的高,∠ACB的平分线CF交AD于点E.求∠AEC的度数.
30.(2023秋 台州期末)如图,点A,F,C,D在同一条直线上,AF=CD,∠A=∠D,BC∥EF.求证:BC=EF.
31.(2023秋 镇海区校级期末)近年来,电商平台直播带货成了一个火热的新兴职业,某主播带货图书《苏东坡传》,他用双语直播,风趣幽默,点燃了不同年龄者的读书热情.已知这本书的成本价为10元,规定销售单价不低于成本价,且不高于成本价的3倍,通过前几天的销售发现,该书每天的销售量y(本)与销售单价x(元/本)之间近似满足一次函数关系,部分对应数据如表:
x(元/本) … 15 25 …
y(本) … 700 500 …
(1)根据表格提供的数据,求y关于x的函数关系式,并写出x的取值范围.
(2)若销售该书每天的利润为6000元,求该书的销售单价.
(3)销售该书每天的利润能否达到9000元?请说明理由.
32.(2023秋 鄞州区期末)为迎接新春佳节的到来,一水果店计划购进甲、乙两种新出产的水果共160千克,这两种水果的进价、售价如表所示:
进价(元/千克) 售价(元/千克)
甲种 5 8
乙种 9 13
(1)若该水果店预计进货款为1000元,则这两种水果各购进多少千克?
(2)若该水果店决定乙种水果的进货量不超过甲种水果的进货量的3倍,应怎样安排进货才能使水果店在销售完这批水果时获利最多?此时利润为多少元?
33.(2023秋 上城区期末)一次函数y1=ax+b(a≠0)恒过定点(1,0).
(1)若一次函数y1=ax+b还经过(2,3)点,求y1的表达式;
(2)若有另一个一次函数y2=bx+a.
①点A(m,p)和点B(n,p)分别在一次函数y1和y2的图象上,求证:m+n=2;
②设函数y=y1﹣y2,当﹣2≤x≤4时,函数y有最大值6,求a的值.
34.(2023秋 南浔区期末)【问题背景】新能源汽车多数采用电能作为动力来源,不需要燃烧汽油,这样就减少了二氧化碳等气体的排放,从而达到保护环境的目的.
【实验操作】
为了解汽车电池需要多久能充满,以及充满电量状态下汽车的最大行驶里程,某综合实践小组设计两组实验,实验一:探究电池充电状态下汽车仪表盘显示电量y1(%)与时间t(小时)的关系,数据记录如表1.
实验二:探究充满电量状态下汽车行驶过程中仪表盘显示电量y2(%)与行驶里程s(千米)的关系,数据记录如表2.
电池充电状态
时间t(小时) 0.5 1 1.5 2
电量y1(%) 25 50 75 100
表1
汽车行驶过程
已行驶里程s(千米) 0 80 100 140
电量y2(%) 100 60 50 30
表2
任务一:计算表1中每隔0.5小时电池电量的增加量;
【建立模型】
任务二:请结合表1、表2的数据,选择合适的数学模型,求出y1关于t的函数表达式及y2关于s的函数表达式;
【解决问题】
任务三:某电动汽车在充满电量的状态下出发,前往距离出发点250千米处的目的地,若电动车平均每小时行驶40千米,行驶3小时后,在途中的服务区充电,一次性充电若干时间后汽车以原速度继续行驶,若要保证司机在最短的时间快速到达目的地,则至少要在服务区充电多长时间?
35.(2023秋 台州期末)如图,在正方形网格中,点A,B,C均为网格线交点,请按要求作图,作图过程仅使用无刻度的直尺,保留作图痕迹,无需说明理由.
(1)如图1,作出△ABC关于直线MN对称的图形;
(2)如图2,在直线MN上求作点P,使得∠APM=∠BPN.
36.(2023秋 西湖区期末)如图,在△ABC中,AD是BC边上的高线,CE是AB边上的中线,AD与CE交于点F,点G为CE的中点,CD=AE.
(1)求证:DG⊥CE.
(2)若AF=EF,求∠B的度数.
37.(2023秋 江北区期末)在菱形ABCD中,过点B作BE⊥CD于点E,点F在边AB上,AF=CE,连接BD、DF.
(1)求证:四边形BFDE是矩形;
(2)若BD=2,BE=4,求BC的长.
38.(2023秋 江北区期末)宾馆有50间房供游客居住,当每间房每天定价为180元时宾馆会住满;当每间房每天的定价加10元时,就会空一间房,如果有游客居住,宾馆还需对居住的每间房每天支出20元的费用.
(1)当定价为200元时,会空 间房,每天的利润是 元.
(2)若宾馆每天想获得的利润为10890元,应该将每间房每天定价为多少元?
39.(2023秋 路桥区期末)如图,在△ABC中,BD平分∠ABC,AE⊥BC于点E,交BD于点F.若∠ABC=48°,求∠AFB的度数.
40.(2023秋 江北区期末)如图,∠ACB=90°,AC=BC,AD⊥MN,BE⊥MN,垂足分别是D,E.
(1)求证:△ADC≌△CEB;
(2)猜想线段AD,BE,DE之间具有怎样的数量关系,并说明理由.
(2023秋 余姚市期末)解一元一次不等式组:.
42.(2023秋 舟山期末)解不等式组,并将解集在数轴上表示出来.
43.(2023秋 江北区期末)现有一段20千米长,可供长跑爱好者跑步的笔直跑道MN,已知甲、乙两人都从M点出发,甲跑到途中的P点后原地休息了20分钟,之后继续跑到N点,共用时间2小时;乙虽然比甲晚出发半小时,但和甲同时到达N点.假设两人跑步时均为匀速,在甲出发后的2小时内两人离开M点的距离y(千米)与时间x(小时)的函数关系如图所示.请回答下列问题:
(1)图中B点的坐标为
(2)甲从点P跑到点N的速度为 千米/时;
(3)求图中线段CD的表达式.并写出定义域.
44.(2023秋 江北区期末)如图,在正方形ABCD中,若P是AD上一点,点A关于直线BP的对称点E,连结CE,且CE的延长线交BP延长线于点F,连结DE.
(1)若∠ABP=25°,求∠FCB和∠F的度数.
(2)若P是AD中点;
①求证:DE∥BF;
②若AB=6时,直接写出CF的长.
45.(2023秋 宁波期末)如图,在△ABC中,∠ACB=90°,点E,F在边AB上,将边AC沿CE翻折,使点A落在AB上的点D处,再将边BC沿CF翻折,使点B落在CD的延长线上的点B'处.
(1)求∠ECF的度数;
(2)若CE=4,B'F=1,求线段BC的长和△ABC的面积.
46.(2023秋 鄞州区校级期末)“低碳环保,绿色出行”的理念得到广大群众的接受,越来越多的人喜欢选择自行车作为出行工具.小军和爸爸同时从家骑自行车去图书馆,爸爸先以150米/分的速度骑行一段时间,休息了5分钟,再以m米/分的速度到达图书馆,小军始终以同一速度骑行,两人行驶的路程y(米)与时间x(分钟)的关系如图,请结合图象,解答下列问题:
(1)a= ,b= ,m= ;
(2)若小军的速度是120米/分,求小军在途中与爸爸第二次相遇时,距图书馆的距离;
(3)在(2)的条件下,爸爸自第二次出发后至到达图书馆前,何时与小军相距100米,请求出此时小军骑行的时间.(直接写出答案)
47.(2023秋 瓯海区校级期末)已知一次函数的图象经过点A(1,8)和点B(﹣3,0),
(1)求这个一次函数的解析式;
(2)判断点(﹣1,5)在不在该图象上,并说明理由.
48.(2023秋 东阳市期末)在△ABC中,AD是高,AE,BF是角平分线,AE交BF于点O,∠BAC=80°,∠C=70°.
(1)求∠BOE的大小;
(2)求证:DE=DC.
49.(2023秋 瓯海区校级期末)如图1,图2都是4×4的正方形网格,每个小正方形的顶点称为格点.如图,线段AB的两端点均在格点上,在给定的网格中,按下列要求用无刻度的直尺画等腰△ABC,使点C在格点上.
(1)在图1中,画以AB为腰的三角形;
(2)在图2中,画以AB为底的三角形.
50.(2023秋 上城区期末)综合与实践
生活中的数学:如何确定单肩包最佳背带长度
素材1 如图是一款单肩包,背带由双层部分、单层部分和调节扣构成.使用时可以通过调节扣加长或缩短单层部分的长度,使背带的总长度加长或缩短(总长度为单层部分与双层部分的长度和,其中调节扣的长度忽略不计).
素材2 对于该背包的背带长度进行测量,设双层的部分长度是x cm,单层部分的长度是y cm,得到如下数据:双层部分长度x(cm)261014a单层部分长度y(cm)1161081009270
素材3 单肩包的最佳背带总长度与身高比例为2:3
素材4 小明爸爸准备购买此款背包.爸爸自然站立,将该背包的背带调节到最短提在手上,背带在背包的悬挂点离地面的高度为53.5cm;已知爸爸的臂展和身高一样,且肩宽为38cm,头顶到肩膀的垂直高度为总身高的.
任务1 在平面直角坐标系中,以所测得数据中的x为横坐标,以y为纵坐标,描出所表示的点,并用光滑曲线连接,根据图象思考变量x、y是否满足一次函数关系.如果是,求出该函数的表达式,直接写出a值并确定x的取值范围.
任务2 设人身高为h,当单肩包背带长度调整为最佳背带总长度时,求此时人身高h与这款背包的背带双层部分的长度x之间的函数表达式.
任务3 当小明爸爸的单肩包背带长度调整为最佳背带总长度时.求此时双层部分的长度.
参考答案与试题解析
一.解答题(共50小题)
1.【答案】(1)t,6﹣t;
(2)满足条件的t的值为2或4或8.
(3)3cm.
【解答】解:(1)由题意BQ=t cm,PB=(6﹣t)cm.
故答案为:t,6﹣t;
(2)如图1中,当PQ⊥BC时,
∵∠PQB=90°,∠B=60°,
∴∠BPQ=30°,
∴PB=2BQ,
∴6﹣t=2t,
∴t=2.
如图2中,当QP⊥AB时,同法可得QB=2PB,
∴t=2(6﹣t),
∴t=4.
如图3中,当PQ⊥AC时,同法可得AP=2AQ,
∴t=2(12﹣t),
∴t=8,
综上所述,满足条件的t的值为2或4或8.
(3)如图,过Q作QH∥BC交AB于H,
则△AHQ是等边三角形,
∴AQ=AH,
∵AC=AB,
∴CQ=BH,
∵CQ=BP,
∴BH=BP,
∴QE=PE,
∴点E是PQ的中点,
∴在点Q从点C运动到点A的过程中,连接PQ,PQ中点O经过的路径长为BC=3(cm).
2.【答案】(1)证明见解答;(2)∠BAC=110°.
【解答】(1)证明:连接AD,
∵D是BC的中点,AB=AC,
∴AD平分∠BAC,
∵DE⊥AB,DF⊥AC,
∴DE=DF;
(2)解:∵DE⊥AB,
∴∠BED=90°,
∵∠BDE=55°,
∴∠B=35°,
∴∠C=35°,
∴∠BAC=110°.
3.【答案】见试题解答内容
【解答】解:(1)∵∠DPC=180°﹣∠CPA﹣∠DPB,∠CPA=60°,∠DPB=30°,
∴∠DPC=180°﹣30°﹣60°=90°;
(2)设∠CPE=∠DPE=x,∠CPF=y,
则∠APF=∠DPF=2x+y,
∵∠CPA=60°,
∴y+2x+y=60°,
∴x+y=30°
∴∠EPF=x+y=30°
(3)不变.
设运动时间为t秒,则∠BPM=2t,
∴∠BPN=180﹣2t,∠APN=3t.
∴∠CPD=360﹣∠DPB﹣∠BPN﹣∠CPA﹣∠APN=90﹣t,
∴==.
4.【答案】(任务1)该商店在无促销活动时,A款亚运盲盒的销售单价是10元,B款亚运盲盒的销售单价是8元;
(任务2)(1.6m+291),(1.8m+288);
(任务3)当购买A款盲盒的数量超过15个且少于40个时,线下购买方式更合算.
【解答】解:(任务1)设该商店在无促销活动时,A款亚运盲盒的销售单价是x元,B款亚运盲盒的销售单价是y元,
根据题意得:,
解得:.
答:该商店在无促销活动时,A款亚运盲盒的销售单价是10元,B款亚运盲盒的销售单价是8元;
(任务2)根据题意得:在线下商店购买,共需要35+10×0.8m+8×0.8(40﹣m)=(1.6m+291)(元);
在线上淘宝店购买,共需要10×0.9m+8×0.9(40﹣m)=(1.8m+288)(元).
故答案为:(1.6m+291),(1.8m+288);
(任务3)根据题意得:1.6m+291<1.8m+288,
解得:m>15,
又∵0<m<40,
∴15<m<40.
答:当购买A款盲盒的数量超过15个且少于40个时,线下购买方式更合算.
5.【答案】见试题解答内容
【解答】证明:如图,连接AC,
在△ACE和△ACF中,
,
∴△ACE≌△ACF(SSS),
∴∠EAC=∠FAC,
∵∠B=∠D=90°,
∴CB=CD.
6.【答案】(1)证明见解答;
(2)3.
【解答】(1)证明:∵AB∥CD,
∴∠A=∠DCF,
∵点F是AC的中点,
∴AF=CF,
在△AEF和△CDF中,
,
∴△AEF≌△CDF(ASA),
(2)解:由(1)得:△AEF≌△CDF,
∴AE=CD,
∵AB=10,CD=7,
∴BE=AB﹣AE=AB﹣CD=10﹣7=3.
7.【答案】见试题解答内容
【解答】解:任务1:他的说法对,理由如下:
如图:过点B作BH⊥DC于点H,
∴∠BHC=90°.
∵四边形EFGD是长方形,
∴∠DGC=90°.
∴∠BHC=∠DGC,
在△BCH与△DCG中,
,
∴△BCH≌△DCG(AAS),
∴BH=DG.
∴最高点B到地面的距离就是线段DG长.
任务2:∵该指示牌是轴对称图形,四边形EFHD是长方形,
∴设BF=CG=x,则BC=2x+0.8.
又△ABC的高为1.2米,
∴三角形ABC的面积S=×(2x+0.8)×1.2=1.2x+0.48.
任务3:由题意,当长方形用甲种材料制作,三角形用乙种材料制作时,
又长方形的面积为:DH DE=0.8×1.5=1.2(平方米),
∴1.2×85+(1.2x+0.48)×100≤180.
解得x≤0.25,
故CG长度的最大值为0.25米.
8.【答案】(1)证明见解答过程;
(2).
【解答】(1)证明:∵CD⊥AB,
∴∠CDA=∠BDF=90°,
∴∠DBF+∠DFB=180°﹣∠BDF=90°,
又∵BE⊥AC,
∴∠BEA=90°,
∴∠DBF+∠DAC=180°﹣∠BEA=90°,
∴∠DAC=∠DFB,
又∵∠ABC=45°,
∴∠DCB=180°﹣∠ABC﹣∠BDF=45°=∠ABC,
∴BD=CD,
在△ACD和△FBD中,
,
∴△ACD≌△FBD(AAS),
∴AC=BF;
(2)解:如图,
在Rt△ACD中,中线DG=1,
∴AC=2DG=2,
∵∠A=60°,∠ADC=90°,
∴∠ACD=30°,
∴AD=AC=1,
∴CD===BD,
∴BC==.
9.【答案】(1)y=﹣2x+1;
(2).
【解答】解:(1)将点A(﹣1,3)和点B(1,﹣1)代入y=kx+b,
得,
解得:k=﹣2,b=1,
∴一次函数的表达式为y=﹣2x+1;
(2)点C(a,2)向右平移3个单位后坐标为(a+3,2),
∵点(a+3,2)在直线AB上,
∴2=﹣2(a+3)+1,
解得:.
10.【答案】(1)证明见解析;
(2)95°.
【解答】(1)证明:∵AF=CD,
∴AF﹣CF=CD﹣CF,
即AC=DF,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(AAS);
(2)解:∵∠B=∠E,∠E=75°
∴∠B=75°,
∵∠BCF是△ABC的一个外角,
∴∠BCF=∠A+∠B,
∵∠A=20°,
∴∠BCF=20°+75°=95°.
11.【答案】见试题解答内容
【解答】解:(1)∵AB⊥BC,∠ACB=45°,
∴△ABC是等腰直角三角形,
∴BC=AB,
∴河宽AB的长度就是线段BC的长度.
故答案为:BC;
(2)第二小组的方案可行,理由如下:
∵O是BE中点,
∴OB=OE,
∵AB⊥BE,EF⊥BE,
∴∠ABO=∠FEO=90°,
在△ABO和△FEO中,
,
∴△ABO≌△FEO(ASA),
∴EF=AB,
∴河宽AB的长度就是线段EF的长度.
(3)见表格,
课题 测量河流宽度
工具 测量角度的仪器(仪器的高度忽略不计),标杆,皮尺等
小组 第一小组 第二小组 第三小组
测量方案 观测者从B点向正东走到C点,此时恰好测得:∠ACB=45° 观测者从B点向正东走到E点,O是BE的中点,继续从点E沿垂直于BE的EF方向走,直到点A,O,F在一条直线上. 观测者从B点向正西走到C点,使用测量角度的仪器测得∠BCD=∠ACB=65°,CD交AB延长线于D,
测量示意图
只要测出BD的长,就能推算出河宽AB长,理由如下:
∵AB⊥BC,
∴∠ABC=∠DBC=90°,
在△ABC和△DBC中,
,
∴△ABC≌△DBC(ASA),
∴BD=AB,
∴河宽AB的长等于线段BD的长.
12.【答案】见试题解答内容
【解答】解:(1)∵直线m的函数表达式为y=﹣2x﹣6,与x轴交于点A,
令y=0,可得0=﹣2x﹣6,解得x=﹣3,
∴A(﹣3,0),
设直线n的解析式为y=kx+b,
∵直线n经过点B(2,0)和点C(0,﹣1),
∴,解得,
∴直线n的解析式为y=x﹣1,
联立y=﹣2x﹣6得,解得,
∴点D的坐标为(﹣2,﹣2);
(2)作点C关于x轴的对称点E,连接DE交x轴于点P,连接CP,
∴PE=PC,E(0,1),
∴PC+PD=PD+PE,此时PC+PD=DE最小,PA+PB=AB最小,
∵点D的坐标为(﹣2,﹣2),A(﹣3,0),B(2,0),
∴DE==,AB=2+3=5,
∴PA+PB+PC+PD的最小值为5+;
(3)∵点D的坐标为(﹣2,﹣2),A(﹣3,0),点D的坐标为(﹣2,﹣2);
∴AB=2+3=5,AD==,BD==2,
设M(m,﹣2m﹣6),N(n,n﹣1),
当△MND≌△BAD时,ND=AD=,MD=BD=2,
∴=2,=,
解得m=0或﹣4,n=0或﹣4,
∴点M和点N的坐标分别为(﹣4,2)、(0,﹣1)或(0,﹣6)、(0,﹣1)或(﹣4,2)、(﹣4,﹣3)或(0,﹣6)、(﹣4,﹣3).
13.【答案】见试题解答内容
【解答】解:(1)证明:∵在△ABC中,AB=AC,
∴∠B=∠C,
∵DE⊥BC,
∴∠B+∠BFE=90°,∠C+∠D=90°,
∴∠BFE=∠D,
又∵∠BFE=∠AFD,
∴∠D=∠AFD,
∴△ADF 是等腰三角形;
(2)∵F为AB的中点,
∴AF=BF,
∵△ADF是等腰三角形,
BF=AF=AD=13,
∵DE⊥BC,
∴EF==12,
答:EF的长为12.
14.【答案】(1)(6,4);
(2)(0,)或(0,﹣);
(3)(,0)或(﹣4,0)或(﹣1,0)或(9,0).
【解答】解:(1)∵B(﹣4,0),将点B向右平移10个单位长度,再向上平移4个单位长度,得到对应点D.
∴D的坐标为(﹣4+10,0+4)即D的坐标为:(6,4);
故答案为:(6,4);
(2)设点P(0,a),
△CAD的面积为4×6﹣×3×6﹣×2×4﹣×4×3=11,
△PAC的面积为×|a﹣3|×4=2|a﹣3|,
∵△PAC的面积等于△CAD的面积,
∴2|a﹣3|=11,
解得a=或﹣,
∴P的坐标为(0,)或(0,﹣);
(3)△EAC为等腰三角形,当AC为底时,点E在AC的垂直平分线上,如图:
∴AE=CE,
设OE=x,CE=AE=4﹣x,
在Rt△AOE中,32+x2=(4﹣x)2,
解得x=,
∴E的坐标为(,0);
当AC为腰时,如图,
若AE=AC=5,此时E的坐标为(﹣4,0),
若AC=AE=5,此时OE=1,E的坐标为(﹣1,0),
若AC=AE=5,此时E的坐标为(9,0),
综上所述,若△EAC为等腰三角形,点E的坐标为(,0)或(﹣4,0)或(﹣1,0)或(9,0).
15.【答案】(1)12;
(2).
【解答】解:(1)过点A作AM⊥BC于点M,
∵AB=AC,AM⊥BC,
∴M是BC的中点,
∵AB=5,BC=6,
∴BM=CM=3,
∴AM===4,
∴△ABC的面积=BC AM=×6×4=12;
(2)解法一:过点B作BN⊥AC于点N,
∵BD=AB,
∴AN=DN=AD,
∵△ABC的面积=AC BN=×5 BN=12;
∴BN=,
AN==,
∴AD=2AN=.
解法二:过点B作BN⊥AC于点N,
∵BD=AB,
∴AN=DN=AD,
设AN=x,则CN=5﹣x,
∵AB=AC,AM⊥BC,
∵BN2=AB2﹣AN2=BC2﹣CN2,
∴25﹣x2=36﹣(5﹣x)2,
∴x=,
∴AD=2AN=.
16.【答案】(1)﹣1;
(2)证明见解析;
(3)AD+PD=CD,证明见解析.
【解答】(1)解:∵△ABC是等腰直角三角形,∠C=90°,AC=1,
∴AB=AC=,
∵AD平分∠BAC,DE⊥AB,
∴DE=DC,
在Rt△ADE和Rt△ADC中,
,
∴Rt△ADE≌Rt△ADC(HL),
∴AE=AC=1,
∴BE=AC﹣AE=﹣1;
(2)证明:∵AD为△ABC的角平分线,
∴∠CAD=∠EAD,
在△AED和△ACD中,
,
∴△AED≌△ACD(SAS),
∴∠AED=∠C=80°,ED=CD,
∵∠AED=∠B+∠EDB,
∴∠EDB=∠AED﹣∠B=80°﹣40°=40°,
∴∠B=∠EDB,
∴ED=EB,
∴EB=CD,
∵AB=AE+EB,
∴AB=AC+CD;
(3)解:AD+PD=CD,证明如下:
如图3,在CD上取点E,使CE=PD,连接AE,
∵△ABC是等边三角形,
∴AB=AC,∠BAC=60°,
∵PA=AB,
∴AC=PA,
∴∠APD=∠ACE,
在△APD和△ACE中,
,
∴△APD≌△ACE(SAS),
∴AD=AE,∠PAD=∠CAE,
∵AD平分∠PAB,
∴∠PAD=∠BAD,
∴∠BAD=∠CAE,
∴∠BAD+∠BAE=∠CAE+∠BAE,
即∠DAE=∠BAC=60°,
∴△ADE是等边三角形,
∴AD=DE,
∵DE+CE=CD,
∴AD+PD=CD.
17.【答案】(1)证明见解答过程;
(2)①72°;
②证明见解答过程.
【解答】(1)证明:∵∠BAD=∠CAE,
∴∠BAD+∠DAC=∠CAE+∠DAC,
即∠BAC=∠DAE,
在△BAC和△DAE中,
,
∴△BAC≌△DAE(ASA),
∴AC=AE;
(2)①解:∵∠B=36°,∠APC=72°,
∴∠BAP=∠APC﹣∠B=72°﹣36°=36°,
∴∠CAE=36°,
∵△BAC≌△DAE,
∴AC=AE,
∴∠ACE=∠E=×(180°﹣∠CAE)=×(180°﹣36°)=72°;
②证明:∵△BAC≌△DAE,
∴∠ACB=∠E,
∴∠ACB=∠ACE,∠APC=∠E,
在△ACP和△ACE中,
,
∴△ACP≌△ACE(AAS),
∴CP=CE.
18.【答案】见试题解答内容
【解答】(1)证明:∵AD=BC,
∴AD﹣CD=BC﹣CD,
∴AC=BD;
在△ACE和△BDF中,
,
∴△ACE≌△BDF(SSS);
(2)解:由(1)可知:△ACE≌△BDF,
∴∠ACE=∠BDF,
∵∠CDF=55°,
∴∠BDF=125°=∠ACE.
19.【答案】(1)见解析过程;
(2)82.
【解答】(1)证明:∵AB⊥BD,DE⊥BD,AC⊥CE,
∴∠B=∠D=∠ACE=90°.
∴∠BAC+∠ACB=90°,∠ACB+∠DCE=90°.
∴∠BAC=∠DCE.
在△ABC和△CDE中,
,
∴△ABC≌△CDE(ASA).
(2)解:∵△ABC≌△CDE,
∴AC=CE,∠ACB=∠CED=37°,
∴∠CAE=∠AEC=45°,
∴∠AED=37°+45°=82°.
20.【答案】见试题解答内容
【解答】解:●特例感知:
① 等腰直角三角形是勾股高三角形.
故答案为:是.
②如图1中,根据勾股定理可得:CB2=CD2+4,CA2=CD2+1,
于是CD2=(CD2+4)﹣(CD2+1)=3,
∴CD=.
●深入探究:
如图2中,由CA2﹣CB2=CD2可得:CA2﹣CD2=CB2,而CA2﹣CD2=AD2,
∴AD2=CB2,
即AD=CB;
●推广应用:
过点A向ED引垂线,垂足为G,
∵“勾股高三角形”△ABC为等腰三角形,且AB=AC>BC,
∴只能是AC2﹣BC2=CD2,由上问可知AD=BC……①.
又ED∥BC,∴∠1=∠B……②.
而∠AGD=∠CDB=90°……③,
∴△AGD≌△CDB(AAS),
∴DG=BD.
易知△ADE与△ABC均为等腰三角形,
根据三线合一原理可知ED=2DG=2BD.
又AB=AC,AD=AE,
∴BD=EC=a,
∴ED=2a.
21.【答案】.
【解答】解:,
两边平方得,
整理可得,
两边平方得,
整理得,
令,
可得4t=(t+1)2,
解得t=1,
∴,
整理得x2﹣x﹣1=0
解得,
根据二次根式有意义的条件可得x≥1,
∴.
22.【答案】(1)10;1;
(2);;
(3)或.
【解答】解:(1)根据题意可得容器甲有10cm高的水,
故a=10,
根据图象可得容器甲的水10s放完,故容器甲的液面下降速度是(cm/s),
故答案为:10;1;
(2)根据图像可得b为容器甲放完水时,容器乙中水面高度,
设长方体底面积为t cm2,则容器底面积为4t cm2,
∴水的体积为4t 10=40t cm3,
容器乙实际可装水的底面积为4t﹣t=3t cm2,
∴容器乙中水面高度为,即,
设y2=kx,把代入,得:
,
解得,
∴;
(3)设y1=kx+b,把(0,10),(10,0)代入函数解析式得:
,
解得,
∴y1=﹣x+10,
①当y1﹣y2=2时,可得,
解得;
②当y2﹣y1=2时,可得,
解得x=,
∴当容器甲中的液面高y1与容器乙中的液面高y2相差2cm时,此时x的值为或.
23.【答案】(1)见解析;
(2)或;
(3)y的值是变化的,变化范围为.
【解答】(1)证明:∵AD⊥BC,
∴∠BDF+∠ADF=∠ADB=90°,
∴∠ADF=90°﹣∠BDF,
∵将△CDE沿DE折叠至△FDE,
∴∠CDE=∠EDF=∠ADE+∠ADF,
∵∠CDE+∠EDF+∠BDF=180°,
∴2(∠ADE+∠ADF)+∠BDF=180°,
2(∠ADE+90°﹣∠BDF)+∠BDF=180°,
∴∠BDF=2∠ADE;
(2)解:∵,∠BAC=90°,
∴,
∵AD⊥BC,
∴BD=CD=AD=4,
∵DG=3AG,DG+AG=AD,
∴AG=1,DG=3,
在EC上截取EN=EG,连接DN,过点N作NP⊥CD于P,如图1,
∵将△CDE沿DE折叠至△FDE,
∴∠DEG=∠DEN,
∵EN=EG,DE=DE,
∴△DEG≌△DEN(SAS),
∴DN=DG=3,
∵AB=AC,∠BAC=90°,
∴∠C=45°,
∵NP⊥CD,
∴∠CNP=∠C=45°,
∴NP=PC,
设NP=PC=x,由DP=4﹣x,,
在Rt△DPN中,由勾股定理,得x2+(4﹣x)2=32,
解得:,
∴,
∴,
∴当时,
△AGE的周长=.
当时,
△AGE的周长=.
综上,△AGE的周长为或;
(3)解:y的值是变化的;理由如下:
作∠BDF的平分线DN交AB于N,如图2,
∵DN平分∠BDF,
∴∠BDN=∠MDN,
由(1)知:∠BDF=2∠ADE,
∴∠BDN=∠MDN=∠ADE,
∵AB=AC,∠BAC=90°,AD⊥BC,
∴∠B=∠DAE=45°,BD=CD=AD,
∴△BDN≌△ADE(ASA),
∴AE=BN,DN=DE,∠BND=∠AED,
∵将△CDE沿DE折叠至△FDE,
∴∠CED=∠DEG,DF=CD,∠F=∠C=45°,
∵∠BND+∠DNM=∠AED+∠CED=180°,
∴∠DNM=∠DEG,
在△DMN与△DGE中,
,
∴△DMN≌△DGE(ASA),
∴DM=DG,MN=GE,
∵DF=CD,BD=CD=AD,
∴DF﹣DM=AD﹣DG,即FM=AG,
∵∠F=∠BAD=45°,∠MHF=∠GHA,FM=AG,
∴△FMH≌△AGH(AAS),
∴FH=AH,
,
∵AG=AD﹣DG,DG=DM,
∴,
∴y随着DM的增大而减小,
∵E在AC边上运动(不与点A重合),AE<CE,
∴点M在线段AB上,
∴DM<BD,即DM<4,
此时,
当DM⊥AB时,此时DM最小,
∵∠B=45°,
∴∠BDM=∠B=45°,
∴DM=BM,
∴由勾股定理,得2DM2=BD2=42,
∴,
此时y取得最大值为,即y≤8,
∴.
故y的值是变化的,变化范围为.
24.【答案】(1)﹣4;(2)x=时,最小值为8;(3)2.
【解答】解:(1)∵,
又,
∴y有最大值=2﹣6=﹣4;
(2)∵,
又,
当4(x﹣1)=时,即x=时,y有最小值=4+4=8;
(3)∵,
∵a,b,c是非负实数,
∴,
∴,
∴的最小值为2,
∴的最小值为2.
25.【答案】(1)14;
(2).
【解答】解:(1)由a、b是方程x2﹣4x+1=0的两个根,
可得a+b=4,ab=1,
;
(2)进行变形可得a+b=2﹣c,ab=c2﹣c,
∴a,b是x2﹣(2﹣c)x+c2﹣c=0的解,
根据根的判别式可得Δ=(2﹣c)2﹣4(c2﹣c)≥0,
整理得,
解得﹣≤c
∴正数c的最大值为.
26.【答案】见试题解答内容
【解答】解:∵∠C=∠ABC=2∠A,
∴∠C+∠ABC+∠A=5∠A=180°,
∴∠A=36°.
则∠C=∠ABC=2∠A=72°.
又BD是AC边上的高,
则∠DBC=90°﹣∠C=18°.
27.【答案】(1)证明见解答过程;
(2)60°.
【解答】(1)证明:∵△ABC和△CDE均为等边三角形,
∴AC=BC,∠ACB=∠ABC=∠CAB=60°,CD=CE,∠DCE=60°,
∴∠ACE=∠BCD,
在△ACE和△BCD中,
,
∴△ACE≌△BCD(SAS);
(2)解:∵∠ABC=60°,∠ABC+∠CBD=180°,
∴∠CBD=120°,
∵△ACE≌△BCD,
∴∠CAE=∠CBD=120°,
∴∠DAE=∠CAE﹣∠CAB=60°.
28.【答案】(1)见解析,A1(2,4),B1(4,1),C1(1,2);
(2)见解析,(﹣3,0).
【解答】解:(1)如图,△A1B1C1即为所作,A1(2,4),B1(4,1),C1(1,2);
(2)作出点C关于x轴的对称轴点C2,连接BC2交x轴于点P,即点P即为所作,点P的坐标为(﹣3,0).
29.【答案】110°.
【解答】解:∵在△ABC中,∠BAC=80°,∠B=60°,
∴∠ACB=180°﹣∠CAB﹣∠B=180°﹣80°﹣60°=40°,
又∵CF是∠ACB的平分线,
∴,
又∵AD是BC边上的高,
∴∠ADC=90°,
∴∠AEC=90°+∠ECD=90°+20°=110°.
30.【答案】证明见解答过程.
【解答】解:∵AF=CD,
∴AF+CF=CD+CF,即AC=DF,
又∵BC∥EF,
∴∠ACB=∠DFE,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(SAS),
∴BC=EF.
31.【答案】见试题解答内容
【解答】解:(1)设y=kx+b,
将(15,700)、(25,500)代入上式,得,
,
解得,
∴y=﹣20x+1000(10≤x≤30);
(2)依题意有:(x﹣10)(﹣20x+1000)=6000,
解得:x1=20,x2=40,
∵10≤x≤30,
∴x=20;
答:该书的销售单价20元;
(3)销售该书每天的利润不能达到9000元.理由如下:
根据题意得:(x﹣10)(﹣20x+1000)=9000,
整理得x2﹣60x+950=0,
∵Δ=602﹣4×1×950=﹣200<0,
∴该方程没有实数根,
∴销售该书每天的利润不能达到9000元.
32.【答案】(1)甲种水果购进110千克,则乙种水果购进50千克;
(2)安排购买甲种水果40kg,乙种水果120千克,才能使水果店在销售完这批水果时获利最多,此时利润为600元.
【解答】解:(1)设甲种水果购进x千克,则乙种水果购进(160﹣x)千克,
由题意可得:5x+9(160﹣x)=1000,
解得x=110,
∴160﹣x=50,
答:甲种水果购进110千克,则乙种水果购进50千克;
(2)设购进甲种水果m千克,则乙种水果购进(160﹣m)千克,获得的利润为w元,
由题意可得:w=(8﹣5)m+(13﹣9)(160﹣m)=﹣m+640,
∴w随m的增大而减小,
∵该水果店决定乙种水果的进货量不超过甲种水果的进货量的3倍,
∴160﹣m≤3m,
解得m≥40,
∴当m=40时,w取得最大值,此时w=600,160﹣m=120,
答:安排购买甲种水果40kg,乙种水果120千克,才能使水果店在销售完这批水果时获利最多,此时利润为600元.
33.【答案】见试题解答内容
【解答】(1)解:∵一次函数y1=ax+b经过点(1,0)和点(2,3),
∴a+b=0,2a+b=3,解得:a=3,b=﹣3,
∴y1的表达式为:y1=3x﹣3;
(2)①证明:∵一次函数y1=ax+b(a≠0)恒过定点(1,0),
∴a+b=0,
∴b=﹣a,
∴y1的表达式为:y1=ax﹣a,
∵y2=bx+a,
∴y2=﹣ax+a,
∵点A(m,p)在一次函数y1=ax﹣a的图象上,
∴p=ma﹣a,
∵点B(n,p)在一次函数y2=﹣ax+a的图象上,
∴p=﹣na+a,
∴ma﹣a=﹣na+a,
即ma+na=2a,
∵a≠0,
∴m+n=2;
②解:由①得y1=ax﹣a,y2=﹣ax+a,
∵y=y1﹣y2,
∴y=(ax﹣a)﹣(﹣ax+a)=2ax﹣2a,
∵a≠0,
∴有以下两种情况:
(ⅰ)当a<0时,
对于y=2ax﹣2a,y随x的增大而减小,
又∵﹣2≤x≤4,
∴当x=﹣2时,y为最大,
∴2a×(﹣2)﹣2a=6,
解得:a=﹣1
(ⅱ)当a>0时,
对于y=2ax﹣2a,y随x的增大而增大,
又∵﹣2≤x≤4,
∴当x=4时,y为最大,
∴2a×4﹣2a=6,
解得:a=1,
综上所述:当﹣2≤x≤4时,函数y有最大值6,a的值为﹣1或1.
34.【答案】见试题解答内容
【解答】解:任务一:由表格可知,每隔0.5小时,电池电量的增加量为25%;
任务二:由表格可知两个函数均为一次函数,设y1=k1t+b1,y2=k2s+b2,
对于y1=k1t+b1,当t=1时,y=50,当t=2时,y=100,
∴,解得:,
∴y1=50t;
对于y2=k2s+b2,当s=0时,y=100,当s=100时,y=50,
∴,解得:,
∴;
任务三:∵,
∴当s=40×3=120时,;
∵到达目的地,还需要250﹣120=130(千米),
∴还需消耗电量,
∴至少需充电65﹣40=25,
∴当y1=25时,50t=25,
∴t=0.5,
即:要保证司机在最短的时间快速到达目的地,则至少要在服务区充电0.5小时.
35.【答案】(1)(2)见解答.
【解答】解:(1)如图所示,△A′B′C即为所求;
(2)如图所示,点P即为所求.
36.【答案】(1)见解析;
(2)36°.
【解答】(1)证明:连接DE,
∵AD是BC边上的高线,
∴∠ADB=90°,
∵DE是AB边上的中线,
∴BE=,
∵AE=CD,
∴DE=CD,
∵点G为CE的中点,
∴DG⊥CE.
(2)解:连接DE,
则DE=AE=CD,
∵点G为CE的中点,
∴DG⊥CE,
∵BE=DE,EF=AF,
∴∠B=∠BDE,
设∠B=∠BDE=x,则∠AED=2x,∠AEF=y,
∴∠DEF=2x﹣y,
∵DE=DC,
∴∠DEF=∠BDE=x,
∴2x﹣y=x,
∴y=x,
∴x+x=90°,
∴x=36°,
∴∠B=36°.
37.【答案】(1)见解析;
(2)5.
【解答】(1)证明:∵四边形ABCD是菱形,
∴AB∥CD,AB=CD,
∵AF=CE,
∴FB=ED,
∴四边形DFBE是平行四边形,
∵BE⊥CD,
∴∠BED=90°,
∴四边形DFBE是矩形;
(2)解:在Rt△BDE中,DE===2,
∵四边形ABCD是菱形,
∴BC=CD,
∴CE=CD﹣DE=BC﹣2,
在Rt△BDE中,BC2=CE2+BE2,
∴BC2=(BC﹣2)2+42,
解得BC=5.
38.【答案】见试题解答内容
【解答】解:(1)当定价为200元时,(200﹣180)÷10=2(间).
(50﹣2)×(200﹣20)=8640(元).
故答案为:2;8640;
(2)设房价定为x元,
根据题意,得(x﹣20)(50﹣)=10890.
整理,得x2﹣700x+122500=0,
解得 x1=x2=350.
答:应该将每间房每天定价为350元.
39.【答案】114°.
【解答】解:∵BD平分∠ABC,∠ABC=48°,
∴,
∵AE⊥BC,
∴∠BEF=90°,
∴∠AFB=∠BEF+∠CBD=90°+24°=114°.
40.【答案】(1)证明见解答;(2)AD=BE+DE,理由见解答.
【解答】(1)证明:∵∠ACB=90°,
∴∠ACD+∠BCE=90°,
∵BE⊥MN,
∴∠CBE+∠BCE=90°,
∴∠ACD=∠CBE,
在△ADC和△CEB中,
,
∴△ADC≌△CEB(AAS);
(2)解:AD=BE+DE,
理由如下:∵△ADC≌△CEB,
∴AD=CE,BE=CD,
∴AD=CE=CD+DE=BE+DE.
41.【答案】x≤3.
【解答】解:解不等式x+3(x﹣2)≤6,得:x≤3,
解不等式x﹣1,得:x<4,
则不等式组的解集为x≤3.
42.【答案】2≤x<4,数轴见解析过程.
【解答】解:,
解不等式①得,x≥2,
解不等式②得,x<4,
∴不等式组的解集为2≤x<4,
不等式组的解集在数轴上表示为:
.
43.【答案】见试题解答内容
【解答】解:(1)由题意可得,
点B的横坐标为:1+=,纵坐标为:15,
∴点B的坐标为(,15),
故答案为:(,15);
(2)甲从点P跑到点N的速度为:=7.5千米/时,
故答案为:7.5;
(3)由题意可得,点D的坐标为(0.5,0),点C的坐标为(2,20),
设线段CD的函数函数表达式为y=kx+b,
,得,
即线段CD的表达式是y=x﹣(0.5≤x≤2).
44.【答案】(1)∠FCB=70°,∠F=45°;
(2)①见详解;
②.
【解答】(1)解:连接AE,BE,如图1所示:
∵点A关于直线BP的对称点E,
∴∠EBP=∠ABP=25°,AB=EB,
∵四边形ABCD是正方形,
∴AB=BC,∠ABC=90°,
∴∠EBC=90°﹣25°﹣25°=40°,
则,
∴∠F=180°﹣∠FBC﹣∠FCB=180°﹣(90°﹣25°)﹣70°=45°;
(2)①证明:连接AE,PE,如图2所示:
设∠ABP=a,∠APB=90°﹣a,
∵点A关于直线BP的对称点E,
∴AE⊥BP,AP=PE,∠PAE=∠PEA=a,∠DPE=2a,
∵P是AD中点,
∴AP=DP=PE,
则,
∵∠FPD=∠APB=90°﹣a,
∴∠ADE=∠FPD,
∴DE∥BF;
②解:如图3:连接AE,PE,点H,C关于AD对称,
∵CE的延长线交BP延长线于点F,连结DE,且P是AD中点,四边形ABCD是正方形,
∴HD=CD=AB,∠HDP=∠BAP=90°,HC∥AB,
∴∠DHP=∠ABP,
∴△HDP≌△BAP(AAS),
∴∠HPD=∠BPA,
则H,F,P三点共线,
∵DE∥BF,HD=CD,
∴DE∥HB,
∴DE是△CHF的中位线,
∴HF=2DE,CE=EF,
∵AB=6,
∴,
根据等面积法,得,
即,
设∠ABP=a,∠APB=90°﹣a,
由(1)知,BE=CB,BA=BE,
∴,
则∠FEO=180°﹣(90°﹣a)﹣(45°+a)=45°,
∵EA⊥BF,
∴∠EFO=45°,
则FO=EO,
∴,
∴.
45.【答案】见试题解答内容
【解答】解:(1)由折叠可得,∠ACE=∠DCE=∠ACD,∠BCF=∠B'CF=∠BCB',
又∵∠ACB=90°,
∴∠ACD+∠BCB'=90°,
∴∠ECD+∠FCD=×90°=45°,
即∠ECF=45°;
(2)由折叠可得,∠DEC=∠AEC=90°,BF=B'F=1,
∴∠EFC=45°=∠ECF,
∴CE=EF=4,
∴BE=4+1=5,
∴Rt△BCE中,BC==,
设AE=x,则AB=x+5,
∵Rt△ACE中,AC2=AE2+CE2,
Rt△ABC中,AC2=AB2﹣BC2,
∴AE2+CE2=AB2﹣BC2,
即x2+42=(x+5)2﹣41,
解得x=,
∴S△ABC=AB×CE=(+5)×4=.
46.【答案】(1)10,15,200.
(2)750米.
(3)17.5或20分钟.
【解答】解:(1)由题意得a=1500÷150=10,
b=10+5=15,
m=(3000﹣1500)÷(22.5﹣15)=200(米/分),
故答案为:10,15,200.
(2)设BC所在直线解析式为y=kx+b,
将(15,1500),(22.5,3000)代入y=kx+b得:
,
解得,
∴y=200x﹣1500(15≤x≤22.5),
∵小军速度为120米/分,
∴OD所在直线解析式为y=120x,
联立方程,
解得,
3000﹣2250=750(米),
∴小军在途中与爸爸第二次相遇时,距离图书馆750米.
(3)由题意得当x<时,120x﹣(200x﹣1500)=100,
解得x==17.5,
当x>时,200x﹣1500﹣120x=100,
解得x=20.
∴爸爸自第二次出发至到达图书馆前,小军骑行时间为17.5或20分钟时,两人相距100米.
47.【答案】(1)y=2x+6;
(2)点(﹣1,5)不在这个函数图象上.
【解答】解:(1)设这个函数的解析式为y=kx+b,
将点A(1,8)和点B(﹣3,0)代入可得:
,解得;
∴这个函数的解析式为y=2x+6;
(2)点(﹣1,5)不在这个函数图象上,理由如下:
将x=﹣1代入y=2x+6得:
y=2×(﹣1)+6=4≠5;
∴点(﹣1,5)不在这个函数图象上.
48.【答案】(1)55°;
(2)见解析.
【解答】(1)解:∵∠BAC=80°,∠C=70°,
∴∠ABC=180°﹣∠BAC﹣∠C=180°﹣80°﹣70°=30°,
∵AE,BF分别是∠BAC和∠ABC平分线,
∴∠BAE=BAC=40°,∠ABF=ABC=15°,
∴∠BOE=∠ABF+∠BAE=40°+15°=55°;
(2)证明:∵∠AEC=∠ABC+∠BAE=30°+40°=70°,
∴∠AEC=∠C,
∴AE=AC,
∵AD⊥CE,
∴DE=DC.
49.【答案】(1)见解析;
(2)见解析.
【解答】解:(1)如图所示,△ABC、△ABC1、△ABC2即为所求作;
(2)如图所示,△ABD即为所求,
50.【答案】任务1:描点并作图见解答;是,y=﹣2x+120(0≤x≤60),25;
任务2:h=﹣x+180(0≤x≤60);
任务3:cm.
【解答】解:任务1:描点并作图如图所示:
根据图象可知,变量x、y满足一次函数关系.
设y=kx+b(k、b为常数,且k≠0),
将x=2,y=116和x=10,y=100代入y=kx+b,
得,解得,
∴y=﹣2x+120.
将x=a和y=70代入y=﹣2x+120,
得﹣2a+120=70,解得a=25;
当背带都为单层部分时,x=0;
当背带都为双层部分时,y=0,即﹣2x+120=0,解得x=60,
∴x的取值范围是0≤x≤60.
任务2:∵背带的总长度为单层部分与双层部分的长度和,
∴总长度为﹣2x+120+x=﹣x+120,
当单肩包背带长度调整为最佳背带总长度时,得=,
∴h=﹣x+180(0≤x≤60).
任务3:由素材可知,当背包的背带调节到最短时都为双层部分,即x=60,y=0.
∵背包提在手上,且背包的悬挂点距地面高度为53.5cm,
∴手到地面的距离为(+53.5)cm,即83.5cm.
设小明爸爸的身高为h cm.
∵臂展和身高一样,且肩宽为38cm,
∴小明爸爸一条胳膊的长度为cm,
∴h++83.5=h,解得h=172,
根据任务2,得172=﹣x+180,解得x=,
∴此时双层部分的长度为cm.
声明:试题解
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
专题03 解答题
一.解答题(共50小题)
1.(2023秋 瓯海区校级期末)如图,△ABC是边长为6cm的等边三角形,点P,Q分别从顶点A,B同时出发,点P沿射线AB运动,点Q沿折线BC﹣CA运动,且它们的速度都为1cm/s.当点Q到达点A时,点P随之停止运动.连接PQ,PC,设点P的运动时间为t(s).
(1)当点Q在线段BC上运动时,BQ的长为 (cm),BP的长为 (cm)(用含t的式子表示);
(2)当PQ与△ABC的一条边垂直时,求t的值;
(3)在点Q从点C运动到点A的过程中,连接PQ,直接写出PQ中点O经过的路径长.
2.(2023秋 长兴县期末)如图,在△ABC中,AB=AC,过BC的中点D作DE⊥AB,DF⊥AC,垂足分别为点E、F.
(1)求证:DE=DF;
(2)若∠BDE=55°,求∠BAC的度数.
3.(2023秋 江北区期末)如图,两个形状,大小完全相同的含有30°,60°的三角板如图①放置,PA,PB与直线MN重合,且三角板PAC与三角板PBD均可绕点P逆时针旋转.
(1)试说明:∠DPC=90°;
(2)如图②,若三角板PAC的边PA从PN处开始绕点P逆时针旋转一定度数,PF平分∠APD,PE平分∠CPD,求∠EPF.
(3)如图③,若三角板PAC的边PA从PN处开始绕点P逆时针旋转,转速为3°/s.同时三角板PBD的边PB从PM处开始绕点P逆时针旋转,转速为2°/s,在两个三角板旋转过程中(PC转到与PM重合时,三角板都停止转动),问的值是否变化?若不变,求出其值,若变化,说明理由.
4.(2023秋 吴兴区期末)
背景 亚运会期间,小明所在的班级开展知识竞赛,需要去商店购买A、B两种款式的亚运盲盒作为奖品.
素材1 某商店在无促销活动时,若买15个A款亚运盲盒、10个B款亚运盲盒,共需230元;若买25个A款亚运盲盒、25个B款亚运盲盒,共需450元.
素材2 该商店龙年迎新春促销活动:用35元购买会员卡成为会员后,凭会员卡购买商店内任何商品,一律按商品价格的8折出售(已知小明在此之前不是该商店的会员);线上淘宝店促销活动:购买商店内任何商品,一律按商品价格的9折出售且包邮.
问题解决
任务1 某商店在无促销活动时,求A款亚运盲盒和B款亚运盲盒的销售单价各是多少元?
任务2 小明计划在促销期间购买A、B两款盲盒共40个,其中A款盲盒m个(0<m<40),若在线下商店购买,共需要 元;若在线上淘宝店购买,共需要 元.(均用含m的代数式表示)
任务3 请你帮小明算一算,在任务2的条件下,购买A款盲盒的数量在什么范围内时,线下购买方式更合算?
5.(2023秋 浦江县期末)如图,在四边形ABCD中,∠B=∠D=90°,点E,F分别在AB,AD上,AE=AF,CE=CF,求证:CB=CD.
6.(2023秋 吴兴区期末)如图,在△ABC中,E是AB上一点,AC与DE相交于点F,F是AC的中点,AB∥CD.
(1)求证:△AEF≌△CDF;
(2)若AB=10,CD=7,求BE的长.
7.(2023秋 北仑区期末)根据以下素材,探索完成任务.
如何确定拍照打卡板
素材一 设计师小聪为某商场设计拍照打卡板(如图1),图2为其平面设计图.该打卡板是轴对称图形,由长方形DEFG和等腰三角形ABC组成,且点B,F,G,C四点共线.其中,点A到BC的距离为1.2米,FG=0.8米,DG=1.5米.
素材二 因考虑牢固耐用,小聪打算选用甲、乙两种材料分别制作长方形DEFG与等腰三角形ABC(两种图形无缝隙拼接),且甲材料的单价为85元/平方米,乙材料的单价为100元/平方米.
问题解决
任务一 推理最大高度 小聪说:“如果我设计的方案中CB长与C,D两点间的距离相等,那么最高点B到地面的距离就是线段DG长”,他的说法对吗?请判断并说明理由.
任务二 探究等腰三角形ABC面积 假设CG长度为x米,等腰三角形ABC的面积为S.求S关于x的函数表达式.
任务三 确定拍照打卡板 小聪发现他设计的方案中,制作拍照打卡板的总费用不超过180元,请你确定CG长度的最大值.
8.(2023秋 滨江区期末)如图,在△ABC中,∠ABC=45°,CD⊥AB于点D,BE⊥AC于点E,CD与BE相交于点F.
(1)求证:BF=AC;
(2)若∠A=60°,△ADC的中线DG=1,求BC的长.
9.(2023秋 莲都区期末)已知一次函数y=kx+b的图象经过点A(﹣1,3)和点B(1,﹣1).
(1)求此一次函数的表达式;
(2)若点C(a,2)向右平移3个单位后恰好落在直线AB上,求a的值.
10.(2023秋 莲都区期末)如图,∠A=∠D,∠B=∠E,AF=CD.
(1)求证:△ABC≌△DEF;
(2)若∠A=20°,∠E=75°,求∠BCF的度数.
11.(2023秋 滨江区期末)如图,为了测量一条两岸平行的河流宽度,由于跨河测量困难,所以,三个数学研究小组设计了不同的方案,他们在河南岸的点B处,测得河北岸的一棵树底部A点恰好在点B的正北方向,测量方案如下表:
课题 测量河流宽度
工具 测量角度的仪器(仪器的高度忽略不计),标杆,皮尺等
小组 第一小组 第二小组 第三小组
测量方案 观测者从B点向正东走到C点,此时恰好测得:∠ACB=45° 观测者从B点向正东走到E点,O是BE的中点,继续从点E沿垂直于BE的EF方向走,直到点A,O,F在一条直线上.
测量示意图
(1)第一小组认为,河宽AB的长度就是线段 的长度.
(2)第二小组方案灵感来源于古希腊哲学家泰勒斯,他们认为只要测得EF的长就是所求河宽AB的长,你认为第二小组的方案可行吗?如果可行,请给出证明;如果不可行,请说明理由.
(3)请你代表第三小组,设计一个测量方案,把测量方案和测量示意图填入上表,然后指明你画的示意图中,只要测出哪条线段的长,就能推算出河宽AB长,并说明方案的可行性.
12.(2023秋 莲都区期末)如图,直线m的函数表达式为y=﹣2x﹣6,与x轴交于点A,直线n经过点B(2,0)和点C(0,﹣1),且直线m,n交于点D.
(1)求点A,点D的坐标.
(2)点P是x轴上的一个动点,求PA+PB+PC+PD的最小值.
(3)点M,N分别是直线m,n上的两点,且不与点A,B重合.当△MND≌△BAD时,直接写出每一组点M和点N的坐标.
13.(2023秋 长兴县期末)如图,在△ABC中,AB=AC,过CA的延长线上一点D,作DE⊥BC,垂足为E,交边AB于点F.
(1)求证:△ADF是等腰三角形;
(2)若AD=13,BE=5,F为AB的中点,求EF的长.
14.(2023秋 鄞州区期末)在平面直角坐标系中,O为原点,点A(0,3),B(﹣4,0),C(4,0).若将点B向右平移10个单位长度,再向上平移4个单位长度,得到对应点D.
(1)点D的坐标为 ;
(2)若点P是y轴上一动点,若△PAC的面积等于△CAD的面积,请求出点P的坐标;
(3)若点E为x轴上一动点,若△EAC为等腰三角形,请直接写出点E的坐标.
15.(2023秋 余姚市期末)如图,在△ABC中,AB=AC=5,BC=6,点D在AC边上,BD=AB.(1)求△ABC的面积;
(2)求AD的长.
16.(2023秋 鄞州区期末)【基础练习】
(1)如图1,在等腰Rt△ABC中,∠C=90°,AC=1,AD平分∠BAC交BC于点D,DE⊥AB于点E,求BE的长.
【类比探究】
(2)如图2,AD是△ABC的角平分线,∠B=40°,∠C=80°,点E在AB上,AE=AC.求证:AB=AC+CD.
【拓展延伸】
(3)如图3,点P是等边△ABC外一点,连结PA,PC,PB,恰好满足PA=AB.AD平分∠PAB交PC于点D,线段AD,CD,PD之间有什么关系?请作出猜测并进行证明.
17.(2023秋 北仑区期末)如图,已知AB=AD,∠BAD=∠CAE,∠B=∠D,AD与BC交于点P,点C在DE上.
(1)求证:AC=AE;
(2)若∠B=36°,∠APC=72°.
①求∠E的度数;
②求证:CP=CE.
18.(2023秋 瓯海区校级期末)如图,点A、C、D、B在同一条直线上,点E、F分别在直线AB的两侧,AE=BF,CE=DF,AD=BC.
(1)求证:△ACE≌△BDF.
(2)若∠CDF=55°,求∠ACE的度数.
19.(2023秋 海曙区校级期末)如图,点B、C、D在同一条直线上,AB⊥BD,DE⊥BD,AC⊥CE,AB=CD.
(1)求证:△ABC≌△CDE.
(2)若∠ACB=37°,求∠AED的度数.
20.(2023秋 东阳市期末)我们新定义一种三角形:若一个三角形中存在两边的平方差等于第三边上高的平方,则称这个三角形为勾股高三角形,两边交点为勾股顶点.
●特例感知
①等腰直角三角形 勾股高三角形(请填写“是”或者“不是”);
②如图1,已知△ABC为勾股高三角形,其中C为勾股顶点,CD是AB边上的高.若BD=2AD=2,试求线段CD的长度.
●深入探究
如图2,已知△ABC为勾股高三角形,其中C为勾股顶点且CA>CB,CD是AB边上的高.试探究线段AD与CB的数量关系,并给予证明;
●推广应用
如图3,等腰△ABC为勾股高三角形,其中AB=AC>BC,CD为AB边上的高,过点D向BC边引平行线与AC边交于点E.若CE=a,试求线段DE的长度.
(2023秋 鄞州区期末)解方程:.
22.(2023秋 鄞州区期末)如图,在两个完全相同的甲、乙容器中,最初,容器甲有10cm高的水,容器乙放了一个长方体,且容器底面积是长方体底面积的4倍.从甲容器向乙容器用虹吸原理注水(虹吸装置的体积忽略不计),当注满时,容器乙中液面与长方体上底面相平.设容器甲中的液面高为y1(单位:cm),容器乙中的液面高为y2(单位:cm).小科绘制了y1、y2关于时间x(单位:s)的函数图象如图2所示.回答下列问题:
(1)a的值为 ;容器甲的液面下降速度是 cm/s:
(2)求b的值以及y2关于x的函数表达式;
(3)当容器甲中的液面高y1与容器乙中的液面高y2相差2cm时,求此时x的值.
23.(2023秋 鄞州区期末)如图,在△ABC中,,∠BAC=90°,AD⊥BC,E在AC边上运动(不与点A重合),AE<CE,将△CDE沿DE折叠至△FDE,EF分别与AD,AB交于G,H两点.
(1)求证:∠BDF=2∠ADE;
(2)如图1,若DG=3AG,求△AGE的周长;
(3)如图2,设DF与AB交于点M,在整个运动过程中,记△FMH与△AEG的周长之和为y,则y的值是否变化,若变化求出范围;若不变,求出y.
24.(2023秋 鄞州区期末)【阅读材料】小明在兴趣小组学习了“基本不等式”的相关知识.整理如下:对于正数a、b,有,所以a+b﹣2≥0,即a+b≥2(当且仅当a=b时取到等号)特别地,a+=2(当且仅当a=1时取到等号),因此,当a>0时,a+有最小值2,此时a=1.
【简单应用】小明完成了大部分老师布置的作业,但还有两题不会,请你帮一帮他.
(1)函数y=2﹣x﹣(x>0)的最大值为 .
(2)求函数y=4x+(x>1)的最小值,并写出取最小值时x的值.
【猜想提升】小明由上述的a+b≥2提出猜想:a+b+c≥3(当且仅当a=b=c时取到等号).通过查阅资料,他惊奇地发现这个猜想是正确的,请你利用小明这个猜想解答下面的问题.
设a,b,c是非负实数,求的最小值.
25.(2023秋 鄞州区期末)(1)已知a、b是方程x2﹣4x+1=0的两个根,求的值.
(2)已知a、b、c均为实数,且a+b+c=2,ab+c=c2,求正数c的最大值.
26.(2022秋 拱墅区校级期末)如图,在△ABC中,∠C=∠ABC=2∠A,BD是AC边上的高,求∠DBC的度数.
27.(2023秋 慈溪市期末)如图,已知△ABC和△CDE均为等边三角形,点D在AB的延长线上,连结AE.
(1)求证:△ACE≌△BCD;
(2)求∠DAE的度数.
28.(2023秋 台州期末)如图,在平面直角坐标系中,A(﹣2,4),B(﹣4,1),C(﹣1,2).
(1)在图中画出△ABC关于y轴的对称图形△A1B1C1,并写出点A1,B1,C1的坐标;
(2)请在x轴上画出点P的位置,使得PB+PC最短,并直接写出点P的坐标.
29.(2023秋 台州期末)如图,在△ABC中,∠BAC=80°,∠B=60°,AD是BC边上的高,∠ACB的平分线CF交AD于点E.求∠AEC的度数.
30.(2023秋 台州期末)如图,点A,F,C,D在同一条直线上,AF=CD,∠A=∠D,BC∥EF.求证:BC=EF.
31.(2023秋 镇海区校级期末)近年来,电商平台直播带货成了一个火热的新兴职业,某主播带货图书《苏东坡传》,他用双语直播,风趣幽默,点燃了不同年龄者的读书热情.已知这本书的成本价为10元,规定销售单价不低于成本价,且不高于成本价的3倍,通过前几天的销售发现,该书每天的销售量y(本)与销售单价x(元/本)之间近似满足一次函数关系,部分对应数据如表:
x(元/本) … 15 25 …
y(本) … 700 500 …
(1)根据表格提供的数据,求y关于x的函数关系式,并写出x的取值范围.
(2)若销售该书每天的利润为6000元,求该书的销售单价.
(3)销售该书每天的利润能否达到9000元?请说明理由.
32.(2023秋 鄞州区期末)为迎接新春佳节的到来,一水果店计划购进甲、乙两种新出产的水果共160千克,这两种水果的进价、售价如表所示:
进价(元/千克) 售价(元/千克)
甲种 5 8
乙种 9 13
(1)若该水果店预计进货款为1000元,则这两种水果各购进多少千克?
(2)若该水果店决定乙种水果的进货量不超过甲种水果的进货量的3倍,应怎样安排进货才能使水果店在销售完这批水果时获利最多?此时利润为多少元?
33.(2023秋 上城区期末)一次函数y1=ax+b(a≠0)恒过定点(1,0).
(1)若一次函数y1=ax+b还经过(2,3)点,求y1的表达式;
(2)若有另一个一次函数y2=bx+a.
①点A(m,p)和点B(n,p)分别在一次函数y1和y2的图象上,求证:m+n=2;
②设函数y=y1﹣y2,当﹣2≤x≤4时,函数y有最大值6,求a的值.
34.(2023秋 南浔区期末)【问题背景】新能源汽车多数采用电能作为动力来源,不需要燃烧汽油,这样就减少了二氧化碳等气体的排放,从而达到保护环境的目的.
【实验操作】
为了解汽车电池需要多久能充满,以及充满电量状态下汽车的最大行驶里程,某综合实践小组设计两组实验,实验一:探究电池充电状态下汽车仪表盘显示电量y1(%)与时间t(小时)的关系,数据记录如表1.
实验二:探究充满电量状态下汽车行驶过程中仪表盘显示电量y2(%)与行驶里程s(千米)的关系,数据记录如表2.
电池充电状态
时间t(小时) 0.5 1 1.5 2
电量y1(%) 25 50 75 100
表1
汽车行驶过程
已行驶里程s(千米) 0 80 100 140
电量y2(%) 100 60 50 30
表2
任务一:计算表1中每隔0.5小时电池电量的增加量;
【建立模型】
任务二:请结合表1、表2的数据,选择合适的数学模型,求出y1关于t的函数表达式及y2关于s的函数表达式;
【解决问题】
任务三:某电动汽车在充满电量的状态下出发,前往距离出发点250千米处的目的地,若电动车平均每小时行驶40千米,行驶3小时后,在途中的服务区充电,一次性充电若干时间后汽车以原速度继续行驶,若要保证司机在最短的时间快速到达目的地,则至少要在服务区充电多长时间?
35.(2023秋 台州期末)如图,在正方形网格中,点A,B,C均为网格线交点,请按要求作图,作图过程仅使用无刻度的直尺,保留作图痕迹,无需说明理由.
(1)如图1,作出△ABC关于直线MN对称的图形;
(2)如图2,在直线MN上求作点P,使得∠APM=∠BPN.
36.(2023秋 西湖区期末)如图,在△ABC中,AD是BC边上的高线,CE是AB边上的中线,AD与CE交于点F,点G为CE的中点,CD=AE.
(1)求证:DG⊥CE.
(2)若AF=EF,求∠B的度数.
37.(2023秋 江北区期末)在菱形ABCD中,过点B作BE⊥CD于点E,点F在边AB上,AF=CE,连接BD、DF.
(1)求证:四边形BFDE是矩形;
(2)若BD=2,BE=4,求BC的长.
38.(2023秋 江北区期末)宾馆有50间房供游客居住,当每间房每天定价为180元时宾馆会住满;当每间房每天的定价加10元时,就会空一间房,如果有游客居住,宾馆还需对居住的每间房每天支出20元的费用.
(1)当定价为200元时,会空 间房,每天的利润是 元.
(2)若宾馆每天想获得的利润为10890元,应该将每间房每天定价为多少元?
39.(2023秋 路桥区期末)如图,在△ABC中,BD平分∠ABC,AE⊥BC于点E,交BD于点F.若∠ABC=48°,求∠AFB的度数.
40.(2023秋 江北区期末)如图,∠ACB=90°,AC=BC,AD⊥MN,BE⊥MN,垂足分别是D,E.
(1)求证:△ADC≌△CEB;
(2)猜想线段AD,BE,DE之间具有怎样的数量关系,并说明理由.
(2023秋 余姚市期末)解一元一次不等式组:.
42.(2023秋 舟山期末)解不等式组,并将解集在数轴上表示出来.
43.(2023秋 江北区期末)现有一段20千米长,可供长跑爱好者跑步的笔直跑道MN,已知甲、乙两人都从M点出发,甲跑到途中的P点后原地休息了20分钟,之后继续跑到N点,共用时间2小时;乙虽然比甲晚出发半小时,但和甲同时到达N点.假设两人跑步时均为匀速,在甲出发后的2小时内两人离开M点的距离y(千米)与时间x(小时)的函数关系如图所示.请回答下列问题:
(1)图中B点的坐标为
(2)甲从点P跑到点N的速度为 千米/时;
(3)求图中线段CD的表达式.并写出定义域.
44.(2023秋 江北区期末)如图,在正方形ABCD中,若P是AD上一点,点A关于直线BP的对称点E,连结CE,且CE的延长线交BP延长线于点F,连结DE.
(1)若∠ABP=25°,求∠FCB和∠F的度数.
(2)若P是AD中点;
①求证:DE∥BF;
②若AB=6时,直接写出CF的长.
45.(2023秋 宁波期末)如图,在△ABC中,∠ACB=90°,点E,F在边AB上,将边AC沿CE翻折,使点A落在AB上的点D处,再将边BC沿CF翻折,使点B落在CD的延长线上的点B'处.
(1)求∠ECF的度数;
(2)若CE=4,B'F=1,求线段BC的长和△ABC的面积.
46.(2023秋 鄞州区校级期末)“低碳环保,绿色出行”的理念得到广大群众的接受,越来越多的人喜欢选择自行车作为出行工具.小军和爸爸同时从家骑自行车去图书馆,爸爸先以150米/分的速度骑行一段时间,休息了5分钟,再以m米/分的速度到达图书馆,小军始终以同一速度骑行,两人行驶的路程y(米)与时间x(分钟)的关系如图,请结合图象,解答下列问题:
(1)a= ,b= ,m= ;
(2)若小军的速度是120米/分,求小军在途中与爸爸第二次相遇时,距图书馆的距离;
(3)在(2)的条件下,爸爸自第二次出发后至到达图书馆前,何时与小军相距100米,请求出此时小军骑行的时间.(直接写出答案)
47.(2023秋 瓯海区校级期末)已知一次函数的图象经过点A(1,8)和点B(﹣3,0),
(1)求这个一次函数的解析式;
(2)判断点(﹣1,5)在不在该图象上,并说明理由.
48.(2023秋 东阳市期末)在△ABC中,AD是高,AE,BF是角平分线,AE交BF于点O,∠BAC=80°,∠C=70°.
(1)求∠BOE的大小;
(2)求证:DE=DC.
49.(2023秋 瓯海区校级期末)如图1,图2都是4×4的正方形网格,每个小正方形的顶点称为格点.如图,线段AB的两端点均在格点上,在给定的网格中,按下列要求用无刻度的直尺画等腰△ABC,使点C在格点上.
(1)在图1中,画以AB为腰的三角形;
(2)在图2中,画以AB为底的三角形.
50.(2023秋 上城区期末)综合与实践
生活中的数学:如何确定单肩包最佳背带长度
素材1 如图是一款单肩包,背带由双层部分、单层部分和调节扣构成.使用时可以通过调节扣加长或缩短单层部分的长度,使背带的总长度加长或缩短(总长度为单层部分与双层部分的长度和,其中调节扣的长度忽略不计).
素材2 对于该背包的背带长度进行测量,设双层的部分长度是x cm,单层部分的长度是y cm,得到如下数据:双层部分长度x(cm)261014a单层部分长度y(cm)1161081009270
素材3 单肩包的最佳背带总长度与身高比例为2:3
素材4 小明爸爸准备购买此款背包.爸爸自然站立,将该背包的背带调节到最短提在手上,背带在背包的悬挂点离地面的高度为53.5cm;已知爸爸的臂展和身高一样,且肩宽为38cm,头顶到肩膀的垂直高度为总身高的.
任务1 在平面直角坐标系中,以所测得数据中的x为横坐标,以y为纵坐标,描出所表示的点,并用光滑曲线连接,根据图象思考变量x、y是否满足一次函数关系.如果是,求出该函数的表达式,直接写出a值并确定x的取值范围.
任务2 设人身高为h,当单肩包背带长度调整为最佳背带总长度时,求此时人身高h与这款背包的背带双层部分的长度x之间的函数表达式.
任务3 当小明爸爸的单肩包背带长度调整为最佳背带总长度时.求此时双层部分的长度.
参考答案与试题解析
一.解答题(共50小题)
1.【答案】(1)t,6﹣t;
(2)满足条件的t的值为2或4或8.
(3)3cm.
【解答】解:(1)由题意BQ=t cm,PB=(6﹣t)cm.
故答案为:t,6﹣t;
(2)如图1中,当PQ⊥BC时,
∵∠PQB=90°,∠B=60°,
∴∠BPQ=30°,
∴PB=2BQ,
∴6﹣t=2t,
∴t=2.
如图2中,当QP⊥AB时,同法可得QB=2PB,
∴t=2(6﹣t),
∴t=4.
如图3中,当PQ⊥AC时,同法可得AP=2AQ,
∴t=2(12﹣t),
∴t=8,
综上所述,满足条件的t的值为2或4或8.
(3)如图,过Q作QH∥BC交AB于H,
则△AHQ是等边三角形,
∴AQ=AH,
∵AC=AB,
∴CQ=BH,
∵CQ=BP,
∴BH=BP,
∴QE=PE,
∴点E是PQ的中点,
∴在点Q从点C运动到点A的过程中,连接PQ,PQ中点O经过的路径长为BC=3(cm).
2.【答案】(1)证明见解答;(2)∠BAC=110°.
【解答】(1)证明:连接AD,
∵D是BC的中点,AB=AC,
∴AD平分∠BAC,
∵DE⊥AB,DF⊥AC,
∴DE=DF;
(2)解:∵DE⊥AB,
∴∠BED=90°,
∵∠BDE=55°,
∴∠B=35°,
∴∠C=35°,
∴∠BAC=110°.
3.【答案】见试题解答内容
【解答】解:(1)∵∠DPC=180°﹣∠CPA﹣∠DPB,∠CPA=60°,∠DPB=30°,
∴∠DPC=180°﹣30°﹣60°=90°;
(2)设∠CPE=∠DPE=x,∠CPF=y,
则∠APF=∠DPF=2x+y,
∵∠CPA=60°,
∴y+2x+y=60°,
∴x+y=30°
∴∠EPF=x+y=30°
(3)不变.
设运动时间为t秒,则∠BPM=2t,
∴∠BPN=180﹣2t,∠APN=3t.
∴∠CPD=360﹣∠DPB﹣∠BPN﹣∠CPA﹣∠APN=90﹣t,
∴==.
4.【答案】(任务1)该商店在无促销活动时,A款亚运盲盒的销售单价是10元,B款亚运盲盒的销售单价是8元;
(任务2)(1.6m+291),(1.8m+288);
(任务3)当购买A款盲盒的数量超过15个且少于40个时,线下购买方式更合算.
【解答】解:(任务1)设该商店在无促销活动时,A款亚运盲盒的销售单价是x元,B款亚运盲盒的销售单价是y元,
根据题意得:,
解得:.
答:该商店在无促销活动时,A款亚运盲盒的销售单价是10元,B款亚运盲盒的销售单价是8元;
(任务2)根据题意得:在线下商店购买,共需要35+10×0.8m+8×0.8(40﹣m)=(1.6m+291)(元);
在线上淘宝店购买,共需要10×0.9m+8×0.9(40﹣m)=(1.8m+288)(元).
故答案为:(1.6m+291),(1.8m+288);
(任务3)根据题意得:1.6m+291<1.8m+288,
解得:m>15,
又∵0<m<40,
∴15<m<40.
答:当购买A款盲盒的数量超过15个且少于40个时,线下购买方式更合算.
5.【答案】见试题解答内容
【解答】证明:如图,连接AC,
在△ACE和△ACF中,
,
∴△ACE≌△ACF(SSS),
∴∠EAC=∠FAC,
∵∠B=∠D=90°,
∴CB=CD.
6.【答案】(1)证明见解答;
(2)3.
【解答】(1)证明:∵AB∥CD,
∴∠A=∠DCF,
∵点F是AC的中点,
∴AF=CF,
在△AEF和△CDF中,
,
∴△AEF≌△CDF(ASA),
(2)解:由(1)得:△AEF≌△CDF,
∴AE=CD,
∵AB=10,CD=7,
∴BE=AB﹣AE=AB﹣CD=10﹣7=3.
7.【答案】见试题解答内容
【解答】解:任务1:他的说法对,理由如下:
如图:过点B作BH⊥DC于点H,
∴∠BHC=90°.
∵四边形EFGD是长方形,
∴∠DGC=90°.
∴∠BHC=∠DGC,
在△BCH与△DCG中,
,
∴△BCH≌△DCG(AAS),
∴BH=DG.
∴最高点B到地面的距离就是线段DG长.
任务2:∵该指示牌是轴对称图形,四边形EFHD是长方形,
∴设BF=CG=x,则BC=2x+0.8.
又△ABC的高为1.2米,
∴三角形ABC的面积S=×(2x+0.8)×1.2=1.2x+0.48.
任务3:由题意,当长方形用甲种材料制作,三角形用乙种材料制作时,
又长方形的面积为:DH DE=0.8×1.5=1.2(平方米),
∴1.2×85+(1.2x+0.48)×100≤180.
解得x≤0.25,
故CG长度的最大值为0.25米.
8.【答案】(1)证明见解答过程;
(2).
【解答】(1)证明:∵CD⊥AB,
∴∠CDA=∠BDF=90°,
∴∠DBF+∠DFB=180°﹣∠BDF=90°,
又∵BE⊥AC,
∴∠BEA=90°,
∴∠DBF+∠DAC=180°﹣∠BEA=90°,
∴∠DAC=∠DFB,
又∵∠ABC=45°,
∴∠DCB=180°﹣∠ABC﹣∠BDF=45°=∠ABC,
∴BD=CD,
在△ACD和△FBD中,
,
∴△ACD≌△FBD(AAS),
∴AC=BF;
(2)解:如图,
在Rt△ACD中,中线DG=1,
∴AC=2DG=2,
∵∠A=60°,∠ADC=90°,
∴∠ACD=30°,
∴AD=AC=1,
∴CD===BD,
∴BC==.
9.【答案】(1)y=﹣2x+1;
(2).
【解答】解:(1)将点A(﹣1,3)和点B(1,﹣1)代入y=kx+b,
得,
解得:k=﹣2,b=1,
∴一次函数的表达式为y=﹣2x+1;
(2)点C(a,2)向右平移3个单位后坐标为(a+3,2),
∵点(a+3,2)在直线AB上,
∴2=﹣2(a+3)+1,
解得:.
10.【答案】(1)证明见解析;
(2)95°.
【解答】(1)证明:∵AF=CD,
∴AF﹣CF=CD﹣CF,
即AC=DF,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(AAS);
(2)解:∵∠B=∠E,∠E=75°
∴∠B=75°,
∵∠BCF是△ABC的一个外角,
∴∠BCF=∠A+∠B,
∵∠A=20°,
∴∠BCF=20°+75°=95°.
11.【答案】见试题解答内容
【解答】解:(1)∵AB⊥BC,∠ACB=45°,
∴△ABC是等腰直角三角形,
∴BC=AB,
∴河宽AB的长度就是线段BC的长度.
故答案为:BC;
(2)第二小组的方案可行,理由如下:
∵O是BE中点,
∴OB=OE,
∵AB⊥BE,EF⊥BE,
∴∠ABO=∠FEO=90°,
在△ABO和△FEO中,
,
∴△ABO≌△FEO(ASA),
∴EF=AB,
∴河宽AB的长度就是线段EF的长度.
(3)见表格,
课题 测量河流宽度
工具 测量角度的仪器(仪器的高度忽略不计),标杆,皮尺等
小组 第一小组 第二小组 第三小组
测量方案 观测者从B点向正东走到C点,此时恰好测得:∠ACB=45° 观测者从B点向正东走到E点,O是BE的中点,继续从点E沿垂直于BE的EF方向走,直到点A,O,F在一条直线上. 观测者从B点向正西走到C点,使用测量角度的仪器测得∠BCD=∠ACB=65°,CD交AB延长线于D,
测量示意图
只要测出BD的长,就能推算出河宽AB长,理由如下:
∵AB⊥BC,
∴∠ABC=∠DBC=90°,
在△ABC和△DBC中,
,
∴△ABC≌△DBC(ASA),
∴BD=AB,
∴河宽AB的长等于线段BD的长.
12.【答案】见试题解答内容
【解答】解:(1)∵直线m的函数表达式为y=﹣2x﹣6,与x轴交于点A,
令y=0,可得0=﹣2x﹣6,解得x=﹣3,
∴A(﹣3,0),
设直线n的解析式为y=kx+b,
∵直线n经过点B(2,0)和点C(0,﹣1),
∴,解得,
∴直线n的解析式为y=x﹣1,
联立y=﹣2x﹣6得,解得,
∴点D的坐标为(﹣2,﹣2);
(2)作点C关于x轴的对称点E,连接DE交x轴于点P,连接CP,
∴PE=PC,E(0,1),
∴PC+PD=PD+PE,此时PC+PD=DE最小,PA+PB=AB最小,
∵点D的坐标为(﹣2,﹣2),A(﹣3,0),B(2,0),
∴DE==,AB=2+3=5,
∴PA+PB+PC+PD的最小值为5+;
(3)∵点D的坐标为(﹣2,﹣2),A(﹣3,0),点D的坐标为(﹣2,﹣2);
∴AB=2+3=5,AD==,BD==2,
设M(m,﹣2m﹣6),N(n,n﹣1),
当△MND≌△BAD时,ND=AD=,MD=BD=2,
∴=2,=,
解得m=0或﹣4,n=0或﹣4,
∴点M和点N的坐标分别为(﹣4,2)、(0,﹣1)或(0,﹣6)、(0,﹣1)或(﹣4,2)、(﹣4,﹣3)或(0,﹣6)、(﹣4,﹣3).
13.【答案】见试题解答内容
【解答】解:(1)证明:∵在△ABC中,AB=AC,
∴∠B=∠C,
∵DE⊥BC,
∴∠B+∠BFE=90°,∠C+∠D=90°,
∴∠BFE=∠D,
又∵∠BFE=∠AFD,
∴∠D=∠AFD,
∴△ADF 是等腰三角形;
(2)∵F为AB的中点,
∴AF=BF,
∵△ADF是等腰三角形,
BF=AF=AD=13,
∵DE⊥BC,
∴EF==12,
答:EF的长为12.
14.【答案】(1)(6,4);
(2)(0,)或(0,﹣);
(3)(,0)或(﹣4,0)或(﹣1,0)或(9,0).
【解答】解:(1)∵B(﹣4,0),将点B向右平移10个单位长度,再向上平移4个单位长度,得到对应点D.
∴D的坐标为(﹣4+10,0+4)即D的坐标为:(6,4);
故答案为:(6,4);
(2)设点P(0,a),
△CAD的面积为4×6﹣×3×6﹣×2×4﹣×4×3=11,
△PAC的面积为×|a﹣3|×4=2|a﹣3|,
∵△PAC的面积等于△CAD的面积,
∴2|a﹣3|=11,
解得a=或﹣,
∴P的坐标为(0,)或(0,﹣);
(3)△EAC为等腰三角形,当AC为底时,点E在AC的垂直平分线上,如图:
∴AE=CE,
设OE=x,CE=AE=4﹣x,
在Rt△AOE中,32+x2=(4﹣x)2,
解得x=,
∴E的坐标为(,0);
当AC为腰时,如图,
若AE=AC=5,此时E的坐标为(﹣4,0),
若AC=AE=5,此时OE=1,E的坐标为(﹣1,0),
若AC=AE=5,此时E的坐标为(9,0),
综上所述,若△EAC为等腰三角形,点E的坐标为(,0)或(﹣4,0)或(﹣1,0)或(9,0).
15.【答案】(1)12;
(2).
【解答】解:(1)过点A作AM⊥BC于点M,
∵AB=AC,AM⊥BC,
∴M是BC的中点,
∵AB=5,BC=6,
∴BM=CM=3,
∴AM===4,
∴△ABC的面积=BC AM=×6×4=12;
(2)解法一:过点B作BN⊥AC于点N,
∵BD=AB,
∴AN=DN=AD,
∵△ABC的面积=AC BN=×5 BN=12;
∴BN=,
AN==,
∴AD=2AN=.
解法二:过点B作BN⊥AC于点N,
∵BD=AB,
∴AN=DN=AD,
设AN=x,则CN=5﹣x,
∵AB=AC,AM⊥BC,
∵BN2=AB2﹣AN2=BC2﹣CN2,
∴25﹣x2=36﹣(5﹣x)2,
∴x=,
∴AD=2AN=.
16.【答案】(1)﹣1;
(2)证明见解析;
(3)AD+PD=CD,证明见解析.
【解答】(1)解:∵△ABC是等腰直角三角形,∠C=90°,AC=1,
∴AB=AC=,
∵AD平分∠BAC,DE⊥AB,
∴DE=DC,
在Rt△ADE和Rt△ADC中,
,
∴Rt△ADE≌Rt△ADC(HL),
∴AE=AC=1,
∴BE=AC﹣AE=﹣1;
(2)证明:∵AD为△ABC的角平分线,
∴∠CAD=∠EAD,
在△AED和△ACD中,
,
∴△AED≌△ACD(SAS),
∴∠AED=∠C=80°,ED=CD,
∵∠AED=∠B+∠EDB,
∴∠EDB=∠AED﹣∠B=80°﹣40°=40°,
∴∠B=∠EDB,
∴ED=EB,
∴EB=CD,
∵AB=AE+EB,
∴AB=AC+CD;
(3)解:AD+PD=CD,证明如下:
如图3,在CD上取点E,使CE=PD,连接AE,
∵△ABC是等边三角形,
∴AB=AC,∠BAC=60°,
∵PA=AB,
∴AC=PA,
∴∠APD=∠ACE,
在△APD和△ACE中,
,
∴△APD≌△ACE(SAS),
∴AD=AE,∠PAD=∠CAE,
∵AD平分∠PAB,
∴∠PAD=∠BAD,
∴∠BAD=∠CAE,
∴∠BAD+∠BAE=∠CAE+∠BAE,
即∠DAE=∠BAC=60°,
∴△ADE是等边三角形,
∴AD=DE,
∵DE+CE=CD,
∴AD+PD=CD.
17.【答案】(1)证明见解答过程;
(2)①72°;
②证明见解答过程.
【解答】(1)证明:∵∠BAD=∠CAE,
∴∠BAD+∠DAC=∠CAE+∠DAC,
即∠BAC=∠DAE,
在△BAC和△DAE中,
,
∴△BAC≌△DAE(ASA),
∴AC=AE;
(2)①解:∵∠B=36°,∠APC=72°,
∴∠BAP=∠APC﹣∠B=72°﹣36°=36°,
∴∠CAE=36°,
∵△BAC≌△DAE,
∴AC=AE,
∴∠ACE=∠E=×(180°﹣∠CAE)=×(180°﹣36°)=72°;
②证明:∵△BAC≌△DAE,
∴∠ACB=∠E,
∴∠ACB=∠ACE,∠APC=∠E,
在△ACP和△ACE中,
,
∴△ACP≌△ACE(AAS),
∴CP=CE.
18.【答案】见试题解答内容
【解答】(1)证明:∵AD=BC,
∴AD﹣CD=BC﹣CD,
∴AC=BD;
在△ACE和△BDF中,
,
∴△ACE≌△BDF(SSS);
(2)解:由(1)可知:△ACE≌△BDF,
∴∠ACE=∠BDF,
∵∠CDF=55°,
∴∠BDF=125°=∠ACE.
19.【答案】(1)见解析过程;
(2)82.
【解答】(1)证明:∵AB⊥BD,DE⊥BD,AC⊥CE,
∴∠B=∠D=∠ACE=90°.
∴∠BAC+∠ACB=90°,∠ACB+∠DCE=90°.
∴∠BAC=∠DCE.
在△ABC和△CDE中,
,
∴△ABC≌△CDE(ASA).
(2)解:∵△ABC≌△CDE,
∴AC=CE,∠ACB=∠CED=37°,
∴∠CAE=∠AEC=45°,
∴∠AED=37°+45°=82°.
20.【答案】见试题解答内容
【解答】解:●特例感知:
① 等腰直角三角形是勾股高三角形.
故答案为:是.
②如图1中,根据勾股定理可得:CB2=CD2+4,CA2=CD2+1,
于是CD2=(CD2+4)﹣(CD2+1)=3,
∴CD=.
●深入探究:
如图2中,由CA2﹣CB2=CD2可得:CA2﹣CD2=CB2,而CA2﹣CD2=AD2,
∴AD2=CB2,
即AD=CB;
●推广应用:
过点A向ED引垂线,垂足为G,
∵“勾股高三角形”△ABC为等腰三角形,且AB=AC>BC,
∴只能是AC2﹣BC2=CD2,由上问可知AD=BC……①.
又ED∥BC,∴∠1=∠B……②.
而∠AGD=∠CDB=90°……③,
∴△AGD≌△CDB(AAS),
∴DG=BD.
易知△ADE与△ABC均为等腰三角形,
根据三线合一原理可知ED=2DG=2BD.
又AB=AC,AD=AE,
∴BD=EC=a,
∴ED=2a.
21.【答案】.
【解答】解:,
两边平方得,
整理可得,
两边平方得,
整理得,
令,
可得4t=(t+1)2,
解得t=1,
∴,
整理得x2﹣x﹣1=0
解得,
根据二次根式有意义的条件可得x≥1,
∴.
22.【答案】(1)10;1;
(2);;
(3)或.
【解答】解:(1)根据题意可得容器甲有10cm高的水,
故a=10,
根据图象可得容器甲的水10s放完,故容器甲的液面下降速度是(cm/s),
故答案为:10;1;
(2)根据图像可得b为容器甲放完水时,容器乙中水面高度,
设长方体底面积为t cm2,则容器底面积为4t cm2,
∴水的体积为4t 10=40t cm3,
容器乙实际可装水的底面积为4t﹣t=3t cm2,
∴容器乙中水面高度为,即,
设y2=kx,把代入,得:
,
解得,
∴;
(3)设y1=kx+b,把(0,10),(10,0)代入函数解析式得:
,
解得,
∴y1=﹣x+10,
①当y1﹣y2=2时,可得,
解得;
②当y2﹣y1=2时,可得,
解得x=,
∴当容器甲中的液面高y1与容器乙中的液面高y2相差2cm时,此时x的值为或.
23.【答案】(1)见解析;
(2)或;
(3)y的值是变化的,变化范围为.
【解答】(1)证明:∵AD⊥BC,
∴∠BDF+∠ADF=∠ADB=90°,
∴∠ADF=90°﹣∠BDF,
∵将△CDE沿DE折叠至△FDE,
∴∠CDE=∠EDF=∠ADE+∠ADF,
∵∠CDE+∠EDF+∠BDF=180°,
∴2(∠ADE+∠ADF)+∠BDF=180°,
2(∠ADE+90°﹣∠BDF)+∠BDF=180°,
∴∠BDF=2∠ADE;
(2)解:∵,∠BAC=90°,
∴,
∵AD⊥BC,
∴BD=CD=AD=4,
∵DG=3AG,DG+AG=AD,
∴AG=1,DG=3,
在EC上截取EN=EG,连接DN,过点N作NP⊥CD于P,如图1,
∵将△CDE沿DE折叠至△FDE,
∴∠DEG=∠DEN,
∵EN=EG,DE=DE,
∴△DEG≌△DEN(SAS),
∴DN=DG=3,
∵AB=AC,∠BAC=90°,
∴∠C=45°,
∵NP⊥CD,
∴∠CNP=∠C=45°,
∴NP=PC,
设NP=PC=x,由DP=4﹣x,,
在Rt△DPN中,由勾股定理,得x2+(4﹣x)2=32,
解得:,
∴,
∴,
∴当时,
△AGE的周长=.
当时,
△AGE的周长=.
综上,△AGE的周长为或;
(3)解:y的值是变化的;理由如下:
作∠BDF的平分线DN交AB于N,如图2,
∵DN平分∠BDF,
∴∠BDN=∠MDN,
由(1)知:∠BDF=2∠ADE,
∴∠BDN=∠MDN=∠ADE,
∵AB=AC,∠BAC=90°,AD⊥BC,
∴∠B=∠DAE=45°,BD=CD=AD,
∴△BDN≌△ADE(ASA),
∴AE=BN,DN=DE,∠BND=∠AED,
∵将△CDE沿DE折叠至△FDE,
∴∠CED=∠DEG,DF=CD,∠F=∠C=45°,
∵∠BND+∠DNM=∠AED+∠CED=180°,
∴∠DNM=∠DEG,
在△DMN与△DGE中,
,
∴△DMN≌△DGE(ASA),
∴DM=DG,MN=GE,
∵DF=CD,BD=CD=AD,
∴DF﹣DM=AD﹣DG,即FM=AG,
∵∠F=∠BAD=45°,∠MHF=∠GHA,FM=AG,
∴△FMH≌△AGH(AAS),
∴FH=AH,
,
∵AG=AD﹣DG,DG=DM,
∴,
∴y随着DM的增大而减小,
∵E在AC边上运动(不与点A重合),AE<CE,
∴点M在线段AB上,
∴DM<BD,即DM<4,
此时,
当DM⊥AB时,此时DM最小,
∵∠B=45°,
∴∠BDM=∠B=45°,
∴DM=BM,
∴由勾股定理,得2DM2=BD2=42,
∴,
此时y取得最大值为,即y≤8,
∴.
故y的值是变化的,变化范围为.
24.【答案】(1)﹣4;(2)x=时,最小值为8;(3)2.
【解答】解:(1)∵,
又,
∴y有最大值=2﹣6=﹣4;
(2)∵,
又,
当4(x﹣1)=时,即x=时,y有最小值=4+4=8;
(3)∵,
∵a,b,c是非负实数,
∴,
∴,
∴的最小值为2,
∴的最小值为2.
25.【答案】(1)14;
(2).
【解答】解:(1)由a、b是方程x2﹣4x+1=0的两个根,
可得a+b=4,ab=1,
;
(2)进行变形可得a+b=2﹣c,ab=c2﹣c,
∴a,b是x2﹣(2﹣c)x+c2﹣c=0的解,
根据根的判别式可得Δ=(2﹣c)2﹣4(c2﹣c)≥0,
整理得,
解得﹣≤c
∴正数c的最大值为.
26.【答案】见试题解答内容
【解答】解:∵∠C=∠ABC=2∠A,
∴∠C+∠ABC+∠A=5∠A=180°,
∴∠A=36°.
则∠C=∠ABC=2∠A=72°.
又BD是AC边上的高,
则∠DBC=90°﹣∠C=18°.
27.【答案】(1)证明见解答过程;
(2)60°.
【解答】(1)证明:∵△ABC和△CDE均为等边三角形,
∴AC=BC,∠ACB=∠ABC=∠CAB=60°,CD=CE,∠DCE=60°,
∴∠ACE=∠BCD,
在△ACE和△BCD中,
,
∴△ACE≌△BCD(SAS);
(2)解:∵∠ABC=60°,∠ABC+∠CBD=180°,
∴∠CBD=120°,
∵△ACE≌△BCD,
∴∠CAE=∠CBD=120°,
∴∠DAE=∠CAE﹣∠CAB=60°.
28.【答案】(1)见解析,A1(2,4),B1(4,1),C1(1,2);
(2)见解析,(﹣3,0).
【解答】解:(1)如图,△A1B1C1即为所作,A1(2,4),B1(4,1),C1(1,2);
(2)作出点C关于x轴的对称轴点C2,连接BC2交x轴于点P,即点P即为所作,点P的坐标为(﹣3,0).
29.【答案】110°.
【解答】解:∵在△ABC中,∠BAC=80°,∠B=60°,
∴∠ACB=180°﹣∠CAB﹣∠B=180°﹣80°﹣60°=40°,
又∵CF是∠ACB的平分线,
∴,
又∵AD是BC边上的高,
∴∠ADC=90°,
∴∠AEC=90°+∠ECD=90°+20°=110°.
30.【答案】证明见解答过程.
【解答】解:∵AF=CD,
∴AF+CF=CD+CF,即AC=DF,
又∵BC∥EF,
∴∠ACB=∠DFE,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(SAS),
∴BC=EF.
31.【答案】见试题解答内容
【解答】解:(1)设y=kx+b,
将(15,700)、(25,500)代入上式,得,
,
解得,
∴y=﹣20x+1000(10≤x≤30);
(2)依题意有:(x﹣10)(﹣20x+1000)=6000,
解得:x1=20,x2=40,
∵10≤x≤30,
∴x=20;
答:该书的销售单价20元;
(3)销售该书每天的利润不能达到9000元.理由如下:
根据题意得:(x﹣10)(﹣20x+1000)=9000,
整理得x2﹣60x+950=0,
∵Δ=602﹣4×1×950=﹣200<0,
∴该方程没有实数根,
∴销售该书每天的利润不能达到9000元.
32.【答案】(1)甲种水果购进110千克,则乙种水果购进50千克;
(2)安排购买甲种水果40kg,乙种水果120千克,才能使水果店在销售完这批水果时获利最多,此时利润为600元.
【解答】解:(1)设甲种水果购进x千克,则乙种水果购进(160﹣x)千克,
由题意可得:5x+9(160﹣x)=1000,
解得x=110,
∴160﹣x=50,
答:甲种水果购进110千克,则乙种水果购进50千克;
(2)设购进甲种水果m千克,则乙种水果购进(160﹣m)千克,获得的利润为w元,
由题意可得:w=(8﹣5)m+(13﹣9)(160﹣m)=﹣m+640,
∴w随m的增大而减小,
∵该水果店决定乙种水果的进货量不超过甲种水果的进货量的3倍,
∴160﹣m≤3m,
解得m≥40,
∴当m=40时,w取得最大值,此时w=600,160﹣m=120,
答:安排购买甲种水果40kg,乙种水果120千克,才能使水果店在销售完这批水果时获利最多,此时利润为600元.
33.【答案】见试题解答内容
【解答】(1)解:∵一次函数y1=ax+b经过点(1,0)和点(2,3),
∴a+b=0,2a+b=3,解得:a=3,b=﹣3,
∴y1的表达式为:y1=3x﹣3;
(2)①证明:∵一次函数y1=ax+b(a≠0)恒过定点(1,0),
∴a+b=0,
∴b=﹣a,
∴y1的表达式为:y1=ax﹣a,
∵y2=bx+a,
∴y2=﹣ax+a,
∵点A(m,p)在一次函数y1=ax﹣a的图象上,
∴p=ma﹣a,
∵点B(n,p)在一次函数y2=﹣ax+a的图象上,
∴p=﹣na+a,
∴ma﹣a=﹣na+a,
即ma+na=2a,
∵a≠0,
∴m+n=2;
②解:由①得y1=ax﹣a,y2=﹣ax+a,
∵y=y1﹣y2,
∴y=(ax﹣a)﹣(﹣ax+a)=2ax﹣2a,
∵a≠0,
∴有以下两种情况:
(ⅰ)当a<0时,
对于y=2ax﹣2a,y随x的增大而减小,
又∵﹣2≤x≤4,
∴当x=﹣2时,y为最大,
∴2a×(﹣2)﹣2a=6,
解得:a=﹣1
(ⅱ)当a>0时,
对于y=2ax﹣2a,y随x的增大而增大,
又∵﹣2≤x≤4,
∴当x=4时,y为最大,
∴2a×4﹣2a=6,
解得:a=1,
综上所述:当﹣2≤x≤4时,函数y有最大值6,a的值为﹣1或1.
34.【答案】见试题解答内容
【解答】解:任务一:由表格可知,每隔0.5小时,电池电量的增加量为25%;
任务二:由表格可知两个函数均为一次函数,设y1=k1t+b1,y2=k2s+b2,
对于y1=k1t+b1,当t=1时,y=50,当t=2时,y=100,
∴,解得:,
∴y1=50t;
对于y2=k2s+b2,当s=0时,y=100,当s=100时,y=50,
∴,解得:,
∴;
任务三:∵,
∴当s=40×3=120时,;
∵到达目的地,还需要250﹣120=130(千米),
∴还需消耗电量,
∴至少需充电65﹣40=25,
∴当y1=25时,50t=25,
∴t=0.5,
即:要保证司机在最短的时间快速到达目的地,则至少要在服务区充电0.5小时.
35.【答案】(1)(2)见解答.
【解答】解:(1)如图所示,△A′B′C即为所求;
(2)如图所示,点P即为所求.
36.【答案】(1)见解析;
(2)36°.
【解答】(1)证明:连接DE,
∵AD是BC边上的高线,
∴∠ADB=90°,
∵DE是AB边上的中线,
∴BE=,
∵AE=CD,
∴DE=CD,
∵点G为CE的中点,
∴DG⊥CE.
(2)解:连接DE,
则DE=AE=CD,
∵点G为CE的中点,
∴DG⊥CE,
∵BE=DE,EF=AF,
∴∠B=∠BDE,
设∠B=∠BDE=x,则∠AED=2x,∠AEF=y,
∴∠DEF=2x﹣y,
∵DE=DC,
∴∠DEF=∠BDE=x,
∴2x﹣y=x,
∴y=x,
∴x+x=90°,
∴x=36°,
∴∠B=36°.
37.【答案】(1)见解析;
(2)5.
【解答】(1)证明:∵四边形ABCD是菱形,
∴AB∥CD,AB=CD,
∵AF=CE,
∴FB=ED,
∴四边形DFBE是平行四边形,
∵BE⊥CD,
∴∠BED=90°,
∴四边形DFBE是矩形;
(2)解:在Rt△BDE中,DE===2,
∵四边形ABCD是菱形,
∴BC=CD,
∴CE=CD﹣DE=BC﹣2,
在Rt△BDE中,BC2=CE2+BE2,
∴BC2=(BC﹣2)2+42,
解得BC=5.
38.【答案】见试题解答内容
【解答】解:(1)当定价为200元时,(200﹣180)÷10=2(间).
(50﹣2)×(200﹣20)=8640(元).
故答案为:2;8640;
(2)设房价定为x元,
根据题意,得(x﹣20)(50﹣)=10890.
整理,得x2﹣700x+122500=0,
解得 x1=x2=350.
答:应该将每间房每天定价为350元.
39.【答案】114°.
【解答】解:∵BD平分∠ABC,∠ABC=48°,
∴,
∵AE⊥BC,
∴∠BEF=90°,
∴∠AFB=∠BEF+∠CBD=90°+24°=114°.
40.【答案】(1)证明见解答;(2)AD=BE+DE,理由见解答.
【解答】(1)证明:∵∠ACB=90°,
∴∠ACD+∠BCE=90°,
∵BE⊥MN,
∴∠CBE+∠BCE=90°,
∴∠ACD=∠CBE,
在△ADC和△CEB中,
,
∴△ADC≌△CEB(AAS);
(2)解:AD=BE+DE,
理由如下:∵△ADC≌△CEB,
∴AD=CE,BE=CD,
∴AD=CE=CD+DE=BE+DE.
41.【答案】x≤3.
【解答】解:解不等式x+3(x﹣2)≤6,得:x≤3,
解不等式x﹣1,得:x<4,
则不等式组的解集为x≤3.
42.【答案】2≤x<4,数轴见解析过程.
【解答】解:,
解不等式①得,x≥2,
解不等式②得,x<4,
∴不等式组的解集为2≤x<4,
不等式组的解集在数轴上表示为:
.
43.【答案】见试题解答内容
【解答】解:(1)由题意可得,
点B的横坐标为:1+=,纵坐标为:15,
∴点B的坐标为(,15),
故答案为:(,15);
(2)甲从点P跑到点N的速度为:=7.5千米/时,
故答案为:7.5;
(3)由题意可得,点D的坐标为(0.5,0),点C的坐标为(2,20),
设线段CD的函数函数表达式为y=kx+b,
,得,
即线段CD的表达式是y=x﹣(0.5≤x≤2).
44.【答案】(1)∠FCB=70°,∠F=45°;
(2)①见详解;
②.
【解答】(1)解:连接AE,BE,如图1所示:
∵点A关于直线BP的对称点E,
∴∠EBP=∠ABP=25°,AB=EB,
∵四边形ABCD是正方形,
∴AB=BC,∠ABC=90°,
∴∠EBC=90°﹣25°﹣25°=40°,
则,
∴∠F=180°﹣∠FBC﹣∠FCB=180°﹣(90°﹣25°)﹣70°=45°;
(2)①证明:连接AE,PE,如图2所示:
设∠ABP=a,∠APB=90°﹣a,
∵点A关于直线BP的对称点E,
∴AE⊥BP,AP=PE,∠PAE=∠PEA=a,∠DPE=2a,
∵P是AD中点,
∴AP=DP=PE,
则,
∵∠FPD=∠APB=90°﹣a,
∴∠ADE=∠FPD,
∴DE∥BF;
②解:如图3:连接AE,PE,点H,C关于AD对称,
∵CE的延长线交BP延长线于点F,连结DE,且P是AD中点,四边形ABCD是正方形,
∴HD=CD=AB,∠HDP=∠BAP=90°,HC∥AB,
∴∠DHP=∠ABP,
∴△HDP≌△BAP(AAS),
∴∠HPD=∠BPA,
则H,F,P三点共线,
∵DE∥BF,HD=CD,
∴DE∥HB,
∴DE是△CHF的中位线,
∴HF=2DE,CE=EF,
∵AB=6,
∴,
根据等面积法,得,
即,
设∠ABP=a,∠APB=90°﹣a,
由(1)知,BE=CB,BA=BE,
∴,
则∠FEO=180°﹣(90°﹣a)﹣(45°+a)=45°,
∵EA⊥BF,
∴∠EFO=45°,
则FO=EO,
∴,
∴.
45.【答案】见试题解答内容
【解答】解:(1)由折叠可得,∠ACE=∠DCE=∠ACD,∠BCF=∠B'CF=∠BCB',
又∵∠ACB=90°,
∴∠ACD+∠BCB'=90°,
∴∠ECD+∠FCD=×90°=45°,
即∠ECF=45°;
(2)由折叠可得,∠DEC=∠AEC=90°,BF=B'F=1,
∴∠EFC=45°=∠ECF,
∴CE=EF=4,
∴BE=4+1=5,
∴Rt△BCE中,BC==,
设AE=x,则AB=x+5,
∵Rt△ACE中,AC2=AE2+CE2,
Rt△ABC中,AC2=AB2﹣BC2,
∴AE2+CE2=AB2﹣BC2,
即x2+42=(x+5)2﹣41,
解得x=,
∴S△ABC=AB×CE=(+5)×4=.
46.【答案】(1)10,15,200.
(2)750米.
(3)17.5或20分钟.
【解答】解:(1)由题意得a=1500÷150=10,
b=10+5=15,
m=(3000﹣1500)÷(22.5﹣15)=200(米/分),
故答案为:10,15,200.
(2)设BC所在直线解析式为y=kx+b,
将(15,1500),(22.5,3000)代入y=kx+b得:
,
解得,
∴y=200x﹣1500(15≤x≤22.5),
∵小军速度为120米/分,
∴OD所在直线解析式为y=120x,
联立方程,
解得,
3000﹣2250=750(米),
∴小军在途中与爸爸第二次相遇时,距离图书馆750米.
(3)由题意得当x<时,120x﹣(200x﹣1500)=100,
解得x==17.5,
当x>时,200x﹣1500﹣120x=100,
解得x=20.
∴爸爸自第二次出发至到达图书馆前,小军骑行时间为17.5或20分钟时,两人相距100米.
47.【答案】(1)y=2x+6;
(2)点(﹣1,5)不在这个函数图象上.
【解答】解:(1)设这个函数的解析式为y=kx+b,
将点A(1,8)和点B(﹣3,0)代入可得:
,解得;
∴这个函数的解析式为y=2x+6;
(2)点(﹣1,5)不在这个函数图象上,理由如下:
将x=﹣1代入y=2x+6得:
y=2×(﹣1)+6=4≠5;
∴点(﹣1,5)不在这个函数图象上.
48.【答案】(1)55°;
(2)见解析.
【解答】(1)解:∵∠BAC=80°,∠C=70°,
∴∠ABC=180°﹣∠BAC﹣∠C=180°﹣80°﹣70°=30°,
∵AE,BF分别是∠BAC和∠ABC平分线,
∴∠BAE=BAC=40°,∠ABF=ABC=15°,
∴∠BOE=∠ABF+∠BAE=40°+15°=55°;
(2)证明:∵∠AEC=∠ABC+∠BAE=30°+40°=70°,
∴∠AEC=∠C,
∴AE=AC,
∵AD⊥CE,
∴DE=DC.
49.【答案】(1)见解析;
(2)见解析.
【解答】解:(1)如图所示,△ABC、△ABC1、△ABC2即为所求作;
(2)如图所示,△ABD即为所求,
50.【答案】任务1:描点并作图见解答;是,y=﹣2x+120(0≤x≤60),25;
任务2:h=﹣x+180(0≤x≤60);
任务3:cm.
【解答】解:任务1:描点并作图如图所示:
根据图象可知,变量x、y满足一次函数关系.
设y=kx+b(k、b为常数,且k≠0),
将x=2,y=116和x=10,y=100代入y=kx+b,
得,解得,
∴y=﹣2x+120.
将x=a和y=70代入y=﹣2x+120,
得﹣2a+120=70,解得a=25;
当背带都为单层部分时,x=0;
当背带都为双层部分时,y=0,即﹣2x+120=0,解得x=60,
∴x的取值范围是0≤x≤60.
任务2:∵背带的总长度为单层部分与双层部分的长度和,
∴总长度为﹣2x+120+x=﹣x+120,
当单肩包背带长度调整为最佳背带总长度时,得=,
∴h=﹣x+180(0≤x≤60).
任务3:由素材可知,当背包的背带调节到最短时都为双层部分,即x=60,y=0.
∵背包提在手上,且背包的悬挂点距地面高度为53.5cm,
∴手到地面的距离为(+53.5)cm,即83.5cm.
设小明爸爸的身高为h cm.
∵臂展和身高一样,且肩宽为38cm,
∴小明爸爸一条胳膊的长度为cm,
∴h++83.5=h,解得h=172,
根据任务2,得172=﹣x+180,解得x=,
∴此时双层部分的长度为cm.
声明:试题解
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
