上海市宝山区通河中学2024-2025学年高二上学期期中数学试卷(PDF版,含答案)
文档属性
| 名称 | 上海市宝山区通河中学2024-2025学年高二上学期期中数学试卷(PDF版,含答案) |

|
|
| 格式 | |||
| 文件大小 | 610.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-08 00:00:00 | ||
图片预览


文档简介
上海市宝山区通河中学 2024-2025 学年高二上学期期中数学试卷
一、单选题:本题共 4 小题,每小题 3 分,共 12 分。在每小题给出的选项中,只有一项是符合题目要求的。
1.在空间中,“两条直线没有公共点”是“这两条直线平行”的( )
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
2
2.已知圆锥侧面展开图的圆心角为 ,底面周长为2 .则这个圆锥的体积为( )
3
√ 2 2√ 2 4√ 2
A. B. √ 2 C. D.
3 3 3
1 1 1 1
3.化简式子 + + + + ,得( )
1×3 3×5 5×7 2023×2025
2022 2024 1011 1012
A. B. C. D.
2025 2025 2025 2025
4.已知 , 是空间中两条不同的直线,平面 , 是两个不同的平面,下列命题中正确的是( )
A. 若 // , ,则 //
B. 若 ⊥ , ⊥ ,则 //
C. 若 ⊥ , // , // ,则 ⊥
D. 若 // , // , , ,则 //
二、填空题:本题共 12 小题,共 42 分。
5.已知复数 = 3 4 ,| | = ______.
6.若向量 = ( 3,1), = (2, ),且 与 垂直,则实数 =______.
7.在数列{ }中, 1 = 2, +1 = 2( ∈ , ≥ 1),则 5 = ______.
3
8.设 = , ∈ ( , ),则 的值为 .
5 2
9.命题:若直线 与平面 上的无数条直线垂直,则 ⊥ ,是______命题(选填“真”或“假”).
10.向量 = (3,5)在向量 = (1,1)方向上的数量投影为______.
11.正方体 1 1 1 1中,二面角 1 1的大小为______.
12.数列{ }中,其前 项和 =
2 + 2 ,则 5 = ______.
1
13.已知无穷数列{ }满足 +1 = ( 为正整数),且
∞
2 = 1,记 为数列{ }的前 项和,则∑ =1 = 2
______.
14.给出以下四个命题:
①如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线和交线平行;
第 1 页,共 6 页
②如果一条直线和一个平面上的两条相交直线都垂直,那么这条直线垂直于这个平面;
③如果两条直线都平行于一个平面,那么这两条直线互相平行;
④ 、 与平面 成角相等,则 // .
其中是真命题的有______.
15.在数列{ }中, 1 = 6,且 = 1 + lg ( ≥ 2),则 100 = ______. 1
16.如图,在直四棱柱 1 1 1 1中,底面 为菱形,且∠ = 60°.
若 = 1 = 2,点 为棱 1的中点,点 在 1 上,则线段 , 的长度
和的最小值为______.
三、解答题:本题共 5 小题,共 60 分。解答应写出文字说明,证明过程或演算步骤。
17.(本小题12分)
已知函数 ( ) = .
(1)求 ( )的最小正周期;
(2)求 ( )在区间[ , ]上的最大值和最小值.
6 3
18.(本小题12分)
已知{ }是等差数列,{ }是等比数列,且 2 = 3, 3 = 9, 1 = 1, 14 = 4.
(1)求{ }的通项公式;
(2)设 = + ,求数列{ }的前 项和.
19.(本小题12分)
据《黑鞑事略》记载:“穹庐有二样:燕京之制,用柳木为骨,正如南方罘思,可以卷舒,面前开门,上
如伞骨,顶开一窍,谓之天窗,皆以毡为衣,马上可载.草地之制,以柳木组定成硬圈,径用毡挞定,不可
卷舒,车上载行.”随着畜牧业经济的发展和牧民生活的改善,穹庐或毡帐逐渐被蒙古包代替.一个普通的蒙
古包可视为一个圆锥与一个圆柱的组合体.如图,已知该圆锥的高为3米,圆柱的高为4米,底面直径为8米.
第 2 页,共 6 页
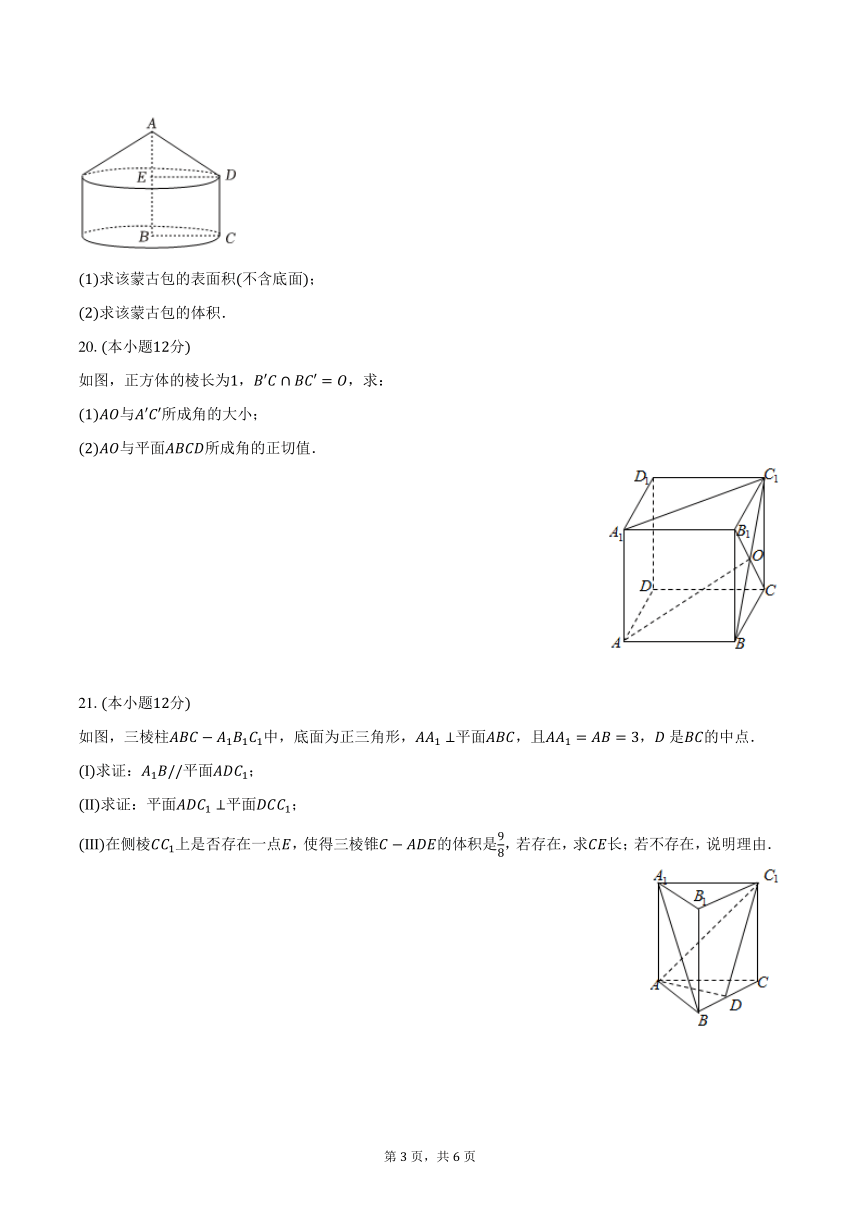
(1)求该蒙古包的表面积(不含底面);
(2)求该蒙古包的体积.
20.(本小题12分)
如图,正方体的棱长为1, ′ ∩ ′ = ,求:
(1) 与 ′ ′所成角的大小;
(2) 与平面 所成角的正切值.
21.(本小题12分)
如图,三棱柱 1 1 1中,底面为正三角形, 1 ⊥平面 ,且 1 = = 3, 是 的中点.
(Ⅰ)求证: 1 //平面 1;
(Ⅱ)求证:平面 1 ⊥平面 1;
9
(Ⅲ)在侧棱 1上是否存在一点 ,使得三棱锥 的体积是 ,若存在,求 长;若不存在,说明理由. 8
第 3 页,共 6 页
1.【答案】
2.【答案】
3.【答案】
4.【答案】
5.【答案】5
6.【答案】 6
7.【答案】6
3
8.【答案】
4
9.【答案】假
10.【答案】4√ 2
11.【答案】45°
12.【答案】11
13.【答案】4
14.【答案】①②
15.【答案】8
16.【答案】√ 9 + 2√ 10
1 2
17.【答案】解:(1) ( ) = 2 , = = ,则 ( )的最小正周期为 .
2 2
2 √ 3 √ 3 1 1
(2) ≤ ≤ ,则 ≤ 2 ≤ , ≤ 2 ≤ 1, ≤ 2 ≤ .
6 3 3 3 2 4 2 2
1 √ 3
所以 ( )在[ , ]上的最大值为 ,最小值为 .
6 3 2 4
18.【答案】解:(1)设{ }是公差为 的等差数列,{ }是公比为 的等比数列,
由 32 = 3, 3 = 9,可得 = = 3, 2
= · 2 = 3 · 3 2 2 = 3
1;
即有 1 = 1 = 1, 14 = 4 = 27,
则 = 14 1 = 2,
13
则 = 1 + ( 1) = 1 + 2( 1) = 2 1;
(2) = +
1
= 2 1 + 3 ,
第 4 页,共 6 页
则数列{ }的前 项和为:
[1 + 3 + + (2 1)] + (1 + 3 + 9 + + 3 1)
2 1 3
= · +
2 1 3
3 1
= 2 + .
2
19.【答案】解:(1) ∵蒙古包可视为一个圆锥与一个圆柱的组合体,
且该圆锥的高为3米,圆柱的高为4 ,底面直径为8 ,
∴ = √ 32 + 42 = 5,又 = 4,
1
故该蒙古包的表面积为 × 8 × 5 + 8 × 4 = 52 ( 2);
2
(2)由题意可得该蒙古包的体积为:
1 1
× 2 × + × 2 × = × 48 + 64 = 80 ( 3).
3 3
20.【答案】解:(1) ∵ ′ ′// ,
∴ 与 ′ ′所成的角就是∠ .
∵ ⊥平面 ′, 平面 ′,
∴ ⊥ ,
又 ⊥ , ∩ = , , 平面 ,
∴ ⊥平面 .
又 平面 ,∴ ⊥ ,
1
在 △ 中, √ 2 = , = √ 2,sin∠ = = ,
2 2
∴ ∠ = 30°.
即 与 ′ ′所成角为30°.
(2)如图,作 ⊥ 于 ,连接 .
∵平面 ′ ⊥平面 ,平面 ′ ∩平面 = , 平面 ′,
∴ ⊥平面 ,
∴ ∠ 为 与平面 所成的角.
1
在 △ 中, = , 1 √ 5
2 = √ 1
2 + ( )2 = ,
2 2
√ 5
∴ tan∠ = = .
5
即 与平面 所成角的正切值为√ 5.
5
第 5 页,共 6 页
(3)由(1)可知 ⊥平面 .
又∵ 平面 ,∴平面 ⊥平面 .
即平面 与平面 所成的角为90°.
21.【答案】解:(Ⅰ)连接 1 交 1于点 ,连接 .
∵三棱柱 1 1 1中, 1 ⊥平面 ,
∴四边形 1 1为矩形,可得点 为 1 的中点.
∵ 为 中点,得 为△ 1 中位线,
∴ 1 // .
∵ 平面 1, 1 平面 1,
∴ 1 //平面 1. … (4分)
(Ⅱ) ∵底面 正三角形, 是 的中点
∴ ⊥
∵ 1 ⊥平面 , 平面 ,∴ 1 ⊥ .
∵ 1 ∩ = ,∴ ⊥平面 1,
∵ 平面 1,∴平面 1 ⊥平面 1. … (9分)
9
(Ⅲ)假设在侧棱 1上存在一点 ,使三棱锥 的体积是 ,设 = 8
∵三棱锥 的体积 =
1 1 9
,得1 1 3 3√ 3 9∴ × × × × = × × × × = .
3 2 8 3 2 2 2 8
∴ = √ 3,即 = √ 3
9
∴在侧棱 1上存在一点 ,当 = √ 3时,三棱锥 的体积是 . … (14分) 8
第 6 页,共 6 页
一、单选题:本题共 4 小题,每小题 3 分,共 12 分。在每小题给出的选项中,只有一项是符合题目要求的。
1.在空间中,“两条直线没有公共点”是“这两条直线平行”的( )
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
2
2.已知圆锥侧面展开图的圆心角为 ,底面周长为2 .则这个圆锥的体积为( )
3
√ 2 2√ 2 4√ 2
A. B. √ 2 C. D.
3 3 3
1 1 1 1
3.化简式子 + + + + ,得( )
1×3 3×5 5×7 2023×2025
2022 2024 1011 1012
A. B. C. D.
2025 2025 2025 2025
4.已知 , 是空间中两条不同的直线,平面 , 是两个不同的平面,下列命题中正确的是( )
A. 若 // , ,则 //
B. 若 ⊥ , ⊥ ,则 //
C. 若 ⊥ , // , // ,则 ⊥
D. 若 // , // , , ,则 //
二、填空题:本题共 12 小题,共 42 分。
5.已知复数 = 3 4 ,| | = ______.
6.若向量 = ( 3,1), = (2, ),且 与 垂直,则实数 =______.
7.在数列{ }中, 1 = 2, +1 = 2( ∈ , ≥ 1),则 5 = ______.
3
8.设 = , ∈ ( , ),则 的值为 .
5 2
9.命题:若直线 与平面 上的无数条直线垂直,则 ⊥ ,是______命题(选填“真”或“假”).
10.向量 = (3,5)在向量 = (1,1)方向上的数量投影为______.
11.正方体 1 1 1 1中,二面角 1 1的大小为______.
12.数列{ }中,其前 项和 =
2 + 2 ,则 5 = ______.
1
13.已知无穷数列{ }满足 +1 = ( 为正整数),且
∞
2 = 1,记 为数列{ }的前 项和,则∑ =1 = 2
______.
14.给出以下四个命题:
①如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线和交线平行;
第 1 页,共 6 页
②如果一条直线和一个平面上的两条相交直线都垂直,那么这条直线垂直于这个平面;
③如果两条直线都平行于一个平面,那么这两条直线互相平行;
④ 、 与平面 成角相等,则 // .
其中是真命题的有______.
15.在数列{ }中, 1 = 6,且 = 1 + lg ( ≥ 2),则 100 = ______. 1
16.如图,在直四棱柱 1 1 1 1中,底面 为菱形,且∠ = 60°.
若 = 1 = 2,点 为棱 1的中点,点 在 1 上,则线段 , 的长度
和的最小值为______.
三、解答题:本题共 5 小题,共 60 分。解答应写出文字说明,证明过程或演算步骤。
17.(本小题12分)
已知函数 ( ) = .
(1)求 ( )的最小正周期;
(2)求 ( )在区间[ , ]上的最大值和最小值.
6 3
18.(本小题12分)
已知{ }是等差数列,{ }是等比数列,且 2 = 3, 3 = 9, 1 = 1, 14 = 4.
(1)求{ }的通项公式;
(2)设 = + ,求数列{ }的前 项和.
19.(本小题12分)
据《黑鞑事略》记载:“穹庐有二样:燕京之制,用柳木为骨,正如南方罘思,可以卷舒,面前开门,上
如伞骨,顶开一窍,谓之天窗,皆以毡为衣,马上可载.草地之制,以柳木组定成硬圈,径用毡挞定,不可
卷舒,车上载行.”随着畜牧业经济的发展和牧民生活的改善,穹庐或毡帐逐渐被蒙古包代替.一个普通的蒙
古包可视为一个圆锥与一个圆柱的组合体.如图,已知该圆锥的高为3米,圆柱的高为4米,底面直径为8米.
第 2 页,共 6 页
(1)求该蒙古包的表面积(不含底面);
(2)求该蒙古包的体积.
20.(本小题12分)
如图,正方体的棱长为1, ′ ∩ ′ = ,求:
(1) 与 ′ ′所成角的大小;
(2) 与平面 所成角的正切值.
21.(本小题12分)
如图,三棱柱 1 1 1中,底面为正三角形, 1 ⊥平面 ,且 1 = = 3, 是 的中点.
(Ⅰ)求证: 1 //平面 1;
(Ⅱ)求证:平面 1 ⊥平面 1;
9
(Ⅲ)在侧棱 1上是否存在一点 ,使得三棱锥 的体积是 ,若存在,求 长;若不存在,说明理由. 8
第 3 页,共 6 页
1.【答案】
2.【答案】
3.【答案】
4.【答案】
5.【答案】5
6.【答案】 6
7.【答案】6
3
8.【答案】
4
9.【答案】假
10.【答案】4√ 2
11.【答案】45°
12.【答案】11
13.【答案】4
14.【答案】①②
15.【答案】8
16.【答案】√ 9 + 2√ 10
1 2
17.【答案】解:(1) ( ) = 2 , = = ,则 ( )的最小正周期为 .
2 2
2 √ 3 √ 3 1 1
(2) ≤ ≤ ,则 ≤ 2 ≤ , ≤ 2 ≤ 1, ≤ 2 ≤ .
6 3 3 3 2 4 2 2
1 √ 3
所以 ( )在[ , ]上的最大值为 ,最小值为 .
6 3 2 4
18.【答案】解:(1)设{ }是公差为 的等差数列,{ }是公比为 的等比数列,
由 32 = 3, 3 = 9,可得 = = 3, 2
= · 2 = 3 · 3 2 2 = 3
1;
即有 1 = 1 = 1, 14 = 4 = 27,
则 = 14 1 = 2,
13
则 = 1 + ( 1) = 1 + 2( 1) = 2 1;
(2) = +
1
= 2 1 + 3 ,
第 4 页,共 6 页
则数列{ }的前 项和为:
[1 + 3 + + (2 1)] + (1 + 3 + 9 + + 3 1)
2 1 3
= · +
2 1 3
3 1
= 2 + .
2
19.【答案】解:(1) ∵蒙古包可视为一个圆锥与一个圆柱的组合体,
且该圆锥的高为3米,圆柱的高为4 ,底面直径为8 ,
∴ = √ 32 + 42 = 5,又 = 4,
1
故该蒙古包的表面积为 × 8 × 5 + 8 × 4 = 52 ( 2);
2
(2)由题意可得该蒙古包的体积为:
1 1
× 2 × + × 2 × = × 48 + 64 = 80 ( 3).
3 3
20.【答案】解:(1) ∵ ′ ′// ,
∴ 与 ′ ′所成的角就是∠ .
∵ ⊥平面 ′, 平面 ′,
∴ ⊥ ,
又 ⊥ , ∩ = , , 平面 ,
∴ ⊥平面 .
又 平面 ,∴ ⊥ ,
1
在 △ 中, √ 2 = , = √ 2,sin∠ = = ,
2 2
∴ ∠ = 30°.
即 与 ′ ′所成角为30°.
(2)如图,作 ⊥ 于 ,连接 .
∵平面 ′ ⊥平面 ,平面 ′ ∩平面 = , 平面 ′,
∴ ⊥平面 ,
∴ ∠ 为 与平面 所成的角.
1
在 △ 中, = , 1 √ 5
2 = √ 1
2 + ( )2 = ,
2 2
√ 5
∴ tan∠ = = .
5
即 与平面 所成角的正切值为√ 5.
5
第 5 页,共 6 页
(3)由(1)可知 ⊥平面 .
又∵ 平面 ,∴平面 ⊥平面 .
即平面 与平面 所成的角为90°.
21.【答案】解:(Ⅰ)连接 1 交 1于点 ,连接 .
∵三棱柱 1 1 1中, 1 ⊥平面 ,
∴四边形 1 1为矩形,可得点 为 1 的中点.
∵ 为 中点,得 为△ 1 中位线,
∴ 1 // .
∵ 平面 1, 1 平面 1,
∴ 1 //平面 1. … (4分)
(Ⅱ) ∵底面 正三角形, 是 的中点
∴ ⊥
∵ 1 ⊥平面 , 平面 ,∴ 1 ⊥ .
∵ 1 ∩ = ,∴ ⊥平面 1,
∵ 平面 1,∴平面 1 ⊥平面 1. … (9分)
9
(Ⅲ)假设在侧棱 1上存在一点 ,使三棱锥 的体积是 ,设 = 8
∵三棱锥 的体积 =
1 1 9
,得1 1 3 3√ 3 9∴ × × × × = × × × × = .
3 2 8 3 2 2 2 8
∴ = √ 3,即 = √ 3
9
∴在侧棱 1上存在一点 ,当 = √ 3时,三棱锥 的体积是 . … (14分) 8
第 6 页,共 6 页
同课章节目录
