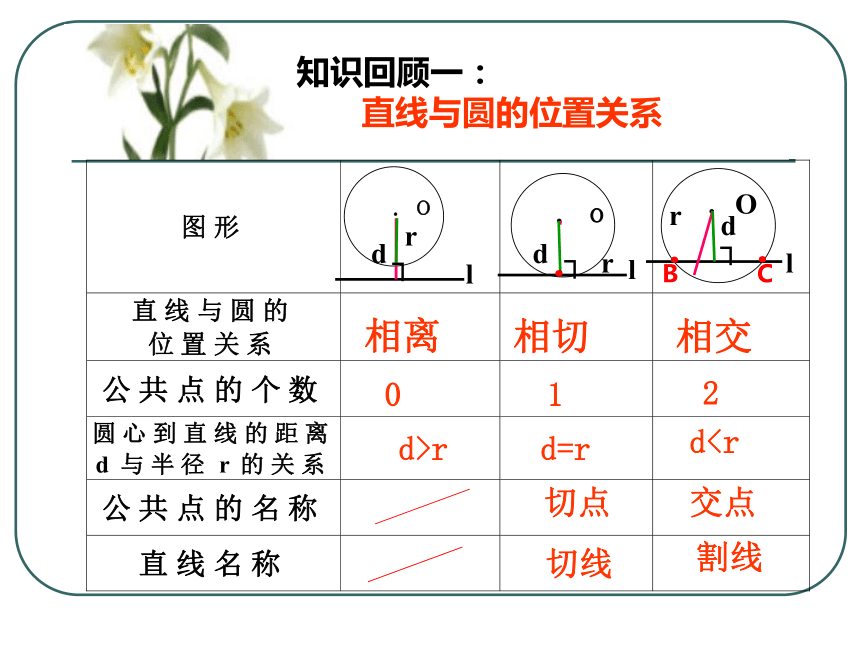
直线与圆的位置关系

课件24张PPT。直线与圆的位置关系复习课知识回顾一：
直线与圆的位置关系．Ｏldr┐0d>r相离 1d=r切点切线┐．ｏldr.相切 2d 小试身手3)若AB和⊙O相交,则 .2、已知⊙O的半径为5cm, 圆心O与直线AB的距离为d,
根据条件填写d的范围:
1)若AB和⊙O相离,则 ;
2)若AB和⊙O相切,则 ;d > 5cmd = 5cmd < 5cm小试身手例题欣赏在Rt△ABC中，∠C=90°，AC=3cm，BC=4cm，以C为圆心，r为半径的圆与AB有怎样的位置关系？为什么？
（1）r=2cm；（2）r=2.4cm (3)r=3cm．分析：要了解AB与⊙C的位置关系，只要知道圆心C到AB的距离d与r的关系．已知r，只需求出C到AB的距离d。怎样求？图上有没有？如何作出？方法总结判定直线与圆的位置关系的方法有____种：（1）根据定义，由___________________________来判断；（2）根据性质，由___________________________的关系来判断。在实际应用中，常采用第二种方法判定。两直线与圆的公共点的个数圆心到直线的距离d与半径r
知识回顾二：
圆的切线判定判定一条直线是圆的切线的三种方法:１、利用定义：与圆有唯一公共点的直线是圆的切线。２、利用数量关系：与圆心距离等与圆的半径的直线
是圆的切线。３、经过半径的外端并且垂直于这条半径的直线是圆
的切线。２、填空：
在三角形OAB中,若OA=4,OB=4,圆O的半径是2,则当
∠AOB=________时,直线AB与圆O相切。 １、选择：下列直线能判定为圆的切线是（　）
　　　　　　A、与圆有公共点的直线　　　　
　　　　　　B、垂直于圆的半径的直线
　　　　　　C、过圆的半径外端的直线　　　
　　　　　　D、到圆心的距离等于该圆半径的直线D120度小试身手例题欣赏３、证明题：
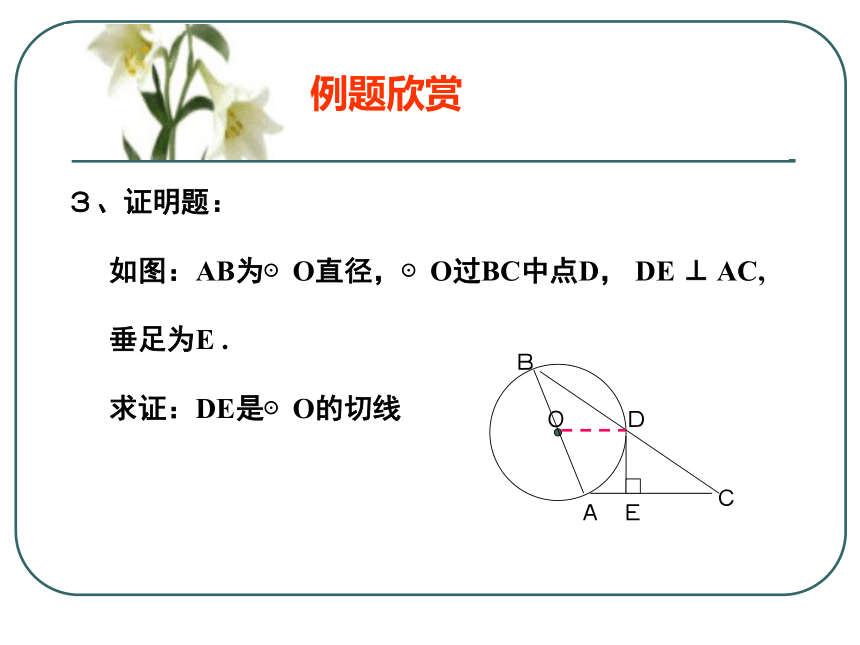
如图：AB为⊙O直径，⊙O过BC中点D， DE ⊥ AC,　
垂足为E .
求证：DE是⊙O的切线如图，AB是⊙O的直径，弦AD平分∠BAC，
过A作AC⊥DC，
求证：DC是⊙O的切线。思维拓展？知识回顾三：
三角形的外接圆与内切圆的比较1、什么是三角形的外接圆与内切圆？
2、如何画出一个三角形的外接圆与内切圆？画圆的关键： 1、确定圆心 2、确定半径 三角形的外接圆的圆心是各边垂直平分线的交点；其半径是交点到顶点的距离。 三角形的内切圆的圆心是各内角平分线的交点；其半径是交点到一边的距离。 ①经过三角形各顶点的圆叫三角形的外接圆。
　②与三角形各边都相切的圆叫三角形的内切圆。填一填，选一选1、 如图1，△ABC是⊙O的 三角形。⊙ O是△ABC的
______圆，点O叫△ABC的 ，它是三角形 _____________的交点。外接内接外心三边垂直平分线2、如图2，△DEF是⊙I的 三角形， ⊙I是△DEF的 圆，点I是 △DEF的_____ 心，它是________的交点。外切内切内角平分线3、三角形的内心到三角形各个顶点的距离相等( )
4、三角形的外心到三角形各边的距离相等 （ ）
5、等边三角形的内心和外心重合； （ ）
6、三角形的内心一定在三角形的内部（ ）错错对 对在△ABC中，内切圆O与边BC、CA、AB分别相切于点D、E、
F，∠B=60度， ∠C=70度，求∠EDF的度数OAFEDCB已知：点I是△ABC的内心，AI交BC于D，交外接圆于E。
求证：EB=EI=EC ABCIDE12345例题欣赏总结：三角形的内心、外心比较知识回顾四：
切线长定理切线长定理：
从圆外一点引圆的两条切线，它们的切线长相等，这点和圆心的连线平分两条切线的夹角．几何语言：
∵PA、PB是⊙O的切线，A、B为切点，
∴PA=PB，∠APO=∠BPO（第1题）练一练1.如图，AB、AC、BD是⊙O的切线，P、C、D为切点.如果AB=5，AC=3，你还能得出什么结论？为什么？2.如图，PA、PB是⊙O的切线，A、B为切点.如果⊙O的半径为5，∠APO=30°，你还有什么新的发现？说明理由.1、已知⊙O的半径为R，点A在直线L上，点A到⊙O的圆心O
的距离为R，则L与⊙O的公共点的个数是 _______ 。1个··OOAALL或2个综合能力检测2、已知：O为△ABC的外心，
若∠A= 80 度 则 ∠BOC= ；
若∠A= α
则 ∠BOC= 。 160°2 α 或 360 °- 2α综合能力检测综合能力检测3、在等腰△ABC中，AB=AC=2cm，若以A为圆心，1cm为半径的圆与BC相切，则∠ABC的度数为（ ）
A、30° B、60° C、90° D、120°A综合能力检测4、在梯形ABCD中,AD∥BC,∠BCD=90°,以CD为直径的圆
与AB相切于点E,S梯形ABCD=21cm2,周长为20cm,则半圆的半
径为( )
A.3cm; B.7cm;
C.3cm或7cm; D.2cmA综合能力检测船有无触礁的危险 海中有一个小岛P,该岛四周12海里内暗礁.今有货轮四由西向东航行,开始在A点观测P在北偏东600处, 行驶10海里后到达B点观测P在北偏东450处,货轮继续向东航行.要解决这个问题,我们可以将其数学化,如图:请与同伴交流你是怎么想的? 怎么去做?你认为货轮继续向东航行途中会有触礁的危险吗?综合能力检测如图，一热带风暴中心O距A岛为2千米，风暴影响圈的半径为1千米.有一条船从A岛出发沿AB方向航行，问∠BAO的度数是多少时船就会进入风暴影响圈？课堂小结：
谈谈你本节课的收获！