湘教版数学七年级下册2024-2025学年数学七年级下册期末综合测试卷(一)(含答案)
文档属性
| 名称 | 湘教版数学七年级下册2024-2025学年数学七年级下册期末综合测试卷(一)(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 193.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-09 13:25:01 | ||
图片预览



文档简介
期末综合测试卷(一)
时间:120 分钟 满分:120分
题 号 一 二 三 总 分
得 分
一、选择题(本大题共12小题,每小题2分,共24分)
1.《九章算术》中有注:“今两算得失相反,要令正负以名之.”意思是:“今有两数若其意义相反,则分别叫做正数和负数.”如果水位升高5米记为+5米,那么水位下降3 米应记为 ( )
A. - 5米 B. +5米 C. - 2米 D. -3米
2. 下列各式: 中多项式有 ( )
A.2个 B.3个 C.4个 D.5个
3. 下列计算正确的是 ( )
A.0-2=2
4. 如图,下列说法正确的是 ( )
A. 点O 在射线AB 上 B. 点 B 是直线AB 的一个端点
C. 射线 OB 和射线AB 是同一条射线 D. 点A 在线段OB 上
5. 为了解某中学七年级560名学生的身高情况,抽查了其中80名学生的身高进行统计分析.下面叙述正确的是 ( )
A.560名学生是总体 B. 每名学生是总体的一个个体
C.80名学生的身高是总体的一个样本 D. 此次调查属于全面调查
6. 在我国南海某域探明可燃冰储量约有194 亿 m ,数字19 400 000 000用科学记数法表示正确的是 ( )
7. 在钟表上,1点30分时,时针与分针所成的角是 ( )
A.150° B.165° C.135° D.120°
8. 某校组建了46人的合唱队和30人的舞蹈队参加文艺演出,现根据演出需要,从舞蹈队中抽调了部分同学参加合唱队,使合唱队的人数恰好是舞蹈队人数的3倍.设从舞蹈队中抽调了x人参加合唱队,可得正确的方程是 ( )
A.46+x=3(30-x) B.3(46-x)=30+x
C.46-3x=30+x D.46-x=3(30-x)
9. 若方程3x+6=12的解也是方程6x+3a=24的解,则a的值为 ( )
A. B.4 C.12 D.2
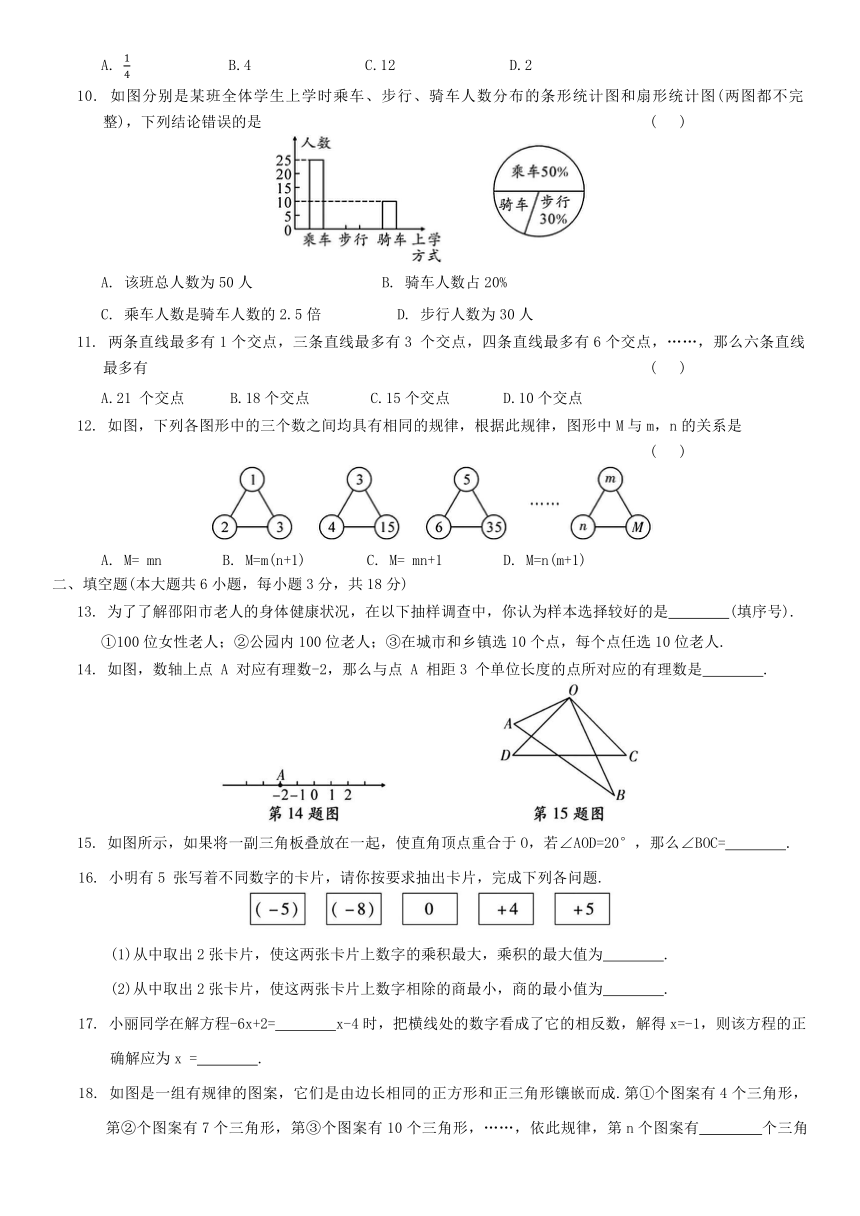
10. 如图分别是某班全体学生上学时乘车、步行、骑车人数分布的条形统计图和扇形统计图(两图都不完整),下列结论错误的是 ( )
A. 该班总人数为50人 B. 骑车人数占20%
C. 乘车人数是骑车人数的2.5倍 D. 步行人数为30人
11. 两条直线最多有1个交点,三条直线最多有3 个交点,四条直线最多有6个交点,……,那么六条直线最多有 ( )
A.21 个交点 B.18个交点 C.15个交点 D.10个交点
12. 如图,下列各图形中的三个数之间均具有相同的规律,根据此规律,图形中M与m,n的关系是 ( )
A. M= mn B. M=m(n+1) C. M= mn+1 D. M=n(m+1)
二、填空题(本大题共6小题,每小题3分,共18分)
13. 为了了解邵阳市老人的身体健康状况,在以下抽样调查中,你认为样本选择较好的是 (填序号).
①100位女性老人;②公园内100位老人;③在城市和乡镇选10个点,每个点任选10位老人.
14. 如图,数轴上点 A 对应有理数-2,那么与点 A 相距3 个单位长度的点所对应的有理数是 .
15. 如图所示,如果将一副三角板叠放在一起,使直角顶点重合于O,若∠AOD=20°,那么∠BOC= .
16. 小明有5 张写着不同数字的卡片,请你按要求抽出卡片,完成下列各问题.
(1)从中取出2张卡片,使这两张卡片上数字的乘积最大,乘积的最大值为 .
(2)从中取出2张卡片,使这两张卡片上数字相除的商最小,商的最小值为 .
17. 小丽同学在解方程-6x+2= x-4时,把横线处的数字看成了它的相反数,解得x=-1,则该方程的正确解应为x = .
18. 如图是一组有规律的图案,它们是由边长相同的正方形和正三角形镶嵌而成.第①个图案有4个三角形,第②个图案有7个三角形,第③个图案有10个三角形,……,依此规律,第n个图案有 个三角形.(用含n的代数式表示)
三、解答题(共78分)
19. (9分)计算:
20. (8分)解方程:
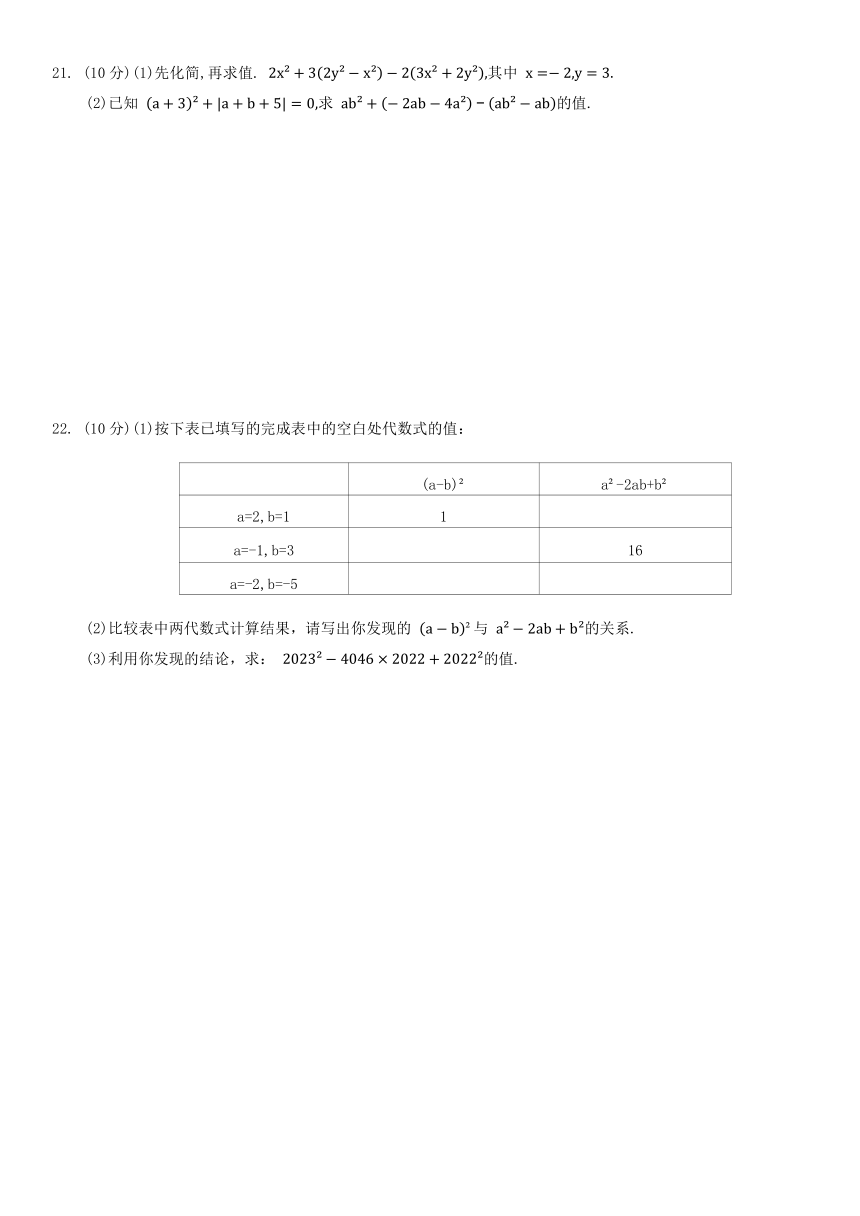
21. (10分)(1)先化简,再求值. 其中
(2)已知 求 的值.
22. (10分)(1)按下表已填写的完成表中的空白处代数式的值:
(a-b) a -2ab+b
a=2,b=1 1
a=-1,b=3 16
a=-2,b=-5
(2)比较表中两代数式计算结果,请写出你发现的 与 的关系.
(3)利用你发现的结论,求: 的值.
23. (8分)A表示一个数,若把数A写成形如 形式,其中 an都为整数.则 我们称把数A写成连分数形式.
例如:把2.8写成连分数形式的过程如下:
所以
(1)请把 写成连分数形式.
(2)有这样一个问题:如图是长为47,宽为10的长方形纸片.从中裁剪出正方形,若长方形纸片无剩余,则剪出的正方形最少是几个
小明认为这个问题和“把一个数化为连分数形式”有关联,并把 化成连分数,从而解决了问题.你可以参考小明的思路解决上述问题,请直接写出“剪出的正方形最少”时,正方形的个数.
24. (10分)安全使用电瓶车可以大幅度减少因交通事故引发的人身伤害,为此交警部门在全市范围开展了安全使用电瓶车专项宣传活动.在活动前和活动后分别随机抽取了部分使用电瓶车的市民,就骑电瓶车戴安全帽情况进行问卷调查,将收集的数据制成如下统计图表.
活动前骑电瓶车戴安全帽情况统计表
类别 人数
A 68
B 245
C 510
D 177
合计 1 000
(1)宣传活动前,在抽取的市民中哪一类别的人数最多 占抽取人数的百分之几
(2)小明认为,宣传活动后骑电瓶车“都不戴”安全帽的人数为178,比活动前增加了1人,因此交警部门开展的宣传活动没有效果.小明分析数据的方法是否合理 请结合统计图表,对小明分析数据的方法及交警部门宣传活动的效果谈谈你的看法.
25. (10分)用正方形硬纸板做三棱柱盒子,每个盒子由3 个长方形侧面和2个等边三角形底面组成,硬纸板以如图两种方法裁剪(裁剪后边角料不再利用).A方法:剪6个侧面;B方法:剪4个侧面和5个底面.
现有19张硬纸板,裁剪时x张用A方法,其余用B方法.
(1)用含x的代数式分别表示裁剪出的侧面和底面的个数.
(2)若裁剪出的侧面和底面恰好全部用完,问能做多少个盒子
26. (13分)如图1,B 是线段AD 上一动点,沿A→D→A 的路线以 的速度往返运动1次,C是线段BD的中点, 设点 B 的运动时间为
(1)当 时,则线段 线段
(2)用含t的式子表示运动过程中AB 的长.
(3)在运动过程中,若AB的中点为E,问EC的长是否变化 与点 B 的位置是否无关
(4)知识迁移:如图2,已知, ,过角的内部任一点 B画射线OB,若OE,OC 分别平分 和 问 的度数是否变化 与射线 OB 的位置是否无关
期末综合测试卷(一)
1. D 2. B 3. D 4. D 5. C 6. A 7. C 8. A 9. B10. D11. C 12. B
13.③ 14. - 5 或1 15.20° 16.(1)40 (2)-2
19. 解:(1)原式
(2)原式 (3)原式
20. 解:(1)去括号,得: 移项、合并同类项,得· 系数化为1,得:
(2)去分母,得 去括号,得 移项、合并同类项,得
21. 解:(1)原式
当 时,原式
(2)原式
因为
所以
所以
因此,原式
22. 解:(1)当( 时,
当 时, 当 时,
故答案为:1;16;9;9.
(2)根据表中数据,可发现( 与 之间的关系为:
(3) 由(2)中的结论可知:
原式
解:(1)因为
所以
(2)因为
所以
所以
即当“剪出的正方形最少”时,正方形的个数为10个.
24.解:(1)宣传活动前,在抽取的市民中偶尔戴安全帽的人数最多,占抽取人数的百分比为:
(2)不合理.宣传活动后骑电瓶车“都不戴”安全帽的百分比为:
活动前骑电瓶车“都不戴”安全帽的百分比为: 因此交警部门开展的宣传活动有效果.
25. 解:(1)因为裁剪时x张用A方法,所以裁剪时( 张用B方法,所以侧面的个数为:
个,底面的个数为: 个.
(2)由题意,得 解得:
所以盒子的个数为: (个).
答:裁剪出的侧面和底面恰好全部用完,能做30个盒子.
26. 解:(1)因为 所以
因为C 是线段BD的中点,
所以
故答案为:4;3.
(2)当时,此时点 B 从A 向 D 移动: 当 时,此时点B从D向A移动:
(3)EC的长不变,与点 B 的位置无关.
因为AB中点为E,C是线段BD的中点,
所以
所以
因为 所以 与点 B 的位置无关.
(4)∠EOC 的度数不变,与射线OB的位置无关.因为OE平分∠AOB,OC平分∠BOD,所以 所以
因为∠AOD =120°,所以∠EOC=60°,与射线 OB 的位置无关.
期末综合测试卷(二)
1. B 2. C 3. D 4. D 5. B 6. B 7. D 8. C 9. B 10. B11. C 12. C
13.8 8 - 14.①② 15. - 3或5 16.55
17.5cm 或1 cm 18.5
19. 解:(1)原式
(2)原式 -20+72+104-6=150.
(3)原式=3b-2c+4a-c-3b+c=4a-2c.
(4)原式
20. 解:因为∠AOC =32°,∠AOC + ∠AOD =∠BOD +∠AOD=180°,
所以∠BOD=∠AOC=32°,所以∠AOD=148°,
因为∠DOE=∠BOD,所以∠DOE=32°,
所以∠AOE=∠AOD-∠DOE=116°,
因为OM平分∠AOE,所以
21. 解:(1)不正确;①.
(2)去分母,得3(x+1)-2(2-3x)=6,
去括号,得3x+3-4+6x=6,
移项,得
合并同类项,得9x=7,
系数化为1,得
22. 解:(1)由题意,得放入1个小球水面升高:(32-26)÷3 =2(cm),放入1个大球水面升高:(
故答案为:2;3.
(2)设应放入x个大球,则放入(10-x)个小球.
由题意,得
解得x=4,则10-x=6.
答:应放入4个大球,6个小球.
23. 解:
时间:120 分钟 满分:120分
题 号 一 二 三 总 分
得 分
一、选择题(本大题共12小题,每小题2分,共24分)
1.《九章算术》中有注:“今两算得失相反,要令正负以名之.”意思是:“今有两数若其意义相反,则分别叫做正数和负数.”如果水位升高5米记为+5米,那么水位下降3 米应记为 ( )
A. - 5米 B. +5米 C. - 2米 D. -3米
2. 下列各式: 中多项式有 ( )
A.2个 B.3个 C.4个 D.5个
3. 下列计算正确的是 ( )
A.0-2=2
4. 如图,下列说法正确的是 ( )
A. 点O 在射线AB 上 B. 点 B 是直线AB 的一个端点
C. 射线 OB 和射线AB 是同一条射线 D. 点A 在线段OB 上
5. 为了解某中学七年级560名学生的身高情况,抽查了其中80名学生的身高进行统计分析.下面叙述正确的是 ( )
A.560名学生是总体 B. 每名学生是总体的一个个体
C.80名学生的身高是总体的一个样本 D. 此次调查属于全面调查
6. 在我国南海某域探明可燃冰储量约有194 亿 m ,数字19 400 000 000用科学记数法表示正确的是 ( )
7. 在钟表上,1点30分时,时针与分针所成的角是 ( )
A.150° B.165° C.135° D.120°
8. 某校组建了46人的合唱队和30人的舞蹈队参加文艺演出,现根据演出需要,从舞蹈队中抽调了部分同学参加合唱队,使合唱队的人数恰好是舞蹈队人数的3倍.设从舞蹈队中抽调了x人参加合唱队,可得正确的方程是 ( )
A.46+x=3(30-x) B.3(46-x)=30+x
C.46-3x=30+x D.46-x=3(30-x)
9. 若方程3x+6=12的解也是方程6x+3a=24的解,则a的值为 ( )
A. B.4 C.12 D.2
10. 如图分别是某班全体学生上学时乘车、步行、骑车人数分布的条形统计图和扇形统计图(两图都不完整),下列结论错误的是 ( )
A. 该班总人数为50人 B. 骑车人数占20%
C. 乘车人数是骑车人数的2.5倍 D. 步行人数为30人
11. 两条直线最多有1个交点,三条直线最多有3 个交点,四条直线最多有6个交点,……,那么六条直线最多有 ( )
A.21 个交点 B.18个交点 C.15个交点 D.10个交点
12. 如图,下列各图形中的三个数之间均具有相同的规律,根据此规律,图形中M与m,n的关系是 ( )
A. M= mn B. M=m(n+1) C. M= mn+1 D. M=n(m+1)
二、填空题(本大题共6小题,每小题3分,共18分)
13. 为了了解邵阳市老人的身体健康状况,在以下抽样调查中,你认为样本选择较好的是 (填序号).
①100位女性老人;②公园内100位老人;③在城市和乡镇选10个点,每个点任选10位老人.
14. 如图,数轴上点 A 对应有理数-2,那么与点 A 相距3 个单位长度的点所对应的有理数是 .
15. 如图所示,如果将一副三角板叠放在一起,使直角顶点重合于O,若∠AOD=20°,那么∠BOC= .
16. 小明有5 张写着不同数字的卡片,请你按要求抽出卡片,完成下列各问题.
(1)从中取出2张卡片,使这两张卡片上数字的乘积最大,乘积的最大值为 .
(2)从中取出2张卡片,使这两张卡片上数字相除的商最小,商的最小值为 .
17. 小丽同学在解方程-6x+2= x-4时,把横线处的数字看成了它的相反数,解得x=-1,则该方程的正确解应为x = .
18. 如图是一组有规律的图案,它们是由边长相同的正方形和正三角形镶嵌而成.第①个图案有4个三角形,第②个图案有7个三角形,第③个图案有10个三角形,……,依此规律,第n个图案有 个三角形.(用含n的代数式表示)
三、解答题(共78分)
19. (9分)计算:
20. (8分)解方程:
21. (10分)(1)先化简,再求值. 其中
(2)已知 求 的值.
22. (10分)(1)按下表已填写的完成表中的空白处代数式的值:
(a-b) a -2ab+b
a=2,b=1 1
a=-1,b=3 16
a=-2,b=-5
(2)比较表中两代数式计算结果,请写出你发现的 与 的关系.
(3)利用你发现的结论,求: 的值.
23. (8分)A表示一个数,若把数A写成形如 形式,其中 an都为整数.则 我们称把数A写成连分数形式.
例如:把2.8写成连分数形式的过程如下:
所以
(1)请把 写成连分数形式.
(2)有这样一个问题:如图是长为47,宽为10的长方形纸片.从中裁剪出正方形,若长方形纸片无剩余,则剪出的正方形最少是几个
小明认为这个问题和“把一个数化为连分数形式”有关联,并把 化成连分数,从而解决了问题.你可以参考小明的思路解决上述问题,请直接写出“剪出的正方形最少”时,正方形的个数.
24. (10分)安全使用电瓶车可以大幅度减少因交通事故引发的人身伤害,为此交警部门在全市范围开展了安全使用电瓶车专项宣传活动.在活动前和活动后分别随机抽取了部分使用电瓶车的市民,就骑电瓶车戴安全帽情况进行问卷调查,将收集的数据制成如下统计图表.
活动前骑电瓶车戴安全帽情况统计表
类别 人数
A 68
B 245
C 510
D 177
合计 1 000
(1)宣传活动前,在抽取的市民中哪一类别的人数最多 占抽取人数的百分之几
(2)小明认为,宣传活动后骑电瓶车“都不戴”安全帽的人数为178,比活动前增加了1人,因此交警部门开展的宣传活动没有效果.小明分析数据的方法是否合理 请结合统计图表,对小明分析数据的方法及交警部门宣传活动的效果谈谈你的看法.
25. (10分)用正方形硬纸板做三棱柱盒子,每个盒子由3 个长方形侧面和2个等边三角形底面组成,硬纸板以如图两种方法裁剪(裁剪后边角料不再利用).A方法:剪6个侧面;B方法:剪4个侧面和5个底面.
现有19张硬纸板,裁剪时x张用A方法,其余用B方法.
(1)用含x的代数式分别表示裁剪出的侧面和底面的个数.
(2)若裁剪出的侧面和底面恰好全部用完,问能做多少个盒子
26. (13分)如图1,B 是线段AD 上一动点,沿A→D→A 的路线以 的速度往返运动1次,C是线段BD的中点, 设点 B 的运动时间为
(1)当 时,则线段 线段
(2)用含t的式子表示运动过程中AB 的长.
(3)在运动过程中,若AB的中点为E,问EC的长是否变化 与点 B 的位置是否无关
(4)知识迁移:如图2,已知, ,过角的内部任一点 B画射线OB,若OE,OC 分别平分 和 问 的度数是否变化 与射线 OB 的位置是否无关
期末综合测试卷(一)
1. D 2. B 3. D 4. D 5. C 6. A 7. C 8. A 9. B10. D11. C 12. B
13.③ 14. - 5 或1 15.20° 16.(1)40 (2)-2
19. 解:(1)原式
(2)原式 (3)原式
20. 解:(1)去括号,得: 移项、合并同类项,得· 系数化为1,得:
(2)去分母,得 去括号,得 移项、合并同类项,得
21. 解:(1)原式
当 时,原式
(2)原式
因为
所以
所以
因此,原式
22. 解:(1)当( 时,
当 时, 当 时,
故答案为:1;16;9;9.
(2)根据表中数据,可发现( 与 之间的关系为:
(3) 由(2)中的结论可知:
原式
解:(1)因为
所以
(2)因为
所以
所以
即当“剪出的正方形最少”时,正方形的个数为10个.
24.解:(1)宣传活动前,在抽取的市民中偶尔戴安全帽的人数最多,占抽取人数的百分比为:
(2)不合理.宣传活动后骑电瓶车“都不戴”安全帽的百分比为:
活动前骑电瓶车“都不戴”安全帽的百分比为: 因此交警部门开展的宣传活动有效果.
25. 解:(1)因为裁剪时x张用A方法,所以裁剪时( 张用B方法,所以侧面的个数为:
个,底面的个数为: 个.
(2)由题意,得 解得:
所以盒子的个数为: (个).
答:裁剪出的侧面和底面恰好全部用完,能做30个盒子.
26. 解:(1)因为 所以
因为C 是线段BD的中点,
所以
故答案为:4;3.
(2)当时,此时点 B 从A 向 D 移动: 当 时,此时点B从D向A移动:
(3)EC的长不变,与点 B 的位置无关.
因为AB中点为E,C是线段BD的中点,
所以
所以
因为 所以 与点 B 的位置无关.
(4)∠EOC 的度数不变,与射线OB的位置无关.因为OE平分∠AOB,OC平分∠BOD,所以 所以
因为∠AOD =120°,所以∠EOC=60°,与射线 OB 的位置无关.
期末综合测试卷(二)
1. B 2. C 3. D 4. D 5. B 6. B 7. D 8. C 9. B 10. B11. C 12. C
13.8 8 - 14.①② 15. - 3或5 16.55
17.5cm 或1 cm 18.5
19. 解:(1)原式
(2)原式 -20+72+104-6=150.
(3)原式=3b-2c+4a-c-3b+c=4a-2c.
(4)原式
20. 解:因为∠AOC =32°,∠AOC + ∠AOD =∠BOD +∠AOD=180°,
所以∠BOD=∠AOC=32°,所以∠AOD=148°,
因为∠DOE=∠BOD,所以∠DOE=32°,
所以∠AOE=∠AOD-∠DOE=116°,
因为OM平分∠AOE,所以
21. 解:(1)不正确;①.
(2)去分母,得3(x+1)-2(2-3x)=6,
去括号,得3x+3-4+6x=6,
移项,得
合并同类项,得9x=7,
系数化为1,得
22. 解:(1)由题意,得放入1个小球水面升高:(32-26)÷3 =2(cm),放入1个大球水面升高:(
故答案为:2;3.
(2)设应放入x个大球,则放入(10-x)个小球.
由题意,得
解得x=4,则10-x=6.
答:应放入4个大球,6个小球.
23. 解:
同课章节目录
