1.2.1有理数的概念 学案(无答案) 人教版(2024)数学七年级上册
文档属性
| 名称 | 1.2.1有理数的概念 学案(无答案) 人教版(2024)数学七年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 81.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-09 20:45:12 | ||
图片预览

文档简介
课题:1.2.1有理数的概念
【学习目标】
了解正数、负数、有理数的概念;
2、通过对生活实例中数的特征去认识正数和负数的定义;
3、能用正数和负数去表示相反意义的量,体会其中符号化的方法.
【评价目标】1、自我检查:能用自己的语言说出有理数的概念。
2、对话展示:能辨别整数、分数,正整数、负整数,正分数、负分数等。
3、课堂提问:能说出有理数的两种分类。
4、纸笔作业:能对各种有理数做出归类总结。
【学习重难点】有理数的概念、分类。
【学习过程】
一、【温故 习新】
(一)创设情境
1、6,2005,,0,-3,+1,,-6.8中,正整数和负分数共有 个
2、在0,1,-2,-3.5这四个数中,是负整数的是
3、什么是有理数?
(二)探索新知
4、下列说法中正确的序号是 .①零是整数;②零是有理数;③零是自然数;④零是正数;⑤零是负数;⑥零是非负数。
5、列说法中,错误的有( )
①是负分数;②1.5不是整数;③非负有理数不包括0;④整数和分数统称为有理数;⑤0是最小的有理数;⑥-1是最小的负整数。
A、1个 B、2个 C、3个 D、4个
二、【研讨 拓展】
(一)巩固新知
例1、把下列各数填入相应的集合内:
,3.1416,0,2004,-,-0.23456,10%,10.l,0.67,-89
正数集合 负数集合 整数集合 分数集合
巩固练习:把下面的有理数填入它属于的集合内:
,,,,0.1,,,0,123,2.333
正数集合:{ …} 负数集合:{ …}
分数集合:{ …} 非负整数集合:{ …}
(二)能力提升
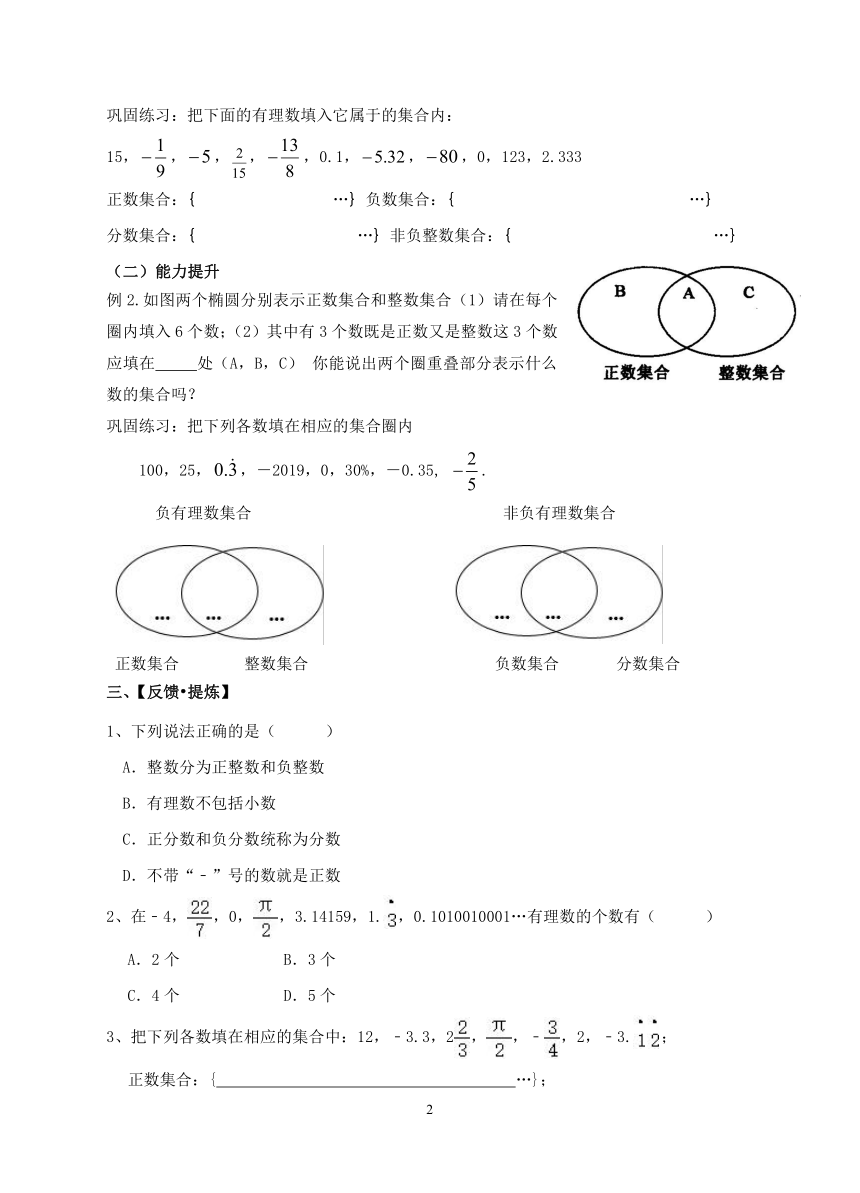
例2.如图两个椭圆分别表示正数集合和整数集合(1)请在每个圈内填入6个数;(2)其中有3个数既是正数又是整数这3个数应填在 处(A,B,C)你能说出两个圈重叠部分表示什么数的集合吗?
巩固练习:把下列各数填在相应的集合圈内
100,25,,-2019,0,30%,-0.35, .
负有理数集合 非负有理数集合
正数集合 整数集合 负数集合 分数集合
三、【反馈 提炼】
1、下列说法正确的是( )
A.整数分为正整数和负整数
B.有理数不包括小数
C.正分数和负分数统称为分数
D.不带“﹣”号的数就是正数
2、在﹣4,,0,,3.14159,1.,0.1010010001…有理数的个数有( )
A.2个 B.3个
C.4个 D.5个
3、把下列各数填在相应的集合中:12,﹣3.3,2,,﹣,2,﹣3.;
正数集合:{ …};
非负整数集合:{ …};
分数集合:{ …}.
4、在有理数中最大的负整数是 ,最小的非负数 .
【课堂小结】
思维导图:
1、有理数的概念
① 、 、 统称为整数。
② 、 统称为分数。
③整数和分数统称为 。
2、有理数的两大分类:按定义或按正负
★ 或
3、数的集合:把一些数放在一起,就组成一个数的集合,简称数集.所有的有理数组成的数集叫做有理数集,所有整数组成的数集叫做整数集。
【每日一题】(2020 湖里区)如图,已知A是整数集合,B是正数集合,C是分数集合,D是A和B的重叠部分,E是B和C的重叠部分.
(Ⅰ)D是 集合,E是 集合;
(Ⅱ)给出下列各数:10,﹣0.72,﹣98,25,,63%,﹣3.14,请将它们填入图2中相应的集合中去.
【课后作业】
[基础巩固]
1、下列说法正确的有
①任何有理数都有倒数②所有整数都是正数③所有的分数都是有理数④零既不是正数也不是负数,但它是整数
2、下列说法错误的是( ).
A.-0.5是分数 B.0不是正数也不是负数,但是自然数 C.-3.27是负分数 D.非负数就是正数
[能力发展]
3、正整数集合与负整数集合合并在一起构成的集合是( ).
A.整数集合 B.有理数集合 C.自然数集合 D.以上说法都不对
4、把下列各数放在相应的集合中.
-100,-0.082,-30,3.14,-3,0,-27,-,,1,
整数集合{ …};分数集合{ …};
正数集合{ …};负数集合{ …};
正整数集合{ …};负整数集合{ …};
正分数集合{ …};负分数集合{ …};
非正数集合{ …}.
[综合实践]
5、将下列各数填入相应的集合圈内:
+2.8,-900,-0.5,-7,-,99.9,0,4.(注意:正确理解重叠部分的含义)
整数集合 正数集合 负数集合 分数集合
【学习目标】
了解正数、负数、有理数的概念;
2、通过对生活实例中数的特征去认识正数和负数的定义;
3、能用正数和负数去表示相反意义的量,体会其中符号化的方法.
【评价目标】1、自我检查:能用自己的语言说出有理数的概念。
2、对话展示:能辨别整数、分数,正整数、负整数,正分数、负分数等。
3、课堂提问:能说出有理数的两种分类。
4、纸笔作业:能对各种有理数做出归类总结。
【学习重难点】有理数的概念、分类。
【学习过程】
一、【温故 习新】
(一)创设情境
1、6,2005,,0,-3,+1,,-6.8中,正整数和负分数共有 个
2、在0,1,-2,-3.5这四个数中,是负整数的是
3、什么是有理数?
(二)探索新知
4、下列说法中正确的序号是 .①零是整数;②零是有理数;③零是自然数;④零是正数;⑤零是负数;⑥零是非负数。
5、列说法中,错误的有( )
①是负分数;②1.5不是整数;③非负有理数不包括0;④整数和分数统称为有理数;⑤0是最小的有理数;⑥-1是最小的负整数。
A、1个 B、2个 C、3个 D、4个
二、【研讨 拓展】
(一)巩固新知
例1、把下列各数填入相应的集合内:
,3.1416,0,2004,-,-0.23456,10%,10.l,0.67,-89
正数集合 负数集合 整数集合 分数集合
巩固练习:把下面的有理数填入它属于的集合内:
,,,,0.1,,,0,123,2.333
正数集合:{ …} 负数集合:{ …}
分数集合:{ …} 非负整数集合:{ …}
(二)能力提升
例2.如图两个椭圆分别表示正数集合和整数集合(1)请在每个圈内填入6个数;(2)其中有3个数既是正数又是整数这3个数应填在 处(A,B,C)你能说出两个圈重叠部分表示什么数的集合吗?
巩固练习:把下列各数填在相应的集合圈内
100,25,,-2019,0,30%,-0.35, .
负有理数集合 非负有理数集合
正数集合 整数集合 负数集合 分数集合
三、【反馈 提炼】
1、下列说法正确的是( )
A.整数分为正整数和负整数
B.有理数不包括小数
C.正分数和负分数统称为分数
D.不带“﹣”号的数就是正数
2、在﹣4,,0,,3.14159,1.,0.1010010001…有理数的个数有( )
A.2个 B.3个
C.4个 D.5个
3、把下列各数填在相应的集合中:12,﹣3.3,2,,﹣,2,﹣3.;
正数集合:{ …};
非负整数集合:{ …};
分数集合:{ …}.
4、在有理数中最大的负整数是 ,最小的非负数 .
【课堂小结】
思维导图:
1、有理数的概念
① 、 、 统称为整数。
② 、 统称为分数。
③整数和分数统称为 。
2、有理数的两大分类:按定义或按正负
★ 或
3、数的集合:把一些数放在一起,就组成一个数的集合,简称数集.所有的有理数组成的数集叫做有理数集,所有整数组成的数集叫做整数集。
【每日一题】(2020 湖里区)如图,已知A是整数集合,B是正数集合,C是分数集合,D是A和B的重叠部分,E是B和C的重叠部分.
(Ⅰ)D是 集合,E是 集合;
(Ⅱ)给出下列各数:10,﹣0.72,﹣98,25,,63%,﹣3.14,请将它们填入图2中相应的集合中去.
【课后作业】
[基础巩固]
1、下列说法正确的有
①任何有理数都有倒数②所有整数都是正数③所有的分数都是有理数④零既不是正数也不是负数,但它是整数
2、下列说法错误的是( ).
A.-0.5是分数 B.0不是正数也不是负数,但是自然数 C.-3.27是负分数 D.非负数就是正数
[能力发展]
3、正整数集合与负整数集合合并在一起构成的集合是( ).
A.整数集合 B.有理数集合 C.自然数集合 D.以上说法都不对
4、把下列各数放在相应的集合中.
-100,-0.082,-30,3.14,-3,0,-27,-,,1,
整数集合{ …};分数集合{ …};
正数集合{ …};负数集合{ …};
正整数集合{ …};负整数集合{ …};
正分数集合{ …};负分数集合{ …};
非正数集合{ …}.
[综合实践]
5、将下列各数填入相应的集合圈内:
+2.8,-900,-0.5,-7,-,99.9,0,4.(注意:正确理解重叠部分的含义)
整数集合 正数集合 负数集合 分数集合
同课章节目录
