3.2 热力学第一定律课件(18张PPT)
文档属性
| 名称 | 3.2 热力学第一定律课件(18张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 283.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2025-01-08 13:50:02 | ||
图片预览






文档简介
(共18张PPT)
3.2 热力学第一定律
人教版选择性必修第三册同步课件
汽缸内有一定质量的气体,压缩气体的同时给汽缸加热。那么,气体内能的变化会比单一方式(做功或传热)更明显。这是为什么呢
压缩气体,内能增大,给气体加热内能也是增大。两者叠加所以就更明显。
知识点一:热力学第一定律
1.内容:一个热力学系统的内能增量等于外界向它传递的热量与对它所做的功的和。
2.表达式:
ΔU= Q + W
热传递的热量
做功
内能的改变量
3.意义:热力学第一定律反映了功、热量跟系统内能改变之间的定量关系.
思考与讨论:一定质量的气体,膨胀过程中是外界对气体做功还是气体对外界做功?如果膨胀时气体对外做的功是135 J,同时向外放热85J,气体内能的变化量是多少?内能是增加了还是减少了?请你通过这个例子总结功和热量取正、负值的物理意义。
解:
气体对外界做功
系统对外做功:W=-135J
系统向外放热:Q=-85J
ΔU = W + Q
代入得:
ΔU =-135+(-85)
=-220J
内能变化了220J,减少
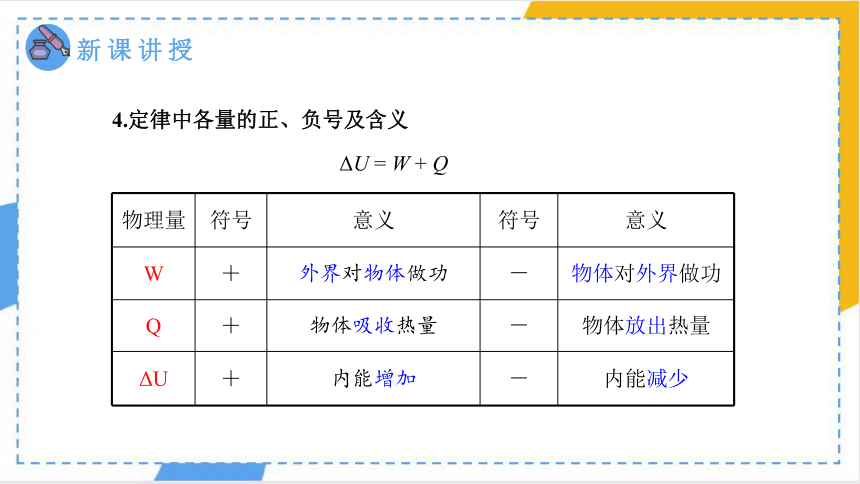
4.定律中各量的正、负号及含义
物理量 符号 意义 符号 意义
W + 外界对物体做功 - 物体对外界做功
Q + 物体吸收热量 - 物体放出热量
ΔU + 内能增加 - 内能减少
ΔU = W + Q
5.判断是否做功的方法
一般情况下外界对物体做功与否,需看物体的体积是否变化。
(1)若物体体积增大,表明物体对外界做功,W<0。
(2)若物体体积减小,表明外界对物体做功,W>0。
6.几种特殊情况
(1)若过程是绝热的,即Q=0,则ΔU=W,物体内能的增加量等于外界对物体做的功。
(2)若过程中不做功,即W=0,则ΔU=Q,物体内能的增加量等于物体从外界吸收的热量。
(3)若过程的始末状态物体的内能不变,即ΔU=0,则W=-Q(或Q=-W),外界对物体做的功等于物体放出的热量(或物体吸收的热量等于物体对外界做的功)。
知识点二:热力学第一定律的应用
热力学第一定律与理想气体状态方程结合问题的分析思路:
(1)利用体积的变化分析做功情况.气体体积增大,气体对外界做功;气体体积减小,外界对气体做功.
(2)利用温度的变化分析理想气体内能的变化.一定质量的理想气体的内能仅与温度有关,温度升高,内能增加;温度降低,内能减小.
(3)利用热力学第一定律判断是吸热还是放热.
由热力学第一定律ΔU=W+Q,则Q=ΔU-W,若已知气体的做功情况和内能的变化情况,即可判断气体状态变化是吸热过程还是放热过程
例:如图,一台四冲程内燃机,活塞在压缩冲程某段时间内移动的距离为0.1 m,这段过程活塞对气体的压力逐渐增大,其做的功相当于2× 103 N的恒力使活塞移动相同距离所做的功(图3.2-2甲)。内燃机工作时汽缸温度高于环境温度,该过程中压缩气体传递给汽缸的热量为25 J。
(1)求上述压缩过程中气体内能的变化量。
(2)燃烧后的高压气体对活塞做功,气体
推动活塞移动0.1 m,其做的功相当于
9 × 103N的恒力使活塞移动相同距离所做
的功(图3.2-2乙),该做功过程气体传递给汽缸的热量为30J,求此做功过程气体内能的变化量。
分析: 根据热力学第一定律,在第(1)问中,活塞压缩气体的过程是外界对系统做功,活塞对气体所做的功W1 为正值;在第(2)问中,气体膨胀推动活塞的过程是系统对外界做功,气体对外界所做的功W2 为负值。在两种情况下,气体都把热量传递给了汽缸,都属于放热,因此Q1、Q2 均为负值。
解:(1)压缩过程活塞对气体做的功W1= F1l1= 2 × 103×0.1 J= 200 J
气体内能的变化量ΔU1=W1+Q1=200J-25J=175J
(2)气体膨胀过程中气体对外界所做的功W2=F2l2=-9 × 103 × 0.1J=-900J
气体内能的变化量ΔU2= W2+ Q2=- 900J- 30J=- 930J
汽缸内气体在压缩过程中内能增加了175 J,在膨胀做功过程中气体内能减少了930 J。
1. 被压瘪但尚未破裂的乒乓球放在热水里泡一会儿,就会重新鼓起来,这一过程乒乓球内的气体( )
A. 吸热,对外做功,内能不变
B. 吸热,对外做功,内能增加
C. 温度升高,对外做功,内能不变
D. 压强增大,单位体积内分子数增大
B
2.根据热力学第一定律,下列说法正确的是( )
A. 电冰箱的工作过程表明,热量可以从低温物体向高温物体传递
B. 空调机在制冷过程中,从室内吸收的热量少于向室外放出的热量
C. 科技的进步可以使内燃机成为单一热源的热机
D. 对能源的过度消耗将使自然界的能量不断减少,形成能源危机
AAADFAAB
3.一定量的气体,从外界吸收热量2.7×105J,内能增加4.3×105J。在这一过程中,是气体对外做功,还是外界对气体做功?做了多少功?
Q=+2.7×105J
ΔU=+4.3×105J
﹀
ΔU=W + Q
得: W=1.6×105J >0
即外界对气体做功
解:
4.如图是用导热性能良好的材料制成的气体实验装置,开始时封闭的空气柱长度为20 cm,用竖直向下的力F压活塞,使空气柱长度变为原来的一半,人对活塞做功10 J,大气压强为p0=1×105 Pa,不计活塞的重力,求:
(1)若用足够长的时间缓慢压缩,压缩后气体的压强;
(2)若以适当的速度压缩气体,此过程气体向外散失的热量为2 J,则气体的内能增加多少?(活塞的横截面积S=1 cm2)
解:(1)设压缩后气体的压强为p,缓慢压缩,气体温度不变,由玻意耳定律:p0V0=pV
解得p=2×105 Pa。
(2)大气压力对活塞做功W1=p0SΔh=1 J,人对活塞做功W2=10 J,由热力学第一定律:ΔU=W1+W2+Q
将数据代入,解得ΔU=9 J。
热力学第一定律
热力学第一定律
表述:一个热力学系统的内能增量等于外界向它传递的热量与外界对它所做的功的和
数学表达式:ΔU= Q +W
定律中各量的正、负号及含义
热力学第一定律的应用
ΔU =0,则 W =- Q
W=0,则ΔU = Q
Q =0,则ΔU = W
热力学第一定律与理想气体状态方程结合问题的分析思路
3.2 热力学第一定律
人教版选择性必修第三册同步课件
汽缸内有一定质量的气体,压缩气体的同时给汽缸加热。那么,气体内能的变化会比单一方式(做功或传热)更明显。这是为什么呢
压缩气体,内能增大,给气体加热内能也是增大。两者叠加所以就更明显。
知识点一:热力学第一定律
1.内容:一个热力学系统的内能增量等于外界向它传递的热量与对它所做的功的和。
2.表达式:
ΔU= Q + W
热传递的热量
做功
内能的改变量
3.意义:热力学第一定律反映了功、热量跟系统内能改变之间的定量关系.
思考与讨论:一定质量的气体,膨胀过程中是外界对气体做功还是气体对外界做功?如果膨胀时气体对外做的功是135 J,同时向外放热85J,气体内能的变化量是多少?内能是增加了还是减少了?请你通过这个例子总结功和热量取正、负值的物理意义。
解:
气体对外界做功
系统对外做功:W=-135J
系统向外放热:Q=-85J
ΔU = W + Q
代入得:
ΔU =-135+(-85)
=-220J
内能变化了220J,减少
4.定律中各量的正、负号及含义
物理量 符号 意义 符号 意义
W + 外界对物体做功 - 物体对外界做功
Q + 物体吸收热量 - 物体放出热量
ΔU + 内能增加 - 内能减少
ΔU = W + Q
5.判断是否做功的方法
一般情况下外界对物体做功与否,需看物体的体积是否变化。
(1)若物体体积增大,表明物体对外界做功,W<0。
(2)若物体体积减小,表明外界对物体做功,W>0。
6.几种特殊情况
(1)若过程是绝热的,即Q=0,则ΔU=W,物体内能的增加量等于外界对物体做的功。
(2)若过程中不做功,即W=0,则ΔU=Q,物体内能的增加量等于物体从外界吸收的热量。
(3)若过程的始末状态物体的内能不变,即ΔU=0,则W=-Q(或Q=-W),外界对物体做的功等于物体放出的热量(或物体吸收的热量等于物体对外界做的功)。
知识点二:热力学第一定律的应用
热力学第一定律与理想气体状态方程结合问题的分析思路:
(1)利用体积的变化分析做功情况.气体体积增大,气体对外界做功;气体体积减小,外界对气体做功.
(2)利用温度的变化分析理想气体内能的变化.一定质量的理想气体的内能仅与温度有关,温度升高,内能增加;温度降低,内能减小.
(3)利用热力学第一定律判断是吸热还是放热.
由热力学第一定律ΔU=W+Q,则Q=ΔU-W,若已知气体的做功情况和内能的变化情况,即可判断气体状态变化是吸热过程还是放热过程
例:如图,一台四冲程内燃机,活塞在压缩冲程某段时间内移动的距离为0.1 m,这段过程活塞对气体的压力逐渐增大,其做的功相当于2× 103 N的恒力使活塞移动相同距离所做的功(图3.2-2甲)。内燃机工作时汽缸温度高于环境温度,该过程中压缩气体传递给汽缸的热量为25 J。
(1)求上述压缩过程中气体内能的变化量。
(2)燃烧后的高压气体对活塞做功,气体
推动活塞移动0.1 m,其做的功相当于
9 × 103N的恒力使活塞移动相同距离所做
的功(图3.2-2乙),该做功过程气体传递给汽缸的热量为30J,求此做功过程气体内能的变化量。
分析: 根据热力学第一定律,在第(1)问中,活塞压缩气体的过程是外界对系统做功,活塞对气体所做的功W1 为正值;在第(2)问中,气体膨胀推动活塞的过程是系统对外界做功,气体对外界所做的功W2 为负值。在两种情况下,气体都把热量传递给了汽缸,都属于放热,因此Q1、Q2 均为负值。
解:(1)压缩过程活塞对气体做的功W1= F1l1= 2 × 103×0.1 J= 200 J
气体内能的变化量ΔU1=W1+Q1=200J-25J=175J
(2)气体膨胀过程中气体对外界所做的功W2=F2l2=-9 × 103 × 0.1J=-900J
气体内能的变化量ΔU2= W2+ Q2=- 900J- 30J=- 930J
汽缸内气体在压缩过程中内能增加了175 J,在膨胀做功过程中气体内能减少了930 J。
1. 被压瘪但尚未破裂的乒乓球放在热水里泡一会儿,就会重新鼓起来,这一过程乒乓球内的气体( )
A. 吸热,对外做功,内能不变
B. 吸热,对外做功,内能增加
C. 温度升高,对外做功,内能不变
D. 压强增大,单位体积内分子数增大
B
2.根据热力学第一定律,下列说法正确的是( )
A. 电冰箱的工作过程表明,热量可以从低温物体向高温物体传递
B. 空调机在制冷过程中,从室内吸收的热量少于向室外放出的热量
C. 科技的进步可以使内燃机成为单一热源的热机
D. 对能源的过度消耗将使自然界的能量不断减少,形成能源危机
AAADFAAB
3.一定量的气体,从外界吸收热量2.7×105J,内能增加4.3×105J。在这一过程中,是气体对外做功,还是外界对气体做功?做了多少功?
Q=+2.7×105J
ΔU=+4.3×105J
﹀
ΔU=W + Q
得: W=1.6×105J >0
即外界对气体做功
解:
4.如图是用导热性能良好的材料制成的气体实验装置,开始时封闭的空气柱长度为20 cm,用竖直向下的力F压活塞,使空气柱长度变为原来的一半,人对活塞做功10 J,大气压强为p0=1×105 Pa,不计活塞的重力,求:
(1)若用足够长的时间缓慢压缩,压缩后气体的压强;
(2)若以适当的速度压缩气体,此过程气体向外散失的热量为2 J,则气体的内能增加多少?(活塞的横截面积S=1 cm2)
解:(1)设压缩后气体的压强为p,缓慢压缩,气体温度不变,由玻意耳定律:p0V0=pV
解得p=2×105 Pa。
(2)大气压力对活塞做功W1=p0SΔh=1 J,人对活塞做功W2=10 J,由热力学第一定律:ΔU=W1+W2+Q
将数据代入,解得ΔU=9 J。
热力学第一定律
热力学第一定律
表述:一个热力学系统的内能增量等于外界向它传递的热量与外界对它所做的功的和
数学表达式:ΔU= Q +W
定律中各量的正、负号及含义
热力学第一定律的应用
ΔU =0,则 W =- Q
W=0,则ΔU = Q
Q =0,则ΔU = W
热力学第一定律与理想气体状态方程结合问题的分析思路
同课章节目录
- 第一章 分子动理论
- 1 分子动理论的基本内容
- 2 实验:用油膜法估测油酸分子的大小
- 3 分子运动速率分布规律
- 4 分子动能和分子势能
- 第二章 气体、固体和液体
- 1 温度和温标
- 2 气体的等温变化
- 3 气体的等压变化和等容变化
- 4 固体
- 5 液体
- 第三章 热力学定律
- 1 功、热和内能的改变
- 2 热力学第一定律
- 3 能量守恒定律
- 4 热力学第二定律
- 第四章 原子结构和波粒二象性
- 1 普朗克黑体辐射理论
- 2 光电效应
- 3 原子的核式结构模型
- 4 氢原子光谱和玻尔的原子模型
- 5 粒子的波动性和量子力学的建立
- 第五章 原子核
- 1 原子核的组成
- 2 放射性元素的衰变
- 3 核力与结合能
- 4 核裂变与核聚变
- 5 “基本”粒子
