专项训练 线段和角的数学思想专练(含答案)
文档属性
| 名称 | 专项训练 线段和角的数学思想专练(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 4.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-08 22:06:14 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
专项训练
线段和角的数学思想专练
类型一 从特殊到一般思想
1.试验探索:过两点可以画一条直线,那么请在图中分别画线,并回答下列问题:
(1)图1中最多可以画几条直线
(2)图2中最多可以画几条直线
(3)图3中最多可以画几条直线
归纳结论:如果平面内有 个点,且每3个点均不在同一条直线上,那么最多可以画出几条直线 用含 n的代数式表示.
解决问题:某班50名同学在毕业后的一次聚会中,若每两人握一次手,则共握_________次手;若每两人要互赠礼物留念,则共需__________件礼物.
类型二 分类讨论思想
2.已知A,B,C 三点在同一条直线上,且线段 点M 为线段AB的中点,线段 点N 为线段 BC 的中点,求线段 MN 的长.
3.阅读材料,并回答问题:
材料:
数学课上,老师给出了如下问题:
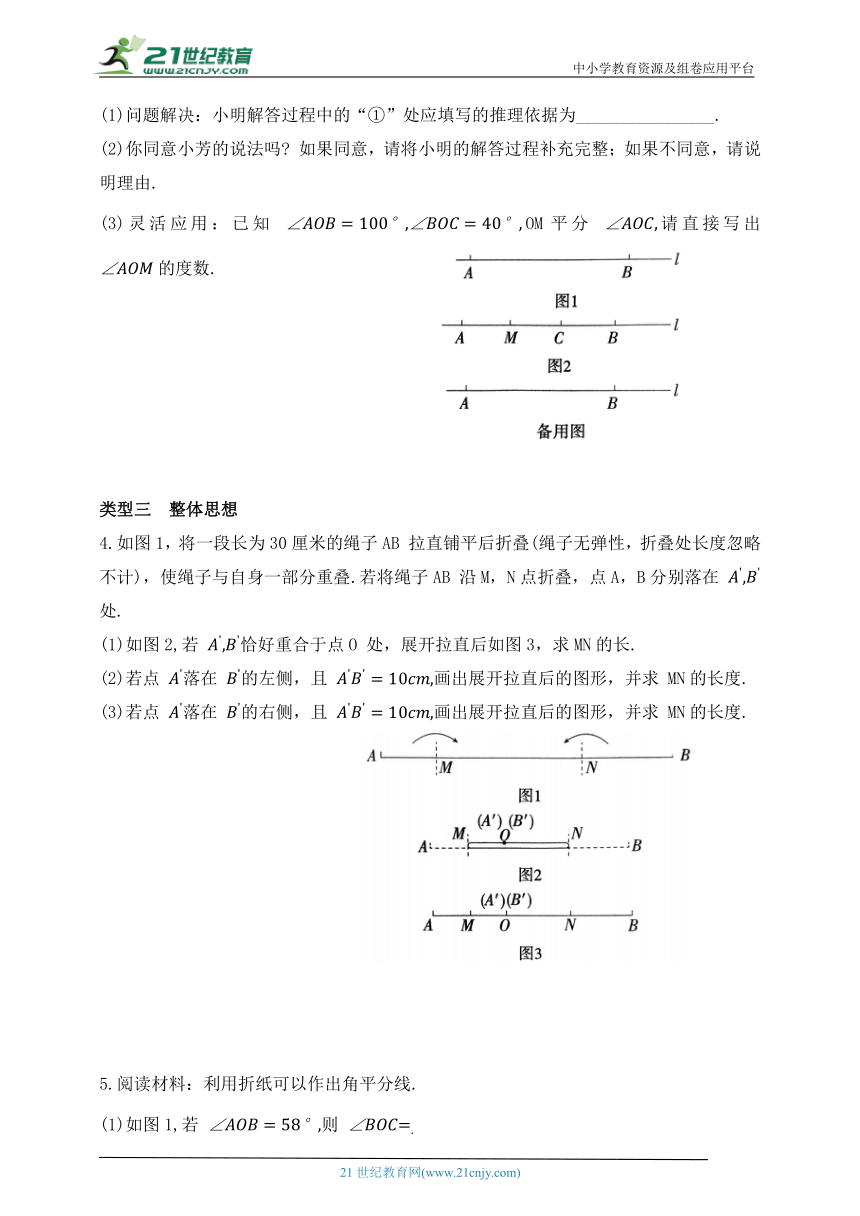
如图1,已知点A,B,C均在直线l上, M是AC的中点,求AM 的长.
小明的解答过程如下:
如图2,
又∵M是AC的中点,
小芳说:“小明的解答不完整.”
(1)问题解决:小明解答过程中的“①”处应填写的推理依据为________________.
(2)你同意小芳的说法吗 如果同意,请将小明的解答过程补充完整;如果不同意,请说明理由.
(3)灵活应用:已知 OM平分 请直接写出 的度数.
类型三 整体思想
4.如图1,将一段长为30厘米的绳子AB 拉直铺平后折叠(绳子无弹性,折叠处长度忽略不计),使绳子与自身一部分重叠.若将绳子AB 沿M,N点折叠,点A,B分别落在 处.
(1)如图2,若 恰好重合于点O 处,展开拉直后如图3,求MN的长.
(2)若点 落在 的左侧,且 画出展开拉直后的图形,并求 MN的长度.
(3)若点 落在 的右侧,且 画出展开拉直后的图形,并求 MN的长度.
5.阅读材料:利用折纸可以作出角平分线.
(1)如图1,若 则
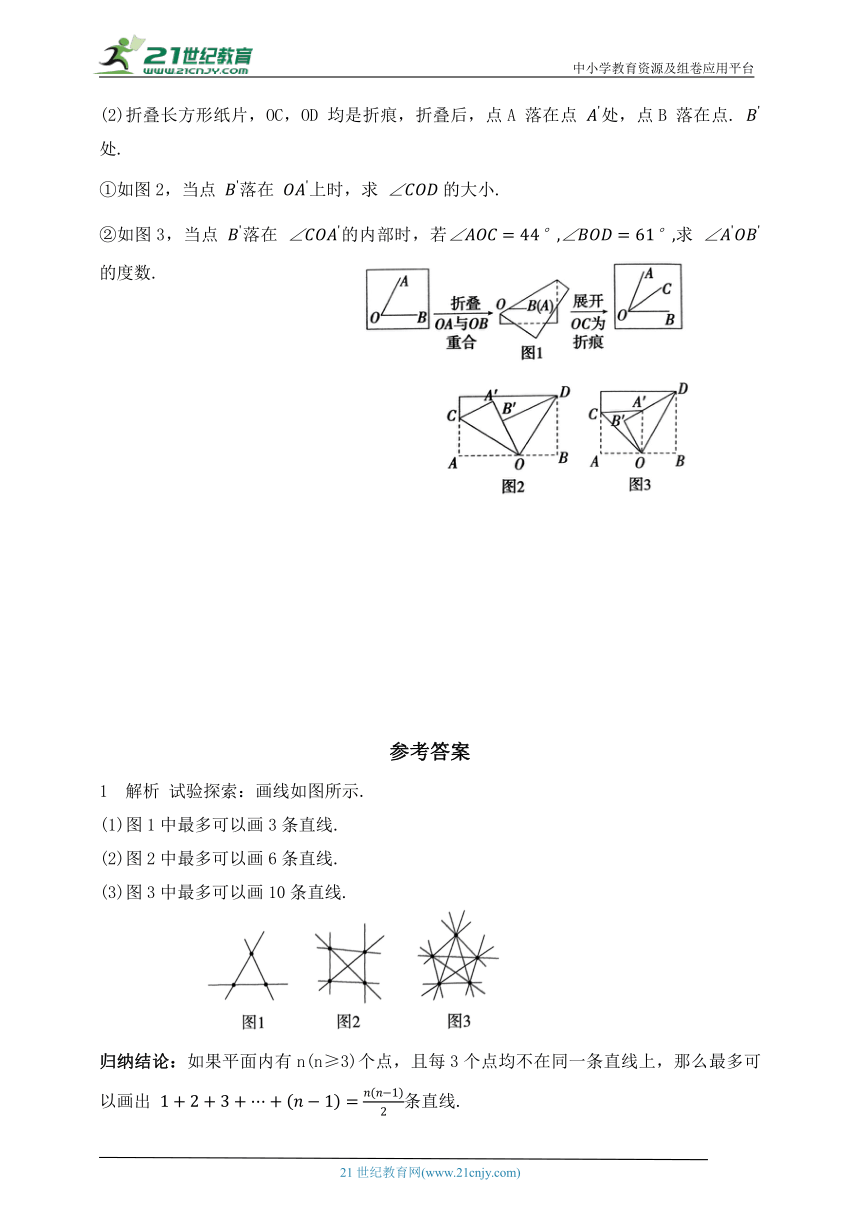
(2)折叠长方形纸片,OC,OD 均是折痕,折叠后,点A 落在点 处,点B 落在点. 处.
①如图2,当点 落在 上时,求 的大小.
②如图3,当点 落在 的内部时,若求 的度数.
参考答案
1 解析 试验探索:画线如图所示.
(1)图1中最多可以画3条直线.
(2)图2中最多可以画6条直线.
(3)图3中最多可以画10条直线.
归纳结论:如果平面内有n(n≥3)个点,且每3个点均不在同一条直线上,那么最多可以画出 条直线.
解决问题:某班50名同学在毕业后的一次聚会中,若每两人握一次手,则共握手 (次);若每两人要互赠礼物留念,则共需礼物 (50-1)=2450(件).
2 解析 ①当点 C 在线段AB上时,如图,
∵点 M 为线段AB的中点,点N为线段BC的中点,
∴MN=BM-BN=3cm.
②当点 C在线段AB 的延长线上时,如图,
易得
综上可知,线段 MN的长为3 cm或6 cm.
3 解析 (1)线段中点的定义.
(2)同意小芳的说法,补充小明的解答过程如下:
当点 C在点 B 右侧时,如图,
∵ M 是AC 的中点,
∴ AM 的长为4 或8.
(3)①当OC在 内部时,如图,
∵OM平分
②当OC在 外部时,如图,
∵ OM平分
综上所述,的度数为 或
4 解析 (1)∵将绳子AB沿 M,N点折叠,点A,B分别落在 处, 恰好重合于点 O 处,
(2)如图所示:
由题意得M,N分别为 的中点,
∴ MN=AB-(AM+BN)=30-10=20(cm).
(3)如图所示:
,
5 解析 (1)29°.
(2)①由折叠知 ∴ ∠AOA'=2∠AOC.
由折叠知∠BOD=∠B'OD,
∵点 落在 上,∴ ∠AOA'+∠BOB'=180°,
∴2∠AOC+2∠BOD=180°,∴ ∠AOC+∠BOD=90°,∴ ∠COD=90°.
②由折叠知∠AOA'=2∠AOC,∠BOB'=2∠BOD.
∵∠AOC=44°,∠BOD=61°,
∴ ∠AOA'=2∠AOC=2×44°=88°,∠BOB'=2∠BOD=2×61°=122°.
∵∠AOA'+∠BOB'-∠A'OB'=180°,
∴∠A'OB'=∠AOA'+∠BOB'-180°= 88°+122°-180°=30°.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
专项训练
线段和角的数学思想专练
类型一 从特殊到一般思想
1.试验探索:过两点可以画一条直线,那么请在图中分别画线,并回答下列问题:
(1)图1中最多可以画几条直线
(2)图2中最多可以画几条直线
(3)图3中最多可以画几条直线
归纳结论:如果平面内有 个点,且每3个点均不在同一条直线上,那么最多可以画出几条直线 用含 n的代数式表示.
解决问题:某班50名同学在毕业后的一次聚会中,若每两人握一次手,则共握_________次手;若每两人要互赠礼物留念,则共需__________件礼物.
类型二 分类讨论思想
2.已知A,B,C 三点在同一条直线上,且线段 点M 为线段AB的中点,线段 点N 为线段 BC 的中点,求线段 MN 的长.
3.阅读材料,并回答问题:
材料:
数学课上,老师给出了如下问题:
如图1,已知点A,B,C均在直线l上, M是AC的中点,求AM 的长.
小明的解答过程如下:
如图2,
又∵M是AC的中点,
小芳说:“小明的解答不完整.”
(1)问题解决:小明解答过程中的“①”处应填写的推理依据为________________.
(2)你同意小芳的说法吗 如果同意,请将小明的解答过程补充完整;如果不同意,请说明理由.
(3)灵活应用:已知 OM平分 请直接写出 的度数.
类型三 整体思想
4.如图1,将一段长为30厘米的绳子AB 拉直铺平后折叠(绳子无弹性,折叠处长度忽略不计),使绳子与自身一部分重叠.若将绳子AB 沿M,N点折叠,点A,B分别落在 处.
(1)如图2,若 恰好重合于点O 处,展开拉直后如图3,求MN的长.
(2)若点 落在 的左侧,且 画出展开拉直后的图形,并求 MN的长度.
(3)若点 落在 的右侧,且 画出展开拉直后的图形,并求 MN的长度.
5.阅读材料:利用折纸可以作出角平分线.
(1)如图1,若 则
(2)折叠长方形纸片,OC,OD 均是折痕,折叠后,点A 落在点 处,点B 落在点. 处.
①如图2,当点 落在 上时,求 的大小.
②如图3,当点 落在 的内部时,若求 的度数.
参考答案
1 解析 试验探索:画线如图所示.
(1)图1中最多可以画3条直线.
(2)图2中最多可以画6条直线.
(3)图3中最多可以画10条直线.
归纳结论:如果平面内有n(n≥3)个点,且每3个点均不在同一条直线上,那么最多可以画出 条直线.
解决问题:某班50名同学在毕业后的一次聚会中,若每两人握一次手,则共握手 (次);若每两人要互赠礼物留念,则共需礼物 (50-1)=2450(件).
2 解析 ①当点 C 在线段AB上时,如图,
∵点 M 为线段AB的中点,点N为线段BC的中点,
∴MN=BM-BN=3cm.
②当点 C在线段AB 的延长线上时,如图,
易得
综上可知,线段 MN的长为3 cm或6 cm.
3 解析 (1)线段中点的定义.
(2)同意小芳的说法,补充小明的解答过程如下:
当点 C在点 B 右侧时,如图,
∵ M 是AC 的中点,
∴ AM 的长为4 或8.
(3)①当OC在 内部时,如图,
∵OM平分
②当OC在 外部时,如图,
∵ OM平分
综上所述,的度数为 或
4 解析 (1)∵将绳子AB沿 M,N点折叠,点A,B分别落在 处, 恰好重合于点 O 处,
(2)如图所示:
由题意得M,N分别为 的中点,
∴ MN=AB-(AM+BN)=30-10=20(cm).
(3)如图所示:
,
5 解析 (1)29°.
(2)①由折叠知 ∴ ∠AOA'=2∠AOC.
由折叠知∠BOD=∠B'OD,
∵点 落在 上,∴ ∠AOA'+∠BOB'=180°,
∴2∠AOC+2∠BOD=180°,∴ ∠AOC+∠BOD=90°,∴ ∠COD=90°.
②由折叠知∠AOA'=2∠AOC,∠BOB'=2∠BOD.
∵∠AOC=44°,∠BOD=61°,
∴ ∠AOA'=2∠AOC=2×44°=88°,∠BOB'=2∠BOD=2×61°=122°.
∵∠AOA'+∠BOB'-∠A'OB'=180°,
∴∠A'OB'=∠AOA'+∠BOB'-180°= 88°+122°-180°=30°.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
