5.2统计的简单应用(第2课时)课件(共26张PPT)
文档属性
| 名称 | 5.2统计的简单应用(第2课时)课件(共26张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-04-15 18:09:22 | ||
图片预览





文档简介
课件26张PPT。5.2统计的简单
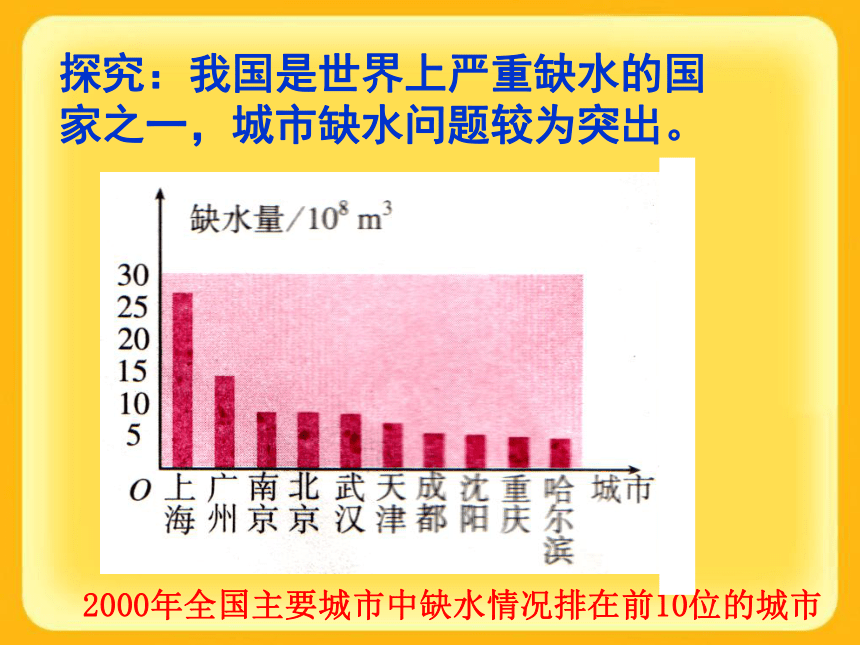
应用(2)2000年全国主要城市中缺水情况排在前10位的城市探究:我国是世界上严重缺水的国
家之一,城市缺水问题较为突出。 例 某市政府为了节约生活用水,计划在本市试行居民生活用水定额管理,即确定一个居民月用水量标准a ,用水量不超过a的部分按平价收费,超过a的部分按议价收费。 ①如果希望大部分居民的日常生活不受影响,那 么标准a定为多少比较合理呢? ②为了较合理地确定这个标准,你认为需要做
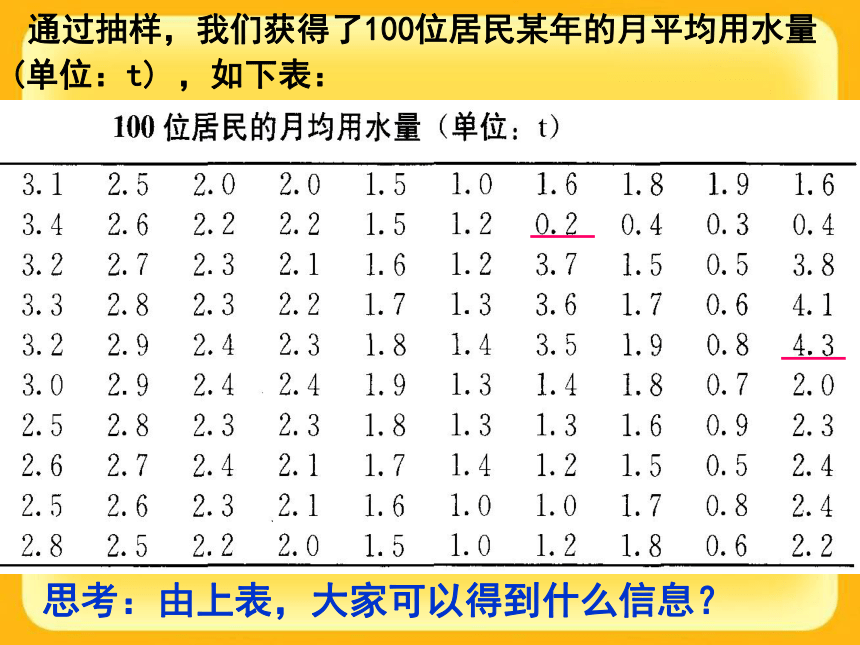
哪些工作? 思考:由上表,大家可以得到什么信息? 通过抽样,我们获得了100位居民某年的月平均用水量(单位:t) ,如下表: 1.求极差(即一组数据中最大值与最小值的差) 2.决定组距与组数组数= 4.3 - 0.2 = 4.13.将数据分组[0,0.5 ),[0.5,1 ),…,[4,4.5] 将一批数据按要求分为若干个组,各组内数据的个数,叫做该组的频数。
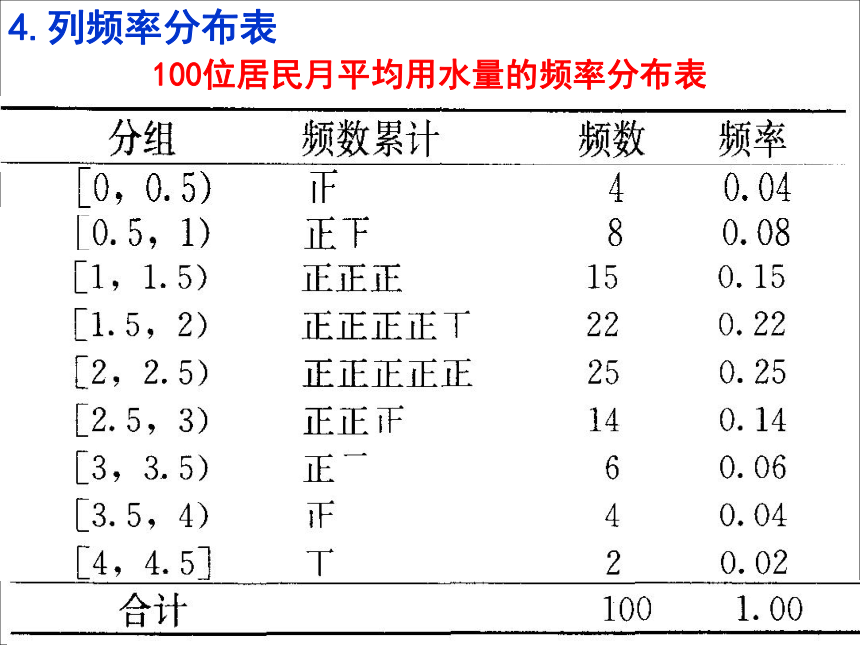
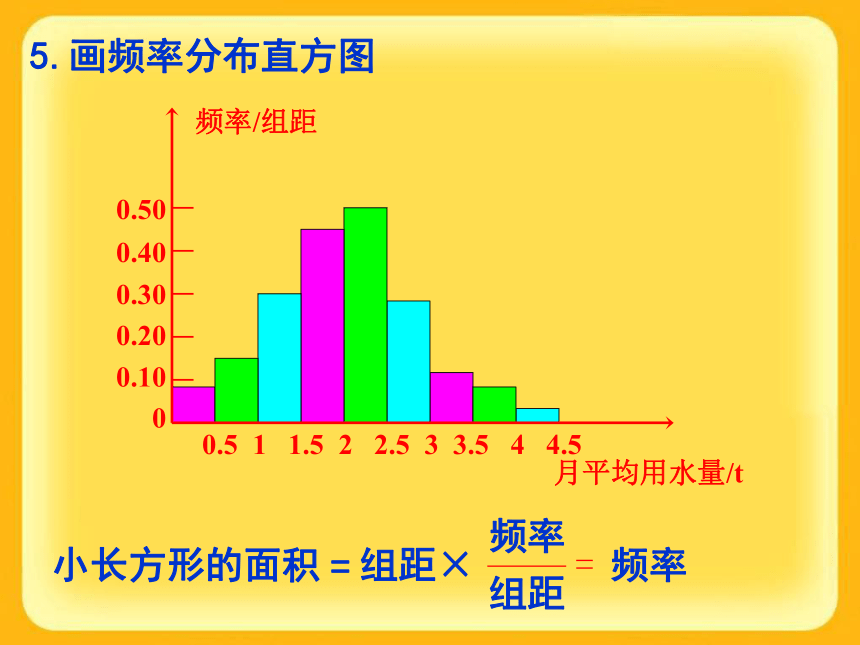
频率:每组数据的个数除以全体数据个数的商叫做该组的频率。4.列频率分布表100位居民月平均用水量的频率分布表5.画频率分布直方图小长方形的面积组距×频率=探究:
同样一组数据,如果组距不同,横轴、纵轴的单位不同,得到的图的形状也会不同。不同的形状给人以不同的印象,这种印象有时会影响我们对总体的判断。分别以1和0.1为组距重新作图,然后谈谈你对图的印象。 一、求极差,即数据中最大值与最小值的差二、决定组距与组数 :组距=极差/组数三、分组,通常对组内数值所在区间,
取左闭右开区间 , 最后一组取闭区间四、登记频数,计算频率,列出频率分布表画一组数据的频率分布直方图,可以按以下的步骤进行:五、画出频率分布直方图(纵轴表示频率/组距)如果当地政府希望85%以上的居民每月的用水量不超出标准,根据频率分布表和频率分布直方图,你能对制定月用水量提出建议吗?你认为3吨这个标准一定能够保证85%以上的居民用水量不超过标准吗?100位居民月平均用水量的频率分布表练 习1.有一个容量为50的样本数据的分组的频数如下:[12.5, 15.5) 3[15.5, 18.5) 8[18.5, 21.5) 9[21.5, 24.5) 11[24.5, 27.5) 10[27.5, 30.5) 5[30.5, 33.5) 4(1)列出样本的频率分布表;(2)画出频率分布直方图;(3)根据频率分布直方图估计,数据落在[15.5, 24.5)的百分比是多少? 解:组距为3 分组 频数 频率[12.5, 15.5) 3[15.5, 18.5) 8[18.5, 21.5) 9[21.5, 24.5) 11[24.5, 27.5) 10[27.5, 30.5) 5[30.5, 33.5) 40.06
0.16
0.18
0.22
0.20
0.10
0.080.020
0.053
0.060
0.073
0.067
0.033
0.027频率/ 组距合计 50 1频率分布直方图如下:频率/组距
0.0100.0200.0300.0400.05012.515.50.0600.070例2、为了了解一大片经济林的生长情况,随机测量其中的100株的底部周长,得到如下数据表(长度单位:cm): (1)编制频率分布表;(2)绘制频率分布直方图;
(3)估计该片经济林中底部周长小于100cm的树木约占多 少,周长不小于120cm的树木约占多少。解:
(1)从表中可以看出:
这组数据的最大值为135,最小值为80,
故极差为55,
可将其分为11组,组距为5。
从第1组[80,85)开始,
将各组的频数、频率和 频率/组距 填入表中例2、对某电子元件进行寿命跟踪调查,情况如下:
1)、列出频率分布表
2)、估计电子元件寿命在100h~400h以内的频率
3)、估计电子元件寿命在400h以上频率
课堂练习: 1、为检测某种产品的质量,抽取了一个容量为30的样本, 检测结果为一级品5件,二级品8件,三级品13件,次品4件.
(1) 列出样本的频率分布表;
(2)根据上述结果,估计此种产品为二级品或三级品的概率约是多少. (2)此种产品为二级品或三级品的概率约为0.27+0.43=0.7.
2.有一个容量为50的样本,数据的分组及其频数如下所示, 请将其制成频率直方图.
频率分布表如下:0.060.160.180.220.200.100.081.00频数3.已知样本10, 8, 6, 10, 8,13,11,10,12,7,8,9,12,9,
11,12,9,10,11,11, 那么频率为0.2范围的是 ( )A. 5.5~7.5 B. 7.5~9.5 C. 9.5~11.5 D. 11.5~13.5D4.一个容量为100的样本,数据的分组和各组的相关信息如下表,试完成表中每一行的两个空格.课堂小结编制频率分布直方图的步骤:①找最大值与最小值。②决定组距与组数③决定分点④登记频数,计算频率,列表,画直方图说明:(1)确定分点时,使分点比数据多一位小数,并且把第1小组的起点稍微再小一点.例:已知一个样本,填写下面的频率分布表
7.0 6.6 6.8 7.0 7.2 7.4 7.0 7.3 7.5 7.4
7.3 7.1 7.0 6.9 6.7 7.1 7.2 7.0 6.9 7.1
小结:思考 :
如果当地政府希望使 85% 以上的居民每月的用水量不超出标准,根据频率分布表和频率分布直方图,你能对制定月用水量标准提出建议吗? 频率分布直方图应用1.求极差2.决定组距与组数3.将数据分组4.列频率分布表5.画频率分布直方图
应用(2)2000年全国主要城市中缺水情况排在前10位的城市探究:我国是世界上严重缺水的国
家之一,城市缺水问题较为突出。 例 某市政府为了节约生活用水,计划在本市试行居民生活用水定额管理,即确定一个居民月用水量标准a ,用水量不超过a的部分按平价收费,超过a的部分按议价收费。 ①如果希望大部分居民的日常生活不受影响,那 么标准a定为多少比较合理呢? ②为了较合理地确定这个标准,你认为需要做
哪些工作? 思考:由上表,大家可以得到什么信息? 通过抽样,我们获得了100位居民某年的月平均用水量(单位:t) ,如下表: 1.求极差(即一组数据中最大值与最小值的差) 2.决定组距与组数组数= 4.3 - 0.2 = 4.13.将数据分组[0,0.5 ),[0.5,1 ),…,[4,4.5] 将一批数据按要求分为若干个组,各组内数据的个数,叫做该组的频数。
频率:每组数据的个数除以全体数据个数的商叫做该组的频率。4.列频率分布表100位居民月平均用水量的频率分布表5.画频率分布直方图小长方形的面积组距×频率=探究:
同样一组数据,如果组距不同,横轴、纵轴的单位不同,得到的图的形状也会不同。不同的形状给人以不同的印象,这种印象有时会影响我们对总体的判断。分别以1和0.1为组距重新作图,然后谈谈你对图的印象。 一、求极差,即数据中最大值与最小值的差二、决定组距与组数 :组距=极差/组数三、分组,通常对组内数值所在区间,
取左闭右开区间 , 最后一组取闭区间四、登记频数,计算频率,列出频率分布表画一组数据的频率分布直方图,可以按以下的步骤进行:五、画出频率分布直方图(纵轴表示频率/组距)如果当地政府希望85%以上的居民每月的用水量不超出标准,根据频率分布表和频率分布直方图,你能对制定月用水量提出建议吗?你认为3吨这个标准一定能够保证85%以上的居民用水量不超过标准吗?100位居民月平均用水量的频率分布表练 习1.有一个容量为50的样本数据的分组的频数如下:[12.5, 15.5) 3[15.5, 18.5) 8[18.5, 21.5) 9[21.5, 24.5) 11[24.5, 27.5) 10[27.5, 30.5) 5[30.5, 33.5) 4(1)列出样本的频率分布表;(2)画出频率分布直方图;(3)根据频率分布直方图估计,数据落在[15.5, 24.5)的百分比是多少? 解:组距为3 分组 频数 频率[12.5, 15.5) 3[15.5, 18.5) 8[18.5, 21.5) 9[21.5, 24.5) 11[24.5, 27.5) 10[27.5, 30.5) 5[30.5, 33.5) 40.06
0.16
0.18
0.22
0.20
0.10
0.080.020
0.053
0.060
0.073
0.067
0.033
0.027频率/ 组距合计 50 1频率分布直方图如下:频率/组距
0.0100.0200.0300.0400.05012.515.50.0600.070例2、为了了解一大片经济林的生长情况,随机测量其中的100株的底部周长,得到如下数据表(长度单位:cm): (1)编制频率分布表;(2)绘制频率分布直方图;
(3)估计该片经济林中底部周长小于100cm的树木约占多 少,周长不小于120cm的树木约占多少。解:
(1)从表中可以看出:
这组数据的最大值为135,最小值为80,
故极差为55,
可将其分为11组,组距为5。
从第1组[80,85)开始,
将各组的频数、频率和 频率/组距 填入表中例2、对某电子元件进行寿命跟踪调查,情况如下:
1)、列出频率分布表
2)、估计电子元件寿命在100h~400h以内的频率
3)、估计电子元件寿命在400h以上频率
课堂练习: 1、为检测某种产品的质量,抽取了一个容量为30的样本, 检测结果为一级品5件,二级品8件,三级品13件,次品4件.
(1) 列出样本的频率分布表;
(2)根据上述结果,估计此种产品为二级品或三级品的概率约是多少. (2)此种产品为二级品或三级品的概率约为0.27+0.43=0.7.
2.有一个容量为50的样本,数据的分组及其频数如下所示, 请将其制成频率直方图.
频率分布表如下:0.060.160.180.220.200.100.081.00频数3.已知样本10, 8, 6, 10, 8,13,11,10,12,7,8,9,12,9,
11,12,9,10,11,11, 那么频率为0.2范围的是 ( )A. 5.5~7.5 B. 7.5~9.5 C. 9.5~11.5 D. 11.5~13.5D4.一个容量为100的样本,数据的分组和各组的相关信息如下表,试完成表中每一行的两个空格.课堂小结编制频率分布直方图的步骤:①找最大值与最小值。②决定组距与组数③决定分点④登记频数,计算频率,列表,画直方图说明:(1)确定分点时,使分点比数据多一位小数,并且把第1小组的起点稍微再小一点.例:已知一个样本,填写下面的频率分布表
7.0 6.6 6.8 7.0 7.2 7.4 7.0 7.3 7.5 7.4
7.3 7.1 7.0 6.9 6.7 7.1 7.2 7.0 6.9 7.1
小结:思考 :
如果当地政府希望使 85% 以上的居民每月的用水量不超出标准,根据频率分布表和频率分布直方图,你能对制定月用水量标准提出建议吗? 频率分布直方图应用1.求极差2.决定组距与组数3.将数据分组4.列频率分布表5.画频率分布直方图
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
