北师大版数学(2024 )七年级下册第一次月考(培优)试题(含答案)
文档属性
| 名称 | 北师大版数学(2024 )七年级下册第一次月考(培优)试题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 112.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-09 06:17:35 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
北师大版数学(2024 )七年级下册第一次月考(培优)试题
一、单选题
1.(2023九下·昭平模拟)下列计算正确的是( )
A. B. C. D.
2.(2017·宁城模拟)下列运算的结果中,是正数的是( )
A.(﹣2007)﹣1 B.(﹣1)2007
C.(﹣1)×(﹣2007) D.(﹣2007)÷2007
3.计算14a6÷(-2a2)的结果是( )
A.-7a3 B.-7a4 C.7a3 D.7a4
4.计算a(-a3)·(a2)5的结果为( )
A.a14 B.-a14 C.a11 D.-a11
5.(2022七上·黄浦期中)现有下列算式:(1);(2);(3);(4);其中错误的有( )
A.1个 B.2个 C.3个 D.4个
6.(2023九上·淮安月考)斑叶兰被列为国家二级保护植物,它的一粒种子重约0.0000005克.将0.0000005用科学记数法表示为( )
A.5×107 B.5×10﹣7 C.0.5×10﹣6 D.5×10﹣6
7.(2023·海曙模拟)下列计算正确的是( )
A.(x2)3=x5 B.x2·x3=x6 C.x3+x3=2x3 D.x3÷x3=x
8.(2024八下·香洲期中) 将四个全等的直角三角形(直角边分别为、)按图1和图2两种方式放置,则能验证的等式是( )
A. B.
C. D.
9.(2024七下·宜兴期中)若二次三项式x2﹣mx+16是一个完全平方式,则字母m的值是( )
A.4 B.﹣4 C.±4 D.±8
10.(2022七上·济阳期末)(2+1)(22+1)(24+1)…(216+1)的结果为( )
A.232-1 B.232+1 C.232 D.216
二、填空题
11.(2022七下·杭州期中)新冠病毒的直径为125纳米,已知1纳米=0.000001毫米,125纳米用科学记数法表示为 米.
12.(2022八上·丰南期末)已知,,则的值为 .
13.(2024七上·浦东期中)若,则 .
14.(2022七下·银海期中)若a3m=4,则a9m= .
15.(2024八上·绿园月考)若的积中不含项,则 , .
16.(2024七下·九江)我国宋代数学家杨辉所著《详解九章算法》中记载了用如图所示的三角形解释了二项和的乘方展开式中的系数规律,我们把这种数字三角形叫做“杨辉三角”.请你利用杨辉三角,计算(a+b)6的展开式中,从左起第四项是 .
三、计算题
17.已知xa=2,xb=6.
(1)求xa﹣b的值.
(2)求x2a﹣b的值.
18.(2023八上·通榆月考)计算:(4a2-8a)÷2a
19.(2023七下·南县期中)使用整式乘法法则与公式可以使计算简便,请利用法则或公式计算下列各题
(1)已知,求的值
(2)计算:(写计算过程)
(3)设a,b,c,d都是正整数,并且,,求的值.
四、解答题
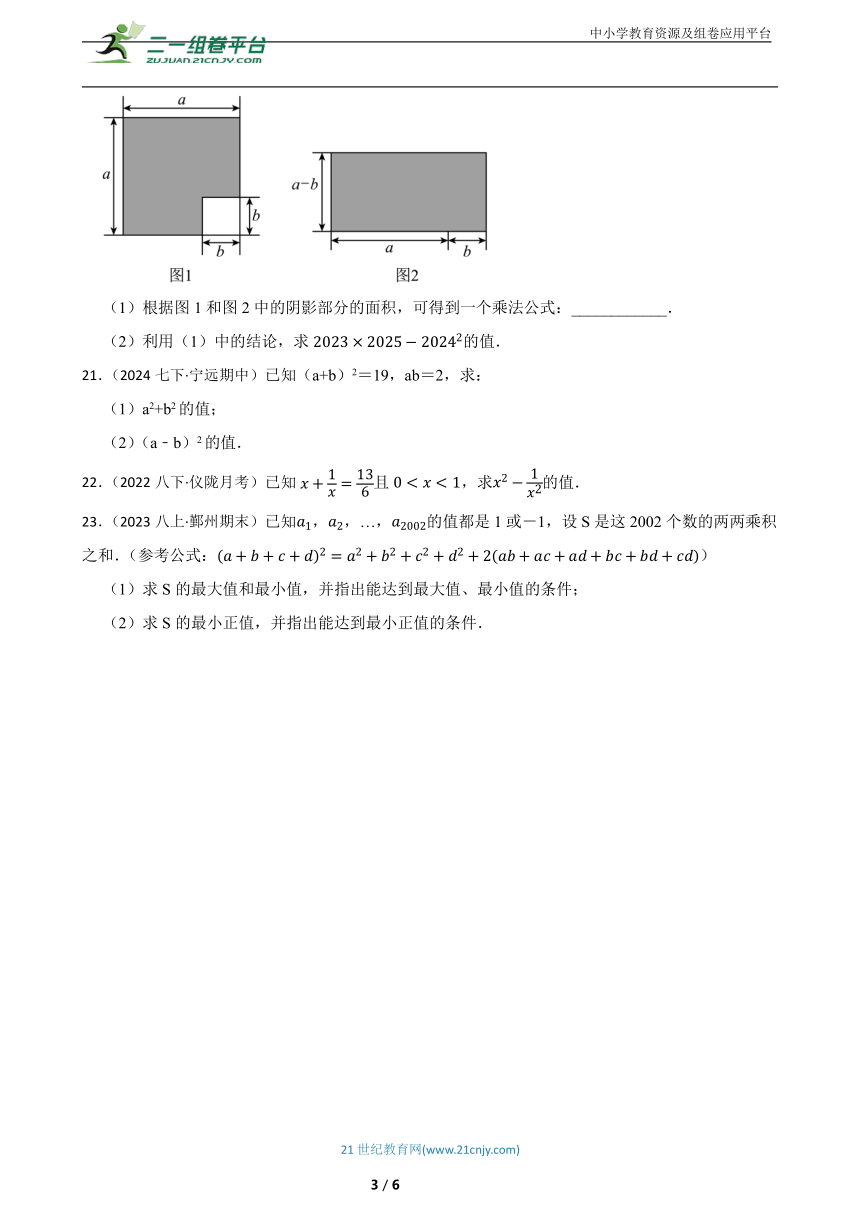
20.(2024七下·东台期中)图1是一张边长为a的正方形纸片,在它的一角剪去一个边长为b的小正方形,然后将图1剩余部分(阴影部分)剪拼成如图2所示的一个大长方形(阴影部分).
(1)根据图1和图2中的阴影部分的面积,可得到一个乘法公式:____________.
(2)利用(1)中的结论,求的值.
21.(2024七下·宁远期中)已知(a+b)2=19,ab=2,求:
(1)a2+b2的值;
(2)(a﹣b)2的值.
22.(2022八下·仪陇月考)已知且,求的值.
23.(2023八上·鄞州期末)已知,,…,的值都是1或-1,设S是这2002个数的两两乘积之和.(参考公式:)
(1)求S的最大值和最小值,并指出能达到最大值、最小值的条件;
(2)求S的最小正值,并指出能达到最小正值的条件.
答案解析部分
1.【答案】D
【知识点】同底数幂的乘法;零指数幂;合并同类项法则及应用;幂的乘方运算
2.【答案】C
【知识点】负整数指数幂;有理数的乘法法则;有理数的除法法则
3.【答案】B
【知识点】单项式除以单项式
4.【答案】B
【知识点】同底数幂的乘法;幂的乘方运算
5.【答案】C
【知识点】单项式乘单项式;合并同类项法则及应用;积的乘方运算;幂的乘方运算
6.【答案】B
【知识点】科学记数法表示大于0且小于1的数
7.【答案】C
【知识点】同底数幂的乘法;同底数幂的除法;合并同类项法则及应用;幂的乘方运算
8.【答案】D
【知识点】完全平方公式的几何背景
9.【答案】D
【知识点】平方差公式及应用
10.【答案】A
【知识点】平方差公式及应用
11.【答案】
【知识点】科学记数法表示大于0且小于1的数
12.【答案】
【知识点】同底数幂的除法;幂的乘方运算
13.【答案】
【知识点】同底数幂的乘法
14.【答案】64
【知识点】幂的乘方运算
15.【答案】3;9
【知识点】多项式乘多项式
16.【答案】20a3b3
【知识点】多项式乘多项式
17.【答案】(1)解:∵xa=2,xb=6,
∴xa﹣b=xa÷xb=2÷6=
(2)解:∵xa=2,xb=6,
∴x2a﹣b=(xa)2÷xb=22÷6=
【知识点】同底数幂的除法;幂的乘方运算
18.【答案】解:原式= (4a2-8a)÷2a
=4a2÷2a-8a÷2a
=2a-4.
【知识点】同底数幂的除法;多项式除以单项式
19.【答案】(1)
(2)6
(3)
【知识点】完全平方公式及运用;平方差公式及应用;有理数的乘方法则;有理数混合运算法则(含乘方)
20.【答案】(1)
(2)
【知识点】平方差公式的几何背景
21.【答案】(1)15;
(2)11
【知识点】完全平方公式及运用
22.【答案】解:∵,
∴,
∵,
∴,
∴,
∴.
【知识点】完全平方公式及运用;平方差公式及应用
23.【答案】(1)解:,
,
当或时,S取得最大值2003001;
当,,…,中有1001个1,1001个0时,S取得最小值.
(2)∵大于2002的最小完全平方数为,且必为偶数,
∴当或时,即当这2002个数中有1024个1,978个,或有1024个, 978个1时,S取得最小值.
【知识点】多项式乘多项式
21世纪教育网(www.21cnjy.com)
1 / 6
北师大版数学(2024 )七年级下册第一次月考(培优)试题
一、单选题
1.(2023九下·昭平模拟)下列计算正确的是( )
A. B. C. D.
2.(2017·宁城模拟)下列运算的结果中,是正数的是( )
A.(﹣2007)﹣1 B.(﹣1)2007
C.(﹣1)×(﹣2007) D.(﹣2007)÷2007
3.计算14a6÷(-2a2)的结果是( )
A.-7a3 B.-7a4 C.7a3 D.7a4
4.计算a(-a3)·(a2)5的结果为( )
A.a14 B.-a14 C.a11 D.-a11
5.(2022七上·黄浦期中)现有下列算式:(1);(2);(3);(4);其中错误的有( )
A.1个 B.2个 C.3个 D.4个
6.(2023九上·淮安月考)斑叶兰被列为国家二级保护植物,它的一粒种子重约0.0000005克.将0.0000005用科学记数法表示为( )
A.5×107 B.5×10﹣7 C.0.5×10﹣6 D.5×10﹣6
7.(2023·海曙模拟)下列计算正确的是( )
A.(x2)3=x5 B.x2·x3=x6 C.x3+x3=2x3 D.x3÷x3=x
8.(2024八下·香洲期中) 将四个全等的直角三角形(直角边分别为、)按图1和图2两种方式放置,则能验证的等式是( )
A. B.
C. D.
9.(2024七下·宜兴期中)若二次三项式x2﹣mx+16是一个完全平方式,则字母m的值是( )
A.4 B.﹣4 C.±4 D.±8
10.(2022七上·济阳期末)(2+1)(22+1)(24+1)…(216+1)的结果为( )
A.232-1 B.232+1 C.232 D.216
二、填空题
11.(2022七下·杭州期中)新冠病毒的直径为125纳米,已知1纳米=0.000001毫米,125纳米用科学记数法表示为 米.
12.(2022八上·丰南期末)已知,,则的值为 .
13.(2024七上·浦东期中)若,则 .
14.(2022七下·银海期中)若a3m=4,则a9m= .
15.(2024八上·绿园月考)若的积中不含项,则 , .
16.(2024七下·九江)我国宋代数学家杨辉所著《详解九章算法》中记载了用如图所示的三角形解释了二项和的乘方展开式中的系数规律,我们把这种数字三角形叫做“杨辉三角”.请你利用杨辉三角,计算(a+b)6的展开式中,从左起第四项是 .
三、计算题
17.已知xa=2,xb=6.
(1)求xa﹣b的值.
(2)求x2a﹣b的值.
18.(2023八上·通榆月考)计算:(4a2-8a)÷2a
19.(2023七下·南县期中)使用整式乘法法则与公式可以使计算简便,请利用法则或公式计算下列各题
(1)已知,求的值
(2)计算:(写计算过程)
(3)设a,b,c,d都是正整数,并且,,求的值.
四、解答题
20.(2024七下·东台期中)图1是一张边长为a的正方形纸片,在它的一角剪去一个边长为b的小正方形,然后将图1剩余部分(阴影部分)剪拼成如图2所示的一个大长方形(阴影部分).
(1)根据图1和图2中的阴影部分的面积,可得到一个乘法公式:____________.
(2)利用(1)中的结论,求的值.
21.(2024七下·宁远期中)已知(a+b)2=19,ab=2,求:
(1)a2+b2的值;
(2)(a﹣b)2的值.
22.(2022八下·仪陇月考)已知且,求的值.
23.(2023八上·鄞州期末)已知,,…,的值都是1或-1,设S是这2002个数的两两乘积之和.(参考公式:)
(1)求S的最大值和最小值,并指出能达到最大值、最小值的条件;
(2)求S的最小正值,并指出能达到最小正值的条件.
答案解析部分
1.【答案】D
【知识点】同底数幂的乘法;零指数幂;合并同类项法则及应用;幂的乘方运算
2.【答案】C
【知识点】负整数指数幂;有理数的乘法法则;有理数的除法法则
3.【答案】B
【知识点】单项式除以单项式
4.【答案】B
【知识点】同底数幂的乘法;幂的乘方运算
5.【答案】C
【知识点】单项式乘单项式;合并同类项法则及应用;积的乘方运算;幂的乘方运算
6.【答案】B
【知识点】科学记数法表示大于0且小于1的数
7.【答案】C
【知识点】同底数幂的乘法;同底数幂的除法;合并同类项法则及应用;幂的乘方运算
8.【答案】D
【知识点】完全平方公式的几何背景
9.【答案】D
【知识点】平方差公式及应用
10.【答案】A
【知识点】平方差公式及应用
11.【答案】
【知识点】科学记数法表示大于0且小于1的数
12.【答案】
【知识点】同底数幂的除法;幂的乘方运算
13.【答案】
【知识点】同底数幂的乘法
14.【答案】64
【知识点】幂的乘方运算
15.【答案】3;9
【知识点】多项式乘多项式
16.【答案】20a3b3
【知识点】多项式乘多项式
17.【答案】(1)解:∵xa=2,xb=6,
∴xa﹣b=xa÷xb=2÷6=
(2)解:∵xa=2,xb=6,
∴x2a﹣b=(xa)2÷xb=22÷6=
【知识点】同底数幂的除法;幂的乘方运算
18.【答案】解:原式= (4a2-8a)÷2a
=4a2÷2a-8a÷2a
=2a-4.
【知识点】同底数幂的除法;多项式除以单项式
19.【答案】(1)
(2)6
(3)
【知识点】完全平方公式及运用;平方差公式及应用;有理数的乘方法则;有理数混合运算法则(含乘方)
20.【答案】(1)
(2)
【知识点】平方差公式的几何背景
21.【答案】(1)15;
(2)11
【知识点】完全平方公式及运用
22.【答案】解:∵,
∴,
∵,
∴,
∴,
∴.
【知识点】完全平方公式及运用;平方差公式及应用
23.【答案】(1)解:,
,
当或时,S取得最大值2003001;
当,,…,中有1001个1,1001个0时,S取得最小值.
(2)∵大于2002的最小完全平方数为,且必为偶数,
∴当或时,即当这2002个数中有1024个1,978个,或有1024个, 978个1时,S取得最小值.
【知识点】多项式乘多项式
21世纪教育网(www.21cnjy.com)
1 / 6
同课章节目录
