人教版(2024)八年级上册 13.3.2等边三角形 学案(无答案)
文档属性
| 名称 | 人教版(2024)八年级上册 13.3.2等边三角形 学案(无答案) |  | |
| 格式 | doc | ||
| 文件大小 | 334.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-10 09:49:03 | ||
图片预览

文档简介
第13章 轴对称
13.3.2等边三角形
【学习目标】
1.探索并证明含30°锐角的直角三角形的性质.
2.能运用含30°角的直角三角形的性质解决简单的实际问题.
【学习重难点】
探索并证明含30°锐角的直角三角形的性质.
【教学过程】
预习
【温故习新】
新课导入:如图是屋架设计图的一部分,点 D 是斜梁 AB 的中点,立柱 BC,DE 垂直于横梁 AC,AB = 7.4 m,∠A = 30°,立柱 BC,DE 的长是多少?
知识点:含 30° 角的直角三角形的性质
活动一 剪一张等边三角形纸片,沿一边上的高对折,如图所示,你有什么发现?
活动二 剪下这个直角三角形,探究它的性质.
追问:你能类比探究等边三角形的性质探究它吗?
动手实践:在 Rt△ABC 中,已知 ∠C = 90°,∠A = 30°.证明:BC = AB.
含30°的直角三角形的性质定理:
在直角三角形中,如果有一个锐角是30°,那么它所对的直角边等于斜边的一半.
这个定理的前提条件是“在直角三角形中”,是证明直角三角形中一边等于另一边(斜边)的一半的重要方法之一,通常用于证明边的倍数关系.
【研讨拓展】
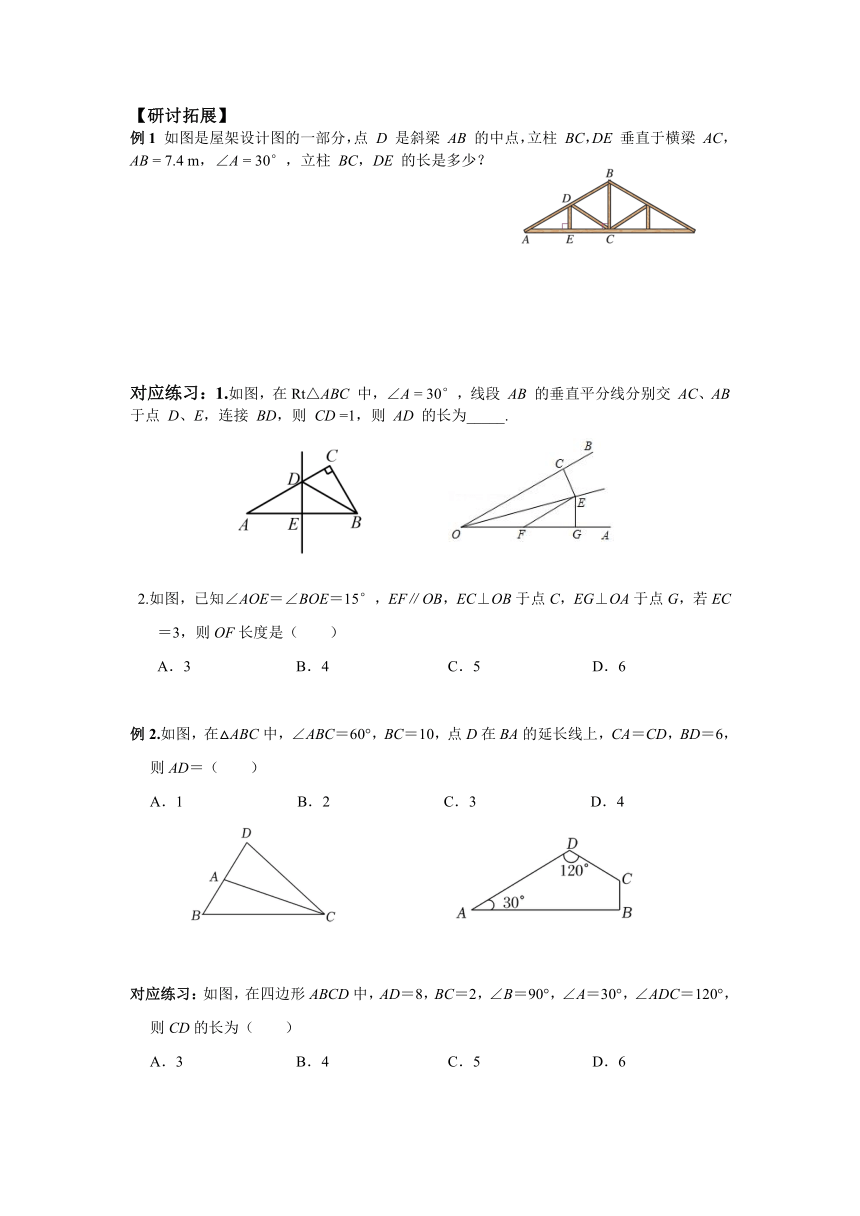
例1 如图是屋架设计图的一部分,点 D 是斜梁 AB 的中点,立柱 BC,DE 垂直于横梁 AC,AB = 7.4 m,∠A = 30°,立柱 BC,DE 的长是多少?
对应练习:1.如图,在Rt△ABC 中,∠A = 30°,线段 AB 的垂直平分线分别交 AC、AB 于点 D、E,连接 BD,则 CD =1,则 AD 的长为_____.
2.如图,已知∠AOE=∠BOE=15°,EF∥OB,EC⊥OB于点C,EG⊥OA于点G,若EC=3,则OF长度是( )
A.3 B.4 C.5 D.6
例2.如图,在△ABC中,∠ABC=60°,BC=10,点D在BA的延长线上,CA=CD,BD=6,则AD=( )
A.1 B.2 C.3 D.4
对应练习:如图,在四边形ABCD中,AD=8,BC=2,∠B=90°,∠A=30°,∠ADC=120°,则CD的长为( )
A.3 B.4 C.5 D.6
例3如图所示,为了躲避海盗,一轮船由西向东航行,早上8点,在A处测得小岛P在北偏东75°的方向上,以每小时20海里的速度继续向东航行,10点到达B处,并测得小岛P在北偏东60°的方向上,已知小岛周围22海里内有暗礁,若轮船仍向前航行,有无触礁的危险?
【反馈提炼】
如图,在Rt△ABC 中,∠ACB = 90°,∠A = 60°,AC =2cm,CD⊥AB,垂足为 D,那么 ∠ACD = _____°,AD = cm,AB = ___cm.
2.如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,∠A=60°,AD=2,则BD=( )
A.2 B.4 C.6 D.8
3.如图,△ABC是等边三角形,点D是BC边上任意一点,DE⊥AB于点E,DF⊥AC于点F.若BC=4,则BE+CF= .
4.如图,∠BAD = ∠DCB = 90°,AD = CB,AB = 3cm,∠2 = 15°.
(1) 求证△BED 是等腰三角形;
(2) 求△BED 的面积.
5.如图,在等边三角形 ABC 中,点 D、E 分别在边 AC、BC 上,将 △CED 沿着 DE 折叠,使点 C 落在边 AB 上的点 F 处,且 DF⊥AB,求证:BF = 2BE.
6 .如图,一条船上午8时从海岛A出发,以15海里/时的速度向正北方向航行,上午10时到达海岛B处,分别从A,B处望灯塔C,测得∠NAC=30°,∠NBC=60°.
(1)求海岛B到灯塔C的距离;
(2)若这条船继续向正北航行,问什么时间小船与灯塔C的距离最短?
【课堂小结】
本节课的思维导图:
(学生根据自己的理解和掌握情况自己绘制)
13.3.2等边三角形
【学习目标】
1.探索并证明含30°锐角的直角三角形的性质.
2.能运用含30°角的直角三角形的性质解决简单的实际问题.
【学习重难点】
探索并证明含30°锐角的直角三角形的性质.
【教学过程】
预习
【温故习新】
新课导入:如图是屋架设计图的一部分,点 D 是斜梁 AB 的中点,立柱 BC,DE 垂直于横梁 AC,AB = 7.4 m,∠A = 30°,立柱 BC,DE 的长是多少?
知识点:含 30° 角的直角三角形的性质
活动一 剪一张等边三角形纸片,沿一边上的高对折,如图所示,你有什么发现?
活动二 剪下这个直角三角形,探究它的性质.
追问:你能类比探究等边三角形的性质探究它吗?
动手实践:在 Rt△ABC 中,已知 ∠C = 90°,∠A = 30°.证明:BC = AB.
含30°的直角三角形的性质定理:
在直角三角形中,如果有一个锐角是30°,那么它所对的直角边等于斜边的一半.
这个定理的前提条件是“在直角三角形中”,是证明直角三角形中一边等于另一边(斜边)的一半的重要方法之一,通常用于证明边的倍数关系.
【研讨拓展】
例1 如图是屋架设计图的一部分,点 D 是斜梁 AB 的中点,立柱 BC,DE 垂直于横梁 AC,AB = 7.4 m,∠A = 30°,立柱 BC,DE 的长是多少?
对应练习:1.如图,在Rt△ABC 中,∠A = 30°,线段 AB 的垂直平分线分别交 AC、AB 于点 D、E,连接 BD,则 CD =1,则 AD 的长为_____.
2.如图,已知∠AOE=∠BOE=15°,EF∥OB,EC⊥OB于点C,EG⊥OA于点G,若EC=3,则OF长度是( )
A.3 B.4 C.5 D.6
例2.如图,在△ABC中,∠ABC=60°,BC=10,点D在BA的延长线上,CA=CD,BD=6,则AD=( )
A.1 B.2 C.3 D.4
对应练习:如图,在四边形ABCD中,AD=8,BC=2,∠B=90°,∠A=30°,∠ADC=120°,则CD的长为( )
A.3 B.4 C.5 D.6
例3如图所示,为了躲避海盗,一轮船由西向东航行,早上8点,在A处测得小岛P在北偏东75°的方向上,以每小时20海里的速度继续向东航行,10点到达B处,并测得小岛P在北偏东60°的方向上,已知小岛周围22海里内有暗礁,若轮船仍向前航行,有无触礁的危险?
【反馈提炼】
如图,在Rt△ABC 中,∠ACB = 90°,∠A = 60°,AC =2cm,CD⊥AB,垂足为 D,那么 ∠ACD = _____°,AD = cm,AB = ___cm.
2.如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,∠A=60°,AD=2,则BD=( )
A.2 B.4 C.6 D.8
3.如图,△ABC是等边三角形,点D是BC边上任意一点,DE⊥AB于点E,DF⊥AC于点F.若BC=4,则BE+CF= .
4.如图,∠BAD = ∠DCB = 90°,AD = CB,AB = 3cm,∠2 = 15°.
(1) 求证△BED 是等腰三角形;
(2) 求△BED 的面积.
5.如图,在等边三角形 ABC 中,点 D、E 分别在边 AC、BC 上,将 △CED 沿着 DE 折叠,使点 C 落在边 AB 上的点 F 处,且 DF⊥AB,求证:BF = 2BE.
6 .如图,一条船上午8时从海岛A出发,以15海里/时的速度向正北方向航行,上午10时到达海岛B处,分别从A,B处望灯塔C,测得∠NAC=30°,∠NBC=60°.
(1)求海岛B到灯塔C的距离;
(2)若这条船继续向正北航行,问什么时间小船与灯塔C的距离最短?
【课堂小结】
本节课的思维导图:
(学生根据自己的理解和掌握情况自己绘制)
