【核心素养】2.1 运动的合成与分解 教案
文档属性
| 名称 | 【核心素养】2.1 运动的合成与分解 教案 |

|
|
| 格式 | docx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁科版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2025-01-09 00:00:00 | ||
图片预览



文档简介
2.1 运动的合成与分解 教案
【教材分析】
本节是以后抛体运动、圆周运动的基础,是学好以后知识的基本保证。通过学生举例、图片观察,分析运动特点,猜想曲线运动的方向,之后通过实验验证学生关于曲线运动的速度方向的猜想,并从理论上分析出曲线运动的方向。对于物体做直线运动和曲线运动的条件,首先让学生猜想,然后用实验验证,根据学生实际情况,依据牛顿定律:力、加速度、速度的关系,得出物体做曲线运动的条件。通过小船过河总结出运动的合成与分解的规律。并且运用运动的合成与分解的规律来解决小船渡河等实际问题。
【教学目标与核心素养】
物理观念:能了解曲线运动的内涵,知道物体做曲线运动的条件,掌握运动的合成与分解的规律,并且运用运动的合成与分解的规律来解决小船渡河等实际问题,形成运动的合成与分解的观念。
科学思维:通过探究的过程,让学生体会得到能体会将复杂运动分解为简单运动的物理思想. 科学探究:通过实验探究过程组织学生总结出曲线运动的速度方向;并给予理论证明。
科学态度与责任:能领略曲线运动的奇妙与和谐,发展对科学的好奇心与求知欲。
【教学重难点】
1.重点:理解曲线运动是变速运动,判定物体做曲线运动的方向以及明确物体做曲线运动的条件,并且掌握运动合成与分解的方法。
2.难点:理解合运动和它的分运动是等效替代的关系并且运用运动的合成与分解的规律来解决小船渡河等实际问题。
【教学过程】
【新课导入】
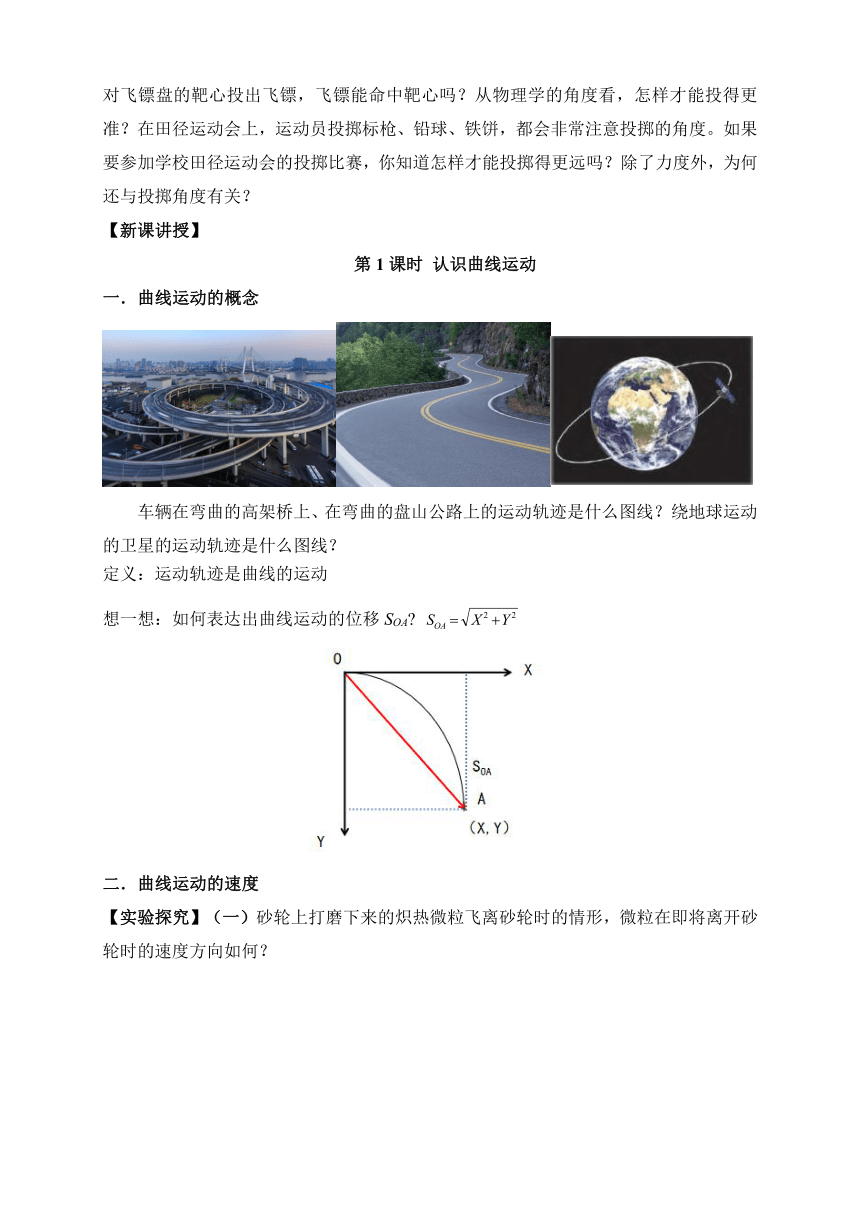
飞镖运动是一项非常有趣的运动。在一次飞镖比赛中,一位同学沿水平方向正对飞镖盘的靶心投出飞镖,飞镖能命中靶心吗?从物理学的角度看,怎样才能投得更准?在田径运动会上,运动员投掷标枪、铅球、铁饼,都会非常注意投掷的角度。如果要参加学校田径运动会的投掷比赛,你知道怎样才能投掷得更远吗?除了力度外,为何还与投掷角度有关?
【新课讲授】
认识曲线运动
一.曲线运动的概念
车辆在弯曲的高架桥上、在弯曲的盘山公路上的运动轨迹是什么图线?绕地球运动的卫星的运动轨迹是什么图线?
定义:运动轨迹是曲线的运动
想一想:如何表达出曲线运动的位移SOA
二.曲线运动的速度
【实验探究】(一)砂轮上打磨下来的炽热微粒飞离砂轮时的情形,微粒在即将离开砂轮时的速度方向如何?
答:火星由于惯性,以脱离砂轮时的速度沿切线方向飞出,切线方向即为火星飞出时的速度方向。
(二)雨滴飞离雨伞时的情形,雨滴在即将离开雨伞时的速度方向如何?
答:水滴沿伞边缘的切线方向飞出。
【实验分析】1、砂轮边缘的沙粒的运动轨迹是什么?火星飞出方向是怎样的
答:砂轮边缘的沙粒的轨迹是个圆,火星从砂轮边缘的切线方向飞出。
水滴运动的轨迹是什么?飞出方向是怎样的
答:水滴随雨伞一起转动,它的轨迹是个圆,水滴从雨伞边缘的切线方向飞出
【实验结论】做曲线运动物体的速度方向是曲线上的某一点切线方向
【理论分析】
瞬时速度
当时间Δt或位移Δx趋近于零时:
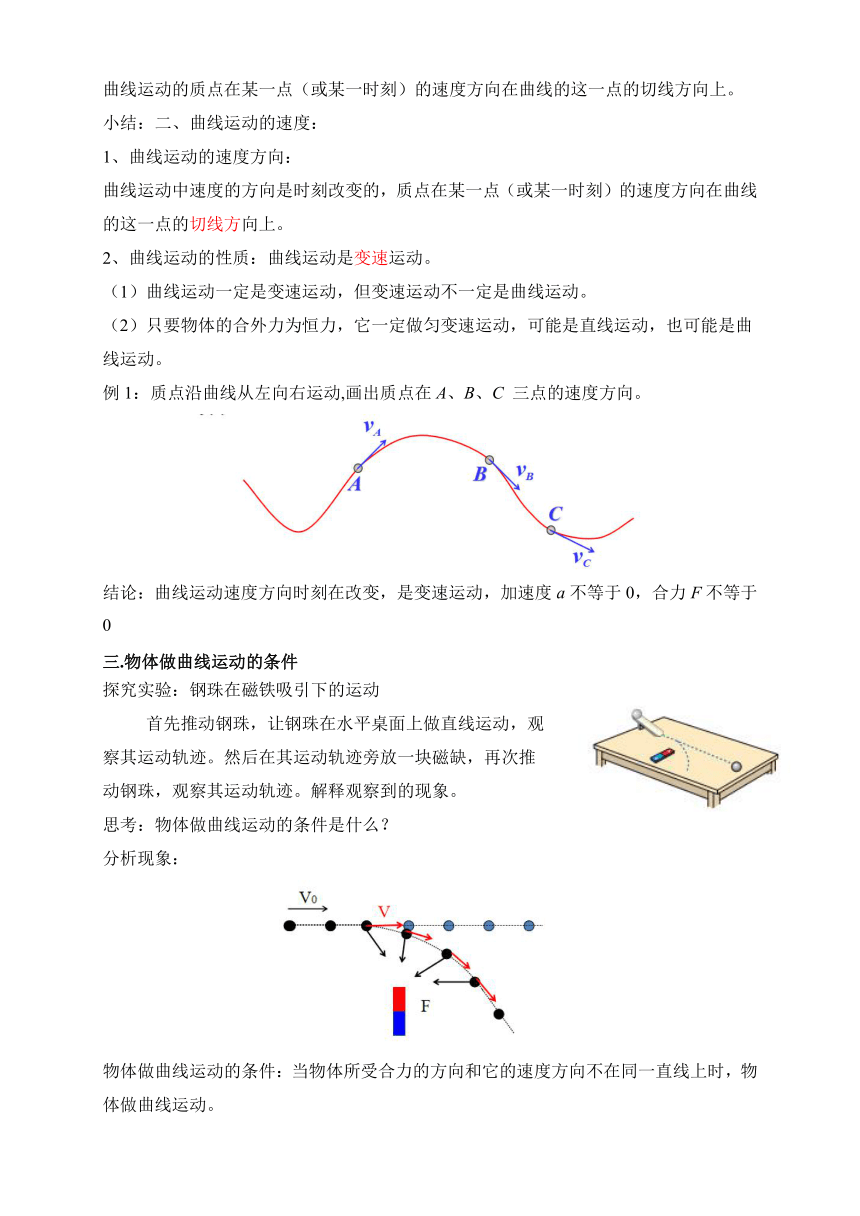
曲线运动的质点在某一点(或某一时刻)的速度方向在曲线的这一点的切线方向上。
小结:二、曲线运动的速度:
1、曲线运动的速度方向:
曲线运动中速度的方向是时刻改变的,质点在某一点(或某一时刻)的速度方向在曲线的这一点的切线方向上。
曲线运动的性质:曲线运动是变速运动。
(1)曲线运动一定是变速运动,但变速运动不一定是曲线运动。
(2)只要物体的合外力为恒力,它一定做匀变速运动,可能是直线运动,也可能是曲线运动。
例1:质点沿曲线从左向右运动,画出质点在A、B、C 三点的速度方向。
结论:曲线运动速度方向时刻在改变,是变速运动,加速度a不等于0,合力F不等于0
三.物体做曲线运动的条件
探究实验:钢珠在磁铁吸引下的运动
首先推动钢珠,让钢珠在水平桌面上做直线运动,观察其运动轨迹。然后在其运动轨迹旁放一块磁缺,再次推动钢珠,观察其运动轨迹。解释观察到的现象。
思考:物体做曲线运动的条件是什么?
分析现象:
物体做曲线运动的条件:当物体所受合力的方向和它的速度方向不在同一直线上时,物体做曲线运动。
思考:
做曲线运动的物体运动轨迹、速度方向与其所受合外力方向三者 位置关系如何?
答:物体运动轨迹夹在速度方向和合外力方向之间。
2.做曲线运动的物体运动轨迹弯曲方向与其所受合外力方向有什么关系呢?
答:做曲线运动的物体所受合外力必指向运动轨迹凹的一侧
结论:曲线运动轨迹始终夹在合外力方向与速度方向之间,合外力指向轨迹内侧。
总结:F、a、v三者关系辨析
F合(a) 跟 v 在同一直线上 直线运动
F合(a) 恒定→匀变速直线运动
F合(a) 变化→变加速直线运动
F合(a) 跟 v 不在同一直线上 曲线运动
F合(a) 恒定→匀变速曲线运动
F合(a) 变化→变加速曲线运动
说明:判断直线还是曲线运动关键看a 与v 是否同一直线;判断匀变速还是变加速关键看a 是否恒定
例2.(多选)关于曲线运动,下列说法正确的是【 AC 】
A.做曲线运动的质点的瞬时速度方向在曲线运动的切线方向
B.质点在恒力作用下不可能做曲线运动。
C.质点做曲线运动时受到的合力方向与速度方向一定不在同一直线上
D.质点做曲线运动不一定有加速度
例3.关于运动的性质,下列说法中正确的是【 A 】
A.曲线运动一定是变速运动
B.曲线运动一定是变加速运动
C.变速运动一定是曲线运动
D.变力作用下的物体一定做曲线运动
例4.如图,物体在恒力F 作用下沿曲线从 A 运动到B , 这时突然使它所受力反向(大小不变),则物体以后的运动情况( C )
A、可能沿曲线 Ba运动
B、可能沿直线 Bb 运动
C、可能沿曲线 Bc运动
D、可能沿原曲线由 B 返回 A
第2课时 生活中的运动的合成与分解
思考:乒乓球以某个角度抛出,其运动轨迹不是直线是而是曲线。怎样研究、描述这样的运动呢?
建立平面直角坐标系
一.合运动与分运动:
1、物体实际的运动叫合运动
2、物体同时参与合成运动的运动叫分运动
3、合运动与分运动的关系:
a:等时性---合运动和分运动经历的时间相等。
b:独立性---各分运动独立进行,互不影响。
c:等效性----各分运动的规律叠加起来和合运动的规律等效
小船过河
如图某人乘小船以速度V沿直线从小溪的A处到下游对岸的处.那么我们如何建立坐标系研究小船的运动
根据小船的运动效果,可以这样建立坐标: 以小船的初始位置A为坐标原点,沿河岸和垂直河岸的方向建立直角坐标系.
1、小船位置
小船经过时间t位置P的坐标:x = v1 t,y= v2t
所以经过时间t小船运动的位移 :
位移的方向α(如图):
位移方向不变,所以小船运动轨迹是直线
2、小船速度
求小船经过时间t运动到P点速度
设小船经过时间t运动到P点
在X轴方向上做匀速直线运动,有vX=v1
在Y轴方向上做匀速直线运动,有vY=v2
所以经过时间t小船运动的速度
速度的方向β(如图)
速度大小和方向都不变,所以小船的运动是匀速直线运动
例5.(课本p38例题)跳伞员打开降落伞下落一段时间后的运动可近似视为匀速下落。若无风,跳伞员着地的速度约为5m/s,方向竖直向下;若有风,且风速大小为4m/s,方向水平向东,假设跳伞员在水平方向的速度与风速相等,落地时在竖直方向的速度与水平风速无关,则跳伞员着地的速度将是多大?速度的方向怎样?
答案:6.4m/s ,
探究:两个互成角度的直线运动的合成:
【例题】试分析以下运动的合运动的性质: (从速度、加速度、运动轨迹方面分析)
①互成角度的两个匀速直线运动的合运动:一定是匀速直线运动
②互成角度的一个匀速直线运动和一个匀变速直线运动的合运动:一定是匀变速曲线运动
③互成角度两个初速度为零的匀加速直线运动的合运动:一定是匀加速直线运动
④互成角度的两个初速度不为零的匀变速直线运动的合运动:可能是匀变速直线运动也可能是匀变速曲线运动
小结:
(1)合运动与分运动
在物理学中,如果一个物体实际发生的运动产生的效果跟另外两个运动产生的效果相同,我们就把物体的实际运动叫做这两个运动的合运动,这两个运动叫做这一实际运动的分运动。
(2)合运动与分运动的关系:
等时性——合运动和分运动经历的时间相等。
独立性——各分运动独立进行,互不影响。
等效性——各分运动的规律叠加起来和合运动的规律等效。
(3)运动的合成与分解:
运动的合成与分解遵循平行四边形定则。
三.运动的合成和分解的应用———小船渡河问题
一.小船渡河问题的分析方法:
方法一:小船在有一定流速的水中渡河时,将船渡河的运动看作参与两个方向的分运动,即随水以速度 v水漂流的运动和以速度 v船相对于静水的划行运动,这两个分运动互不干扰具有等时性。
方法二: 将船对水的速度沿平行于河岸和垂直河岸方向正交分解。
注意:船的实际运动 v(相对于河岸的运动)——是合运动。
2.分情况讨论小船渡河问题
第一种情况:v水(1)怎样才能使渡河时间最短
由分运动与合运动的等时性知,让船头垂直对岸运动即可(如下图所示)
船头的指向与船的实际航向不同
最短时间t= , ,
怎样才能使渡河位移最短
小船的运动为实际运动,要使实际运动位移最短只要使合位移最短即可,位移最短为河宽d,船头须向上游倾斜一定角度(如下图所示)
最短的位移为河宽d,船头与上游河岸夹角满足v船cos θ=v水。
第二种情况:v水>v船(设水流速度为v水,船在静水中速度为v船,河宽为d)
(1)怎样才能使渡河时间最短
只要使船头垂直于河岸航行即可,如图所示,此时最短时间t=.
(2)怎样使渡河位移最短
如图所示,从出发点A开始作矢量v水,再以v水末端为圆心,以v船的大小为半径画圆弧,自出发点A向圆弧作切线即为船位移最小时的合运动的方向.这时船头与河岸夹角θ满足cos θ=,最短位移x短=.
例6.已知某船在静水中的速度为v1=5 m/s,现让船渡过某条河,假设这条河的两岸是理想的平行线,河宽为d=100 m,水流速度为v2=3 m/s,方向与河岸平行.
(1)欲使船以最短时间渡河,渡河所用时间是多少?位移有多大?
(2)欲使船以最小位移渡河,渡河所用时间是多少?
(3)若水流速度为v2′=6 m/s,船在静水中的速度为v1=5 m/s不变,船能否垂直河岸渡河.
答案 (1)20 s 20 m (2)25 s (3)不能
解析 (1)由题意知,当船在垂直于河岸方向上的分速度最大时,渡河所用时间最短,河水流速平行于河岸,不影响渡河时间,所以当船头垂直于河岸渡河时,所用时间最短,则最短时间为t== s=20 s.
如图甲所示,当船到达对岸时,船沿水流方向也发生了位移,由几何知识可得,船的位移为l=,由题意可得x=v2t=3×20 m=60 m,代入得l=20 m.
(2)分析可知,当船的实际速度方向垂直于河岸时,船的位移最小,因船在静水中的速度为v1=5 m/s,大于水流速度v2=3 m/s,故可以使船的实际速度方向垂直于河岸.如图乙所示,设船斜指向上游河对岸,且与河岸所成夹角为θ,则有v1cos θ=v2,cos θ==0.6,则sin θ==0.8,所用的时间为t== s=25 s.
(3)当水流速度v2′=6 m/s大于船在静水中的速度v1=5 m/s时,不论v1方向如何,其合速度方向总是偏向下游,故不能垂直河岸渡河.
例7.(多选)若河水的流速大小与水到河岸的距离有关,河中心水的流速最大,河岸边缘处水的流速最小。现假设河的宽度为120 m。河中心水的流速大小为4 m/s,船在静水中的速度大小为3 m/s,要使船以最短时间渡河,则 ( BD )
A.船渡河的最短时间是24 s
B.在行驶过程中,船头始终与河岸垂直
C.船在河水中航行的轨迹是一条直线
D.船在河水中的最大速度为5 m/s
例8.(课本p38迁移)如图所示,一条小船位于宽200m的河的正中间A点处,下游150m处有一危险区,已知小船在静水中的最大速度为3m/s,水流速度为4m/s。为了使小船避开危险区安全到达河岸,船员立刻使船头正对河岸奋力划船,小船能安全到达河岸吗?
答案:能安全到达。
【教材分析】
本节是以后抛体运动、圆周运动的基础,是学好以后知识的基本保证。通过学生举例、图片观察,分析运动特点,猜想曲线运动的方向,之后通过实验验证学生关于曲线运动的速度方向的猜想,并从理论上分析出曲线运动的方向。对于物体做直线运动和曲线运动的条件,首先让学生猜想,然后用实验验证,根据学生实际情况,依据牛顿定律:力、加速度、速度的关系,得出物体做曲线运动的条件。通过小船过河总结出运动的合成与分解的规律。并且运用运动的合成与分解的规律来解决小船渡河等实际问题。
【教学目标与核心素养】
物理观念:能了解曲线运动的内涵,知道物体做曲线运动的条件,掌握运动的合成与分解的规律,并且运用运动的合成与分解的规律来解决小船渡河等实际问题,形成运动的合成与分解的观念。
科学思维:通过探究的过程,让学生体会得到能体会将复杂运动分解为简单运动的物理思想. 科学探究:通过实验探究过程组织学生总结出曲线运动的速度方向;并给予理论证明。
科学态度与责任:能领略曲线运动的奇妙与和谐,发展对科学的好奇心与求知欲。
【教学重难点】
1.重点:理解曲线运动是变速运动,判定物体做曲线运动的方向以及明确物体做曲线运动的条件,并且掌握运动合成与分解的方法。
2.难点:理解合运动和它的分运动是等效替代的关系并且运用运动的合成与分解的规律来解决小船渡河等实际问题。
【教学过程】
【新课导入】
飞镖运动是一项非常有趣的运动。在一次飞镖比赛中,一位同学沿水平方向正对飞镖盘的靶心投出飞镖,飞镖能命中靶心吗?从物理学的角度看,怎样才能投得更准?在田径运动会上,运动员投掷标枪、铅球、铁饼,都会非常注意投掷的角度。如果要参加学校田径运动会的投掷比赛,你知道怎样才能投掷得更远吗?除了力度外,为何还与投掷角度有关?
【新课讲授】
认识曲线运动
一.曲线运动的概念
车辆在弯曲的高架桥上、在弯曲的盘山公路上的运动轨迹是什么图线?绕地球运动的卫星的运动轨迹是什么图线?
定义:运动轨迹是曲线的运动
想一想:如何表达出曲线运动的位移SOA
二.曲线运动的速度
【实验探究】(一)砂轮上打磨下来的炽热微粒飞离砂轮时的情形,微粒在即将离开砂轮时的速度方向如何?
答:火星由于惯性,以脱离砂轮时的速度沿切线方向飞出,切线方向即为火星飞出时的速度方向。
(二)雨滴飞离雨伞时的情形,雨滴在即将离开雨伞时的速度方向如何?
答:水滴沿伞边缘的切线方向飞出。
【实验分析】1、砂轮边缘的沙粒的运动轨迹是什么?火星飞出方向是怎样的
答:砂轮边缘的沙粒的轨迹是个圆,火星从砂轮边缘的切线方向飞出。
水滴运动的轨迹是什么?飞出方向是怎样的
答:水滴随雨伞一起转动,它的轨迹是个圆,水滴从雨伞边缘的切线方向飞出
【实验结论】做曲线运动物体的速度方向是曲线上的某一点切线方向
【理论分析】
瞬时速度
当时间Δt或位移Δx趋近于零时:
曲线运动的质点在某一点(或某一时刻)的速度方向在曲线的这一点的切线方向上。
小结:二、曲线运动的速度:
1、曲线运动的速度方向:
曲线运动中速度的方向是时刻改变的,质点在某一点(或某一时刻)的速度方向在曲线的这一点的切线方向上。
曲线运动的性质:曲线运动是变速运动。
(1)曲线运动一定是变速运动,但变速运动不一定是曲线运动。
(2)只要物体的合外力为恒力,它一定做匀变速运动,可能是直线运动,也可能是曲线运动。
例1:质点沿曲线从左向右运动,画出质点在A、B、C 三点的速度方向。
结论:曲线运动速度方向时刻在改变,是变速运动,加速度a不等于0,合力F不等于0
三.物体做曲线运动的条件
探究实验:钢珠在磁铁吸引下的运动
首先推动钢珠,让钢珠在水平桌面上做直线运动,观察其运动轨迹。然后在其运动轨迹旁放一块磁缺,再次推动钢珠,观察其运动轨迹。解释观察到的现象。
思考:物体做曲线运动的条件是什么?
分析现象:
物体做曲线运动的条件:当物体所受合力的方向和它的速度方向不在同一直线上时,物体做曲线运动。
思考:
做曲线运动的物体运动轨迹、速度方向与其所受合外力方向三者 位置关系如何?
答:物体运动轨迹夹在速度方向和合外力方向之间。
2.做曲线运动的物体运动轨迹弯曲方向与其所受合外力方向有什么关系呢?
答:做曲线运动的物体所受合外力必指向运动轨迹凹的一侧
结论:曲线运动轨迹始终夹在合外力方向与速度方向之间,合外力指向轨迹内侧。
总结:F、a、v三者关系辨析
F合(a) 跟 v 在同一直线上 直线运动
F合(a) 恒定→匀变速直线运动
F合(a) 变化→变加速直线运动
F合(a) 跟 v 不在同一直线上 曲线运动
F合(a) 恒定→匀变速曲线运动
F合(a) 变化→变加速曲线运动
说明:判断直线还是曲线运动关键看a 与v 是否同一直线;判断匀变速还是变加速关键看a 是否恒定
例2.(多选)关于曲线运动,下列说法正确的是【 AC 】
A.做曲线运动的质点的瞬时速度方向在曲线运动的切线方向
B.质点在恒力作用下不可能做曲线运动。
C.质点做曲线运动时受到的合力方向与速度方向一定不在同一直线上
D.质点做曲线运动不一定有加速度
例3.关于运动的性质,下列说法中正确的是【 A 】
A.曲线运动一定是变速运动
B.曲线运动一定是变加速运动
C.变速运动一定是曲线运动
D.变力作用下的物体一定做曲线运动
例4.如图,物体在恒力F 作用下沿曲线从 A 运动到B , 这时突然使它所受力反向(大小不变),则物体以后的运动情况( C )
A、可能沿曲线 Ba运动
B、可能沿直线 Bb 运动
C、可能沿曲线 Bc运动
D、可能沿原曲线由 B 返回 A
第2课时 生活中的运动的合成与分解
思考:乒乓球以某个角度抛出,其运动轨迹不是直线是而是曲线。怎样研究、描述这样的运动呢?
建立平面直角坐标系
一.合运动与分运动:
1、物体实际的运动叫合运动
2、物体同时参与合成运动的运动叫分运动
3、合运动与分运动的关系:
a:等时性---合运动和分运动经历的时间相等。
b:独立性---各分运动独立进行,互不影响。
c:等效性----各分运动的规律叠加起来和合运动的规律等效
小船过河
如图某人乘小船以速度V沿直线从小溪的A处到下游对岸的处.那么我们如何建立坐标系研究小船的运动
根据小船的运动效果,可以这样建立坐标: 以小船的初始位置A为坐标原点,沿河岸和垂直河岸的方向建立直角坐标系.
1、小船位置
小船经过时间t位置P的坐标:x = v1 t,y= v2t
所以经过时间t小船运动的位移 :
位移的方向α(如图):
位移方向不变,所以小船运动轨迹是直线
2、小船速度
求小船经过时间t运动到P点速度
设小船经过时间t运动到P点
在X轴方向上做匀速直线运动,有vX=v1
在Y轴方向上做匀速直线运动,有vY=v2
所以经过时间t小船运动的速度
速度的方向β(如图)
速度大小和方向都不变,所以小船的运动是匀速直线运动
例5.(课本p38例题)跳伞员打开降落伞下落一段时间后的运动可近似视为匀速下落。若无风,跳伞员着地的速度约为5m/s,方向竖直向下;若有风,且风速大小为4m/s,方向水平向东,假设跳伞员在水平方向的速度与风速相等,落地时在竖直方向的速度与水平风速无关,则跳伞员着地的速度将是多大?速度的方向怎样?
答案:6.4m/s ,
探究:两个互成角度的直线运动的合成:
【例题】试分析以下运动的合运动的性质: (从速度、加速度、运动轨迹方面分析)
①互成角度的两个匀速直线运动的合运动:一定是匀速直线运动
②互成角度的一个匀速直线运动和一个匀变速直线运动的合运动:一定是匀变速曲线运动
③互成角度两个初速度为零的匀加速直线运动的合运动:一定是匀加速直线运动
④互成角度的两个初速度不为零的匀变速直线运动的合运动:可能是匀变速直线运动也可能是匀变速曲线运动
小结:
(1)合运动与分运动
在物理学中,如果一个物体实际发生的运动产生的效果跟另外两个运动产生的效果相同,我们就把物体的实际运动叫做这两个运动的合运动,这两个运动叫做这一实际运动的分运动。
(2)合运动与分运动的关系:
等时性——合运动和分运动经历的时间相等。
独立性——各分运动独立进行,互不影响。
等效性——各分运动的规律叠加起来和合运动的规律等效。
(3)运动的合成与分解:
运动的合成与分解遵循平行四边形定则。
三.运动的合成和分解的应用———小船渡河问题
一.小船渡河问题的分析方法:
方法一:小船在有一定流速的水中渡河时,将船渡河的运动看作参与两个方向的分运动,即随水以速度 v水漂流的运动和以速度 v船相对于静水的划行运动,这两个分运动互不干扰具有等时性。
方法二: 将船对水的速度沿平行于河岸和垂直河岸方向正交分解。
注意:船的实际运动 v(相对于河岸的运动)——是合运动。
2.分情况讨论小船渡河问题
第一种情况:v水
由分运动与合运动的等时性知,让船头垂直对岸运动即可(如下图所示)
船头的指向与船的实际航向不同
最短时间t= , ,
怎样才能使渡河位移最短
小船的运动为实际运动,要使实际运动位移最短只要使合位移最短即可,位移最短为河宽d,船头须向上游倾斜一定角度(如下图所示)
最短的位移为河宽d,船头与上游河岸夹角满足v船cos θ=v水。
第二种情况:v水>v船(设水流速度为v水,船在静水中速度为v船,河宽为d)
(1)怎样才能使渡河时间最短
只要使船头垂直于河岸航行即可,如图所示,此时最短时间t=.
(2)怎样使渡河位移最短
如图所示,从出发点A开始作矢量v水,再以v水末端为圆心,以v船的大小为半径画圆弧,自出发点A向圆弧作切线即为船位移最小时的合运动的方向.这时船头与河岸夹角θ满足cos θ=,最短位移x短=.
例6.已知某船在静水中的速度为v1=5 m/s,现让船渡过某条河,假设这条河的两岸是理想的平行线,河宽为d=100 m,水流速度为v2=3 m/s,方向与河岸平行.
(1)欲使船以最短时间渡河,渡河所用时间是多少?位移有多大?
(2)欲使船以最小位移渡河,渡河所用时间是多少?
(3)若水流速度为v2′=6 m/s,船在静水中的速度为v1=5 m/s不变,船能否垂直河岸渡河.
答案 (1)20 s 20 m (2)25 s (3)不能
解析 (1)由题意知,当船在垂直于河岸方向上的分速度最大时,渡河所用时间最短,河水流速平行于河岸,不影响渡河时间,所以当船头垂直于河岸渡河时,所用时间最短,则最短时间为t== s=20 s.
如图甲所示,当船到达对岸时,船沿水流方向也发生了位移,由几何知识可得,船的位移为l=,由题意可得x=v2t=3×20 m=60 m,代入得l=20 m.
(2)分析可知,当船的实际速度方向垂直于河岸时,船的位移最小,因船在静水中的速度为v1=5 m/s,大于水流速度v2=3 m/s,故可以使船的实际速度方向垂直于河岸.如图乙所示,设船斜指向上游河对岸,且与河岸所成夹角为θ,则有v1cos θ=v2,cos θ==0.6,则sin θ==0.8,所用的时间为t== s=25 s.
(3)当水流速度v2′=6 m/s大于船在静水中的速度v1=5 m/s时,不论v1方向如何,其合速度方向总是偏向下游,故不能垂直河岸渡河.
例7.(多选)若河水的流速大小与水到河岸的距离有关,河中心水的流速最大,河岸边缘处水的流速最小。现假设河的宽度为120 m。河中心水的流速大小为4 m/s,船在静水中的速度大小为3 m/s,要使船以最短时间渡河,则 ( BD )
A.船渡河的最短时间是24 s
B.在行驶过程中,船头始终与河岸垂直
C.船在河水中航行的轨迹是一条直线
D.船在河水中的最大速度为5 m/s
例8.(课本p38迁移)如图所示,一条小船位于宽200m的河的正中间A点处,下游150m处有一危险区,已知小船在静水中的最大速度为3m/s,水流速度为4m/s。为了使小船避开危险区安全到达河岸,船员立刻使船头正对河岸奋力划船,小船能安全到达河岸吗?
答案:能安全到达。
同课章节目录
- 第1章 功和机械能
- 导入 神奇之能
- 第1节 机械功
- 第2节 功率
- 第3节 动能和动能定理
- 第4节 势能及其改变
- 第5节 科学验证:机械能守恒定律
- 第2章 抛体运动
- 导入 更准、更远
- 第1节 运动的合成与分解
- 第2节 平抛运动
- 第3节 科学探究:平抛运动的特点
- 第4节 生活中的抛体运动
- 第3章 圆周运动
- 导入 生活中的圆周运动
- 第1节 匀速圆周运动快慢的描述
- 第2节 科学探究:向心力
- 第3节 离心现象
- 第4章 万有引力定律及航天
- 导入 从嫦娥奔月到“阿波罗”上天
- 第2节 万有引力定律的应用
- 第3节 人类对太空的不懈探索
- 第5章 科学进步无止境
- 导入 再次跨越时空的对话
- 第1节 初识相对论
- 第2节 相对论中的神奇时空
- 第3节 探索宇宙的奥秘
