山东省邹城市第八中学2016届九年级下学期第一次月考数学试题(答案不全)
文档属性
| 名称 | 山东省邹城市第八中学2016届九年级下学期第一次月考数学试题(答案不全) |
|
|
| 格式 | zip | ||
| 文件大小 | 276.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-04-15 00:00:00 | ||
图片预览



文档简介
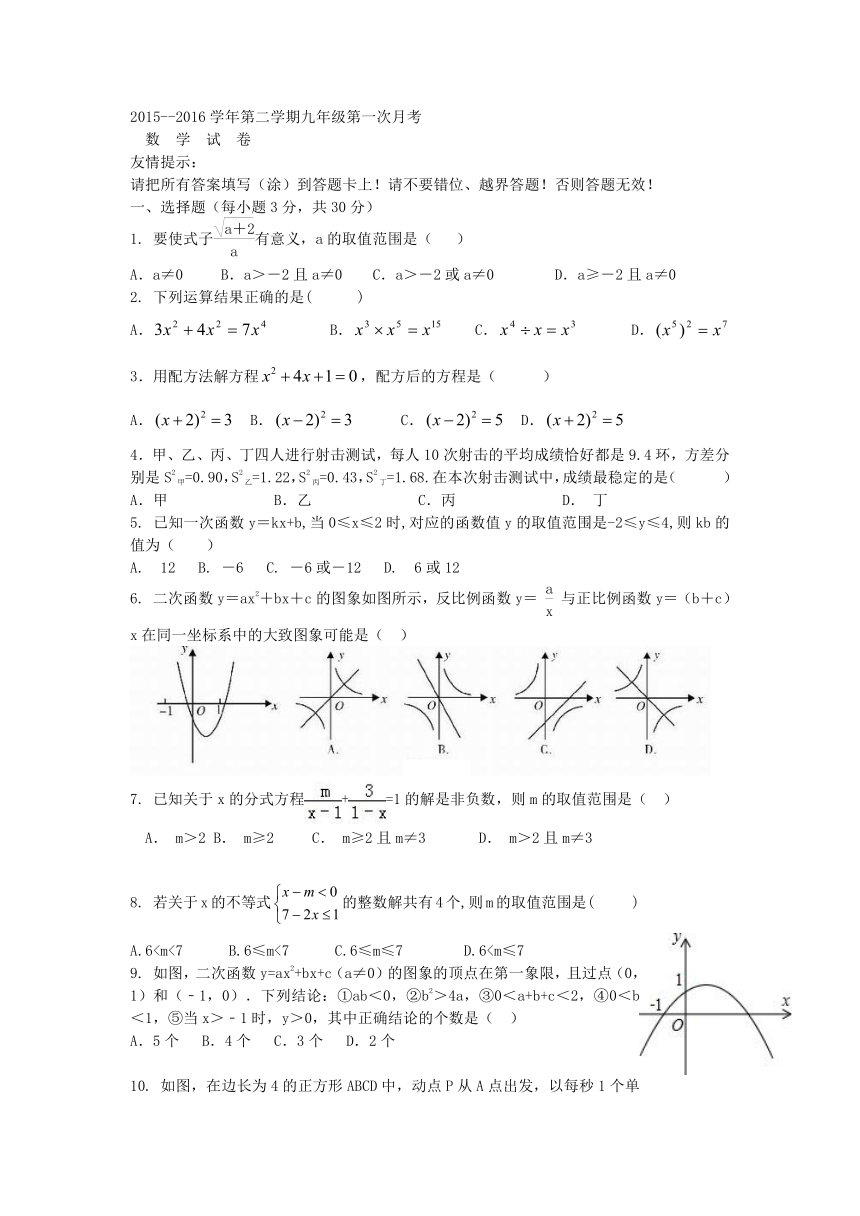
2015--2016学年第二学期九年级第一次月考
数 学 试 卷
友情提示:
请把所有答案填写(涂)到答题卡上!请不要错位、越界答题!否则答题无效!
一、选择题(每小题3分,共30分)
1. 要使式子有意义,a的取值范围是( )
A.a≠0 B.a>-2且a≠0 C.a>-2或a≠0 D.a≥-2且a≠0
2. 下列运算结果正确的是( )
A. B. C. D.
3.用配方法解方程,配方后的方程是( )
A. B. C. D.
4.甲、乙、丙、丁四人进行射击测试,每人 ( http: / / www.21cnjy.com )10次射击的平均成绩恰好都是9.4环,方差分别是S2甲=0.90,S2乙=1.22,S2丙=0.43,S2丁=1.68.在本次射击测试中,成绩最稳定的是( )
A.甲 B.乙 C.丙 D. 丁
5. 已知一次函数y=kx+b,当0≤x≤2时,对应的函数值y的取值范围是-2≤y≤4,则kb的值为( )
A. 12 B. -6 C. -6或-12 D. 6或12
6. 二次函数y=ax2+bx+c的图象如图所示,反比例函数y= 与正比例函数y=(b+c)x在同一坐标系中的大致图象可能是( )
7. 已知关于x的分式方程+=1的解是非负数,则m的取值范围是( )
A. m>2 B. m≥2 C. m≥2且m≠3 D. m>2且m≠3
8. 若关于x的不等式的整数解共有4个,则m的取值范围是( )
A.69. 如图,二次函数y=ax2+bx+c( ( http: / / www.21cnjy.com )a≠0)的图象的顶点在第一象限,且过点(0,1)和(﹣1,0).下列结论:①ab<0,②b2>4a,③0<a+b+c<2,④0<b<1,⑤当x>﹣1时,y>0,其中正确结论的个数是( )
A.5个 B.4个 C.3个 D.2个
10. 如图,在边长为4的正方形ABCD中,动点P从A点出发,以每秒1个单位长度的速度沿AB向B点运动,同时动点Q从B点出发,以每秒2个单位长度的速度沿BC→CD方向运动,当P运动到B点时,P,Q两点同时停止运动.设P点运动的时间为t,△APQ的面积为S,则S与t的函数关系的图象是( )
( http: / / www.21cnjy.com )
二、填空题(每小题3分,共15分)
11. 如果方程ax2+2x+1=0有两个不等实数根,则实数a的取值范围是
12. 分解因式:=________________.
13. 将抛物线向上平移2个单位,再向右平移1个单位后,得到的抛物线的解析式为____________.
14. 已知:与 || 互为相反数,则式子的值等于 。
15. 正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…按如图的方式
放置.点A1,A2,A3,…和点C1,C2,C3,…分别在直线
y=x+1和x轴上,则点B6的坐标是__________
三、解答题
16.(1) (本小题4分)计算:.
(2) (本小题5分)先化简:,然后请你从的范围内取一个合适的整数的值代入求值.
17. (本小题8分)在复习《反比例函数》一课时,同桌的小峰和小轩有一个问题观点不一致:
情境:随机同时掷两枚质地均匀的骰子(骰子六 ( http: / / www.21cnjy.com )个面上的点数分别代表1,2,3,4,5,6),第一枚骰子上的点数作为点P(m,n)的横坐标,第二枚骰子上的点数作为点P(m,n)的纵坐标.
小峰认为:点P(m,n)在反比例函数图象上的概率一定大于反比例函数图象上的概率;
小轩认为:点P(m,n)在反比例函数和图象上的概率相同.
问题:(1)试用列表或画树状图的方法,列举出所有点P(m,n)的情形;
(2)分别求出点P(m,n)在两个反比例函数图象上的概率,并说明谁的观点正确.
18.(本小题6分)如图, ( http: / / www.21cnjy.com )在直角坐标系中,矩形OABC的顶点O与坐标原点重合,顶点A,C分别在坐标轴上,顶点B的坐标为(4,2).过点D(0,3)和E(6,0)的直线分别与AB,BC交于点M,N.
(1)求直线DE的解析式和点M的坐标;
(2)若反比例函数(x>0)的图象经过点M,求该反比例函数的解析式,并通过计算判断点N是否在该函数的图象上;
(3)若反比例函数(x>0)的图象与△MNB有公共点,请直接写出m的取值范围.
19. (本题满分8分).某新建的商场有3000m2的地面花岗岩需要铺设,现有甲、乙两个工程队希望承包铺设地面的过程:甲工程队平均每天比乙工程队多铺50m2,甲工程队单独完成该工程的工期是乙工程队单独完成该工程所需工期的;
(1)求甲、乙两个工程队完成该工程各需几天?
(2)由于该工程的施工时间不能超过14天,商场考虑先让乙工程队做m天,剩下的工程由甲、乙两队共同完成,求m的最大值.
20.(本小题9分)某商品的进价为每件40元,售价为每件50元,每个月可卖出210件;如果每件商品的售价每上涨1元,则每个月少卖10件(每件售价不能高于65元).设每件商品的售价上涨元(为正整数),每个月的销售利润为元.
(1)求与的函数关系式并直接写出自变量的取值范围;
(2)每件商品的售价定为多少元时,每个月可获得最大利润?最大的月利润是多少元?
(3)每件商品的售价定为多少元时,每个月的利润恰为2200元?根据以上结论,请你直接写出售价在什么范围时,每个月的利润不低于2200元?
21.(本小题6分)设a,b是任意两个不等实数,我们规定:满足不等式a≤x≤b的实数x的所有取值的全体叫做闭区间,表示为[a,b].对于一个函数,如果它的自变量x与函数值y满足:当m≤x≤n时,有m≤y≤n,我们就称此函数是闭区间[m.n]上的“闭函数”.如函数,当x=1时,y=3;当x=3时,y=1,即当时,有,所以说函数是闭区间[1,3]上的“闭函数”.
(1)反比例函数y=是闭区间[1,2015]上的“闭函数”吗?请判断并说明理由;
(2)若二次函数y=是闭区间[1,2]上的“闭函数”,求k的值;
(3)若一次函数y=kx+b(k≠0)是闭区间[m,n]上的“闭函数”,求此函数的解析式(用含m,n的代数式表示).
22.(本小题9分)如图,已知抛物线与轴交于A、B两点,与轴交于点C.
(1)求A、B、C三点的坐标.
(2)过点A作AP∥CB交抛物线于点P,求四边形ACBP的面积.
(3)在轴上方的抛物线上是否存在一点M,过M作MG轴于点G,使以A、M、G三点为顶点的三角形与PCA相似.若存在,请求出M点的坐标;否则,请说明理由.
答案
22.解:(1)令,得 解得
令,得
∴ A B C 3分
(2)∵OA=OB=OC= ∴BAC=ACO=BCO=
∵AP∥CB, ∴PAB=
过点P作PE轴于E,则APE为等腰直角三角形
令OE=,则PE= ∴P
∵点P在抛物线上 ∴
解得,(不合题意,舍去)
∴PE= 4分
∴四边形ACBP的面积=AB OC+AB PE
= 5分
(3). 假设存在
∵PAB=BAC = ∴PAAC
∵MG轴于点G, ∴MGA=PAC =
在Rt△AOC中,OA=OC= ∴AC=
在Rt△PAE中,AE=PE= ∴AP= 6分
设M点的横坐标为,则M
①点M在轴左侧时,则
(ⅰ) 当AMG PCA时,有=
∵AG=,MG=
即
解得(舍去) (舍去)………7分
(ⅱ) 当MAG PCA时有=
即
解得:(舍去)
∴M 8分
② 点M在轴右侧时,则
(ⅰ) 当AMG PCA时有=
∵AG=,MG=
∴
解得(舍去)
∴M ………………………9分
(ⅱ) 当MAGPCA时有=
即
解得:(舍去)
∴M ………………………………10分
∴存在点M,使以A、M、G三点为顶点的三角形与PCA相似
M点的坐标为,, 11分
说明:以上各题如有其他解(证)法,请酌情给分
x
M
N
y
D
A
B
C
E
O
C
P
B
y
A
E
C
B
y
P
A
G
M
C
B
y
P
A
G
M
C
B
y
P
A
数 学 试 卷
友情提示:
请把所有答案填写(涂)到答题卡上!请不要错位、越界答题!否则答题无效!
一、选择题(每小题3分,共30分)
1. 要使式子有意义,a的取值范围是( )
A.a≠0 B.a>-2且a≠0 C.a>-2或a≠0 D.a≥-2且a≠0
2. 下列运算结果正确的是( )
A. B. C. D.
3.用配方法解方程,配方后的方程是( )
A. B. C. D.
4.甲、乙、丙、丁四人进行射击测试,每人 ( http: / / www.21cnjy.com )10次射击的平均成绩恰好都是9.4环,方差分别是S2甲=0.90,S2乙=1.22,S2丙=0.43,S2丁=1.68.在本次射击测试中,成绩最稳定的是( )
A.甲 B.乙 C.丙 D. 丁
5. 已知一次函数y=kx+b,当0≤x≤2时,对应的函数值y的取值范围是-2≤y≤4,则kb的值为( )
A. 12 B. -6 C. -6或-12 D. 6或12
6. 二次函数y=ax2+bx+c的图象如图所示,反比例函数y= 与正比例函数y=(b+c)x在同一坐标系中的大致图象可能是( )
7. 已知关于x的分式方程+=1的解是非负数,则m的取值范围是( )
A. m>2 B. m≥2 C. m≥2且m≠3 D. m>2且m≠3
8. 若关于x的不等式的整数解共有4个,则m的取值范围是( )
A.6
A.5个 B.4个 C.3个 D.2个
10. 如图,在边长为4的正方形ABCD中,动点P从A点出发,以每秒1个单位长度的速度沿AB向B点运动,同时动点Q从B点出发,以每秒2个单位长度的速度沿BC→CD方向运动,当P运动到B点时,P,Q两点同时停止运动.设P点运动的时间为t,△APQ的面积为S,则S与t的函数关系的图象是( )
( http: / / www.21cnjy.com )
二、填空题(每小题3分,共15分)
11. 如果方程ax2+2x+1=0有两个不等实数根,则实数a的取值范围是
12. 分解因式:=________________.
13. 将抛物线向上平移2个单位,再向右平移1个单位后,得到的抛物线的解析式为____________.
14. 已知:与 || 互为相反数,则式子的值等于 。
15. 正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…按如图的方式
放置.点A1,A2,A3,…和点C1,C2,C3,…分别在直线
y=x+1和x轴上,则点B6的坐标是__________
三、解答题
16.(1) (本小题4分)计算:.
(2) (本小题5分)先化简:,然后请你从的范围内取一个合适的整数的值代入求值.
17. (本小题8分)在复习《反比例函数》一课时,同桌的小峰和小轩有一个问题观点不一致:
情境:随机同时掷两枚质地均匀的骰子(骰子六 ( http: / / www.21cnjy.com )个面上的点数分别代表1,2,3,4,5,6),第一枚骰子上的点数作为点P(m,n)的横坐标,第二枚骰子上的点数作为点P(m,n)的纵坐标.
小峰认为:点P(m,n)在反比例函数图象上的概率一定大于反比例函数图象上的概率;
小轩认为:点P(m,n)在反比例函数和图象上的概率相同.
问题:(1)试用列表或画树状图的方法,列举出所有点P(m,n)的情形;
(2)分别求出点P(m,n)在两个反比例函数图象上的概率,并说明谁的观点正确.
18.(本小题6分)如图, ( http: / / www.21cnjy.com )在直角坐标系中,矩形OABC的顶点O与坐标原点重合,顶点A,C分别在坐标轴上,顶点B的坐标为(4,2).过点D(0,3)和E(6,0)的直线分别与AB,BC交于点M,N.
(1)求直线DE的解析式和点M的坐标;
(2)若反比例函数(x>0)的图象经过点M,求该反比例函数的解析式,并通过计算判断点N是否在该函数的图象上;
(3)若反比例函数(x>0)的图象与△MNB有公共点,请直接写出m的取值范围.
19. (本题满分8分).某新建的商场有3000m2的地面花岗岩需要铺设,现有甲、乙两个工程队希望承包铺设地面的过程:甲工程队平均每天比乙工程队多铺50m2,甲工程队单独完成该工程的工期是乙工程队单独完成该工程所需工期的;
(1)求甲、乙两个工程队完成该工程各需几天?
(2)由于该工程的施工时间不能超过14天,商场考虑先让乙工程队做m天,剩下的工程由甲、乙两队共同完成,求m的最大值.
20.(本小题9分)某商品的进价为每件40元,售价为每件50元,每个月可卖出210件;如果每件商品的售价每上涨1元,则每个月少卖10件(每件售价不能高于65元).设每件商品的售价上涨元(为正整数),每个月的销售利润为元.
(1)求与的函数关系式并直接写出自变量的取值范围;
(2)每件商品的售价定为多少元时,每个月可获得最大利润?最大的月利润是多少元?
(3)每件商品的售价定为多少元时,每个月的利润恰为2200元?根据以上结论,请你直接写出售价在什么范围时,每个月的利润不低于2200元?
21.(本小题6分)设a,b是任意两个不等实数,我们规定:满足不等式a≤x≤b的实数x的所有取值的全体叫做闭区间,表示为[a,b].对于一个函数,如果它的自变量x与函数值y满足:当m≤x≤n时,有m≤y≤n,我们就称此函数是闭区间[m.n]上的“闭函数”.如函数,当x=1时,y=3;当x=3时,y=1,即当时,有,所以说函数是闭区间[1,3]上的“闭函数”.
(1)反比例函数y=是闭区间[1,2015]上的“闭函数”吗?请判断并说明理由;
(2)若二次函数y=是闭区间[1,2]上的“闭函数”,求k的值;
(3)若一次函数y=kx+b(k≠0)是闭区间[m,n]上的“闭函数”,求此函数的解析式(用含m,n的代数式表示).
22.(本小题9分)如图,已知抛物线与轴交于A、B两点,与轴交于点C.
(1)求A、B、C三点的坐标.
(2)过点A作AP∥CB交抛物线于点P,求四边形ACBP的面积.
(3)在轴上方的抛物线上是否存在一点M,过M作MG轴于点G,使以A、M、G三点为顶点的三角形与PCA相似.若存在,请求出M点的坐标;否则,请说明理由.
答案
22.解:(1)令,得 解得
令,得
∴ A B C 3分
(2)∵OA=OB=OC= ∴BAC=ACO=BCO=
∵AP∥CB, ∴PAB=
过点P作PE轴于E,则APE为等腰直角三角形
令OE=,则PE= ∴P
∵点P在抛物线上 ∴
解得,(不合题意,舍去)
∴PE= 4分
∴四边形ACBP的面积=AB OC+AB PE
= 5分
(3). 假设存在
∵PAB=BAC = ∴PAAC
∵MG轴于点G, ∴MGA=PAC =
在Rt△AOC中,OA=OC= ∴AC=
在Rt△PAE中,AE=PE= ∴AP= 6分
设M点的横坐标为,则M
①点M在轴左侧时,则
(ⅰ) 当AMG PCA时,有=
∵AG=,MG=
即
解得(舍去) (舍去)………7分
(ⅱ) 当MAG PCA时有=
即
解得:(舍去)
∴M 8分
② 点M在轴右侧时,则
(ⅰ) 当AMG PCA时有=
∵AG=,MG=
∴
解得(舍去)
∴M ………………………9分
(ⅱ) 当MAGPCA时有=
即
解得:(舍去)
∴M ………………………………10分
∴存在点M,使以A、M、G三点为顶点的三角形与PCA相似
M点的坐标为,, 11分
说明:以上各题如有其他解(证)法,请酌情给分
x
M
N
y
D
A
B
C
E
O
C
P
B
y
A
E
C
B
y
P
A
G
M
C
B
y
P
A
G
M
C
B
y
P
A
同课章节目录
