2024-2025学年北师大版五年级数学上册期末模拟卷(含答案)
文档属性
| 名称 | 2024-2025学年北师大版五年级数学上册期末模拟卷(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 627.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-08 00:00:00 | ||
图片预览




文档简介
保密★启用前
20224-2025学年五年级上册期末模拟卷(北师大版)
数学
考试范围:五上全册 考试时间:100分钟 分值:100分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
一、精挑细选,慎重选择。(请在答题卡相应位置作答)(共9分)
1.淘气一个月看完一本书,这个月上旬,他看完了总页数的,中旬看了剩下的,中旬看了总页数的( )
A. B. C. D.
2.要得到左面的图案,应将正方形纸按( )的方式剪掉涂色部分。
A. B. C.
3.下列说法中,正确的有( )个。
①0是最小的自然数
②一个数最少有两个因数
③是质数的一定是奇数,是偶数的一定是合数
④任意三个连续自然数的和一定是3的倍数
A.1 B.2 C.3 D.4
4.哥德巴赫猜想:“任意一个大于2的偶数都可以表示成两个质数的和”。下面的算式中符合这个猜想的是( )。
A.10=2+8 B.16=3+13 C.14=5+9 D.8=7+1
5.如图,把大长方形的面积看成单位“1”,则斜线部分的面积用算式( )表示。
A. B. C.
6.下边的算式没有算完,根据算式,商是( )。
A.0.68 B. C. D.无法确定
7.某市高新区规划了一个正方形的居民活动中心,周长是1600米,它的面积是( )。
A.1600公顷 B.16000平方米 C.16公顷
8.妙妙和聪聪玩拼数游戏,在如图四张卡片中,任意选三张组成三位数,在这些数中同时是2、3和5的倍数的有( )个。
A.2 B.4 C.6 D.8
9.桌子上摆着10张卡片,上面写着1至10十个数字,任意抽取一张卡片,笑笑设计以下游戏规则,哪一种规则不公平 ( )
A.抽到奇数笑笑赢,抽到偶数妙想赢。
B.抽到数字大于5的卡片笑笑赢,抽到数字小于5的卡片妙想赢。
C.抽到有1、3、4、7、8这五个数字中任意一个数字的卡片则笑笑赢,抽到其它卡片则妙想赢。
D.如果抽到的卡片上数字是1或者质数,笑笑赢;如果抽到的卡片上数字是合数,妙想赢。
二、火眼金睛,细心裁判。(共6分)
10.在除法中,如果除不尽则商一定是无限循环小数。 ( )
11.两个质数相乘的积一定是偶数。( )
12.周长相等的长方形和正方形,面积相比,正方形的面积大些。( )
13.一个长方形的木条框,拉住它的两个对角,使它变成一个平行四边形,拉出的平行四边形和原来的长方形周长没变,面积变了。( )
14.时光一去不复返。
15.两个等底等高的平行四边形,形状一定相同。
三、欢乐填空,对号入座。(把答案填到答题卡相应位置上)(共23分)。
16.古诗“春水春池满,春时春草生。春人饮春酒,春鸟弄春声。”在这首诗中出现次数最多的一个字占全诗总字数的 ,这个分数的分数单位是 ,再添上 个这样的分数单位就是最小的质数。
17.周末奇奇用爸爸的围棋棋子摆放了一系列的图形,这些图形蕴含一定的规律。
请观察以上各图,在方框中按规律补齐。
18.下图中,直线上的A点用分数表示是 ,再添上 个它的分数单位后就变成最小的质数。
19.350 m 的 是 的 是 比 多 。
20.“一箱苹果吃去了。”这是把 看做单位“1”,把它平均分成了 份,吃去的苹果有这样的 份,由此可以推出剩下这箱苹果的 。
21.在横线上填上“>”、“<”或“=”。
5.18×0.99 5.18÷0.99 0.89÷0.5 0.89×2
0.66
22.3÷5= = ÷35= = (填小数)
23.某小学开展以“学劳动、会劳动、爱劳动”为主题的多彩劳动课堂。五年级分到一块平行四边形劳动基地,如图,其中梯形区域种植蔬菜,三角形区域种植农作物。已知农作物的种植面积是89.25m2,那么蔬菜的种植面积是 m2。
24.自行车和三轮车一共有10辆,数一数它们的轮子有27个。三轮车有 辆,自行车有 辆。
25. 一种玻璃瓶可以装 0.8 千克花生油。现有 4.5 千克花生油, 用这种玻璃瓶来装完,至少需要这种玻璃瓶 个。
四、耐心审题,巧思妙算。(共32分)
26.直接写出得数。
8.1×100= 0.25×6= 0.05×0.04 = 0.3×50=
0.72÷8= 2.8÷100= 0.3÷0.03= 1.4÷0.04=
竖式计算。
6.3÷0.42= 1.25×0.72= 23.8÷0.17=
28.脱式计算、能简算的要简算。
29.计算下面各图形的面积。
(1)
(2)
五、仔细观察,认真操作。(共6分)
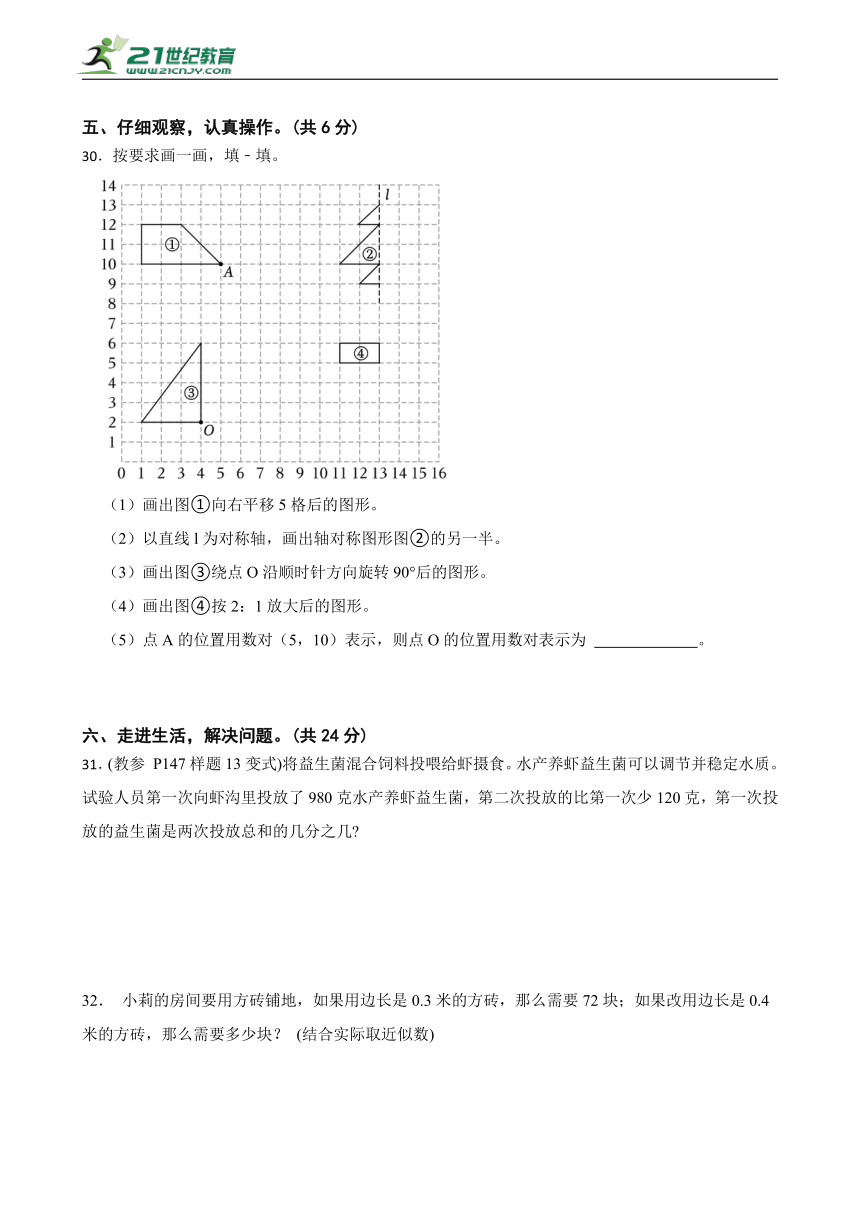
30.按要求画一画,填﹣填。
(1)画出图①向右平移5格后的图形。
(2)以直线l为对称轴,画出轴对称图形图②的另一半。
(3)画出图③绕点O沿顺时针方向旋转90°后的图形。
(4)画出图④按2:1放大后的图形。
(5)点A的位置用数对(5,10)表示,则点O的位置用数对表示为 。
六、走进生活,解决问题。(共24分)
31.(教参 P147样题13变式)将益生菌混合饲料投喂给虾摄食。水产养虾益生菌可以调节并稳定水质。试验人员第一次向虾沟里投放了980克水产养虾益生菌,第二次投放的比第一次少120克,第一次投放的益生菌是两次投放总和的几分之几
小莉的房间要用方砖铺地,如果用边长是0.3米的方砖,那么需要72块;如果改用边长是0.4米的方砖,那么需要多少块? (结合实际取近似数)
某商店分别花同样多的钱,购进甲、乙、丙三种不同的糖果。已知甲、乙、丙三种糖果每千克的价格分别是10元、12元、15元。如果把这三种糖果混合成什锦糖,按20%的利润定价,那么这种什锦糖每千克定价多少元
34.如下图,DE把平行四边形 ABCD分成了一个三角形和一个梯形,且EB=2AE。已知三角形ADE 的面积是10cm2, 则 梯 形BCDE 的面积是( ) cm2 。请写出主要过程。
35. 小货车司机王叔叔需要运送一批家具,通过国道或者高速进行运输的距离相同,根据往常的经验,走国道油耗66升,走高速油耗57升。高速需收取过路费270元。
(1)选择哪条路线更划算 (油价8元/升)
(2)已知本次运输中,该车走国道每百公里油耗比高速多3升,国道限速60公里/小时,高速的限速是100公里/小时,王叔叔在不超速和不违反疲劳驾驶规定的情况下按最大速度行驶,选择两种方式将货物送达的时间差是多少分钟
根据相关观定:驾驶员连续驾驶4小时机动车,至少需停车休息20分钟,否则将构成疲劳驾驶
答案解析部分
1.A
解:(1-)×
=×
=。
故答案为:A。
淘气中旬看了总页数分率=(1-上旬看的分率) ×。
2.A
解:应将正方形纸按 的方式剪掉涂色部分。
故答案为:A。
按 的方式剪掉涂色部分后就得到一个正六边形。
3.B
解:①自然数是大于或等于0的整数,所以0是最小的自然数,此说法正确;
②1只含有1一个因数,此说法错误;
③2是质数但是偶数,此说法错误;
④设三个连续自然数中的第一个为a,则三个连续自然数的和为a+(a+1)+(a+2)=3a+3=3×(a+1),所以任意三个连续自然数的和一定是3的倍数,此说法正确。
故答案为:B。
我们在数物体的时候,用来表示物体个数的0,1,2,3……叫做自然数;
1只有1个因数,就是它自己;
能被2整除的数叫做偶数;不能被2整除的数叫做奇数;
一个数,如果只有1和它本身两个因数,这样的数叫做质数;
任意两个相邻自然数的差是1,任意三个连续自然数的和一定是3的倍数。
4.B
解:选项A, 10=2+8,10是偶数,2是质数,但是8是合数,与题意不符;
选项B, 16=3+13,16是偶数,3和13都是质数,与题意相符;
选项C, 14=5+9,14是偶数,5是质数,9是合数,与题意不符;
选项D, 8=7+1,8是偶数,7是质数,1既不是质数也不是合数,与题意不符。
故答案为:B。
能被2整除的数叫做偶数;不能被2整除的数叫做奇数;
一个数,如果只有1和它本身两个因数,这样的数叫做质数;分别判断各选项的数据即可。
5.B
解:4份涂色,表示,1份涂斜线,表示,所以算式是 。
股答案为:B
把大长方形的面积看成单位“1”,把它平均分成5份,每份是它的,其中4份涂色,表示;再把涂色部分看作单位“1”,把它平均分成3份,每份是它的,其中1份涂斜线,表示,求斜线部分的面积就是求的是多少,用乘法 计算。
6.B
解:观察下面竖式发现余数8已经开始重复出现,也就是商后面的数会重复出现,“0.68”中的末尾是8,8会重复出现,所以商是。
故答案为:B。
循环小数是从小数部分的某一位起,一个数字或几个数字,依次不断地重复出现的小数。一个循环小数的小数部分,依次不断重复出现的数字,就是这个循环小数的循环节。写循环小数时,可以只写第一个循环节,并在这个循环节的首位和末尾数字上面各记一个圆点。
7.C
解:1600÷4=400(米)
400×400=160000(平方米)
160000平方米÷10000=16公顷
它的面积是16公顷
故答案为:C。
正方形的周长÷4=正方形的边长,正方形的边长×正方形的边长=正方形的面积,平方米÷10000=公顷。
8.B
解:既是2的倍数又是5的倍数的三位数末位是0,各个数位上的数字之和是3的倍数的数,就是3的倍数,所以百位上的数字和十位上的数字之和要是3的倍数,4+5=9=3×3, 5+7=12=3×4, 4+7=11, 11不是3的倍数,所以任意选三张组成三位数,在这些数中同时是2、3 和5的倍数的是 450、540、570、750, 共4个。
故答案为:B。
同时是2、3、5的倍数的数的特征:一个数各个数位上的数字之和是3的倍数,个位是0,据此解答。
9.B
解:选项A,1至10十个数字,有5个奇数,5个偶数,任意抽取一张卡片,抽到奇数和偶数的可能性相等,游戏规则是公平的;
选项B,大于5的卡片有6、7、8、9、10,小于5的卡片有1、2、3、4,任意抽取一张卡片,抽到大于5的可能性大,游戏规则不公平;
选项C,一共有10个数字,抽到有1、3、4、7、8这五个数字中任意一个数字的卡片则笑笑赢,抽到其它卡片则妙想赢,此游戏规则公平;
选项D,从1到10十个数字中,1和质数有2、3、5、7共5个数,剩下5个是合数,如果抽到的卡片上数字是1或者质数,笑笑赢;如果抽到的卡片上数字是合数,妙想赢,此游戏规则公平。
故答案为:B。
此题主要考查了游戏规则的公平性,1至10十个数字,奇数有:1、3、5、7、9,偶数有:2、4、6、8、10;质数有2、3、5、7,合数有4、6、8、9、10;大于5的数字有6、7、8、9、10,小于5的数字有1、2、3、4,分别对比抽到情况的可能性,可能性相等,游戏规则公平,否则,不公平。
10.错误
解:在除法中,如果除不尽,商可能是循环小数,也可能是无限不循环小数,原题说法错误。
故答案为:错误。
小数分为有限小数和无限小数,无限小数分为无限不循环小数和循环小数,据此判断。
11.错误
解:假设这两个质数分别为3和5,那么3×5=15,15是奇数;
故答案为:错误。
质数×质数=合数,但不一定是偶数。
12.正确
解:假设长方形和正方形的周长是16。
(5+3)×2
=8×2
=16
5×3=15;
16÷4=4
4×4=16
15<16,正方形的面积大。
故答案为:正确。
假设周长相等的长方形和正方形的周长都是16,依据周长分别计算出面积,则周长相等的长方形和正方形,正方形的面积大。
13.正确
解:长方形木条框,拉住它的两个对角,可以变成一个平行四边形,拉出的平行四边形和原来的长方形周长没变,面积变了,此题说法正确。
故答案为:正确。
把一个长方形的框架拉成一个平行四边形后,四条边的长度没变,则四条边的长度和不变,即它的周长不变;
平行四边形的高比长方形的宽小了,底没变,由长方形和平行四边形的面积公式可知,这个平行四边形的面积与原长方形面积相比就变小了。
14.正确
解:时光一去不复返,这是一定的,原题说法正确。
故答案为:正确
时光过去就不会再回来,所以时光是不可能复返的,由此判断即可。
15.错误
解:两个平行四边形等底等高,但是对应的另外一组对边不一定相等,所以这两个平行四边形不一定相同,原题说法错误.
故答案为:错误
平行四边形是两组对边分别平行且相等的四边形,两个等底等高的平行四边形的形状是不一定相同的.
16.;;8
解:8÷20= ;
的分数单位是 ;
2- =,表示有8个 ,所以再添上8个这样的分数单位就是最小的质数。
故答案为: ; ;8。
根据分数的意义,分数单位是指把单位“1”平均分成若干份,表示其中的一份的数叫做分数单位,题中分母表示平均分成的份数,分子表示取走的份数。最小的质数是2。
17.
18.;3
解:0~1被平均分成5份,每份是;A点表示,
最小的质数是2,2=,-=;
直线上的A点用分数表示是,再添上3个它的分数单位后就变成最小的质数。
故答案为:;3。
一个分数的分数单位就是分母分之一,它有分子个这样的分数单位。
19.250;;24
解:350×=250(m),
2÷5=,
30÷(1+25%)
=30÷1.25
=24(m2);
故答案为:250;;24。
根据求一个数的几分之几是多少,用乘法计算;已知一个数的几分之几是多少,求这个数,用除法计算;已知比一个数多百分之几,求这个数,用除法计算即可。
20.一箱苹果;4;3;
解:“一箱苹果吃去了。”这是把一箱苹果看做单位“1”,把它平均分成了4份,吃去的苹果有这样的3份,由此可以推出剩下这箱苹果的。
故答案为:一箱苹果;4;3;。
根据题意可知,一箱苹果的总质量为单位“1”,将其平均分成4份,吃了其中的3份,还剩下1份,即剩下这箱苹果的 ,据此解答即可。
21.<;=;<;>
解:5.18×0.99<5.18,5.18÷0.99 >5.18,所以5.18×0.99<5.18÷0.99
0.89÷0.5=0.89×2
=0.666......,所以0.66<
=,=,所以 >
故答案为:<;=;<;>。
第一空:一个非0数乘小于1的数,积小于这个数;一个非0数除以小于1的数,商大于这个数;据此解答;
第二空:除以一个数,等于乘这个数的倒数;
第三空:先把分数化为小数,再比较大小;
第四空:分子是1的分数,分母小的分子大。
22.10;21;12;0.6
解:3÷5==;3÷5=(3×7)÷(5×7)=21÷35;3÷5==;
所以3÷5==21÷35==0.6。
故答案为:10;21;12;0.6。
被除数相当于分子,除数相当于分母。根据分数与除法的关系确定分母、被除数或分子。用小数表示3除以5的商。
23.98.25
解:三角形面积为:底×高2
高为89.2511.9=7.5m
蔬菜的种植面积 =平行四边形的面积 - 三角形的面积。
平行四边形面积:257.5=187.5
蔬菜的种植面积 =187.5-89.25=98.25
故答案为:98.25
题目中给出了一个平行四边形劳动基地,其中三角形区域种植农作物,梯形区域种植蔬菜。
已知农作物的种植面积是平方米,梯形(蔬菜)的面积 = 平行四边形的面积 - 三角形的面积。
24.7;3
解:假设全是自行车,三轮车的辆数:(27-10×2)÷(3-2)=7(辆),自行车的辆数:10-7=3(辆)。
故答案为:7;3。
假设全是自行车,三轮车的辆数=(轮子的个数-每辆自行车有轮子的个数×2)÷每辆三轮车轮子的个数比自行车多的个数,自行车的辆数=一共的辆数-三轮车的辆数。
25.6
解:4.5÷0.8≈6(个)。
故答案为:6。
至少需要这种玻璃瓶的个数=花生油的总质量÷平均每个玻璃瓶装花生油的质量,计算的结果用“进一法” 。
26.
8.1×100=810 0.25×6=1.5 0.05×0.04 =0.002 0.3×50=15
0.72÷8=0.09 2.8÷100=0.028 0.3÷0.03=10 1.4÷0.04=35
小数乘法,先按整数乘法算出积,再看因数中一共有几位小数,就从积的右边起数出几位,点上小数点;
除数是小数的除法,先移动除数的小数点,使它变成整数,除数的小数点向右移动几位,被除数的小数点也向右移动几位,然后按照除数是整数的除法进行计算;
一个非0的数乘(除以)10,小数点向右(左)移动一位;一个非0的数乘(除以)100,小数点向右(左)移动两位;一个非0的数乘(除以)1000,小数点向右(左)移动三位;……
27.15;0.9;140
28.解:
=34.5÷1.5
=23
=9.86÷1.7
=5.8
=20-(3.2+6.8)
=20-10
=10
=8.4×(4.9+5.1)
=8.4×10
=84
=61+3.05
=64.05
=2.6÷(0.25×0.4)
=2.6÷0.1
=26
第一题:根据乘除法运算顺序进行计算。
第二题:根据四则混合运算顺序进行计算。
第三题:根据连续减去两个数等于减去这两个数的和进行简便计算。
第四题:根据乘法分配律进行简便计算。
第五题:根据四则混合运算顺序进行计算。
第六题:根据连续除以两个数等于除以这两个数的乘积进行简便计算。
29.(1)解:24×8+24×10÷2
=192+240÷2
=192+120
=312(m2)
(2)解:
12×10+(12+20)×(16-10)÷2
=120+32×6÷2
=120+96
=216(平方厘米)
(1)三角形的面积=三角形的底×底边上的高÷2;平行四边形的面积=平行四边形的底×底边上的高;三角形面积+平行四边形面积=图形的面积;
(2)梯形的面积=(梯形的上底+梯形的下底)×梯形的高÷2;长方形的面积=长×宽;梯形面积+长方形面积=图形的面积。
30.(1)解:如图⑤:
(2)解:如图⑥:
(3)解:如图⑦:
(4)解:如图⑧:
(5)(4,2)
解:(5)点O的位置用数对表示为 (4,2) 。
故答案为:(5) (4,2) 。
(1)平移画法:先把图形中的关键点都按题干要求的方向和格数移动,然后再连接各点;
(2)补全轴对称图形方法:根据对称点到对称轴的距离相等,找出各个关键点的对称点,然后再连线;
(3)旋转画法:旋转后图形的位置改变,转动的中心点、形状、大小不变。因此画图时,先弄清楚旋转的方向和角度,找准关键线段旋转后的位置,据此作图即可;
(4)图④的长和宽的格数都乘以2,就是按2:1放大后的图形;
(5)数对的表示方法:先列后行。
31.解:
答:第一次投放的益生菌是两次投放总和的。
32.解:(0.3×0.3)×72÷(0.4×0.4)≈41(块)
答: 需要41块
33.解:设分别花了元购买了甲乙丙三种糖果。
因此成本总额为(元)
则甲乙丙数量总共为(千克)
什锦糖每千克定价为(元)
答:这种什锦糖每千克定价 14.4元。
因为“甲、乙、丙三种糖果每千克的价格分别是10元、12元、15元,并且分别花同样多的钱,购进甲、乙、丙三种不同的糖果”,此时如果从数量角度来设未知数,则未知数就会有三个,因此从购进成本角度来设未知数则会简便。首先找到10、12、15的最小公倍数60,因此设分别花了元购买了甲乙丙三种糖果,这样总共成本就是180x元。对应的甲乙丙数量也就可以求出,总数量也就可以求出,为15x千克。根据公式“销售定价×数量=成本总额×(1+利润率)”,因此销售定价=,代入计算即可。
34.解:如图:
连接BD,因为EB=2AE,所以三角形BDE的面积是三角形ADE的面积的2倍,三角形ADB的面积是三角形ADE的面积的1+2=3倍,平行四边形的面积是三角形ADE的面积的3×2=6倍,梯形BCDE的面积是三角形ADE面积的(6-1)倍;
所以梯形BCDE的面积是:10×(6-1)=50(平方厘米)
答:梯形BCDE的面积是50平方厘米。
连接BD,因为EB=2AE,等高的三角形的面积比等于底的比,所以三角形BDE的面积是三角形ADE的面积的2倍,三角形BDE与三角形ADE的面积和正好是平行四边形面积的一半,平行四边形面积的一半是三角形ADE的面积的3倍,所以平行四边形的面积是三角形ADE的面积的6倍,梯形的面积是三角形ADE的面积的(6-1)倍,据此用ADE的面积乘(6-1)就是梯形的面积。
35.(1)解:国道花费:66×8=528(元)
高速花费:57×8+270
=456+270
=726(元)
726>528
答:选择国道路线更划算。
(2)解:运输距离:(66-57)÷3x100
=9÷3×100
=3×100
=300(公里)
高速用时:300÷100=3(小时)
3x60=180(分钟)
国道用时:300÷60=5(小时)
需休息的次数:5÷4=1(次)……1(小时)
加上疲劳驾驶的休息时间:5x60+20=320(分钟)
两种方式送达的时间差:320-180=140(分钟)
答:两种不同方式将货物送达的时间差是140 分钟。
(1)根据每升油的单价×油耗=一共需要的钱数,分别计算出走国道和走高速的费用,再对比,哪种钱越少,越划算;
(2)根据题意可知,先求出运输的距离,然后分别求出高速用的时间和国道用的时间,根据条件“ 驾驶员连续驾驶4小时机动车,至少需停车休息20分钟”求出需要休息的次数,然后求出加上疲劳驾驶的休息时间,最后用减法求出两种方式送达的时间差,据此列式解答。
20224-2025学年五年级上册期末模拟卷(北师大版)
数学
考试范围:五上全册 考试时间:100分钟 分值:100分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
一、精挑细选,慎重选择。(请在答题卡相应位置作答)(共9分)
1.淘气一个月看完一本书,这个月上旬,他看完了总页数的,中旬看了剩下的,中旬看了总页数的( )
A. B. C. D.
2.要得到左面的图案,应将正方形纸按( )的方式剪掉涂色部分。
A. B. C.
3.下列说法中,正确的有( )个。
①0是最小的自然数
②一个数最少有两个因数
③是质数的一定是奇数,是偶数的一定是合数
④任意三个连续自然数的和一定是3的倍数
A.1 B.2 C.3 D.4
4.哥德巴赫猜想:“任意一个大于2的偶数都可以表示成两个质数的和”。下面的算式中符合这个猜想的是( )。
A.10=2+8 B.16=3+13 C.14=5+9 D.8=7+1
5.如图,把大长方形的面积看成单位“1”,则斜线部分的面积用算式( )表示。
A. B. C.
6.下边的算式没有算完,根据算式,商是( )。
A.0.68 B. C. D.无法确定
7.某市高新区规划了一个正方形的居民活动中心,周长是1600米,它的面积是( )。
A.1600公顷 B.16000平方米 C.16公顷
8.妙妙和聪聪玩拼数游戏,在如图四张卡片中,任意选三张组成三位数,在这些数中同时是2、3和5的倍数的有( )个。
A.2 B.4 C.6 D.8
9.桌子上摆着10张卡片,上面写着1至10十个数字,任意抽取一张卡片,笑笑设计以下游戏规则,哪一种规则不公平 ( )
A.抽到奇数笑笑赢,抽到偶数妙想赢。
B.抽到数字大于5的卡片笑笑赢,抽到数字小于5的卡片妙想赢。
C.抽到有1、3、4、7、8这五个数字中任意一个数字的卡片则笑笑赢,抽到其它卡片则妙想赢。
D.如果抽到的卡片上数字是1或者质数,笑笑赢;如果抽到的卡片上数字是合数,妙想赢。
二、火眼金睛,细心裁判。(共6分)
10.在除法中,如果除不尽则商一定是无限循环小数。 ( )
11.两个质数相乘的积一定是偶数。( )
12.周长相等的长方形和正方形,面积相比,正方形的面积大些。( )
13.一个长方形的木条框,拉住它的两个对角,使它变成一个平行四边形,拉出的平行四边形和原来的长方形周长没变,面积变了。( )
14.时光一去不复返。
15.两个等底等高的平行四边形,形状一定相同。
三、欢乐填空,对号入座。(把答案填到答题卡相应位置上)(共23分)。
16.古诗“春水春池满,春时春草生。春人饮春酒,春鸟弄春声。”在这首诗中出现次数最多的一个字占全诗总字数的 ,这个分数的分数单位是 ,再添上 个这样的分数单位就是最小的质数。
17.周末奇奇用爸爸的围棋棋子摆放了一系列的图形,这些图形蕴含一定的规律。
请观察以上各图,在方框中按规律补齐。
18.下图中,直线上的A点用分数表示是 ,再添上 个它的分数单位后就变成最小的质数。
19.350 m 的 是 的 是 比 多 。
20.“一箱苹果吃去了。”这是把 看做单位“1”,把它平均分成了 份,吃去的苹果有这样的 份,由此可以推出剩下这箱苹果的 。
21.在横线上填上“>”、“<”或“=”。
5.18×0.99 5.18÷0.99 0.89÷0.5 0.89×2
0.66
22.3÷5= = ÷35= = (填小数)
23.某小学开展以“学劳动、会劳动、爱劳动”为主题的多彩劳动课堂。五年级分到一块平行四边形劳动基地,如图,其中梯形区域种植蔬菜,三角形区域种植农作物。已知农作物的种植面积是89.25m2,那么蔬菜的种植面积是 m2。
24.自行车和三轮车一共有10辆,数一数它们的轮子有27个。三轮车有 辆,自行车有 辆。
25. 一种玻璃瓶可以装 0.8 千克花生油。现有 4.5 千克花生油, 用这种玻璃瓶来装完,至少需要这种玻璃瓶 个。
四、耐心审题,巧思妙算。(共32分)
26.直接写出得数。
8.1×100= 0.25×6= 0.05×0.04 = 0.3×50=
0.72÷8= 2.8÷100= 0.3÷0.03= 1.4÷0.04=
竖式计算。
6.3÷0.42= 1.25×0.72= 23.8÷0.17=
28.脱式计算、能简算的要简算。
29.计算下面各图形的面积。
(1)
(2)
五、仔细观察,认真操作。(共6分)
30.按要求画一画,填﹣填。
(1)画出图①向右平移5格后的图形。
(2)以直线l为对称轴,画出轴对称图形图②的另一半。
(3)画出图③绕点O沿顺时针方向旋转90°后的图形。
(4)画出图④按2:1放大后的图形。
(5)点A的位置用数对(5,10)表示,则点O的位置用数对表示为 。
六、走进生活,解决问题。(共24分)
31.(教参 P147样题13变式)将益生菌混合饲料投喂给虾摄食。水产养虾益生菌可以调节并稳定水质。试验人员第一次向虾沟里投放了980克水产养虾益生菌,第二次投放的比第一次少120克,第一次投放的益生菌是两次投放总和的几分之几
小莉的房间要用方砖铺地,如果用边长是0.3米的方砖,那么需要72块;如果改用边长是0.4米的方砖,那么需要多少块? (结合实际取近似数)
某商店分别花同样多的钱,购进甲、乙、丙三种不同的糖果。已知甲、乙、丙三种糖果每千克的价格分别是10元、12元、15元。如果把这三种糖果混合成什锦糖,按20%的利润定价,那么这种什锦糖每千克定价多少元
34.如下图,DE把平行四边形 ABCD分成了一个三角形和一个梯形,且EB=2AE。已知三角形ADE 的面积是10cm2, 则 梯 形BCDE 的面积是( ) cm2 。请写出主要过程。
35. 小货车司机王叔叔需要运送一批家具,通过国道或者高速进行运输的距离相同,根据往常的经验,走国道油耗66升,走高速油耗57升。高速需收取过路费270元。
(1)选择哪条路线更划算 (油价8元/升)
(2)已知本次运输中,该车走国道每百公里油耗比高速多3升,国道限速60公里/小时,高速的限速是100公里/小时,王叔叔在不超速和不违反疲劳驾驶规定的情况下按最大速度行驶,选择两种方式将货物送达的时间差是多少分钟
根据相关观定:驾驶员连续驾驶4小时机动车,至少需停车休息20分钟,否则将构成疲劳驾驶
答案解析部分
1.A
解:(1-)×
=×
=。
故答案为:A。
淘气中旬看了总页数分率=(1-上旬看的分率) ×。
2.A
解:应将正方形纸按 的方式剪掉涂色部分。
故答案为:A。
按 的方式剪掉涂色部分后就得到一个正六边形。
3.B
解:①自然数是大于或等于0的整数,所以0是最小的自然数,此说法正确;
②1只含有1一个因数,此说法错误;
③2是质数但是偶数,此说法错误;
④设三个连续自然数中的第一个为a,则三个连续自然数的和为a+(a+1)+(a+2)=3a+3=3×(a+1),所以任意三个连续自然数的和一定是3的倍数,此说法正确。
故答案为:B。
我们在数物体的时候,用来表示物体个数的0,1,2,3……叫做自然数;
1只有1个因数,就是它自己;
能被2整除的数叫做偶数;不能被2整除的数叫做奇数;
一个数,如果只有1和它本身两个因数,这样的数叫做质数;
任意两个相邻自然数的差是1,任意三个连续自然数的和一定是3的倍数。
4.B
解:选项A, 10=2+8,10是偶数,2是质数,但是8是合数,与题意不符;
选项B, 16=3+13,16是偶数,3和13都是质数,与题意相符;
选项C, 14=5+9,14是偶数,5是质数,9是合数,与题意不符;
选项D, 8=7+1,8是偶数,7是质数,1既不是质数也不是合数,与题意不符。
故答案为:B。
能被2整除的数叫做偶数;不能被2整除的数叫做奇数;
一个数,如果只有1和它本身两个因数,这样的数叫做质数;分别判断各选项的数据即可。
5.B
解:4份涂色,表示,1份涂斜线,表示,所以算式是 。
股答案为:B
把大长方形的面积看成单位“1”,把它平均分成5份,每份是它的,其中4份涂色,表示;再把涂色部分看作单位“1”,把它平均分成3份,每份是它的,其中1份涂斜线,表示,求斜线部分的面积就是求的是多少,用乘法 计算。
6.B
解:观察下面竖式发现余数8已经开始重复出现,也就是商后面的数会重复出现,“0.68”中的末尾是8,8会重复出现,所以商是。
故答案为:B。
循环小数是从小数部分的某一位起,一个数字或几个数字,依次不断地重复出现的小数。一个循环小数的小数部分,依次不断重复出现的数字,就是这个循环小数的循环节。写循环小数时,可以只写第一个循环节,并在这个循环节的首位和末尾数字上面各记一个圆点。
7.C
解:1600÷4=400(米)
400×400=160000(平方米)
160000平方米÷10000=16公顷
它的面积是16公顷
故答案为:C。
正方形的周长÷4=正方形的边长,正方形的边长×正方形的边长=正方形的面积,平方米÷10000=公顷。
8.B
解:既是2的倍数又是5的倍数的三位数末位是0,各个数位上的数字之和是3的倍数的数,就是3的倍数,所以百位上的数字和十位上的数字之和要是3的倍数,4+5=9=3×3, 5+7=12=3×4, 4+7=11, 11不是3的倍数,所以任意选三张组成三位数,在这些数中同时是2、3 和5的倍数的是 450、540、570、750, 共4个。
故答案为:B。
同时是2、3、5的倍数的数的特征:一个数各个数位上的数字之和是3的倍数,个位是0,据此解答。
9.B
解:选项A,1至10十个数字,有5个奇数,5个偶数,任意抽取一张卡片,抽到奇数和偶数的可能性相等,游戏规则是公平的;
选项B,大于5的卡片有6、7、8、9、10,小于5的卡片有1、2、3、4,任意抽取一张卡片,抽到大于5的可能性大,游戏规则不公平;
选项C,一共有10个数字,抽到有1、3、4、7、8这五个数字中任意一个数字的卡片则笑笑赢,抽到其它卡片则妙想赢,此游戏规则公平;
选项D,从1到10十个数字中,1和质数有2、3、5、7共5个数,剩下5个是合数,如果抽到的卡片上数字是1或者质数,笑笑赢;如果抽到的卡片上数字是合数,妙想赢,此游戏规则公平。
故答案为:B。
此题主要考查了游戏规则的公平性,1至10十个数字,奇数有:1、3、5、7、9,偶数有:2、4、6、8、10;质数有2、3、5、7,合数有4、6、8、9、10;大于5的数字有6、7、8、9、10,小于5的数字有1、2、3、4,分别对比抽到情况的可能性,可能性相等,游戏规则公平,否则,不公平。
10.错误
解:在除法中,如果除不尽,商可能是循环小数,也可能是无限不循环小数,原题说法错误。
故答案为:错误。
小数分为有限小数和无限小数,无限小数分为无限不循环小数和循环小数,据此判断。
11.错误
解:假设这两个质数分别为3和5,那么3×5=15,15是奇数;
故答案为:错误。
质数×质数=合数,但不一定是偶数。
12.正确
解:假设长方形和正方形的周长是16。
(5+3)×2
=8×2
=16
5×3=15;
16÷4=4
4×4=16
15<16,正方形的面积大。
故答案为:正确。
假设周长相等的长方形和正方形的周长都是16,依据周长分别计算出面积,则周长相等的长方形和正方形,正方形的面积大。
13.正确
解:长方形木条框,拉住它的两个对角,可以变成一个平行四边形,拉出的平行四边形和原来的长方形周长没变,面积变了,此题说法正确。
故答案为:正确。
把一个长方形的框架拉成一个平行四边形后,四条边的长度没变,则四条边的长度和不变,即它的周长不变;
平行四边形的高比长方形的宽小了,底没变,由长方形和平行四边形的面积公式可知,这个平行四边形的面积与原长方形面积相比就变小了。
14.正确
解:时光一去不复返,这是一定的,原题说法正确。
故答案为:正确
时光过去就不会再回来,所以时光是不可能复返的,由此判断即可。
15.错误
解:两个平行四边形等底等高,但是对应的另外一组对边不一定相等,所以这两个平行四边形不一定相同,原题说法错误.
故答案为:错误
平行四边形是两组对边分别平行且相等的四边形,两个等底等高的平行四边形的形状是不一定相同的.
16.;;8
解:8÷20= ;
的分数单位是 ;
2- =,表示有8个 ,所以再添上8个这样的分数单位就是最小的质数。
故答案为: ; ;8。
根据分数的意义,分数单位是指把单位“1”平均分成若干份,表示其中的一份的数叫做分数单位,题中分母表示平均分成的份数,分子表示取走的份数。最小的质数是2。
17.
18.;3
解:0~1被平均分成5份,每份是;A点表示,
最小的质数是2,2=,-=;
直线上的A点用分数表示是,再添上3个它的分数单位后就变成最小的质数。
故答案为:;3。
一个分数的分数单位就是分母分之一,它有分子个这样的分数单位。
19.250;;24
解:350×=250(m),
2÷5=,
30÷(1+25%)
=30÷1.25
=24(m2);
故答案为:250;;24。
根据求一个数的几分之几是多少,用乘法计算;已知一个数的几分之几是多少,求这个数,用除法计算;已知比一个数多百分之几,求这个数,用除法计算即可。
20.一箱苹果;4;3;
解:“一箱苹果吃去了。”这是把一箱苹果看做单位“1”,把它平均分成了4份,吃去的苹果有这样的3份,由此可以推出剩下这箱苹果的。
故答案为:一箱苹果;4;3;。
根据题意可知,一箱苹果的总质量为单位“1”,将其平均分成4份,吃了其中的3份,还剩下1份,即剩下这箱苹果的 ,据此解答即可。
21.<;=;<;>
解:5.18×0.99<5.18,5.18÷0.99 >5.18,所以5.18×0.99<5.18÷0.99
0.89÷0.5=0.89×2
=0.666......,所以0.66<
=,=,所以 >
故答案为:<;=;<;>。
第一空:一个非0数乘小于1的数,积小于这个数;一个非0数除以小于1的数,商大于这个数;据此解答;
第二空:除以一个数,等于乘这个数的倒数;
第三空:先把分数化为小数,再比较大小;
第四空:分子是1的分数,分母小的分子大。
22.10;21;12;0.6
解:3÷5==;3÷5=(3×7)÷(5×7)=21÷35;3÷5==;
所以3÷5==21÷35==0.6。
故答案为:10;21;12;0.6。
被除数相当于分子,除数相当于分母。根据分数与除法的关系确定分母、被除数或分子。用小数表示3除以5的商。
23.98.25
解:三角形面积为:底×高2
高为89.2511.9=7.5m
蔬菜的种植面积 =平行四边形的面积 - 三角形的面积。
平行四边形面积:257.5=187.5
蔬菜的种植面积 =187.5-89.25=98.25
故答案为:98.25
题目中给出了一个平行四边形劳动基地,其中三角形区域种植农作物,梯形区域种植蔬菜。
已知农作物的种植面积是平方米,梯形(蔬菜)的面积 = 平行四边形的面积 - 三角形的面积。
24.7;3
解:假设全是自行车,三轮车的辆数:(27-10×2)÷(3-2)=7(辆),自行车的辆数:10-7=3(辆)。
故答案为:7;3。
假设全是自行车,三轮车的辆数=(轮子的个数-每辆自行车有轮子的个数×2)÷每辆三轮车轮子的个数比自行车多的个数,自行车的辆数=一共的辆数-三轮车的辆数。
25.6
解:4.5÷0.8≈6(个)。
故答案为:6。
至少需要这种玻璃瓶的个数=花生油的总质量÷平均每个玻璃瓶装花生油的质量,计算的结果用“进一法” 。
26.
8.1×100=810 0.25×6=1.5 0.05×0.04 =0.002 0.3×50=15
0.72÷8=0.09 2.8÷100=0.028 0.3÷0.03=10 1.4÷0.04=35
小数乘法,先按整数乘法算出积,再看因数中一共有几位小数,就从积的右边起数出几位,点上小数点;
除数是小数的除法,先移动除数的小数点,使它变成整数,除数的小数点向右移动几位,被除数的小数点也向右移动几位,然后按照除数是整数的除法进行计算;
一个非0的数乘(除以)10,小数点向右(左)移动一位;一个非0的数乘(除以)100,小数点向右(左)移动两位;一个非0的数乘(除以)1000,小数点向右(左)移动三位;……
27.15;0.9;140
28.解:
=34.5÷1.5
=23
=9.86÷1.7
=5.8
=20-(3.2+6.8)
=20-10
=10
=8.4×(4.9+5.1)
=8.4×10
=84
=61+3.05
=64.05
=2.6÷(0.25×0.4)
=2.6÷0.1
=26
第一题:根据乘除法运算顺序进行计算。
第二题:根据四则混合运算顺序进行计算。
第三题:根据连续减去两个数等于减去这两个数的和进行简便计算。
第四题:根据乘法分配律进行简便计算。
第五题:根据四则混合运算顺序进行计算。
第六题:根据连续除以两个数等于除以这两个数的乘积进行简便计算。
29.(1)解:24×8+24×10÷2
=192+240÷2
=192+120
=312(m2)
(2)解:
12×10+(12+20)×(16-10)÷2
=120+32×6÷2
=120+96
=216(平方厘米)
(1)三角形的面积=三角形的底×底边上的高÷2;平行四边形的面积=平行四边形的底×底边上的高;三角形面积+平行四边形面积=图形的面积;
(2)梯形的面积=(梯形的上底+梯形的下底)×梯形的高÷2;长方形的面积=长×宽;梯形面积+长方形面积=图形的面积。
30.(1)解:如图⑤:
(2)解:如图⑥:
(3)解:如图⑦:
(4)解:如图⑧:
(5)(4,2)
解:(5)点O的位置用数对表示为 (4,2) 。
故答案为:(5) (4,2) 。
(1)平移画法:先把图形中的关键点都按题干要求的方向和格数移动,然后再连接各点;
(2)补全轴对称图形方法:根据对称点到对称轴的距离相等,找出各个关键点的对称点,然后再连线;
(3)旋转画法:旋转后图形的位置改变,转动的中心点、形状、大小不变。因此画图时,先弄清楚旋转的方向和角度,找准关键线段旋转后的位置,据此作图即可;
(4)图④的长和宽的格数都乘以2,就是按2:1放大后的图形;
(5)数对的表示方法:先列后行。
31.解:
答:第一次投放的益生菌是两次投放总和的。
32.解:(0.3×0.3)×72÷(0.4×0.4)≈41(块)
答: 需要41块
33.解:设分别花了元购买了甲乙丙三种糖果。
因此成本总额为(元)
则甲乙丙数量总共为(千克)
什锦糖每千克定价为(元)
答:这种什锦糖每千克定价 14.4元。
因为“甲、乙、丙三种糖果每千克的价格分别是10元、12元、15元,并且分别花同样多的钱,购进甲、乙、丙三种不同的糖果”,此时如果从数量角度来设未知数,则未知数就会有三个,因此从购进成本角度来设未知数则会简便。首先找到10、12、15的最小公倍数60,因此设分别花了元购买了甲乙丙三种糖果,这样总共成本就是180x元。对应的甲乙丙数量也就可以求出,总数量也就可以求出,为15x千克。根据公式“销售定价×数量=成本总额×(1+利润率)”,因此销售定价=,代入计算即可。
34.解:如图:
连接BD,因为EB=2AE,所以三角形BDE的面积是三角形ADE的面积的2倍,三角形ADB的面积是三角形ADE的面积的1+2=3倍,平行四边形的面积是三角形ADE的面积的3×2=6倍,梯形BCDE的面积是三角形ADE面积的(6-1)倍;
所以梯形BCDE的面积是:10×(6-1)=50(平方厘米)
答:梯形BCDE的面积是50平方厘米。
连接BD,因为EB=2AE,等高的三角形的面积比等于底的比,所以三角形BDE的面积是三角形ADE的面积的2倍,三角形BDE与三角形ADE的面积和正好是平行四边形面积的一半,平行四边形面积的一半是三角形ADE的面积的3倍,所以平行四边形的面积是三角形ADE的面积的6倍,梯形的面积是三角形ADE的面积的(6-1)倍,据此用ADE的面积乘(6-1)就是梯形的面积。
35.(1)解:国道花费:66×8=528(元)
高速花费:57×8+270
=456+270
=726(元)
726>528
答:选择国道路线更划算。
(2)解:运输距离:(66-57)÷3x100
=9÷3×100
=3×100
=300(公里)
高速用时:300÷100=3(小时)
3x60=180(分钟)
国道用时:300÷60=5(小时)
需休息的次数:5÷4=1(次)……1(小时)
加上疲劳驾驶的休息时间:5x60+20=320(分钟)
两种方式送达的时间差:320-180=140(分钟)
答:两种不同方式将货物送达的时间差是140 分钟。
(1)根据每升油的单价×油耗=一共需要的钱数,分别计算出走国道和走高速的费用,再对比,哪种钱越少,越划算;
(2)根据题意可知,先求出运输的距离,然后分别求出高速用的时间和国道用的时间,根据条件“ 驾驶员连续驾驶4小时机动车,至少需停车休息20分钟”求出需要休息的次数,然后求出加上疲劳驾驶的休息时间,最后用减法求出两种方式送达的时间差,据此列式解答。
同课章节目录
