2024-2025学年沪教版六年级数学上册期末模拟卷(含答案)
文档属性
| 名称 | 2024-2025学年沪教版六年级数学上册期末模拟卷(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 231.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-09 00:00:00 | ||
图片预览




文档简介
保密★启用前
20224-2025学年六年级上册期末模拟卷(沪教版)
数学
考试范围:六上全册 考试时间:100分钟 分值:100分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
一、填空题(共24分)
1.分解素因数:18= 。
2. 数的倒数是 .
3.在,,,中最大的数是 .
4.求比值: .
5.如果,那a与b成 比例,比值是 .
6.饮料厂从一批产品中抽查了40瓶饮料,其中8瓶不合格,合格率是 .
7.是 的, 比多.
8.在物理课上,某实验的电路图如图所示,其中S1,S2,S3表示电路的开关,L表示小灯泡,R为保护电阻.若闭合开关S1,S2,S3中的任意两个,则小灯泡L发光的概率为 .
9.如图,在矩形ABCD中,AB=4,AD=6,P是边BC上一动点(不与点B、C重合).连接AP,过点D作DE⊥PA,垂足为E,则线段BE长的最小值为 .
10.一批零件,原计划按分配给师徒两人加工,结果师傅加工1200个,超过分配任务的,而徒弟因病只完成了他原定任务的,徒弟实际加工了 个.
11.如图,一枚圆形古钱币的中间是一个正方形孔,已知圆的直径与正方形的对角线之比为3∶1,则圆的面积约为正方形面积的 倍.(精确到个位)
12.有大小两个圆,大圆直径是小圆直径的2.5倍,大圆的周长与小圆的周长比是 ,面积比是 .
二、选择题(共12分)
13.古希腊数学家欧几里得证明了素数也就是质数有无限多个,提出少量素数可以写成“”的形式,这里的也是一个素数千百年来一直吸引着众多的数学家对它进行研究和探索,世纪法国著名数学家马林梅森是其中成果较为卓著的一位,因此后人将“”型的素数称为梅森素数下面个数中,( )是梅森素数注:表示个相乘
A. B. C. D.
14.(第十九届“五羊杯”初中数学竞赛七年级)S==( ).(其中[x]表示不超过x的最大整数)
A.2006000 B.2006001 C.2007003 D.4014006
15.下列式子中,正确运用分数基本性质的是( )
A. B. C. D.
16.的三角之比是,则是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.无法确定
17.若圆的直径和正方形的边长都是,则圆的周长( )正方形的周长.
A.大于 B.等于 C.小于 D.不能确定
18.如图,边长为2的正方形的中心与半径为2的的圆心重合,,分别是,的延长线与的交点,则图中阴影部分的面积为( )
A. B. C. D.
三、简答题(共30分)
19.用简便方法计算.
(1)
(4)
20.直接写得数
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
(9)
(10)
21.计算题:
①;
②求未知数:;
③;
④.
22.求未知数x.
(1);
(2).
23.化简比.
(1)
(2)小时分:小时分
(3)升:升毫升
学校原有足球、篮球一共个,足球与篮球个数之比是,后来又买回一些足球,这时足球与两种球总个数之比是,求又买回多少个足球.
四、解答题(共26分)
25.求阴影部分的周长及面积.(结果保留)
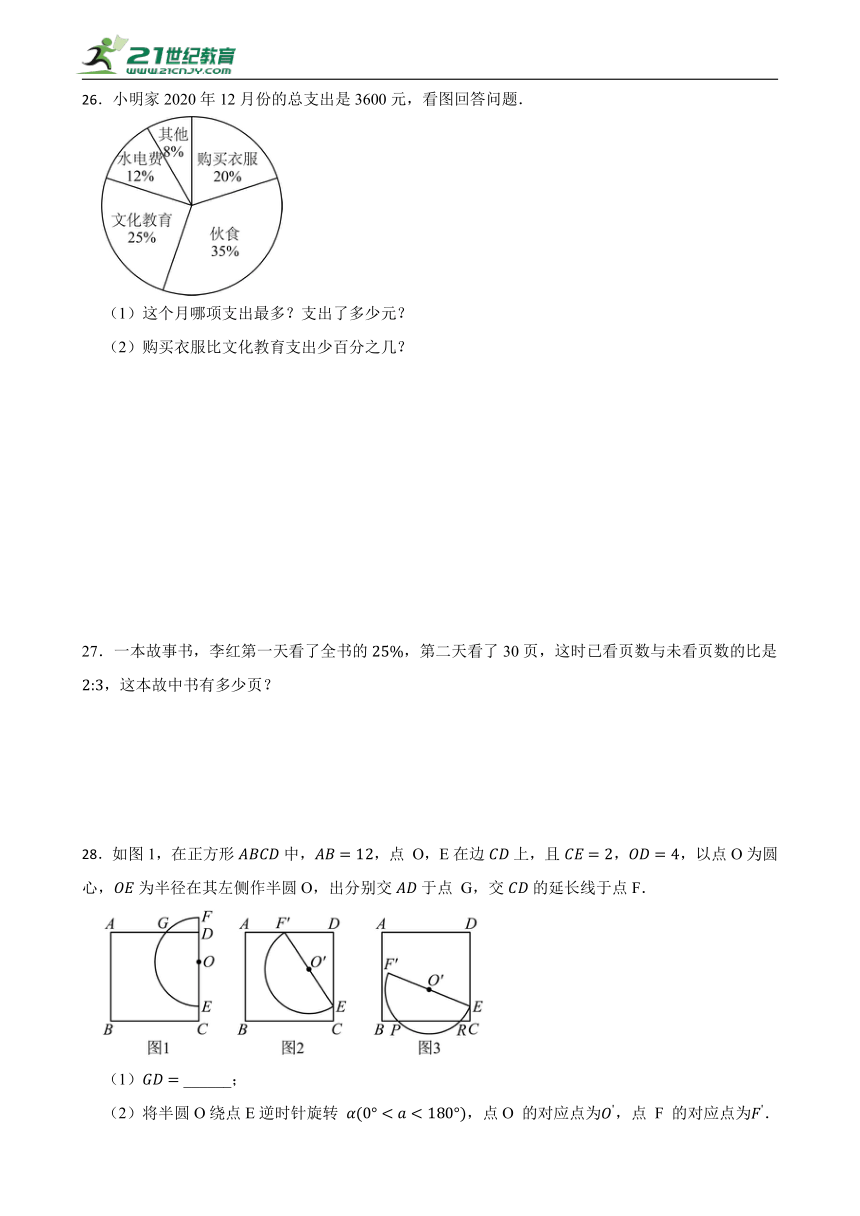
26.小明家2020年12月份的总支出是3600元,看图回答问题.
(1)这个月哪项支出最多?支出了多少元?
(2)购买衣服比文化教育支出少百分之几?
一本故事书,李红第一天看了全书的,第二天看了30页,这时已看页数与未看页数的比是,这本故中书有多少页?
28.如图1,在正方形中,,点 O,E在边上,且,,以点O为圆心,为半径在其左侧作半圆O,出分别交于点 G,交的延长线于点F.
(1) ______;
(2)将半圆O绕点E逆时针旋转 ,点O 的对应点为,点 F 的对应点为.
①如图2,若M为半圆上一点,当点落在边上时,求点M到线段的最短距离;
②如图3,当半圆交于P,R两点时,若 ,求此时半圆与正方形重叠部分的面积;
③当半圆与正方形的边相切时,设切点为N,直接写出的值.
五、综合题(共8分)
29.如图所示是一个几何体的表面展开图.
(1)该几何体的名称是 ,其底面半径为 .
(2)根据图中所给信息,求该几何体的侧面积和体积(结果保留)
答案解析部分
1.2×3×3
解:18=2×3×3。
故答案为:2×3×3。
分解素因数,要从最小的素数除起,一直除到结果为素数为止。
2.-3
解:由题意可得:
的倒数是-3
故答案为:-3
根据代数的定义即可求出答案.
3.
解:∵,
∴
∴所以最大的数是
故答案为:.
先把,,然后得出:∴,而,因此可得:
.
4.
5.正;
6.80%
解:(40-8)÷40=0.8=80%.
故答案为:80%.
先求出合格的瓶数,用合格瓶数除以40即可.
7.;
根据题意可得:6÷=10;2×(1+50%)=3,
故答案为:10;3.
根据分数乘除法列出算式求解即可.
8.
解:列表如下:
S1 S2 S3
S1 —— (S1,S2) (S1,S3)
S2 (S2,S1) —— (S2,S3)
S3 (S3,S1) (S3,S2) ——
共有6中可能的情况,当闭合S1、S3 时灯泡才亮,
∴则小灯泡L发光的概率为.
故答案为:.
用列表法列出所有的情况,当闭合S1、S3 时灯泡才亮,所以情况有2种,从而根据概率公式即可得出小灯泡L发光的概率为.
9.2.
10.360
解:师傅的任务(个)
徒弟的任务(个)
徒弟实际加工(个)
答:徒弟实际加工了360个.
故答案为:360.
先用师傅实际加工零件的个数除以其占比求出师傅的任务,进而可求出徒弟的任务,再用徒弟的任务乘以60%,可求出徒弟实际加工的个数.
11.14
解:如图
由题意得AC与EF共线
∵圆的直径与正方形的对角线之比为3:1
∴EF:AC=3:1
∴OE:OA=3:1
设OE=3x,OA= x
在正方形ABCD中
由勾股定理得:AD=x
∴圆的面积为:π×(3x)2=9πx2
正方形的面积为(x)2=2 x2
∴9πx2÷2 x2=≈14
故答案为:14
如图,由圆的直径与正方形的对角线之比为3:1,可得EF:AC=3:1,即得OE:OA=3:1;设OE=3x,OA= x,由勾股定理得AD=x,分别求出圆的面积与正方形的面积,利用圆的面积除以正方形的面积,即得结论.
12.;
13.C
解:A、∵令2p 1=17,∴2p=18,p不是正整数,∴A不符合题意;
B、∵令2p 1=15,∴2p=16=24,可得p=4,4是合数,∴B不符合题意;
C、∵令2p 1=7,∴2p=8=23,可得p=3,∴C符合题意;
D、∵令2p 1=1,∴2p=2,可得p=1,1不是质数,∴D不符合题意.
故答案为:C.
利用“ 梅森素数 ”的定义逐项分析判断即可.
14.B
解:记an=
S=a 1+a2 +……+ a1003,用{x}表示x的小数部分,则x=[x] +{x},
∵,
n=1,2,……, 1003,
又∵ 是整数,
∴也是整数,
又∵0<<1,0<<1,
则=1,
∴,
∵2007=3×669,2001=3×667,
∴当n=669时,2007|2001×669,2007|2001×(2007-669),此时不适用以上配对结果,
∴,
∴S=2000×1002+2001= 2006001.
故答案为:B.
首尾两数相加,分别将加数分为1003组,每组和记为an=,又,故可得两数的小数部分和为1,进而求得,当n=669时,为整数,不是整数,此时不适用以上配对结果,求得,最终可得S= 2006001.
15.D
16.B
解:设分别为
∵,
∴,
∴,
∴,
∴该三角形的形状是直角三角形,
故答案为:B
先根据比例设分别为进而根据三角形内角和定理求出k,从而根据直角三角形的判定即可求解。
17.C
18.C
解:如下图,延长,交于点,,
∵边长为2的正方形的中心与半径为2的的圆心重合,
∴图中阴影部分的面积.
故答案为:C.
延长,交于点,,根据边长为2的正方形的中心与半径为2的的圆心重合可得:,再利用圆和正方形的面积公式进行计算可求出答案.
19.(1)133
(2)
(3)
(4)
20.(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
(9)
(10)
21.解:①原式=
=
=;
②,
解得:x=1;
③原式=8.6×(8.6+0.4+1)
=8.6×10
=86;
④原式=
(1)按照有理数的混合运算法则,先算乘法,再去括号,再进行加减运算即可;
(2)先合并同类项,再系数化为1即可;
(3)利用乘法对加法的分配律,先提取8.6,剩余部分相加再与8.6相乘即可;
(4)观察发现每个分数的分母都可以拆分成相邻两个整数的乘积,利用对各项进行拆分,再进行加减运算即可.
22.(1)
(2)
23.(1)
(2)
(3)
24.
25.解:小圆的周长,
大半圆的周长,
∴阴影部分的周长,
小圆的面积,
大半圆的面积,
∴阴影部分的面积.
本题考查了圆的周长公式和面积公式,掌握圆的周长公式,面积公式,并能根据图形找出阴影的周长组成部分是解题的关键.
26.(1)解:
(元)
答:这个月伙食支出最多,支出了1260元
(2)解:
,
答:购买衣服比文化教育支出少
(1)要求这个月哪项支出最多 比较各项支出的百分数即可,百分号前面的数越大,这个百分数就越大要求一共支出了多少钱,用文化教育支出的钱数÷文化教育支出占总支出的百分比=总支出,然后用总支出×伙食支出占总支出的百分比=伙食支出,据此列式;
(2)把文化教育支出看作单位“1”,先求出购买衣服支出比文化教育支出少占总支出的百分之几,然后根据求一个数是另一个数的百分之几用除法,即可计算出其结果.
(1)解:
(元)
答:这个月伙食支出最多,支出了1260元;
(2)解:
,
答:购买衣服比文化教育支出少.
27.这本故事书共有200页.
28.(1)
(2)①1;②③或
29.(1)圆柱;1
(2)解:该几何体的侧面积为:;
该几何体的体积.
解:(1)该几何体的名称是圆柱,其底面半径为1.
故答案为:圆柱;1;
(1)根据几何体的展开图可得该几何体为圆柱,根据圆的直径可得底面圆的半径;
(2)根据圆柱侧面展开矩形的长为底面圆的周长结合圆的周长公式可得矩形的长,根据矩形的面积公式可得侧面积,根据圆柱的体积V=πr2h可得体积.
20224-2025学年六年级上册期末模拟卷(沪教版)
数学
考试范围:六上全册 考试时间:100分钟 分值:100分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
一、填空题(共24分)
1.分解素因数:18= 。
2. 数的倒数是 .
3.在,,,中最大的数是 .
4.求比值: .
5.如果,那a与b成 比例,比值是 .
6.饮料厂从一批产品中抽查了40瓶饮料,其中8瓶不合格,合格率是 .
7.是 的, 比多.
8.在物理课上,某实验的电路图如图所示,其中S1,S2,S3表示电路的开关,L表示小灯泡,R为保护电阻.若闭合开关S1,S2,S3中的任意两个,则小灯泡L发光的概率为 .
9.如图,在矩形ABCD中,AB=4,AD=6,P是边BC上一动点(不与点B、C重合).连接AP,过点D作DE⊥PA,垂足为E,则线段BE长的最小值为 .
10.一批零件,原计划按分配给师徒两人加工,结果师傅加工1200个,超过分配任务的,而徒弟因病只完成了他原定任务的,徒弟实际加工了 个.
11.如图,一枚圆形古钱币的中间是一个正方形孔,已知圆的直径与正方形的对角线之比为3∶1,则圆的面积约为正方形面积的 倍.(精确到个位)
12.有大小两个圆,大圆直径是小圆直径的2.5倍,大圆的周长与小圆的周长比是 ,面积比是 .
二、选择题(共12分)
13.古希腊数学家欧几里得证明了素数也就是质数有无限多个,提出少量素数可以写成“”的形式,这里的也是一个素数千百年来一直吸引着众多的数学家对它进行研究和探索,世纪法国著名数学家马林梅森是其中成果较为卓著的一位,因此后人将“”型的素数称为梅森素数下面个数中,( )是梅森素数注:表示个相乘
A. B. C. D.
14.(第十九届“五羊杯”初中数学竞赛七年级)S==( ).(其中[x]表示不超过x的最大整数)
A.2006000 B.2006001 C.2007003 D.4014006
15.下列式子中,正确运用分数基本性质的是( )
A. B. C. D.
16.的三角之比是,则是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.无法确定
17.若圆的直径和正方形的边长都是,则圆的周长( )正方形的周长.
A.大于 B.等于 C.小于 D.不能确定
18.如图,边长为2的正方形的中心与半径为2的的圆心重合,,分别是,的延长线与的交点,则图中阴影部分的面积为( )
A. B. C. D.
三、简答题(共30分)
19.用简便方法计算.
(1)
(4)
20.直接写得数
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
(9)
(10)
21.计算题:
①;
②求未知数:;
③;
④.
22.求未知数x.
(1);
(2).
23.化简比.
(1)
(2)小时分:小时分
(3)升:升毫升
学校原有足球、篮球一共个,足球与篮球个数之比是,后来又买回一些足球,这时足球与两种球总个数之比是,求又买回多少个足球.
四、解答题(共26分)
25.求阴影部分的周长及面积.(结果保留)
26.小明家2020年12月份的总支出是3600元,看图回答问题.
(1)这个月哪项支出最多?支出了多少元?
(2)购买衣服比文化教育支出少百分之几?
一本故事书,李红第一天看了全书的,第二天看了30页,这时已看页数与未看页数的比是,这本故中书有多少页?
28.如图1,在正方形中,,点 O,E在边上,且,,以点O为圆心,为半径在其左侧作半圆O,出分别交于点 G,交的延长线于点F.
(1) ______;
(2)将半圆O绕点E逆时针旋转 ,点O 的对应点为,点 F 的对应点为.
①如图2,若M为半圆上一点,当点落在边上时,求点M到线段的最短距离;
②如图3,当半圆交于P,R两点时,若 ,求此时半圆与正方形重叠部分的面积;
③当半圆与正方形的边相切时,设切点为N,直接写出的值.
五、综合题(共8分)
29.如图所示是一个几何体的表面展开图.
(1)该几何体的名称是 ,其底面半径为 .
(2)根据图中所给信息,求该几何体的侧面积和体积(结果保留)
答案解析部分
1.2×3×3
解:18=2×3×3。
故答案为:2×3×3。
分解素因数,要从最小的素数除起,一直除到结果为素数为止。
2.-3
解:由题意可得:
的倒数是-3
故答案为:-3
根据代数的定义即可求出答案.
3.
解:∵,
∴
∴所以最大的数是
故答案为:.
先把,,然后得出:∴,而,因此可得:
.
4.
5.正;
6.80%
解:(40-8)÷40=0.8=80%.
故答案为:80%.
先求出合格的瓶数,用合格瓶数除以40即可.
7.;
根据题意可得:6÷=10;2×(1+50%)=3,
故答案为:10;3.
根据分数乘除法列出算式求解即可.
8.
解:列表如下:
S1 S2 S3
S1 —— (S1,S2) (S1,S3)
S2 (S2,S1) —— (S2,S3)
S3 (S3,S1) (S3,S2) ——
共有6中可能的情况,当闭合S1、S3 时灯泡才亮,
∴则小灯泡L发光的概率为.
故答案为:.
用列表法列出所有的情况,当闭合S1、S3 时灯泡才亮,所以情况有2种,从而根据概率公式即可得出小灯泡L发光的概率为.
9.2.
10.360
解:师傅的任务(个)
徒弟的任务(个)
徒弟实际加工(个)
答:徒弟实际加工了360个.
故答案为:360.
先用师傅实际加工零件的个数除以其占比求出师傅的任务,进而可求出徒弟的任务,再用徒弟的任务乘以60%,可求出徒弟实际加工的个数.
11.14
解:如图
由题意得AC与EF共线
∵圆的直径与正方形的对角线之比为3:1
∴EF:AC=3:1
∴OE:OA=3:1
设OE=3x,OA= x
在正方形ABCD中
由勾股定理得:AD=x
∴圆的面积为:π×(3x)2=9πx2
正方形的面积为(x)2=2 x2
∴9πx2÷2 x2=≈14
故答案为:14
如图,由圆的直径与正方形的对角线之比为3:1,可得EF:AC=3:1,即得OE:OA=3:1;设OE=3x,OA= x,由勾股定理得AD=x,分别求出圆的面积与正方形的面积,利用圆的面积除以正方形的面积,即得结论.
12.;
13.C
解:A、∵令2p 1=17,∴2p=18,p不是正整数,∴A不符合题意;
B、∵令2p 1=15,∴2p=16=24,可得p=4,4是合数,∴B不符合题意;
C、∵令2p 1=7,∴2p=8=23,可得p=3,∴C符合题意;
D、∵令2p 1=1,∴2p=2,可得p=1,1不是质数,∴D不符合题意.
故答案为:C.
利用“ 梅森素数 ”的定义逐项分析判断即可.
14.B
解:记an=
S=a 1+a2 +……+ a1003,用{x}表示x的小数部分,则x=[x] +{x},
∵,
n=1,2,……, 1003,
又∵ 是整数,
∴也是整数,
又∵0<<1,0<<1,
则=1,
∴,
∵2007=3×669,2001=3×667,
∴当n=669时,2007|2001×669,2007|2001×(2007-669),此时不适用以上配对结果,
∴,
∴S=2000×1002+2001= 2006001.
故答案为:B.
首尾两数相加,分别将加数分为1003组,每组和记为an=,又,故可得两数的小数部分和为1,进而求得,当n=669时,为整数,不是整数,此时不适用以上配对结果,求得,最终可得S= 2006001.
15.D
16.B
解:设分别为
∵,
∴,
∴,
∴,
∴该三角形的形状是直角三角形,
故答案为:B
先根据比例设分别为进而根据三角形内角和定理求出k,从而根据直角三角形的判定即可求解。
17.C
18.C
解:如下图,延长,交于点,,
∵边长为2的正方形的中心与半径为2的的圆心重合,
∴图中阴影部分的面积.
故答案为:C.
延长,交于点,,根据边长为2的正方形的中心与半径为2的的圆心重合可得:,再利用圆和正方形的面积公式进行计算可求出答案.
19.(1)133
(2)
(3)
(4)
20.(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
(9)
(10)
21.解:①原式=
=
=;
②,
解得:x=1;
③原式=8.6×(8.6+0.4+1)
=8.6×10
=86;
④原式=
(1)按照有理数的混合运算法则,先算乘法,再去括号,再进行加减运算即可;
(2)先合并同类项,再系数化为1即可;
(3)利用乘法对加法的分配律,先提取8.6,剩余部分相加再与8.6相乘即可;
(4)观察发现每个分数的分母都可以拆分成相邻两个整数的乘积,利用对各项进行拆分,再进行加减运算即可.
22.(1)
(2)
23.(1)
(2)
(3)
24.
25.解:小圆的周长,
大半圆的周长,
∴阴影部分的周长,
小圆的面积,
大半圆的面积,
∴阴影部分的面积.
本题考查了圆的周长公式和面积公式,掌握圆的周长公式,面积公式,并能根据图形找出阴影的周长组成部分是解题的关键.
26.(1)解:
(元)
答:这个月伙食支出最多,支出了1260元
(2)解:
,
答:购买衣服比文化教育支出少
(1)要求这个月哪项支出最多 比较各项支出的百分数即可,百分号前面的数越大,这个百分数就越大要求一共支出了多少钱,用文化教育支出的钱数÷文化教育支出占总支出的百分比=总支出,然后用总支出×伙食支出占总支出的百分比=伙食支出,据此列式;
(2)把文化教育支出看作单位“1”,先求出购买衣服支出比文化教育支出少占总支出的百分之几,然后根据求一个数是另一个数的百分之几用除法,即可计算出其结果.
(1)解:
(元)
答:这个月伙食支出最多,支出了1260元;
(2)解:
,
答:购买衣服比文化教育支出少.
27.这本故事书共有200页.
28.(1)
(2)①1;②③或
29.(1)圆柱;1
(2)解:该几何体的侧面积为:;
该几何体的体积.
解:(1)该几何体的名称是圆柱,其底面半径为1.
故答案为:圆柱;1;
(1)根据几何体的展开图可得该几何体为圆柱,根据圆的直径可得底面圆的半径;
(2)根据圆柱侧面展开矩形的长为底面圆的周长结合圆的周长公式可得矩形的长,根据矩形的面积公式可得侧面积,根据圆柱的体积V=πr2h可得体积.
同课章节目录
