2024-2025学年人教版版五年级数学上册期末押题卷(含答案)
文档属性
| 名称 | 2024-2025学年人教版版五年级数学上册期末押题卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 490.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-08 23:04:23 | ||
图片预览




文档简介
保密★启用前
20224-2025学年五年级上册期末押题卷(人教版)
数学
考试范围:五上全册 考试时间:100分钟 分值:100分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
一、认真读题,专心填写。(每空1分,共24分)
1. 在横线上填上“>”“<”或“=”。
2.在 2.15、、、2.1515 这四个数中,最大的是 ,最小的是 。
3. 循环小数化分数: = , =
4.按制作墨用的主要原料可以分为松烟墨、油烟墨、油松墨、五彩墨四种。下表是某店各种墨条的库存。
墨条种类 松烟墨 油烟墨 油松墨 五彩墨
库存量 39 17 31 5
(1)任意从库存中取出1个墨条,最有可能是 。
(2)从库房中取出5根墨条,前4次取出的都是松烟墨,则第5次取出的 五彩墨。(填“一定”“可能”“不可能”)
5.在下面的横线里填上“>”、“<”或“=”。
3.85×0.7 3.85÷0.7 2.62 2.6×2
4.36×0.5 0.436×5
6.一个三角形和一个平行四边形等底等面积,如果平行四边形的高是 10 cm,那么三角形的高是 cm;如果三角形的高是10 cm,那么平行四边形的高是 cm。
7.若3x+2y-8=0,则55-9x-6y的值是 。
8.农民伯伯在阴影部分的农田里种植西红柿,则种植西红柿的农田的面积是 m2。
9. 甲、乙两车同时从A城开往B城。3小时后,乙车超过甲车22.5千米,甲车平均每小时行75千米,乙车平均每小时行 千米。
10.奇奇妈妈用图钉将彩带按照一定的顺序钉在了毛毡板上制作成派对主题背景板。
(1)请你仔细观察彩带的条数与分出绳子的段数之间的关系并填写下表;
彩带/条 1 2 3 4 5 6 7 8
绳子段数/段
(2)若第1条彩带到最后一条彩带的距离是187.6厘米,则相邻两条彩带之间的间距是 厘米。
二、反复比较,巧思妙选。(每题1分,共8分)
11.王老师买了 akg苹果, 每千克18.8元, 又买了 bkg梨, 每千克14.6元,那么18.8a-14.6b 表示( ) 。
A.买苹果和梨一共花了多少钱?
B.苹果比梨重多少千克?
C.每千克苹果比每千克梨贵多少钱?
D.买梨比买苹果少花多少钱?
12.得数是6.3的算式是( )。
A.6.3÷100 B.0.63×10 C.0.63÷0.01
13.在两条平行线之间有3个不同的图形(如图),把它们按面积从小到大的顺序排列是( )。
A.①<②<③ B.②<①<③ C.①<③<② D.③<①<②
14.蒙古族服饰艺术节即将开幕,在蒙古族服装设计大赛中,举办方为设计师们准备了三个等级的奖券共40张。要使一等奖奖券最少,三等奖的奖券最多,则二等奖奖券最少应该设置( )张。
A.1 B.2 C.20 D.21
15.【新角度】在方格纸上,如果每个小方格的边长都表示1cm,那么在这个方格纸上画一个半径是 2 cm 的圆,圆心的位置不可能是( )。
A.(2,4) B.(4,2) C.(2,0) D.(3,4)
16.如果在每个□里填一个数字,下面直线上M点表示的数可能是算式( )的得数。
A.19×0.9□ B.4.□×4.□ C.19÷1.□ D.4.□×5.□
17.如图中的天平都处于平衡状态,则“○”与“□”的质量关系是( )。
A.2 =3□ B.4 =9□ C.○=2□ D.O=□
18.如图是梯形转化成三角形的过程,如果梯形的面积是54平方厘米,高是9厘米,那么转化后,三角形的底是( )厘米。
A.3 B.6 C.12
三、注意审题,合理计算。(共33分)
19.直接写出得数
4.5×0.2= 5x×x= 3.6÷(3.6÷0.4)=
2.56-1.6= 3.2a÷8= 1.6×0.7÷1.6×0.7=
20.列竖式计算,带★的要验算。
3.25×2.4 1.8×2.5
★4.48÷3.2 0.568÷3.4(得数保留两位小数)
21. 解方程。
(1)
(2)
22. 计算下面各题,怎样简便就怎样算。
9.2÷0.125÷8 25.25×0.4
2.021×390+20.21×41+202.1×2
四、动手操作,图形计算。(共11分)
23.一辆汽车在高速公路上行驶的路程和耗油量的关系如下表:
路程(km) 0 50 100 150 200 250 …
耗油量(L) 0 5 10 15 20 25 …
(1)根据表中的数据,在图中描出这辆汽车行驶的路程和耗油量所对应的点,再把它们按顺序连起来。
(2)【说理题】这辆汽车在高速公路上行驶的路程和耗油量成什么比例?为什么?
(3)根据图象推算,这辆汽车行驶350km的耗油量。
(4)这辆汽车出发时油箱里有汽油40 L,如果汽车要在高速公路上行驶460km,那么你认为司机在途中需要加油吗?
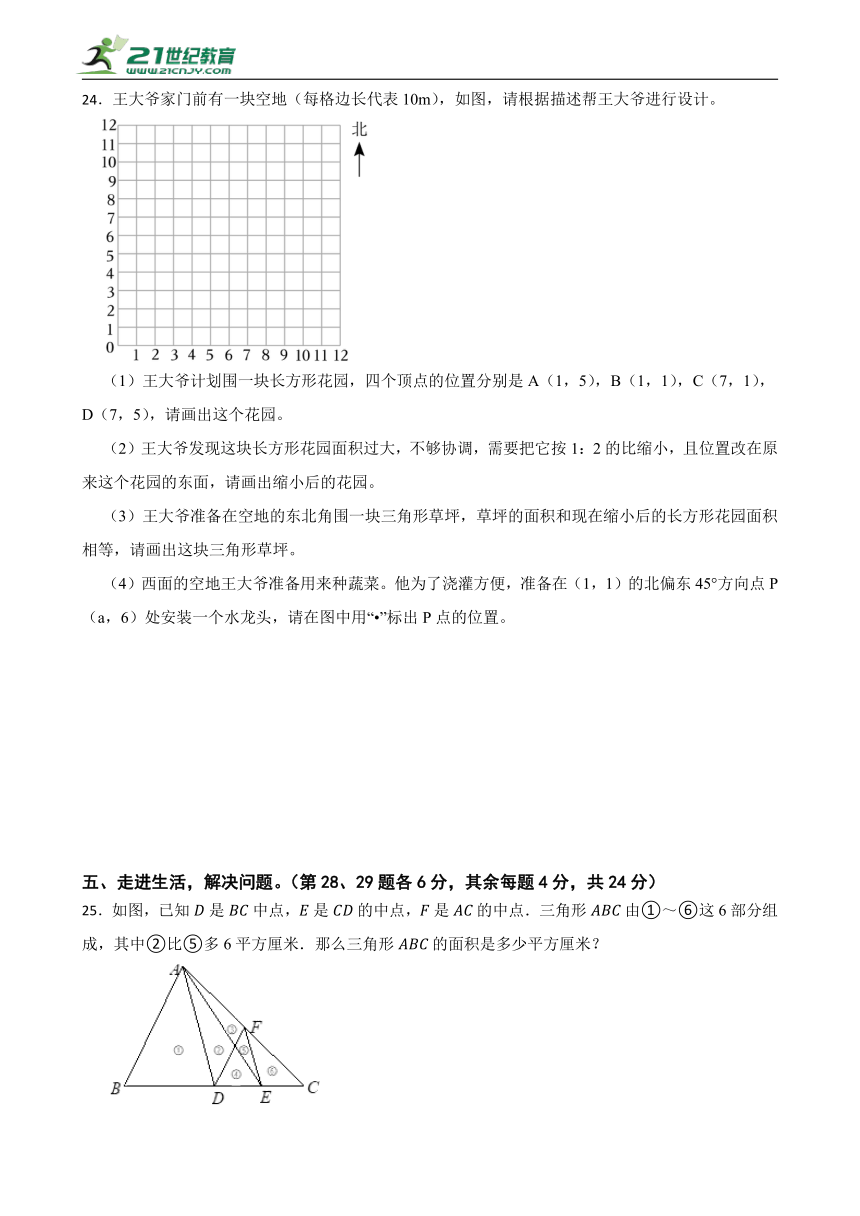
24.王大爷家门前有一块空地(每格边长代表10m),如图,请根据描述帮王大爷进行设计。
(1)王大爷计划围一块长方形花园,四个顶点的位置分别是A(1,5),B(1,1),C(7,1),D(7,5),请画出这个花园。
(2)王大爷发现这块长方形花园面积过大,不够协调,需要把它按1:2的比缩小,且位置改在原来这个花园的东面,请画出缩小后的花园。
(3)王大爷准备在空地的东北角围一块三角形草坪,草坪的面积和现在缩小后的长方形花园面积相等,请画出这块三角形草坪。
(4)西面的空地王大爷准备用来种蔬菜。他为了浇灌方便,准备在(1,1)的北偏东45°方向点P(a,6)处安装一个水龙头,请在图中用“ ”标出P点的位置。
五、走进生活,解决问题。(第28、29题各6分,其余每题4分,共24分)
25.如图,已知是中点,是的中点,是的中点.三角形由①~⑥这6部分组成,其中②比⑤多6平方厘米.那么三角形的面积是多少平方厘米?
26.王老师有一张电影票,电影票的排数与座位号的乘积是216,而且座位号比排数大6。王老师的电影票是几排几号?
27.为进一步提升学生体育素养,增强学生体质,学校新采购了一批体育用品。下面是相关信息。
①每副羽毛球拍24.8元。
②每副乒乓球拍16.5元。
③这次买这两种用品共花费545.1元。
④其中买乒乓球拍用了247.5元。
(1)根据上面的信息,淘气列算式“(545.1-247.5)÷24.8”要解决的是什么问题?写出问题并解答。
问题:________________________
解答:
(2)根据给出的信息,再提出一个数学问题并解答。
28.一批中性笔原价5.5元/支,班主任老师准备购买120支。现降价销售每支便宜1.5元。
(1)算式5.5×120解决的问题是 。
(2)算式5.5×120÷(5.5-1.5)解决的问题是 。
29.(附加题)甲、乙两辆车同时从A, B两地相对开出,几小时后在距中点40千米处相遇。已知甲车行完全程要8小时,乙车行完全程要10小时,A,B两地相距多少千米?
答案解析部分
1.>;<;>;=
解:因为0.99<1,所以5.78÷0.99>5.78;
因为0.98<1,所以12×0.98<12,12÷0.98>12,12×0.98<12÷0.98;
因为=0.5656……,=0.0566……,0.5656……>0.0566……,所以>;
36÷0.01=36×100。
故答案为:>;<;>;=。
在除法里,一个非0数除以小于1的非0数,商大于被除数,一个非0数除以大于1的数,商小于被除数;
在乘法里,一个非0数乘小于1的非0数,积小于这个数,一个非0数乘大于1的数,积大于这个数,据此比较大小;
比较两个循环小数的大小,先把循环小数写成一般形式,再比较大小。
2.;2.15
解:=2.155……
=2.1515……
2.155……>2.1515……>2.1515>2.15
故答案为:;2.15 。
比较小数的大小:先看它们的整数部分,整数部分大的那个数就大;整数部分相同的,十分位上的数大的那个数就大;十分位上的数也相同的,百分位上的数大的那个数就大……。
3.;
解:由于是纯循环小数,我们直接应用公式:,
由于是混循环小数,我们应用公式:;
故答案为:;。
循环小数化为分数需要使用特定的公式。对于纯循环小数(即从第一位开始循环),公式为:,对于混循环小数(即从第二位或之后开始循环),公式为:,其中,abc是循环节的数字,a是循环节前的数字(对于纯循环小数,a为0)。
4.(1)松烟墨
(2)可能
解:(1)松烟墨;
(2)可能.
故答案为:松烟墨;可能
(1)库存中松烟墨的数量最多,故任意从库存中取出1个墨条,最有可能是松烟墨;
(2) 前4次取出的都是松烟墨 ,在第五次取的时候库房里各种墨条都有,故取出那个都有可能,所以第五次取出的可能是五彩墨.
5.<;>;=;<
解:0.7<1,所以3.85×0.7<3.85÷0.7;2.62>2.6×2;
4.36×0.5=0.436×5,<。
故答案为:<;>;=;<。
一个非0数乘比0大比1小的数,所得的结果比这个数小;
一个非0数除以比0大比1小的数,所得的结果比这个数大;
一个数乘的数越大,积就越大;
比较小数的大小,先比较整数部分,整数部分大的这个数就大,整数部分相同,就比较十分位上的数,然后依次进行比较即可。
6.20;5
因为一个三角形和一个平行四边形等底等面积,
又因为三角形的面积为,平行四边形的面积为,
所以,平行四边形的高是三角形高的一半,
又因为平行四边形的高是10 cm,那么三角形的高是20cm;
如果三角形的高是10 cm,那么平行四边形的高是cm.
故填:20;5.
利用一个三角形和一个平行四边形等底等面积,再结合三角形的面积和平行四边形的面积公式,从而得出平行四边形的高是三角形高的一半,进而得出答案.
7.31
解:根据题意,可得
3x+2y-8=0
所以,3x+2y=8
则 55-9x-6y
=55-3(3x+2y)
=55-3×8
=55-24
=31
故答案为:31
先将3x+2y-8=0进行化简:3x+2y=8,然后再对式子55-9x-6y进行变形:55-3(3x+2y),然后再将3x+2y=8代入即可求解
8.60
解:12×8-12×6÷2
=96-72÷2
=96-36
=60(m2)
故答案为:60。
观察图形,得出阴影部分的面积=平行四边形的面积-三角形面积,故只需根据“平行四边形的面积=底×高”和“三角形的面积=底×高÷2”计算即可。
9.82.5
解:(75×3+22.5)÷3
=247.5÷3
=82.5(千米)。
故答案为:82.5。
乙车的速度=(甲车的速度×行驶的时间+乙车超过甲车的路程)÷行驶的时间。
10.(1)
彩带/条 1 2 3 4 5 6 7 8
绳子段数/段 2 3 4 5 6 7 8 9
(2)26.8
解:(1)1+1=2;2+1=3;3+1=4;4+1=5;6+1=7;7+1=8;8+1=9;
(2)因为从第1条彩带到最后一条,间隔数为8-1=7(个),间隔=187.6÷7=26.8(厘米)。
故答案为:(1)2;3;4;5;6;7;8;9;(2)26.8。
(1)根据题图可知,绳子段数=彩带条数+1;
(2)间距=总长÷间隔数,间隔数=彩带数-1,据此解答。
11.D
解:18.8b表示梨的总价,14.6b表示苹果的总价,18.8a-14.6b表示买梨比苹果少花多少钱。
故答案为:D。
根据“单价×数量=总价”分别判断出18.8a和14.6b表示的意义,然后判断这个式子表示的意义即可。
12.B
解:A项中,6.3÷100=0.063;
B项中,0.63×10=6.3。
C项中,0.63÷0.01=63。
故答案为:B。
一个小数除以100,就是把小数点向左移动两位;
一个小数乘10,就是把小数点向右移动一位;
一个小数除以0.01,就是把小数点向右移动两位。
13.C
解:三个图形的高相等,设为h,
①的面积:8×h÷2=4h;
②的面积:5×h=5h;
③的面积:(3+6)×h÷2=4.5h;
4h<4.5h<5h,①<③<②。
故答案为:C。
两条平行线之间的距离处处相等,三个图形的高相等,可以设为h,分别表示出三个图形的面积,最后按从小到大的顺序排列。
14.B
解:每种奖券都有,且一等奖的奖券数量最少,则假设只设置了1 张一等奖奖券,此时剩余有39张,又因为二等奖奖券数量既不是最多也不是最少,且三等奖奖券数量最多,所以二等奖奖券最少应该设置2张,此时三等奖奖券数量最多, 有37张。
故答案为:B。
根据题意可知,一等奖的奖券数量应该最小,假设只有1张一等奖奖券,40张奖券还剩39张,剩下的为二等奖和三等奖,二等奖最少可以设置2张,剩下的是三等奖,据此解答。
15.C
解:选项A:数对(2,4)表示第2列第4行,距离方格纸左边边缘2厘米,下边边缘4厘米,都大于等于圆的半径,所以可以以(2,4)为圆心画一个半径是2cm的圆;
选项B:数对(4,2)表示第4列第2行,距离方格纸左边边缘4厘米,下边边缘2厘米,都大于等于圆的半径,所以可以以(4,2)为圆心画一个半径是2cm的圆;
选项C:数对(2,0)表示第2列第0行,距离方格纸左边边缘2厘米,下边边缘0厘米,下边边缘的距离小于2厘米,所以无法以(2,0)为圆心画一个半径是2cm的圆;
选项D:数对(3,4)表示第3列第4行,距离方格纸左边边缘3厘米,下边边缘4厘米,都大于等于圆的半径,所以可以以(3,4)为圆心画一个半径是2cm的圆;
故答案为:C。
在方格纸上画的圆,圆心距离方格纸的边要大于等于半径的长度,据此解答。
16.B
解:直线上M点表示的数可能是算式4.□×4.□的得数。
故答案为:B。
A项中,19×0.9□的结果会更靠近20,而M点在19和20的中间靠近19的位置,所以不合适;
B项中,4.3×4.5=19.35,所以合适;
C项中,19÷1.□<19,所以不合适;
D项中,4×5=20,所以4.□×5.□不合适。
17.B
解:根据题意,可得
2个○=3个△,解得,1个△=
2个△=3个□,解得,1个□=
将1个△=代入1个□=,可得
1个□=
=
所以,9个□=4个○
故答案为:B
根据左边天平,可知,天平的左边有2个○,右边3个△,建立方程:2个○=3个△,求出1个△=;再根据右边天平,可知,天平的左边有2个△,右边有3个□,建立方程:2个△=3个□,求出1个□=,然后再将1个△=代入1个□=,求出□和○的关系,
18.C
解:梯形转化成三角形后,三角形的底是梯形的上下底之和,
54×2÷9=12(厘米)
三角形的底是12厘米。
梯形的面积×2÷梯形的高=梯形的上下底之和。
19.
4.5×0.2=0.9 5x×x=5x2 3.6÷(3.6÷0.4)=0.4
2.56-1.6=0.96 3.2a÷8=0.4a 1.6×0.7÷1.6×0.7=0.49
根据题意,先算乘除、后算加减,有括号的先算括号里面的,据此解答。
20.解:3.25×2.4=7.8
1.8×2.5=4.5
★4.48÷3.2=1.4
验算:
0.568÷3.4≈0.17
计算小数乘法时,先按照整数乘法的计算方法计算出积,然后看两个因数中共有几位小数,就从积的右边向左数出几位点上小数点;除数是小数,先移动除数的小数点,使除数转化成整数,除数的小数点向右移动几位,被除数的小数点也向右移动几位,然后根据除数是整数的除法计算方法计算。
21.(1)解:0.75x-0.5x=25
0.25x=25
x=100
(2)解:
0.2x-0.2×3=1.6
0.2×(x-3)= 1.6
x-3=8
x=11
等式的基本性质1:等式两边同时加上(或减去)同一个整式,等式仍然成立;等式的基本性质2:等式两边同时乘或除以同一个不为0的整式,等式仍然成立;
(1)先将百分数和分数转化为小数,将含有x的式子合并,再等式两边同时除以0.25即可;
(2)将分数和百分数转化为小数,利用乘法结合律将式子化简,再左右两边同时除以0.2,最后等式两边同时加3即可。
22.解:9.2÷0.125÷8
=9.2÷(0.125×8)
=9.2÷1
=9.2
25.25×0.4
=(25+0.25)×0.4
=25×0.4+0.25×0.4
=10+0.1
=10.1
2.021×390+20.21×41+202.1×2
=20.21×39+20.21×41+20.21×20
=20.21×(39+41+20)
=2021
(1)先计算0.125×8,再计算9.2÷1,即可简算出答案,
(2)利用乘法分配律将 25.25拆分成(25+0.25)即可简便计算,
(2)利用小数乘法分配律提取公因数20.21即可简便运算
23.(1)解:
(2)解:=====.......=10,
行驶的路程和耗油量成正比例。因为行驶的路程和耗油量是两种相关联的量,耗油量随行驶路程的变化而变化,且=消耗每升汽油行驶的路程(一定),所以两者成正比例。
(3)解:根据图象推算,这辆汽车行驶350km的耗油量为35L。
(4)解:由(2)可得,消耗每升汽油行驶的路程为10km,
40×10=400(km),
400<460,
所以司机在途中需要加油。
(1)先描点,再连线;
(2)正比例的判断方法:相关联,能变化,商一定;
(3)把射线延长,横轴350千米对应横轴的数是35升,据此解答;
(4)消耗每升汽油行驶的路程×汽油的升数=可以行驶的路程,可以行驶的路程<460千米,在途中需要加油。
24.(1)解:
(2)解:
(3)解:
(4)解:
(1)数对中第一个数表示列,第二个数表示行,根据各点所在的列与行用数对表示,并画出这个长方形;
(2)按1:2缩小后的长方形长是3格,宽是2格,由此画出缩小后的长方形;
(3)缩小后长方形面积是6格,可以画一个底是5格,高是2格的三角形,面积和这个长方形面积相等;
(4)(a,6)在第6行。(1,1)点的北偏东45°方向与第6行的交叉点就是P点的位置。
25.解:因为 是 中点, 为 中点,有 且平行于 ,
则四边形 为梯形.
在梯形 中有③=④,②×⑤=③×④,②:⑤= : =4.
又已知②-⑤=6,
所以⑤= ,②=⑤ ,
所以②×⑤=④×④=16,
而③=④,
所以③=④=4,梯形 的面积为②、③、④、⑤四块图形的面积和,为 .
有 与 的面积比为 平方与 平方的比,即为1:4.
所以 面积为梯形 面积的 = ,即为 .
因为 是 中点,
所以 与 的面积相等,而 的面积为 、 的面积和,即为 平方厘米.
答:三角形 的面积为48平方厘米。
本题主要运用几何的代换将三角形ABC的面积转化为三角形ABD与三角形ADC面积的和,运用了蝴蝶模型的三大性质和等积变形。
26.解:设排数为x,座位号为x+6,
x×(x+6)=216
x=12
或x=﹣18(不合题意,舍去)
12+6=18(号)
答:王老师的电影票是12排18号。
根据题意,可设排数为x,则座位号为x+6,根据题意可得到等量关系式:排数×座位号的乘积是216,把未知数代入等量关系式进行计算即可得到答案。
27.解:(1)(545.1-247.5)÷24.8,要解决的问题是:学校新采购了多少副羽毛球拍?
(2)学校新采购了多少副乒乓球拍?
247.5÷16.5=15(副)
答:学校新采购了15副乒乓球拍。
(1)学校新采购羽毛球拍的副数=(这次买这两种用品共花费的钱数-其中买乒乓球拍用的钱数)÷每副羽毛球拍的单价;
(2)学校新采购乒乓球拍的副数=买乒乓球拍用的钱数÷每副乒乓球拍的单价。
28.(1)原来买120支的总价
(2)原来买120支的钱数现在可以买的支数
解:(1)算式5.5×120解决的问题是:原来买120支的总价;
(2)算式5.5×120÷(5.5-1.5)解决的问题是:原来买120支的钱数现在可以买的支数。
故答案为:(1)原来买120支的总价;(2)原来买120支的钱数现在可以买的支数。
(1)原来买120支的总价=原来的单价×数量;
(2)原来买120支的钱数现在可以买的支数=运来中性笔的单价×原来买的支数÷(运来中性笔的单价-现在每支便宜的钱数)。
29.解:40×2÷(10-8)×(10+8)
=80÷2×18
=40×18
=720(千米)
答:A,B两地相距720千米
20224-2025学年五年级上册期末押题卷(人教版)
数学
考试范围:五上全册 考试时间:100分钟 分值:100分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
一、认真读题,专心填写。(每空1分,共24分)
1. 在横线上填上“>”“<”或“=”。
2.在 2.15、、、2.1515 这四个数中,最大的是 ,最小的是 。
3. 循环小数化分数: = , =
4.按制作墨用的主要原料可以分为松烟墨、油烟墨、油松墨、五彩墨四种。下表是某店各种墨条的库存。
墨条种类 松烟墨 油烟墨 油松墨 五彩墨
库存量 39 17 31 5
(1)任意从库存中取出1个墨条,最有可能是 。
(2)从库房中取出5根墨条,前4次取出的都是松烟墨,则第5次取出的 五彩墨。(填“一定”“可能”“不可能”)
5.在下面的横线里填上“>”、“<”或“=”。
3.85×0.7 3.85÷0.7 2.62 2.6×2
4.36×0.5 0.436×5
6.一个三角形和一个平行四边形等底等面积,如果平行四边形的高是 10 cm,那么三角形的高是 cm;如果三角形的高是10 cm,那么平行四边形的高是 cm。
7.若3x+2y-8=0,则55-9x-6y的值是 。
8.农民伯伯在阴影部分的农田里种植西红柿,则种植西红柿的农田的面积是 m2。
9. 甲、乙两车同时从A城开往B城。3小时后,乙车超过甲车22.5千米,甲车平均每小时行75千米,乙车平均每小时行 千米。
10.奇奇妈妈用图钉将彩带按照一定的顺序钉在了毛毡板上制作成派对主题背景板。
(1)请你仔细观察彩带的条数与分出绳子的段数之间的关系并填写下表;
彩带/条 1 2 3 4 5 6 7 8
绳子段数/段
(2)若第1条彩带到最后一条彩带的距离是187.6厘米,则相邻两条彩带之间的间距是 厘米。
二、反复比较,巧思妙选。(每题1分,共8分)
11.王老师买了 akg苹果, 每千克18.8元, 又买了 bkg梨, 每千克14.6元,那么18.8a-14.6b 表示( ) 。
A.买苹果和梨一共花了多少钱?
B.苹果比梨重多少千克?
C.每千克苹果比每千克梨贵多少钱?
D.买梨比买苹果少花多少钱?
12.得数是6.3的算式是( )。
A.6.3÷100 B.0.63×10 C.0.63÷0.01
13.在两条平行线之间有3个不同的图形(如图),把它们按面积从小到大的顺序排列是( )。
A.①<②<③ B.②<①<③ C.①<③<② D.③<①<②
14.蒙古族服饰艺术节即将开幕,在蒙古族服装设计大赛中,举办方为设计师们准备了三个等级的奖券共40张。要使一等奖奖券最少,三等奖的奖券最多,则二等奖奖券最少应该设置( )张。
A.1 B.2 C.20 D.21
15.【新角度】在方格纸上,如果每个小方格的边长都表示1cm,那么在这个方格纸上画一个半径是 2 cm 的圆,圆心的位置不可能是( )。
A.(2,4) B.(4,2) C.(2,0) D.(3,4)
16.如果在每个□里填一个数字,下面直线上M点表示的数可能是算式( )的得数。
A.19×0.9□ B.4.□×4.□ C.19÷1.□ D.4.□×5.□
17.如图中的天平都处于平衡状态,则“○”与“□”的质量关系是( )。
A.2 =3□ B.4 =9□ C.○=2□ D.O=□
18.如图是梯形转化成三角形的过程,如果梯形的面积是54平方厘米,高是9厘米,那么转化后,三角形的底是( )厘米。
A.3 B.6 C.12
三、注意审题,合理计算。(共33分)
19.直接写出得数
4.5×0.2= 5x×x= 3.6÷(3.6÷0.4)=
2.56-1.6= 3.2a÷8= 1.6×0.7÷1.6×0.7=
20.列竖式计算,带★的要验算。
3.25×2.4 1.8×2.5
★4.48÷3.2 0.568÷3.4(得数保留两位小数)
21. 解方程。
(1)
(2)
22. 计算下面各题,怎样简便就怎样算。
9.2÷0.125÷8 25.25×0.4
2.021×390+20.21×41+202.1×2
四、动手操作,图形计算。(共11分)
23.一辆汽车在高速公路上行驶的路程和耗油量的关系如下表:
路程(km) 0 50 100 150 200 250 …
耗油量(L) 0 5 10 15 20 25 …
(1)根据表中的数据,在图中描出这辆汽车行驶的路程和耗油量所对应的点,再把它们按顺序连起来。
(2)【说理题】这辆汽车在高速公路上行驶的路程和耗油量成什么比例?为什么?
(3)根据图象推算,这辆汽车行驶350km的耗油量。
(4)这辆汽车出发时油箱里有汽油40 L,如果汽车要在高速公路上行驶460km,那么你认为司机在途中需要加油吗?
24.王大爷家门前有一块空地(每格边长代表10m),如图,请根据描述帮王大爷进行设计。
(1)王大爷计划围一块长方形花园,四个顶点的位置分别是A(1,5),B(1,1),C(7,1),D(7,5),请画出这个花园。
(2)王大爷发现这块长方形花园面积过大,不够协调,需要把它按1:2的比缩小,且位置改在原来这个花园的东面,请画出缩小后的花园。
(3)王大爷准备在空地的东北角围一块三角形草坪,草坪的面积和现在缩小后的长方形花园面积相等,请画出这块三角形草坪。
(4)西面的空地王大爷准备用来种蔬菜。他为了浇灌方便,准备在(1,1)的北偏东45°方向点P(a,6)处安装一个水龙头,请在图中用“ ”标出P点的位置。
五、走进生活,解决问题。(第28、29题各6分,其余每题4分,共24分)
25.如图,已知是中点,是的中点,是的中点.三角形由①~⑥这6部分组成,其中②比⑤多6平方厘米.那么三角形的面积是多少平方厘米?
26.王老师有一张电影票,电影票的排数与座位号的乘积是216,而且座位号比排数大6。王老师的电影票是几排几号?
27.为进一步提升学生体育素养,增强学生体质,学校新采购了一批体育用品。下面是相关信息。
①每副羽毛球拍24.8元。
②每副乒乓球拍16.5元。
③这次买这两种用品共花费545.1元。
④其中买乒乓球拍用了247.5元。
(1)根据上面的信息,淘气列算式“(545.1-247.5)÷24.8”要解决的是什么问题?写出问题并解答。
问题:________________________
解答:
(2)根据给出的信息,再提出一个数学问题并解答。
28.一批中性笔原价5.5元/支,班主任老师准备购买120支。现降价销售每支便宜1.5元。
(1)算式5.5×120解决的问题是 。
(2)算式5.5×120÷(5.5-1.5)解决的问题是 。
29.(附加题)甲、乙两辆车同时从A, B两地相对开出,几小时后在距中点40千米处相遇。已知甲车行完全程要8小时,乙车行完全程要10小时,A,B两地相距多少千米?
答案解析部分
1.>;<;>;=
解:因为0.99<1,所以5.78÷0.99>5.78;
因为0.98<1,所以12×0.98<12,12÷0.98>12,12×0.98<12÷0.98;
因为=0.5656……,=0.0566……,0.5656……>0.0566……,所以>;
36÷0.01=36×100。
故答案为:>;<;>;=。
在除法里,一个非0数除以小于1的非0数,商大于被除数,一个非0数除以大于1的数,商小于被除数;
在乘法里,一个非0数乘小于1的非0数,积小于这个数,一个非0数乘大于1的数,积大于这个数,据此比较大小;
比较两个循环小数的大小,先把循环小数写成一般形式,再比较大小。
2.;2.15
解:=2.155……
=2.1515……
2.155……>2.1515……>2.1515>2.15
故答案为:;2.15 。
比较小数的大小:先看它们的整数部分,整数部分大的那个数就大;整数部分相同的,十分位上的数大的那个数就大;十分位上的数也相同的,百分位上的数大的那个数就大……。
3.;
解:由于是纯循环小数,我们直接应用公式:,
由于是混循环小数,我们应用公式:;
故答案为:;。
循环小数化为分数需要使用特定的公式。对于纯循环小数(即从第一位开始循环),公式为:,对于混循环小数(即从第二位或之后开始循环),公式为:,其中,abc是循环节的数字,a是循环节前的数字(对于纯循环小数,a为0)。
4.(1)松烟墨
(2)可能
解:(1)松烟墨;
(2)可能.
故答案为:松烟墨;可能
(1)库存中松烟墨的数量最多,故任意从库存中取出1个墨条,最有可能是松烟墨;
(2) 前4次取出的都是松烟墨 ,在第五次取的时候库房里各种墨条都有,故取出那个都有可能,所以第五次取出的可能是五彩墨.
5.<;>;=;<
解:0.7<1,所以3.85×0.7<3.85÷0.7;2.62>2.6×2;
4.36×0.5=0.436×5,<。
故答案为:<;>;=;<。
一个非0数乘比0大比1小的数,所得的结果比这个数小;
一个非0数除以比0大比1小的数,所得的结果比这个数大;
一个数乘的数越大,积就越大;
比较小数的大小,先比较整数部分,整数部分大的这个数就大,整数部分相同,就比较十分位上的数,然后依次进行比较即可。
6.20;5
因为一个三角形和一个平行四边形等底等面积,
又因为三角形的面积为,平行四边形的面积为,
所以,平行四边形的高是三角形高的一半,
又因为平行四边形的高是10 cm,那么三角形的高是20cm;
如果三角形的高是10 cm,那么平行四边形的高是cm.
故填:20;5.
利用一个三角形和一个平行四边形等底等面积,再结合三角形的面积和平行四边形的面积公式,从而得出平行四边形的高是三角形高的一半,进而得出答案.
7.31
解:根据题意,可得
3x+2y-8=0
所以,3x+2y=8
则 55-9x-6y
=55-3(3x+2y)
=55-3×8
=55-24
=31
故答案为:31
先将3x+2y-8=0进行化简:3x+2y=8,然后再对式子55-9x-6y进行变形:55-3(3x+2y),然后再将3x+2y=8代入即可求解
8.60
解:12×8-12×6÷2
=96-72÷2
=96-36
=60(m2)
故答案为:60。
观察图形,得出阴影部分的面积=平行四边形的面积-三角形面积,故只需根据“平行四边形的面积=底×高”和“三角形的面积=底×高÷2”计算即可。
9.82.5
解:(75×3+22.5)÷3
=247.5÷3
=82.5(千米)。
故答案为:82.5。
乙车的速度=(甲车的速度×行驶的时间+乙车超过甲车的路程)÷行驶的时间。
10.(1)
彩带/条 1 2 3 4 5 6 7 8
绳子段数/段 2 3 4 5 6 7 8 9
(2)26.8
解:(1)1+1=2;2+1=3;3+1=4;4+1=5;6+1=7;7+1=8;8+1=9;
(2)因为从第1条彩带到最后一条,间隔数为8-1=7(个),间隔=187.6÷7=26.8(厘米)。
故答案为:(1)2;3;4;5;6;7;8;9;(2)26.8。
(1)根据题图可知,绳子段数=彩带条数+1;
(2)间距=总长÷间隔数,间隔数=彩带数-1,据此解答。
11.D
解:18.8b表示梨的总价,14.6b表示苹果的总价,18.8a-14.6b表示买梨比苹果少花多少钱。
故答案为:D。
根据“单价×数量=总价”分别判断出18.8a和14.6b表示的意义,然后判断这个式子表示的意义即可。
12.B
解:A项中,6.3÷100=0.063;
B项中,0.63×10=6.3。
C项中,0.63÷0.01=63。
故答案为:B。
一个小数除以100,就是把小数点向左移动两位;
一个小数乘10,就是把小数点向右移动一位;
一个小数除以0.01,就是把小数点向右移动两位。
13.C
解:三个图形的高相等,设为h,
①的面积:8×h÷2=4h;
②的面积:5×h=5h;
③的面积:(3+6)×h÷2=4.5h;
4h<4.5h<5h,①<③<②。
故答案为:C。
两条平行线之间的距离处处相等,三个图形的高相等,可以设为h,分别表示出三个图形的面积,最后按从小到大的顺序排列。
14.B
解:每种奖券都有,且一等奖的奖券数量最少,则假设只设置了1 张一等奖奖券,此时剩余有39张,又因为二等奖奖券数量既不是最多也不是最少,且三等奖奖券数量最多,所以二等奖奖券最少应该设置2张,此时三等奖奖券数量最多, 有37张。
故答案为:B。
根据题意可知,一等奖的奖券数量应该最小,假设只有1张一等奖奖券,40张奖券还剩39张,剩下的为二等奖和三等奖,二等奖最少可以设置2张,剩下的是三等奖,据此解答。
15.C
解:选项A:数对(2,4)表示第2列第4行,距离方格纸左边边缘2厘米,下边边缘4厘米,都大于等于圆的半径,所以可以以(2,4)为圆心画一个半径是2cm的圆;
选项B:数对(4,2)表示第4列第2行,距离方格纸左边边缘4厘米,下边边缘2厘米,都大于等于圆的半径,所以可以以(4,2)为圆心画一个半径是2cm的圆;
选项C:数对(2,0)表示第2列第0行,距离方格纸左边边缘2厘米,下边边缘0厘米,下边边缘的距离小于2厘米,所以无法以(2,0)为圆心画一个半径是2cm的圆;
选项D:数对(3,4)表示第3列第4行,距离方格纸左边边缘3厘米,下边边缘4厘米,都大于等于圆的半径,所以可以以(3,4)为圆心画一个半径是2cm的圆;
故答案为:C。
在方格纸上画的圆,圆心距离方格纸的边要大于等于半径的长度,据此解答。
16.B
解:直线上M点表示的数可能是算式4.□×4.□的得数。
故答案为:B。
A项中,19×0.9□的结果会更靠近20,而M点在19和20的中间靠近19的位置,所以不合适;
B项中,4.3×4.5=19.35,所以合适;
C项中,19÷1.□<19,所以不合适;
D项中,4×5=20,所以4.□×5.□不合适。
17.B
解:根据题意,可得
2个○=3个△,解得,1个△=
2个△=3个□,解得,1个□=
将1个△=代入1个□=,可得
1个□=
=
所以,9个□=4个○
故答案为:B
根据左边天平,可知,天平的左边有2个○,右边3个△,建立方程:2个○=3个△,求出1个△=;再根据右边天平,可知,天平的左边有2个△,右边有3个□,建立方程:2个△=3个□,求出1个□=,然后再将1个△=代入1个□=,求出□和○的关系,
18.C
解:梯形转化成三角形后,三角形的底是梯形的上下底之和,
54×2÷9=12(厘米)
三角形的底是12厘米。
梯形的面积×2÷梯形的高=梯形的上下底之和。
19.
4.5×0.2=0.9 5x×x=5x2 3.6÷(3.6÷0.4)=0.4
2.56-1.6=0.96 3.2a÷8=0.4a 1.6×0.7÷1.6×0.7=0.49
根据题意,先算乘除、后算加减,有括号的先算括号里面的,据此解答。
20.解:3.25×2.4=7.8
1.8×2.5=4.5
★4.48÷3.2=1.4
验算:
0.568÷3.4≈0.17
计算小数乘法时,先按照整数乘法的计算方法计算出积,然后看两个因数中共有几位小数,就从积的右边向左数出几位点上小数点;除数是小数,先移动除数的小数点,使除数转化成整数,除数的小数点向右移动几位,被除数的小数点也向右移动几位,然后根据除数是整数的除法计算方法计算。
21.(1)解:0.75x-0.5x=25
0.25x=25
x=100
(2)解:
0.2x-0.2×3=1.6
0.2×(x-3)= 1.6
x-3=8
x=11
等式的基本性质1:等式两边同时加上(或减去)同一个整式,等式仍然成立;等式的基本性质2:等式两边同时乘或除以同一个不为0的整式,等式仍然成立;
(1)先将百分数和分数转化为小数,将含有x的式子合并,再等式两边同时除以0.25即可;
(2)将分数和百分数转化为小数,利用乘法结合律将式子化简,再左右两边同时除以0.2,最后等式两边同时加3即可。
22.解:9.2÷0.125÷8
=9.2÷(0.125×8)
=9.2÷1
=9.2
25.25×0.4
=(25+0.25)×0.4
=25×0.4+0.25×0.4
=10+0.1
=10.1
2.021×390+20.21×41+202.1×2
=20.21×39+20.21×41+20.21×20
=20.21×(39+41+20)
=2021
(1)先计算0.125×8,再计算9.2÷1,即可简算出答案,
(2)利用乘法分配律将 25.25拆分成(25+0.25)即可简便计算,
(2)利用小数乘法分配律提取公因数20.21即可简便运算
23.(1)解:
(2)解:=====.......=10,
行驶的路程和耗油量成正比例。因为行驶的路程和耗油量是两种相关联的量,耗油量随行驶路程的变化而变化,且=消耗每升汽油行驶的路程(一定),所以两者成正比例。
(3)解:根据图象推算,这辆汽车行驶350km的耗油量为35L。
(4)解:由(2)可得,消耗每升汽油行驶的路程为10km,
40×10=400(km),
400<460,
所以司机在途中需要加油。
(1)先描点,再连线;
(2)正比例的判断方法:相关联,能变化,商一定;
(3)把射线延长,横轴350千米对应横轴的数是35升,据此解答;
(4)消耗每升汽油行驶的路程×汽油的升数=可以行驶的路程,可以行驶的路程<460千米,在途中需要加油。
24.(1)解:
(2)解:
(3)解:
(4)解:
(1)数对中第一个数表示列,第二个数表示行,根据各点所在的列与行用数对表示,并画出这个长方形;
(2)按1:2缩小后的长方形长是3格,宽是2格,由此画出缩小后的长方形;
(3)缩小后长方形面积是6格,可以画一个底是5格,高是2格的三角形,面积和这个长方形面积相等;
(4)(a,6)在第6行。(1,1)点的北偏东45°方向与第6行的交叉点就是P点的位置。
25.解:因为 是 中点, 为 中点,有 且平行于 ,
则四边形 为梯形.
在梯形 中有③=④,②×⑤=③×④,②:⑤= : =4.
又已知②-⑤=6,
所以⑤= ,②=⑤ ,
所以②×⑤=④×④=16,
而③=④,
所以③=④=4,梯形 的面积为②、③、④、⑤四块图形的面积和,为 .
有 与 的面积比为 平方与 平方的比,即为1:4.
所以 面积为梯形 面积的 = ,即为 .
因为 是 中点,
所以 与 的面积相等,而 的面积为 、 的面积和,即为 平方厘米.
答:三角形 的面积为48平方厘米。
本题主要运用几何的代换将三角形ABC的面积转化为三角形ABD与三角形ADC面积的和,运用了蝴蝶模型的三大性质和等积变形。
26.解:设排数为x,座位号为x+6,
x×(x+6)=216
x=12
或x=﹣18(不合题意,舍去)
12+6=18(号)
答:王老师的电影票是12排18号。
根据题意,可设排数为x,则座位号为x+6,根据题意可得到等量关系式:排数×座位号的乘积是216,把未知数代入等量关系式进行计算即可得到答案。
27.解:(1)(545.1-247.5)÷24.8,要解决的问题是:学校新采购了多少副羽毛球拍?
(2)学校新采购了多少副乒乓球拍?
247.5÷16.5=15(副)
答:学校新采购了15副乒乓球拍。
(1)学校新采购羽毛球拍的副数=(这次买这两种用品共花费的钱数-其中买乒乓球拍用的钱数)÷每副羽毛球拍的单价;
(2)学校新采购乒乓球拍的副数=买乒乓球拍用的钱数÷每副乒乓球拍的单价。
28.(1)原来买120支的总价
(2)原来买120支的钱数现在可以买的支数
解:(1)算式5.5×120解决的问题是:原来买120支的总价;
(2)算式5.5×120÷(5.5-1.5)解决的问题是:原来买120支的钱数现在可以买的支数。
故答案为:(1)原来买120支的总价;(2)原来买120支的钱数现在可以买的支数。
(1)原来买120支的总价=原来的单价×数量;
(2)原来买120支的钱数现在可以买的支数=运来中性笔的单价×原来买的支数÷(运来中性笔的单价-现在每支便宜的钱数)。
29.解:40×2÷(10-8)×(10+8)
=80÷2×18
=40×18
=720(千米)
答:A,B两地相距720千米
同课章节目录
