上海师范大学附属中学2023-2024学年高二下学期期中数学试卷(PDF版,含答案)
文档属性
| 名称 | 上海师范大学附属中学2023-2024学年高二下学期期中数学试卷(PDF版,含答案) |  | |
| 格式 | |||
| 文件大小 | 748.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-09 07:09:39 | ||
图片预览




文档简介
上海师范大学附属中学 2023-2024 学年高二下学期期中数学试卷
一、单选题:本题共 4 小题,共 18 分。在每小题给出的选项中,只有一项是符合题目要求的。
1.下表是“膜法世家”形象代言人选举得票情况统计,其中周柯宇的票数被污损了无法看清,那么应该当
选的人是( )
姓名 张元英 林正英 米卡 周柯宇 林墨 合计
票数 250 200 380 ■ 320 1550
A. 米卡 B. 周柯宇 C. 无法确定 D. 合计
2.高考数学试题中,有12道选择题,每道选择题有4个选项,其中只有1个选项是正确的,则随机选择其中
1
一个选项,正确的概率是 ,某家长说:“要是都不会做,每题都随机选择其中1个选项,则一定有3道题答
4
对.”这句话( )
A. 正确 B. 错误 C. 不一定 D. 无法解释
3.如图,在下列各正方体中, 为正方体的一条体对角线, 、 分别为所在棱的中点,则满足 ⊥ 的是( )
A. B.
C. D.
4.已知 , 为同一次试验中的两个随机事件,且 ( ) > 0, ( ) > 0,命题甲:若 ( | ) + ( ) = 1,则
事件 与 相互独立;命题乙:“ 与 相互独立”是“ ( | ) = ( | )”的充分不必要条件;则命题( )
A. 甲乙都是真命题 B. 甲是真命题,乙是假命题
C. 甲是假命题,乙是真命题 D. 甲乙都是假命题
二、填空题:本题共 12 小题,共 54 分。
5.某读书会有5名成员,假期他们每个人阅读的本数分别如下:3,5,4,2,1,则这组数据的60%分位数
为______.
第 1 页,共 12 页
6.一个圆锥的侧面积是其底面积的2倍,则该圆锥的母线与底面所成的角为 .
7.已知 4 = 4 +1 +
5
( ∈
),则 = ______.
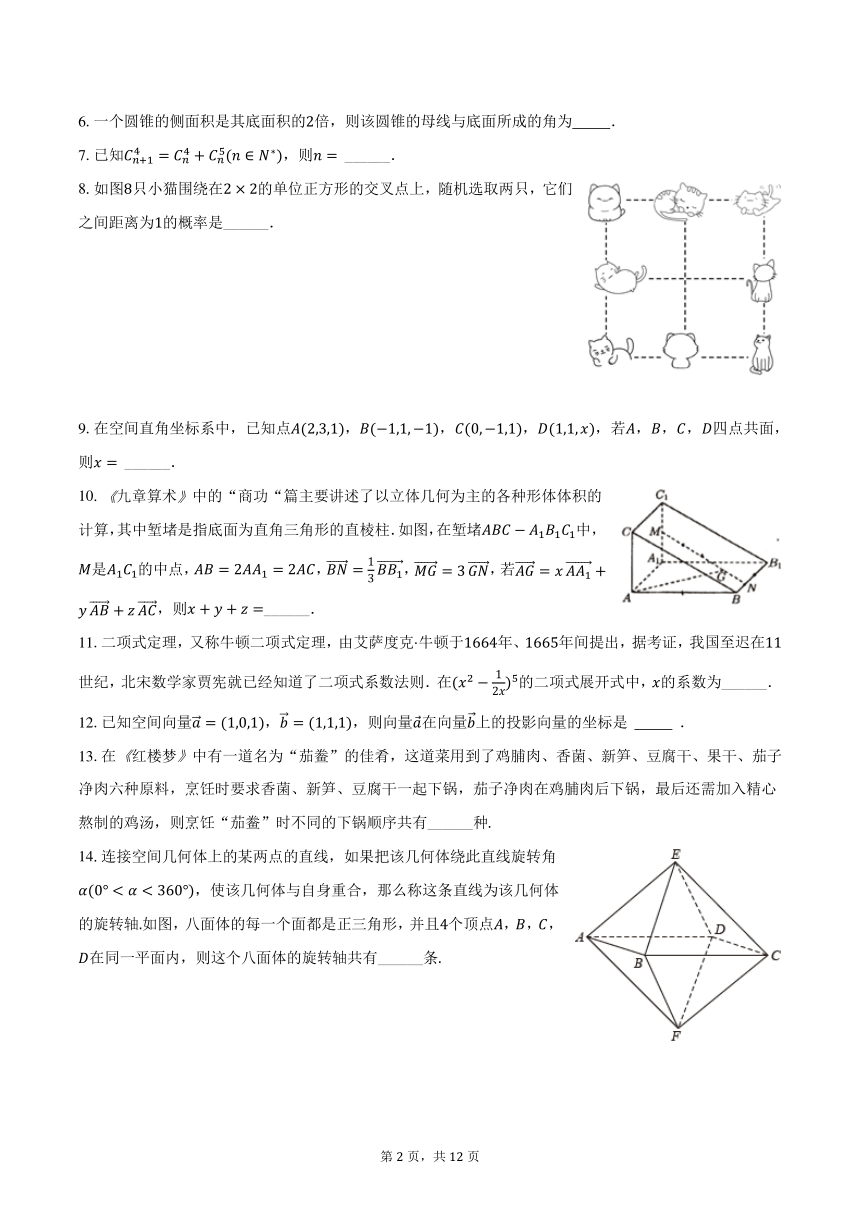
8.如图8只小猫围绕在2 × 2的单位正方形的交叉点上,随机选取两只,它们
之间距离为1的概率是______.
9.在空间直角坐标系中,已知点 (2,3,1), ( 1,1, 1), (0, 1,1), (1,1, ),若 , , , 四点共面,
则 = ______.
10.《九章算术》中的“商功“篇主要讲述了以立体几何为主的各种形体体积的
计算,其中堑堵是指底面为直角三角形的直棱柱.如图,在堑堵 1 1 1中,
1
是 1 1的中点, = 2 1 = 2 , = 1, = 3 ,若 = +3 1
+ ,则 + + =______.
11.二项式定理,又称牛顿二项式定理,由艾萨度克 牛顿于1664年、1665年间提出,据考证,我国至迟在11
1
世纪,北宋数学家贾宪就已经知道了二项式系数法则.在( 2 )5的二项式展开式中, 的系数为______.
2
12.已知空间向量 = (1,0,1), = (1,1,1),则向量 在向量 上的投影向量的坐标是 .
13.在《红楼梦》中有一道名为“茄鲞”的佳肴,这道菜用到了鸡脯肉、香菌、新笋、豆腐干、果干、茄子
净肉六种原料,烹饪时要求香菌、新笋、豆腐干一起下锅,茄子净肉在鸡脯肉后下锅,最后还需加入精心
熬制的鸡汤,则烹饪“茄鲞”时不同的下锅顺序共有______种.
14.连接空间几何体上的某两点的直线,如果把该几何体绕此直线旋转角
(0° < < 360°),使该几何体与自身重合,那么称这条直线为该几何体
的旋转轴.如图,八面体的每一个面都是正三角形,并且4个顶点 , , ,
在同一平面内,则这个八面体的旋转轴共有______条.
第 2 页,共 12 页
15.设样本空间 = 1,2,3,4,5,6,7,8的样本点都是等可能出现的,且事件 = {1,2,3,4},事件 = {1,2,3,5},
事件 = {1, , , 8},使得 ( ) = ( ) ( ) ( ),且满足 , , 两两不独立,则 + = ______.
16.已知正四面体 的棱长为2,动点 满足 = 0,且 = 0,则点 的轨迹长为______.
三、解答题:本题共 5 小题,共 78 分。解答应写出文字说明,证明过程或演算步骤。
17.(本小题14分)
先后抛掷一枚质地均匀的骰子两次,记向上的点数分别为 , ,将事件“log( +1) 为整数”记为 ,将事件
“ + 为偶数”记为 ,将事件“ + 2 为奇数”记为 .
(1)试判断事件 与事件 是否相互独立?并说明理由;
(2)求 ( | )的值.
18.(本小题14分)
已知甲组数据 1, 2,…, 15的茎叶图如图所示,其中数据的整数部分为茎,数据的小数部分(仅一位小数
)为叶,例如第一个数据为5.3.
(1)甲组数据的平均值 、方差 21 1、中位数 ;
(2)乙组数据为 1, 2,…, 15,且甲、乙两组数据合并后的30个数据的平均值 = 9.2,方差
2 = 11.23,
求乙组数据的平均值 2和方差
2
2,写出必要的计算过程和步骤.
19.(本小题14分)
某企业为了了解本企业员工每天慢走与慢跑的情况,对每天慢走时间在25分钟到55分钟之间的员工,随机
抽取 人进行调查,将既参加慢走又参加慢跑的人称为“ 族”,否则称为“非 族”,得如下的统计表以
及每天慢走时间在25分钟到55分钟之间的员工人数的频率分布直方图(部分):
第 3 页,共 12 页
组数 分组 人数 本组中“ 族”的比例
1 [25,30) 200 0.6
2 [30,35) 300 0.65
3 [35,40) 200 0.5
4 [40,45) 150 0.4
5 [45,50) 0.3
6 [50,55) 50 0.3
(1)试补全频率分布直方图,并求 与 的值:
(2)从每天慢走时间在[40,50)(分钟)内的“ 族”中按时间采用分层抽样法抽取6人参加企业举办的健身沙
龙体验活动,再从这6人中选2人作健身技巧与减脂秘籍的发言,求这2人每天慢走的时间恰好1人在[40,45)
分钟内,另一个人在[45,50)分钟内的概率.
20.(本小题18分)
如图所示的空间直角坐标系 中,所有坐标均为整数的点称为整点;已知正方体 1 1 1 1的
棱长为 ,点 满足 = + 1,其中 ∈ [0,1], ∈ [0,1].
(1)若 = 1,且直线 1 与平面 1 1 所成角大小为 ,求点 的轨迹长度; 4
(2)若 = 1, = 1,求正方体经过点 1, , 的截面面积 的取值范围;
(3)若 = 8,求三棱锥 1 内(不包括表面边界)整点的个数.
第 4 页,共 12 页
21.(本小题18分)
高斯是德国著名的数学家,近代数学奠基者之一,享有“数学王子”的称号,他和阿基米德、牛顿并列为
世界三大数学家,为了纪念他,人们把函数 = [ ]( ∈ )称为高斯函数,其中[ ]表示不超过 的最大整数.
已知: ( ) = ( + √ 3)
,( ∈ , ≥ 1)
(1)若 ( 1) = + √ 3 , , ∈ ,求 4 + 4的值;
(2)若 (1) = + √ 3 , , ∈ ,求证:
2
2 3
2
2 = 4 ;
(3)设 = ∑2024
2024 +2024
=1 [ ],求 除以2023的余数.
( 1) 2023
第 5 页,共 12 页
1.【答案】
2.【答案】
3.【答案】
4.【答案】
5.【答案】3.5
6.【答案】60°
7.【答案】8
2
8.【答案】
7
9.【答案】1
11
10.【答案】
8
5
11.【答案】
4
2 2 2
12.【答案】( , , )
3 3 3
13.【答案】12
14.【答案】13
15.【答案】13
16.【答案】√ 3
17.【答案】解:(1)先后两次抛掷一枚质地均匀的骰子,得到向上的点数分别为 , ,
则基本事件总数为(1,1),(1,2),(1,3),(1,4),(1,5),(1,6),
(2,1),(2,2),(2,3),(2,4),(2,5),(2,6),
(3,1),(3,2),(3,3),(3,4),(3,5),(3,6),
(4,1),(4,2),(4,3),(4,4),(4,5),(4,6),
(5,1),(5,2),(5,3),(5,4),(5,5),(5,6),
(6,1),(6,2),(6,3),(6,4),(6,5),(6,6),共36种情况,
满足事件 的有(1,1),(1,3),(1,5),(2,2),(2,4),(2,6),(3,1),(3,3),(3,5),(3,6),(4,2),(4,4),(4,6),
(5,1),(5,3),(5,5),(6,2),(6,4),(6,6),共18个,
18 1
故 ( ) = = ,
36 2
满足事件 的有(1,1),(1,2),(1,3),(1,4),(1,5),(1,6),(3,1),(3,2),(3,3),(3,4),(3,5),(3,6),(5,1),
第 6 页,共 12 页
(5,2),(5,3),(5,4),(5,5),(5,6),共18个,
18 1
故 ( ) = = ,
36 2
满足事件 的有(1,1),(1,3),(1,5),(3,1),(3,3),(3,5),(5,1),(5,3),(5,5),共9个,
9 1
所以 ( ) = = = ( ) ( ),
36 4
所以事件 与事件 相互独立;
(2)满足事件 的有(1,1),(1,2),(1,4),(3,1),(3,4),(5,6),(5,1),共7种,
7
所以 ( ) = ,
36
7
( ) 7
所以 ( | ) = = 36 = ,
( ) 1 18
2
18.【答案】解:(1)甲组数据为5.3,6.5,7.4,7.6,8.1,8.1,8.1,8.2,8.2,8.4,9.5,9.8,10.5,11.0,
13.8,
所以甲组数据的中位数为 = 8.2,
1
甲组数据的平均值为 1 = (5.3 + 6.5 + 7.4 + 7.6 + 8.1 × 3 + 8.2 × 2 + 8.4 + 9.5 + 9.8 + 10.5 + 11.0 +15
13.8) = 8.7.
1
甲组数据的方差为 2 21 = [(5.3 8.7) + (6.5 8.7)
2 + (7.4 8.7)2 + (7.6 8.7)2 + (8.1 8.7)2 × 3 +
15
(8.2 8.7)2 × 2 + (8.4 8.7)2 + (9.5 8.7)2 + (9.8 8.7)2 + (10.5 8.7)2 + (11.0 8.7)2 + (13.8
8.7)2] = 3.824.
15×8.7+15
(2)由 2 = 9.2,可得 = 9.7,
30 2
1
∑15 2 2
15 =1
8.7 = 3.824
由{ ,解得∑15 2 = 1192.71,∑15 2
1
= 1683.39,
(∑15 2
=1 =1
=1 + ∑
15 2 2 =1 ) 9.2 = 11.2330
1
所以 2 = ∑15 2
1
2 =1 9.7
2 = × 1683.39 9.72 = 18.136.
15 15
19.【答案】解:(1)第二组的频率为1 (0.04 + 0.04 + 0.03 + 0.02 + 0.01) × 5 = 0.3,
0.3
所以第二组小矩形高为 = 0.06.补全后的频率直方图如下:
5
第 7 页,共 12 页
200
第一组的频率为0.04 × 5 = 0.2,所以 = = 1000.
0.2
第五组的频率为0.02 × 5 = 0.1,所以 = 1000 × 0.1 = 100.
(2)因为[40,50)分钟的“ 族”人数为150 × 0.4 = 60,
[45,50)分钟的“ 族”人数为100 × 0.3 = 30,二者比例为60:30 = 2:1,
所以按时间采用分层抽样法抽取6人,[40,45)分钟内抽取4人,[45,50)分钟内抽取2人.
设这2人每天慢走的时间恰好1人在[40,45)分钟,另一个人在[45,50)分钟为事件 ,
在[40,45)分钟内抽取4人记为 , , , ,[45,50)分钟内抽取2人记为 , ,
则有 , , , , , , , , , , , , , , ,
共15种不同的抽取方法,事件 有 , , , , , , , ,共8种,
8
所以 ( ) = ,即选出发言的2人每天慢走的时间恰好1人在[40,45)分钟内,
15
8
另一个人在[45,50)分钟内的概率为 .
15
20.【答案】解:(1)空间直角坐标系 中,所有坐标均为整数的点称为整点,
正方体 1 1 1 1的棱长为 ,点 满足 = + 1,其中 ∈ [0,1], ∈ [0,1],
连接 1 ,
∵ 1 1 ⊥平面 1 1, 1 为 1 在平面 1 1上的射影,
∴直线 1 与平面 1 1 所成角的平面角为∠ 1 1,
由已知∠ 1 1 = , 4
第 8 页,共 12 页
1
则 1 = 1 1 = 1,故 点轨迹为以 1为圆心,1为半径的 圆在正方形 4 1
1 内的部分,
1
∴点 的轨迹长度为 × 2 × 1 = ,
4 2
(2)在正方体 1 1 1 1中,以 为坐标原点,
以 , , 1所在的直线分别为 , , 轴建立空间直角坐标系,
∵ = 1,
∴ (1,1,0), (0,1,0), 1(1,1,1), 1(0,0,1),
∵ = + 1, = 1,
∴ = + ,即 1 = 1,
∴ 点在 1上运动,则 (0,1, ),
过点 1作 1 // ,交 1与点 ,连接 ,
∵平面 1 1//平面 1 1,
平面 1 1 ∩平面 1 = ,平面 1 1 ∩平面 1 = 1 ,
∴ // 1 ,又 1 // ,
∴在正方体中经过点 1, , 的截面为平行四边形 1 ,如图,
则 = (1,0, ), 1 = (1,1, 1),
∴点 到 1 的距离为:
第 9 页,共 12 页
2 1
2 2 1+ 2 √ 2
2 2 +2
= √ | | ( ) = √ 1 + ( ) = ,
| 1 | √ 3 3
∵ ∈ [0,1],故当 取0或1时, 取到最大值 2√ ,
3
此时截面面积的最大值为 1 22 △ = 2 × × √ 3 × √ = √ 2, 1 2 3
1
当 时, 取到最小值√ 2 = ,
2 2
1 √ 2 √ 6
此时截面面积的最小值为2 △ = 2 × × √ 3 × = , 1 2 2 2
∴当 = 1
√ 6
时,在正方体中经过点 1, , 的截面面积的取值范围为[ , √ 2]. 2
(3)如图,过 轴上的点 2(0,0,7), 3(0,0,6), 4(0,0,5), 5(0,0,4), 6(0,0,3),
7(0,0,2), 8(0,0,1),作三棱锥 1 平行于底面 的截面,
则三棱锥 1 内(不包括表面边界)整点一定位于各截面内,
截面 2 2 2内的整点个数为0,
截面 3 3 3内的整点个数为0,
截面 4 4 4内的整点有1个,为(1,1,5),
截面 5 5 5内的整点有3个,分别为:(1,1,4),(1,2,4),(2,1,4),
截面 6 6 6内的整点有6个,分别为:(1,1,3),(1,2,3),(1,3,3),(2,1,3),(2,2,3),(3,1,3),
截面 7 7 7内的整点有10个,分别为:
(1,1,2),(1,2,2),(1,3,2),(1,4,2),(2,1,2),(2,2,2),(2,3,2),
(3,1,2),(3,2,2),(4,1,2),
截面 8 8 8内的整点有15个,分别为:
第 10 页,共 12 页
(1,1,1),(1,2,1),(1,3,1),(1,4,1),(1,5,1),(2,1,1),(2,2,1),
(2,3,1),(2,4,1),(3,1,1),(3,2,1),(3,3,1),(4,1,1),(4,2,1),(5,1,1),
∴三棱锥 1 内(不包括表面边界)整点个数为35.
21.【答案】解:(1)因为 ( 1) =
+ √ 3 , ( ) = ( + √ 3) ,
所以当 = 4时, 44( 1) = ( 1 + √ 3) = 4 + √ 3 4,
而( 1 + √ 3)4 = ( 1 + √ 3)2( 1 + √ 3)2 = (4 2√ 3)2 = 28 16√ 3,
因为 , ∈ , 4 + √ 3 4 = 28 16√ 3,
所以 4 = 28, 4 = 16, 4 + 4 = 28 16 = 12.
(2)因为 ( ) = ( + √ 3)
, (1) = + √ 3 , , ∈ ,
则 22 3
2
2 = ( 2 √ 3 2 )( 2 + √ 3 2 ) = (1 √ 3)
2 (1 + √ 3)2 = [(1 √ 3)(1 + √ 3)]2 =
( 2)2 = 4 .
故 2 3 2 = 4 2 2 .
2024 +2024 (2023+1) +2023 +
(3) = = ,
( 1) 2023 ( 1) 2023
又(2023 + 1) = 02023 + 1 2023
1 + + 1 2023 +
0
2023 ,
(2023+1) 1
则 = 0 2023
1 + 1 2023
2 + + 1 + ,
2023 2023
2024
又 = + ,
2023 2023
2024 +2024
所以 = 02023 1 1
1
+ 2023
2 + + 1 + + + =
02023 1 + 12023 2 +
2023 2023 2023
1 +1+ + + , 2023
所以当 = 2 ,(1 ≤ ≤ 1010, ∈ ),
2024 +2024 20242 +2024 2
[ ] = [ ]
( 1) 2023 2023
= [ 0 20232 1 + 1 20232 2 + + 2 1
2 +1
+ 2 + ] = 0 20232 1 + 1 20232 2 + + 2 12 2 2 2 2 2 + 2 , 2023
其除以2023的余数为 2 12 + 2 = 2 + 2 = 4 ,
当 = 2 ,( = 1011, = 1012)时,
2024 +2024 20242 +2024 2
[ ] = [ ] = [ 0 2 1 1 2 2 2 1
2 +1
2023 2
2023 + 2 2023 + + 2 + 2 + ] =
( 1) 2023 2023
0 20232 1 + 1 2 2 2 12 2 2023 + + 2 + 2 + 1,
其除以2023的余数2022和3,
当1 ≤ ≤ 2024且 = 2 1,(1 ≤ ≤ 1011, ∈ )时,
第 11 页,共 12 页
2024 +2024 20242 1+2024 (2 1)
[ ] = [ ( )] = [ (
0
2 12023
2 2 + 1 2 3 2 2
2023 2 1
2023 + + 2 1 + 2 1 +
( 1) 2023
2
)] = ( 02 12023
2 2 + 1 2 32 12023 + +
2 2
2023 2 1
+ 2 ),
其除以2023的余数为2023 (4 1) = 2024 4 ,
当 = 2 1, = 1012时,
2024 +2024 20242 1+2024 (2 1)
[ 0 ] = [ ( )] = [ ( 2 12023
2 2 + 1 2 3 2 2
2023 2 1
2023 + + 2 1 + 2 1 +
( 1) 2023
2
)] = ( 0 20232 2 + 1 2 3 2 2
2023 2 1 2 1
2023 + + 2 1 + 2 + 1),
其除以2023的余数为2021,
除以2023的余数为∑1011( 4 ) + 2022 + 3 + ∑1011 =1 =1 ( 2024 4 ) + 2021除以2023的余数,
即2024 × 1011 + 2022 + 3 + 2021 = 2024 × 1011 + 4046除以2023的余数,
又2024 × 1011 + 4046 = (2023 + 1) × 1011 + 2023 × 2 = 2023 × 1011 + 1011 + 2023 × 2其除以2023的
余数为1011.
第 12 页,共 12 页
一、单选题:本题共 4 小题,共 18 分。在每小题给出的选项中,只有一项是符合题目要求的。
1.下表是“膜法世家”形象代言人选举得票情况统计,其中周柯宇的票数被污损了无法看清,那么应该当
选的人是( )
姓名 张元英 林正英 米卡 周柯宇 林墨 合计
票数 250 200 380 ■ 320 1550
A. 米卡 B. 周柯宇 C. 无法确定 D. 合计
2.高考数学试题中,有12道选择题,每道选择题有4个选项,其中只有1个选项是正确的,则随机选择其中
1
一个选项,正确的概率是 ,某家长说:“要是都不会做,每题都随机选择其中1个选项,则一定有3道题答
4
对.”这句话( )
A. 正确 B. 错误 C. 不一定 D. 无法解释
3.如图,在下列各正方体中, 为正方体的一条体对角线, 、 分别为所在棱的中点,则满足 ⊥ 的是( )
A. B.
C. D.
4.已知 , 为同一次试验中的两个随机事件,且 ( ) > 0, ( ) > 0,命题甲:若 ( | ) + ( ) = 1,则
事件 与 相互独立;命题乙:“ 与 相互独立”是“ ( | ) = ( | )”的充分不必要条件;则命题( )
A. 甲乙都是真命题 B. 甲是真命题,乙是假命题
C. 甲是假命题,乙是真命题 D. 甲乙都是假命题
二、填空题:本题共 12 小题,共 54 分。
5.某读书会有5名成员,假期他们每个人阅读的本数分别如下:3,5,4,2,1,则这组数据的60%分位数
为______.
第 1 页,共 12 页
6.一个圆锥的侧面积是其底面积的2倍,则该圆锥的母线与底面所成的角为 .
7.已知 4 = 4 +1 +
5
( ∈
),则 = ______.
8.如图8只小猫围绕在2 × 2的单位正方形的交叉点上,随机选取两只,它们
之间距离为1的概率是______.
9.在空间直角坐标系中,已知点 (2,3,1), ( 1,1, 1), (0, 1,1), (1,1, ),若 , , , 四点共面,
则 = ______.
10.《九章算术》中的“商功“篇主要讲述了以立体几何为主的各种形体体积的
计算,其中堑堵是指底面为直角三角形的直棱柱.如图,在堑堵 1 1 1中,
1
是 1 1的中点, = 2 1 = 2 , = 1, = 3 ,若 = +3 1
+ ,则 + + =______.
11.二项式定理,又称牛顿二项式定理,由艾萨度克 牛顿于1664年、1665年间提出,据考证,我国至迟在11
1
世纪,北宋数学家贾宪就已经知道了二项式系数法则.在( 2 )5的二项式展开式中, 的系数为______.
2
12.已知空间向量 = (1,0,1), = (1,1,1),则向量 在向量 上的投影向量的坐标是 .
13.在《红楼梦》中有一道名为“茄鲞”的佳肴,这道菜用到了鸡脯肉、香菌、新笋、豆腐干、果干、茄子
净肉六种原料,烹饪时要求香菌、新笋、豆腐干一起下锅,茄子净肉在鸡脯肉后下锅,最后还需加入精心
熬制的鸡汤,则烹饪“茄鲞”时不同的下锅顺序共有______种.
14.连接空间几何体上的某两点的直线,如果把该几何体绕此直线旋转角
(0° < < 360°),使该几何体与自身重合,那么称这条直线为该几何体
的旋转轴.如图,八面体的每一个面都是正三角形,并且4个顶点 , , ,
在同一平面内,则这个八面体的旋转轴共有______条.
第 2 页,共 12 页
15.设样本空间 = 1,2,3,4,5,6,7,8的样本点都是等可能出现的,且事件 = {1,2,3,4},事件 = {1,2,3,5},
事件 = {1, , , 8},使得 ( ) = ( ) ( ) ( ),且满足 , , 两两不独立,则 + = ______.
16.已知正四面体 的棱长为2,动点 满足 = 0,且 = 0,则点 的轨迹长为______.
三、解答题:本题共 5 小题,共 78 分。解答应写出文字说明,证明过程或演算步骤。
17.(本小题14分)
先后抛掷一枚质地均匀的骰子两次,记向上的点数分别为 , ,将事件“log( +1) 为整数”记为 ,将事件
“ + 为偶数”记为 ,将事件“ + 2 为奇数”记为 .
(1)试判断事件 与事件 是否相互独立?并说明理由;
(2)求 ( | )的值.
18.(本小题14分)
已知甲组数据 1, 2,…, 15的茎叶图如图所示,其中数据的整数部分为茎,数据的小数部分(仅一位小数
)为叶,例如第一个数据为5.3.
(1)甲组数据的平均值 、方差 21 1、中位数 ;
(2)乙组数据为 1, 2,…, 15,且甲、乙两组数据合并后的30个数据的平均值 = 9.2,方差
2 = 11.23,
求乙组数据的平均值 2和方差
2
2,写出必要的计算过程和步骤.
19.(本小题14分)
某企业为了了解本企业员工每天慢走与慢跑的情况,对每天慢走时间在25分钟到55分钟之间的员工,随机
抽取 人进行调查,将既参加慢走又参加慢跑的人称为“ 族”,否则称为“非 族”,得如下的统计表以
及每天慢走时间在25分钟到55分钟之间的员工人数的频率分布直方图(部分):
第 3 页,共 12 页
组数 分组 人数 本组中“ 族”的比例
1 [25,30) 200 0.6
2 [30,35) 300 0.65
3 [35,40) 200 0.5
4 [40,45) 150 0.4
5 [45,50) 0.3
6 [50,55) 50 0.3
(1)试补全频率分布直方图,并求 与 的值:
(2)从每天慢走时间在[40,50)(分钟)内的“ 族”中按时间采用分层抽样法抽取6人参加企业举办的健身沙
龙体验活动,再从这6人中选2人作健身技巧与减脂秘籍的发言,求这2人每天慢走的时间恰好1人在[40,45)
分钟内,另一个人在[45,50)分钟内的概率.
20.(本小题18分)
如图所示的空间直角坐标系 中,所有坐标均为整数的点称为整点;已知正方体 1 1 1 1的
棱长为 ,点 满足 = + 1,其中 ∈ [0,1], ∈ [0,1].
(1)若 = 1,且直线 1 与平面 1 1 所成角大小为 ,求点 的轨迹长度; 4
(2)若 = 1, = 1,求正方体经过点 1, , 的截面面积 的取值范围;
(3)若 = 8,求三棱锥 1 内(不包括表面边界)整点的个数.
第 4 页,共 12 页
21.(本小题18分)
高斯是德国著名的数学家,近代数学奠基者之一,享有“数学王子”的称号,他和阿基米德、牛顿并列为
世界三大数学家,为了纪念他,人们把函数 = [ ]( ∈ )称为高斯函数,其中[ ]表示不超过 的最大整数.
已知: ( ) = ( + √ 3)
,( ∈ , ≥ 1)
(1)若 ( 1) = + √ 3 , , ∈ ,求 4 + 4的值;
(2)若 (1) = + √ 3 , , ∈ ,求证:
2
2 3
2
2 = 4 ;
(3)设 = ∑2024
2024 +2024
=1 [ ],求 除以2023的余数.
( 1) 2023
第 5 页,共 12 页
1.【答案】
2.【答案】
3.【答案】
4.【答案】
5.【答案】3.5
6.【答案】60°
7.【答案】8
2
8.【答案】
7
9.【答案】1
11
10.【答案】
8
5
11.【答案】
4
2 2 2
12.【答案】( , , )
3 3 3
13.【答案】12
14.【答案】13
15.【答案】13
16.【答案】√ 3
17.【答案】解:(1)先后两次抛掷一枚质地均匀的骰子,得到向上的点数分别为 , ,
则基本事件总数为(1,1),(1,2),(1,3),(1,4),(1,5),(1,6),
(2,1),(2,2),(2,3),(2,4),(2,5),(2,6),
(3,1),(3,2),(3,3),(3,4),(3,5),(3,6),
(4,1),(4,2),(4,3),(4,4),(4,5),(4,6),
(5,1),(5,2),(5,3),(5,4),(5,5),(5,6),
(6,1),(6,2),(6,3),(6,4),(6,5),(6,6),共36种情况,
满足事件 的有(1,1),(1,3),(1,5),(2,2),(2,4),(2,6),(3,1),(3,3),(3,5),(3,6),(4,2),(4,4),(4,6),
(5,1),(5,3),(5,5),(6,2),(6,4),(6,6),共18个,
18 1
故 ( ) = = ,
36 2
满足事件 的有(1,1),(1,2),(1,3),(1,4),(1,5),(1,6),(3,1),(3,2),(3,3),(3,4),(3,5),(3,6),(5,1),
第 6 页,共 12 页
(5,2),(5,3),(5,4),(5,5),(5,6),共18个,
18 1
故 ( ) = = ,
36 2
满足事件 的有(1,1),(1,3),(1,5),(3,1),(3,3),(3,5),(5,1),(5,3),(5,5),共9个,
9 1
所以 ( ) = = = ( ) ( ),
36 4
所以事件 与事件 相互独立;
(2)满足事件 的有(1,1),(1,2),(1,4),(3,1),(3,4),(5,6),(5,1),共7种,
7
所以 ( ) = ,
36
7
( ) 7
所以 ( | ) = = 36 = ,
( ) 1 18
2
18.【答案】解:(1)甲组数据为5.3,6.5,7.4,7.6,8.1,8.1,8.1,8.2,8.2,8.4,9.5,9.8,10.5,11.0,
13.8,
所以甲组数据的中位数为 = 8.2,
1
甲组数据的平均值为 1 = (5.3 + 6.5 + 7.4 + 7.6 + 8.1 × 3 + 8.2 × 2 + 8.4 + 9.5 + 9.8 + 10.5 + 11.0 +15
13.8) = 8.7.
1
甲组数据的方差为 2 21 = [(5.3 8.7) + (6.5 8.7)
2 + (7.4 8.7)2 + (7.6 8.7)2 + (8.1 8.7)2 × 3 +
15
(8.2 8.7)2 × 2 + (8.4 8.7)2 + (9.5 8.7)2 + (9.8 8.7)2 + (10.5 8.7)2 + (11.0 8.7)2 + (13.8
8.7)2] = 3.824.
15×8.7+15
(2)由 2 = 9.2,可得 = 9.7,
30 2
1
∑15 2 2
15 =1
8.7 = 3.824
由{ ,解得∑15 2 = 1192.71,∑15 2
1
= 1683.39,
(∑15 2
=1 =1
=1 + ∑
15 2 2 =1 ) 9.2 = 11.2330
1
所以 2 = ∑15 2
1
2 =1 9.7
2 = × 1683.39 9.72 = 18.136.
15 15
19.【答案】解:(1)第二组的频率为1 (0.04 + 0.04 + 0.03 + 0.02 + 0.01) × 5 = 0.3,
0.3
所以第二组小矩形高为 = 0.06.补全后的频率直方图如下:
5
第 7 页,共 12 页
200
第一组的频率为0.04 × 5 = 0.2,所以 = = 1000.
0.2
第五组的频率为0.02 × 5 = 0.1,所以 = 1000 × 0.1 = 100.
(2)因为[40,50)分钟的“ 族”人数为150 × 0.4 = 60,
[45,50)分钟的“ 族”人数为100 × 0.3 = 30,二者比例为60:30 = 2:1,
所以按时间采用分层抽样法抽取6人,[40,45)分钟内抽取4人,[45,50)分钟内抽取2人.
设这2人每天慢走的时间恰好1人在[40,45)分钟,另一个人在[45,50)分钟为事件 ,
在[40,45)分钟内抽取4人记为 , , , ,[45,50)分钟内抽取2人记为 , ,
则有 , , , , , , , , , , , , , , ,
共15种不同的抽取方法,事件 有 , , , , , , , ,共8种,
8
所以 ( ) = ,即选出发言的2人每天慢走的时间恰好1人在[40,45)分钟内,
15
8
另一个人在[45,50)分钟内的概率为 .
15
20.【答案】解:(1)空间直角坐标系 中,所有坐标均为整数的点称为整点,
正方体 1 1 1 1的棱长为 ,点 满足 = + 1,其中 ∈ [0,1], ∈ [0,1],
连接 1 ,
∵ 1 1 ⊥平面 1 1, 1 为 1 在平面 1 1上的射影,
∴直线 1 与平面 1 1 所成角的平面角为∠ 1 1,
由已知∠ 1 1 = , 4
第 8 页,共 12 页
1
则 1 = 1 1 = 1,故 点轨迹为以 1为圆心,1为半径的 圆在正方形 4 1
1 内的部分,
1
∴点 的轨迹长度为 × 2 × 1 = ,
4 2
(2)在正方体 1 1 1 1中,以 为坐标原点,
以 , , 1所在的直线分别为 , , 轴建立空间直角坐标系,
∵ = 1,
∴ (1,1,0), (0,1,0), 1(1,1,1), 1(0,0,1),
∵ = + 1, = 1,
∴ = + ,即 1 = 1,
∴ 点在 1上运动,则 (0,1, ),
过点 1作 1 // ,交 1与点 ,连接 ,
∵平面 1 1//平面 1 1,
平面 1 1 ∩平面 1 = ,平面 1 1 ∩平面 1 = 1 ,
∴ // 1 ,又 1 // ,
∴在正方体中经过点 1, , 的截面为平行四边形 1 ,如图,
则 = (1,0, ), 1 = (1,1, 1),
∴点 到 1 的距离为:
第 9 页,共 12 页
2 1
2 2 1+ 2 √ 2
2 2 +2
= √ | | ( ) = √ 1 + ( ) = ,
| 1 | √ 3 3
∵ ∈ [0,1],故当 取0或1时, 取到最大值 2√ ,
3
此时截面面积的最大值为 1 22 △ = 2 × × √ 3 × √ = √ 2, 1 2 3
1
当 时, 取到最小值√ 2 = ,
2 2
1 √ 2 √ 6
此时截面面积的最小值为2 △ = 2 × × √ 3 × = , 1 2 2 2
∴当 = 1
√ 6
时,在正方体中经过点 1, , 的截面面积的取值范围为[ , √ 2]. 2
(3)如图,过 轴上的点 2(0,0,7), 3(0,0,6), 4(0,0,5), 5(0,0,4), 6(0,0,3),
7(0,0,2), 8(0,0,1),作三棱锥 1 平行于底面 的截面,
则三棱锥 1 内(不包括表面边界)整点一定位于各截面内,
截面 2 2 2内的整点个数为0,
截面 3 3 3内的整点个数为0,
截面 4 4 4内的整点有1个,为(1,1,5),
截面 5 5 5内的整点有3个,分别为:(1,1,4),(1,2,4),(2,1,4),
截面 6 6 6内的整点有6个,分别为:(1,1,3),(1,2,3),(1,3,3),(2,1,3),(2,2,3),(3,1,3),
截面 7 7 7内的整点有10个,分别为:
(1,1,2),(1,2,2),(1,3,2),(1,4,2),(2,1,2),(2,2,2),(2,3,2),
(3,1,2),(3,2,2),(4,1,2),
截面 8 8 8内的整点有15个,分别为:
第 10 页,共 12 页
(1,1,1),(1,2,1),(1,3,1),(1,4,1),(1,5,1),(2,1,1),(2,2,1),
(2,3,1),(2,4,1),(3,1,1),(3,2,1),(3,3,1),(4,1,1),(4,2,1),(5,1,1),
∴三棱锥 1 内(不包括表面边界)整点个数为35.
21.【答案】解:(1)因为 ( 1) =
+ √ 3 , ( ) = ( + √ 3) ,
所以当 = 4时, 44( 1) = ( 1 + √ 3) = 4 + √ 3 4,
而( 1 + √ 3)4 = ( 1 + √ 3)2( 1 + √ 3)2 = (4 2√ 3)2 = 28 16√ 3,
因为 , ∈ , 4 + √ 3 4 = 28 16√ 3,
所以 4 = 28, 4 = 16, 4 + 4 = 28 16 = 12.
(2)因为 ( ) = ( + √ 3)
, (1) = + √ 3 , , ∈ ,
则 22 3
2
2 = ( 2 √ 3 2 )( 2 + √ 3 2 ) = (1 √ 3)
2 (1 + √ 3)2 = [(1 √ 3)(1 + √ 3)]2 =
( 2)2 = 4 .
故 2 3 2 = 4 2 2 .
2024 +2024 (2023+1) +2023 +
(3) = = ,
( 1) 2023 ( 1) 2023
又(2023 + 1) = 02023 + 1 2023
1 + + 1 2023 +
0
2023 ,
(2023+1) 1
则 = 0 2023
1 + 1 2023
2 + + 1 + ,
2023 2023
2024
又 = + ,
2023 2023
2024 +2024
所以 = 02023 1 1
1
+ 2023
2 + + 1 + + + =
02023 1 + 12023 2 +
2023 2023 2023
1 +1+ + + , 2023
所以当 = 2 ,(1 ≤ ≤ 1010, ∈ ),
2024 +2024 20242 +2024 2
[ ] = [ ]
( 1) 2023 2023
= [ 0 20232 1 + 1 20232 2 + + 2 1
2 +1
+ 2 + ] = 0 20232 1 + 1 20232 2 + + 2 12 2 2 2 2 2 + 2 , 2023
其除以2023的余数为 2 12 + 2 = 2 + 2 = 4 ,
当 = 2 ,( = 1011, = 1012)时,
2024 +2024 20242 +2024 2
[ ] = [ ] = [ 0 2 1 1 2 2 2 1
2 +1
2023 2
2023 + 2 2023 + + 2 + 2 + ] =
( 1) 2023 2023
0 20232 1 + 1 2 2 2 12 2 2023 + + 2 + 2 + 1,
其除以2023的余数2022和3,
当1 ≤ ≤ 2024且 = 2 1,(1 ≤ ≤ 1011, ∈ )时,
第 11 页,共 12 页
2024 +2024 20242 1+2024 (2 1)
[ ] = [ ( )] = [ (
0
2 12023
2 2 + 1 2 3 2 2
2023 2 1
2023 + + 2 1 + 2 1 +
( 1) 2023
2
)] = ( 02 12023
2 2 + 1 2 32 12023 + +
2 2
2023 2 1
+ 2 ),
其除以2023的余数为2023 (4 1) = 2024 4 ,
当 = 2 1, = 1012时,
2024 +2024 20242 1+2024 (2 1)
[ 0 ] = [ ( )] = [ ( 2 12023
2 2 + 1 2 3 2 2
2023 2 1
2023 + + 2 1 + 2 1 +
( 1) 2023
2
)] = ( 0 20232 2 + 1 2 3 2 2
2023 2 1 2 1
2023 + + 2 1 + 2 + 1),
其除以2023的余数为2021,
除以2023的余数为∑1011( 4 ) + 2022 + 3 + ∑1011 =1 =1 ( 2024 4 ) + 2021除以2023的余数,
即2024 × 1011 + 2022 + 3 + 2021 = 2024 × 1011 + 4046除以2023的余数,
又2024 × 1011 + 4046 = (2023 + 1) × 1011 + 2023 × 2 = 2023 × 1011 + 1011 + 2023 × 2其除以2023的
余数为1011.
第 12 页,共 12 页
同课章节目录
