2023-2024学年上海师大附中高二(下)期中数学试卷(含答案)
文档属性
| 名称 | 2023-2024学年上海师大附中高二(下)期中数学试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 180.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-09 08:15:39 | ||
图片预览




文档简介
2023-2024学年上海师大附中高二(下)期中数学试卷
一、单选题:本题共4小题,共12分。在每小题给出的选项中,只有一项是符合题目要求的。
1.下表是“膜法世家”形象代言人选举得票情况统计,其中周柯宇的票数被污损了无法看清,那么应该当选的人是( )
姓名 张元英 林正英 米卡 周柯宇 林墨 合计
票数
A. 米卡 B. 周柯宇 C. 无法确定 D. 合计
2.高考数学试题中,有道选择题,每道选择题有个选项,其中只有个选项是正确的,则随机选择其中一个选项,正确的概率是,某家长说:“要是都不会做,每题都随机选择其中个选项,则一定有道题答对”这句话( )
A. 正确 B. 错误 C. 不一定 D. 无法解释
3.如图,在下列各正方体中,为正方体的一条体对角线,、分别为所在棱的中点,则满足的是( )
A. B.
C. D.
4.已知,为同一次试验中的两个随机事件,且,,命题甲:若,则事件与相互独立;命题乙:“与相互独立”是“”的充分不必要条件;则命题( )
A. 甲乙都是真命题 B. 甲是真命题,乙是假命题
C. 甲是假命题,乙是真命题 D. 甲乙都是假命题
二、填空题:本题共12小题,共60分。
5.某读书会有名成员,假期他们每个人阅读的本数分别如下:,,,,,则这组数据的分位数为______.
6.一个圆锥的侧面积是其底面积的倍,则该圆锥的母线与底面所成的角为 .
7.已知,则 ______.
8.如图只小猫围绕在的单位正方形的交叉点上,随机选取两只,它们之间距离为的概率是______.
9.在空间直角坐标系中,已知点,,,,若,,,四点共面,则 ______.
10.九章算术中的“商功“篇主要讲述了以立体几何为主的各种形体体积的计算,其中堑堵是指底面为直角三角形的直棱柱.如图,在堑堵中,是的中点,,,,若,则______.
11.二项式定理,又称牛顿二项式定理,由艾萨度克牛顿于年、年间提出,据考证,我国至迟在世纪,北宋数学家贾宪就已经知道了二项式系数法则.在的二项式展开式中,的系数为______.
12.已知空间向量,,则向量在向量上的投影向量的坐标是 .
13.在红楼梦中有一道名为“茄鲞”的佳肴,这道菜用到了鸡脯肉、香菌、新笋、豆腐干、果干、茄子净肉六种原料,烹饪时要求香菌、新笋、豆腐干一起下锅,茄子净肉在鸡脯肉后下锅,最后还需加入精心熬制的鸡汤,则烹饪“茄鲞”时不同的下锅顺序共有______种
14.连接空间几何体上的某两点的直线,如果把该几何体绕此直线旋转角,使该几何体与自身重合,那么称这条直线为该几何体的旋转轴如图,八面体的每一个面都是正三角形,并且个顶点,,,在同一平面内,则这个八面体的旋转轴共有______条
15.设样本空间,,,,,,,的样本点都是等可能出现的,且事件,事件,事件,使得,且满足,,两两不独立,则 ______.
16.已知正四面体的棱长为,动点满足,且,则点的轨迹长为______.
三、解答题:本题共5小题,共78分。解答应写出文字说明,证明过程或演算步骤。
17.本小题分
先后抛掷一枚质地均匀的骰子两次,记向上的点数分别为,,将事件“为整数”记为,将事件“为偶数”记为,将事件“为奇数”记为.
试判断事件与事件是否相互独立?并说明理由;
求的值.
18.本小题分
已知甲组数据,,,的茎叶图如图所示,其中数据的整数部分为茎,数据的小数部分仅一位小数为叶,例如第一个数据为.
甲组数据的平均值、方差、中位数;
乙组数据为,,,,且甲、乙两组数据合并后的个数据的平均值,方差,求乙组数据的平均值和方差,写出必要的计算过程和步骤.
19.本小题分
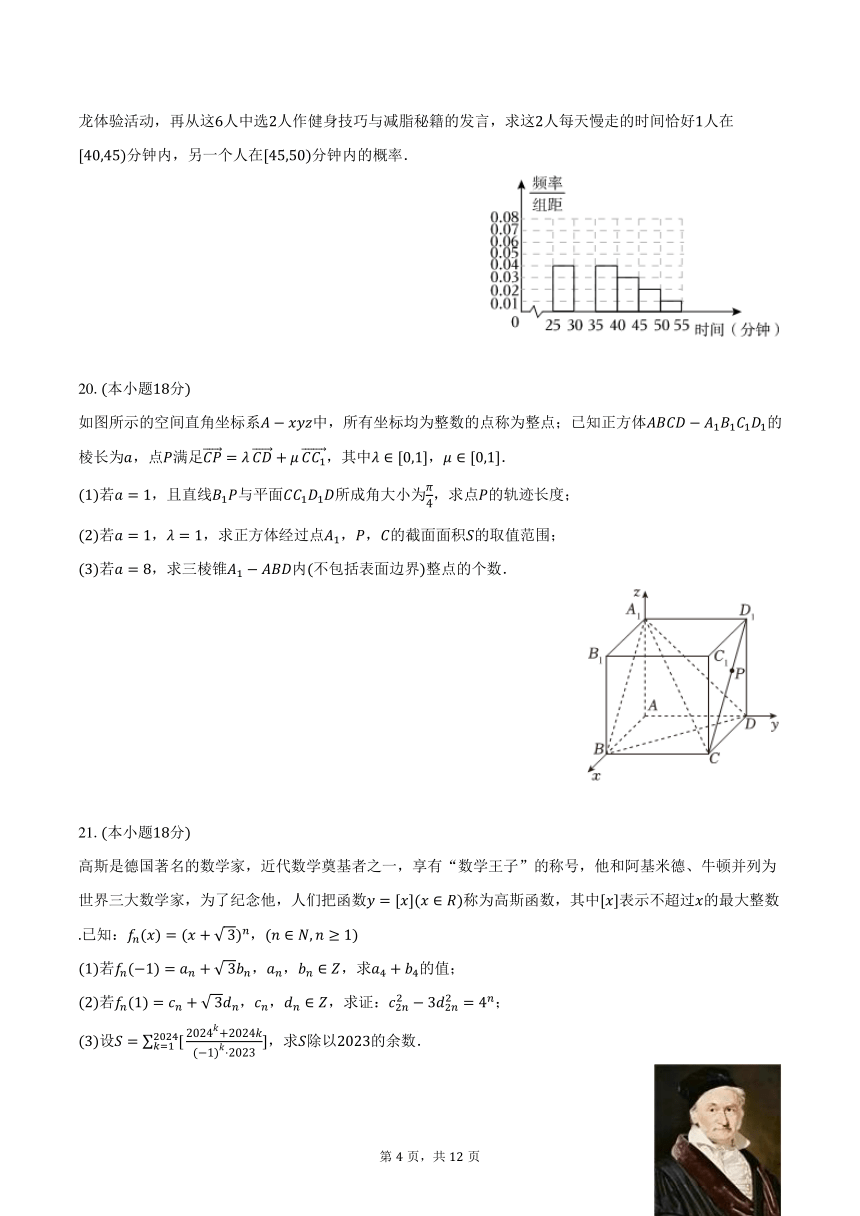
某企业为了了解本企业员工每天慢走与慢跑的情况,对每天慢走时间在分钟到分钟之间的员工,随机抽取人进行调查,将既参加慢走又参加慢跑的人称为“族”,否则称为“非族”,得如下的统计表以及每天慢走时间在分钟到分钟之间的员工人数的频率分布直方图部分:
组数 分组 人数 本组中“族”的比例
试补全频率分布直方图,并求与的值:
从每天慢走时间在分钟内的“族”中按时间采用分层抽样法抽取人参加企业举办的健身沙龙体验活动,再从这人中选人作健身技巧与减脂秘籍的发言,求这人每天慢走的时间恰好人在分钟内,另一个人在分钟内的概率.
20.本小题分
如图所示的空间直角坐标系中,所有坐标均为整数的点称为整点;已知正方体的棱长为,点满足,其中,.
若,且直线与平面所成角大小为,求点的轨迹长度;
若,,求正方体经过点,,的截面面积的取值范围;
若,求三棱锥内不包括表面边界整点的个数.
21.本小题分
高斯是德国著名的数学家,近代数学奠基者之一,享有“数学王子”的称号,他和阿基米德、牛顿并列为世界三大数学家,为了纪念他,人们把函数称为高斯函数,其中表示不超过的最大整数已知:,
若,,,求的值;
若,,,求证:;
设,求除以的余数.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.解:先后两次抛掷一枚质地均匀的骰子,得到向上的点数分别为,,
则基本事件总数为,,,,,,
,,,,,,
,,,,,,
,,,,,,
,,,,,,
,,,,,,共种情况,
满足事件的有,,,,,,,,,,,,,,,,,,,共个,
故,
满足事件的有,,,,,,,,,,,,,,,,,,共个,
故,
满足事件的有,,,,,,,,,共个,
所以,
所以事件与事件相互独立;
满足事件的有,,,,,,,共种,
所以,
所以,
18.解:甲组数据为,,,,,,,,,,,,,,,
所以甲组数据的中位数为,
甲组数据的平均值为.
甲组数据的方差为.
由,可得,
由,解得,,
所以.
19.解:第二组的频率为,
所以第二组小矩形高为补全后的频率直方图如下:
第一组的频率为,所以.
第五组的频率为,所以.
因为分钟的“族”人数为,
分钟的“族”人数为,二者比例为::,
所以按时间采用分层抽样法抽取人,分钟内抽取人,分钟内抽取人.
设这人每天慢走的时间恰好人在分钟,另一个人在分钟为事件,
在分钟内抽取人记为,,,,分钟内抽取人记为,,
则有,,,,,,,,,,,,,,,
共种不同的抽取方法,事件有,,,,,,,,共种,
所以,即选出发言的人每天慢走的时间恰好人在分钟内,
另一个人在分钟内的概率为.
20.解:空间直角坐标系中,所有坐标均为整数的点称为整点,
正方体的棱长为,点满足,其中,,
连接,
平面,为在平面上的射影,
直线与平面所成角的平面角为,
由已知,
则,故点轨迹为以为圆心,为半径的圆在正方形内的部分,
点的轨迹长度为,
在正方体中,以为坐标原点,
以,,所在的直线分别为,,轴建立空间直角坐标系,
,
,,,,
,,
,即,
点在上运动,则,
过点作,交与点,连接,
平面平面,
平面平面,平面平面,
,又,
在正方体中经过点,,的截面为平行四边形,如图,
则,,
点到的距离为:
,
,故当取或时,取到最大值,
此时截面面积的最大值为,
当时,取到最小值,
此时截面面积的最小值为,
当时,在正方体中经过点,,的截面面积的取值范围为.
如图,过轴上的点,,,,,
,,作三棱锥平行于底面的截面,
则三棱锥内不包括表面边界整点一定位于各截面内,
截面内的整点个数为,
截面内的整点个数为,
截面内的整点有个,为,
截面内的整点有个,分别为:,,,
截面内的整点有个,分别为:,,,,,,
截面内的整点有个,分别为:
,,,,,,,
,,,
截面内的整点有个,分别为:
,,,,,,,
,,,,,,,,
三棱锥内不包括表面边界整点个数为.
21.解:因为,,
所以当时,,
而,
因为,,,
所以,,.
因为,,,,
则.
故.
,
又,
则,
又,
所以,
所以当,,
,
其除以的余数为,
当,时,
,
其除以的余数和,
当且,时,
,
其除以的余数为,
当,时,
,
其除以的余数为,
除以的余数为除以的余数,
即除以的余数,
又其除以的余数为.
第1页,共1页
一、单选题:本题共4小题,共12分。在每小题给出的选项中,只有一项是符合题目要求的。
1.下表是“膜法世家”形象代言人选举得票情况统计,其中周柯宇的票数被污损了无法看清,那么应该当选的人是( )
姓名 张元英 林正英 米卡 周柯宇 林墨 合计
票数
A. 米卡 B. 周柯宇 C. 无法确定 D. 合计
2.高考数学试题中,有道选择题,每道选择题有个选项,其中只有个选项是正确的,则随机选择其中一个选项,正确的概率是,某家长说:“要是都不会做,每题都随机选择其中个选项,则一定有道题答对”这句话( )
A. 正确 B. 错误 C. 不一定 D. 无法解释
3.如图,在下列各正方体中,为正方体的一条体对角线,、分别为所在棱的中点,则满足的是( )
A. B.
C. D.
4.已知,为同一次试验中的两个随机事件,且,,命题甲:若,则事件与相互独立;命题乙:“与相互独立”是“”的充分不必要条件;则命题( )
A. 甲乙都是真命题 B. 甲是真命题,乙是假命题
C. 甲是假命题,乙是真命题 D. 甲乙都是假命题
二、填空题:本题共12小题,共60分。
5.某读书会有名成员,假期他们每个人阅读的本数分别如下:,,,,,则这组数据的分位数为______.
6.一个圆锥的侧面积是其底面积的倍,则该圆锥的母线与底面所成的角为 .
7.已知,则 ______.
8.如图只小猫围绕在的单位正方形的交叉点上,随机选取两只,它们之间距离为的概率是______.
9.在空间直角坐标系中,已知点,,,,若,,,四点共面,则 ______.
10.九章算术中的“商功“篇主要讲述了以立体几何为主的各种形体体积的计算,其中堑堵是指底面为直角三角形的直棱柱.如图,在堑堵中,是的中点,,,,若,则______.
11.二项式定理,又称牛顿二项式定理,由艾萨度克牛顿于年、年间提出,据考证,我国至迟在世纪,北宋数学家贾宪就已经知道了二项式系数法则.在的二项式展开式中,的系数为______.
12.已知空间向量,,则向量在向量上的投影向量的坐标是 .
13.在红楼梦中有一道名为“茄鲞”的佳肴,这道菜用到了鸡脯肉、香菌、新笋、豆腐干、果干、茄子净肉六种原料,烹饪时要求香菌、新笋、豆腐干一起下锅,茄子净肉在鸡脯肉后下锅,最后还需加入精心熬制的鸡汤,则烹饪“茄鲞”时不同的下锅顺序共有______种
14.连接空间几何体上的某两点的直线,如果把该几何体绕此直线旋转角,使该几何体与自身重合,那么称这条直线为该几何体的旋转轴如图,八面体的每一个面都是正三角形,并且个顶点,,,在同一平面内,则这个八面体的旋转轴共有______条
15.设样本空间,,,,,,,的样本点都是等可能出现的,且事件,事件,事件,使得,且满足,,两两不独立,则 ______.
16.已知正四面体的棱长为,动点满足,且,则点的轨迹长为______.
三、解答题:本题共5小题,共78分。解答应写出文字说明,证明过程或演算步骤。
17.本小题分
先后抛掷一枚质地均匀的骰子两次,记向上的点数分别为,,将事件“为整数”记为,将事件“为偶数”记为,将事件“为奇数”记为.
试判断事件与事件是否相互独立?并说明理由;
求的值.
18.本小题分
已知甲组数据,,,的茎叶图如图所示,其中数据的整数部分为茎,数据的小数部分仅一位小数为叶,例如第一个数据为.
甲组数据的平均值、方差、中位数;
乙组数据为,,,,且甲、乙两组数据合并后的个数据的平均值,方差,求乙组数据的平均值和方差,写出必要的计算过程和步骤.
19.本小题分
某企业为了了解本企业员工每天慢走与慢跑的情况,对每天慢走时间在分钟到分钟之间的员工,随机抽取人进行调查,将既参加慢走又参加慢跑的人称为“族”,否则称为“非族”,得如下的统计表以及每天慢走时间在分钟到分钟之间的员工人数的频率分布直方图部分:
组数 分组 人数 本组中“族”的比例
试补全频率分布直方图,并求与的值:
从每天慢走时间在分钟内的“族”中按时间采用分层抽样法抽取人参加企业举办的健身沙龙体验活动,再从这人中选人作健身技巧与减脂秘籍的发言,求这人每天慢走的时间恰好人在分钟内,另一个人在分钟内的概率.
20.本小题分
如图所示的空间直角坐标系中,所有坐标均为整数的点称为整点;已知正方体的棱长为,点满足,其中,.
若,且直线与平面所成角大小为,求点的轨迹长度;
若,,求正方体经过点,,的截面面积的取值范围;
若,求三棱锥内不包括表面边界整点的个数.
21.本小题分
高斯是德国著名的数学家,近代数学奠基者之一,享有“数学王子”的称号,他和阿基米德、牛顿并列为世界三大数学家,为了纪念他,人们把函数称为高斯函数,其中表示不超过的最大整数已知:,
若,,,求的值;
若,,,求证:;
设,求除以的余数.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.解:先后两次抛掷一枚质地均匀的骰子,得到向上的点数分别为,,
则基本事件总数为,,,,,,
,,,,,,
,,,,,,
,,,,,,
,,,,,,
,,,,,,共种情况,
满足事件的有,,,,,,,,,,,,,,,,,,,共个,
故,
满足事件的有,,,,,,,,,,,,,,,,,,共个,
故,
满足事件的有,,,,,,,,,共个,
所以,
所以事件与事件相互独立;
满足事件的有,,,,,,,共种,
所以,
所以,
18.解:甲组数据为,,,,,,,,,,,,,,,
所以甲组数据的中位数为,
甲组数据的平均值为.
甲组数据的方差为.
由,可得,
由,解得,,
所以.
19.解:第二组的频率为,
所以第二组小矩形高为补全后的频率直方图如下:
第一组的频率为,所以.
第五组的频率为,所以.
因为分钟的“族”人数为,
分钟的“族”人数为,二者比例为::,
所以按时间采用分层抽样法抽取人,分钟内抽取人,分钟内抽取人.
设这人每天慢走的时间恰好人在分钟,另一个人在分钟为事件,
在分钟内抽取人记为,,,,分钟内抽取人记为,,
则有,,,,,,,,,,,,,,,
共种不同的抽取方法,事件有,,,,,,,,共种,
所以,即选出发言的人每天慢走的时间恰好人在分钟内,
另一个人在分钟内的概率为.
20.解:空间直角坐标系中,所有坐标均为整数的点称为整点,
正方体的棱长为,点满足,其中,,
连接,
平面,为在平面上的射影,
直线与平面所成角的平面角为,
由已知,
则,故点轨迹为以为圆心,为半径的圆在正方形内的部分,
点的轨迹长度为,
在正方体中,以为坐标原点,
以,,所在的直线分别为,,轴建立空间直角坐标系,
,
,,,,
,,
,即,
点在上运动,则,
过点作,交与点,连接,
平面平面,
平面平面,平面平面,
,又,
在正方体中经过点,,的截面为平行四边形,如图,
则,,
点到的距离为:
,
,故当取或时,取到最大值,
此时截面面积的最大值为,
当时,取到最小值,
此时截面面积的最小值为,
当时,在正方体中经过点,,的截面面积的取值范围为.
如图,过轴上的点,,,,,
,,作三棱锥平行于底面的截面,
则三棱锥内不包括表面边界整点一定位于各截面内,
截面内的整点个数为,
截面内的整点个数为,
截面内的整点有个,为,
截面内的整点有个,分别为:,,,
截面内的整点有个,分别为:,,,,,,
截面内的整点有个,分别为:
,,,,,,,
,,,
截面内的整点有个,分别为:
,,,,,,,
,,,,,,,,
三棱锥内不包括表面边界整点个数为.
21.解:因为,,
所以当时,,
而,
因为,,,
所以,,.
因为,,,,
则.
故.
,
又,
则,
又,
所以,
所以当,,
,
其除以的余数为,
当,时,
,
其除以的余数和,
当且,时,
,
其除以的余数为,
当,时,
,
其除以的余数为,
除以的余数为除以的余数,
即除以的余数,
又其除以的余数为.
第1页,共1页
同课章节目录
