广东省佛山市三水区实验中学高中数学新课标人教A版选修2-1课件:1.2充分条件与必要条件(共27张PPT)
文档属性
| 名称 | 广东省佛山市三水区实验中学高中数学新课标人教A版选修2-1课件:1.2充分条件与必要条件(共27张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 306.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-04-16 22:03:59 | ||
图片预览






文档简介
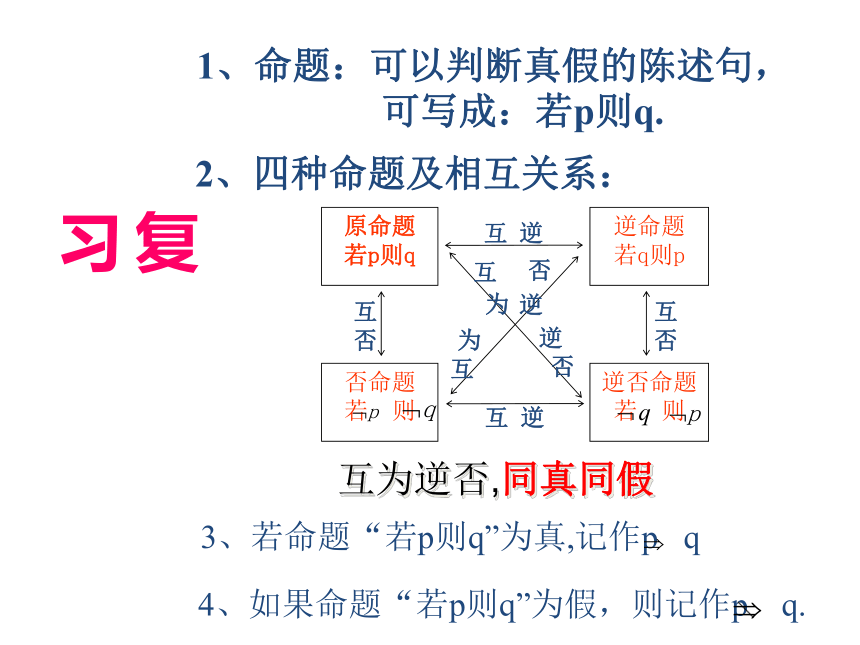
课件27张PPT。充分条件与必要条件 4、如果命题“若p则q”为假,则记作p q.3、若命题“若p则q”为真,记作p q2、四种命题及相互关系:1、命题:可以判断真假的陈述句,
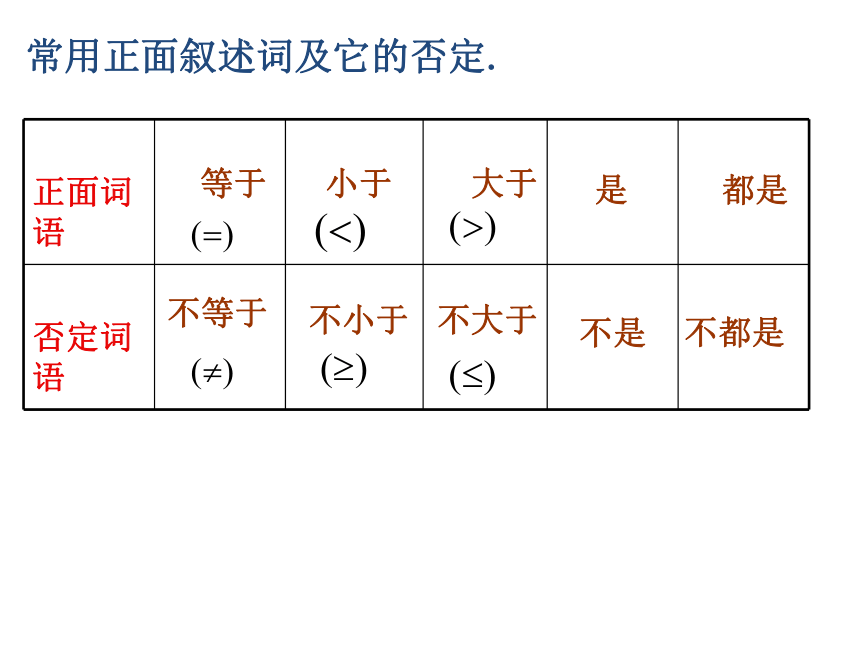
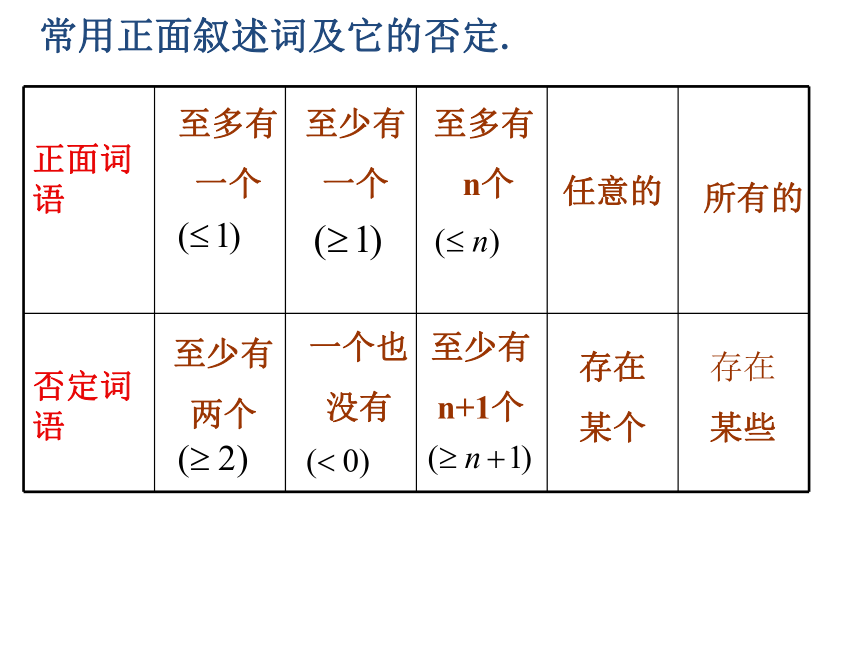
可写成:若p则q. 复习互为逆否,同真同假常用正面叙述词及它的否定. ?等于不等于小于不小于大于不大于是不是都是不都是至多有
一个至少有
两个
至少有
一个一个也
没有至多有
n个至少有
n+1个任意的存在
某个所有的存在
某些常用正面叙述词及它的否定. ?(1)若 ,则 ;
(2)若 ,则 ;
(3)全等三角形的面积相等;
(4)对角线互相垂直的四边形是菱形;
真真假假判断下列命题是真命题还是假命题: 新授课 1、充分条件与必要条件:一般地,用 、 分别表示两个命题,如果命题 成立,可以推出命题 也成立,即 ,那么 叫做 的充分条件, 叫做 的必要条件. 则称:是 的充分条件, 是 的必要条件。P足以导致q,也就是说条件p充分了;
q是p成立所 必须具备的前提两三角形全等 两三角形面积相等两三角形全等是两三角形面积相等的充分条件.两三角形面积相等是两三角形全等的必要条件.练习:课本10页练:1.请用“充分不必要”、“必要不充分”、
“充要”、“既不充分也不必要”填空:
(1)“(x-2)(x-3)=0”是“x=2”的______条件.
(2)“同位角相等”是“两直线平行”的___条件.
(3)“x=3”是“x2=9”的______条件.
(4)“四边形的对角线相等”是“四边形为平行四边形”的__________条件.必要不充分充要充分不必要既不充分也不必要 例1 .指出下列各组命题中,p是q的什么条件,q是p的什么
条件. 例2、以“充分不必要条件”、“必要不充分条件”、“充
要条件”与”既不充分也不必要条件“中选出适当的一种
填空.(充分不必要条件)(充分不必要条件)(必要不充分条件)(必要不充分条件)(充要条件)(充要条件)(既不充分也不必要条件) B A D B例7、若p是r的充分不必要条件,r是q的必要
条件,r又是s的充要条件,q是s的必要条件.
则:
1)s是p的什么条件?
2)r是q的什么条件?必要不充分条件充要条件设集合充分不必要条件2、判断p是q的什么条件?必要不充分条件必要不充分条件必要不充分条件必要不充分条件必要不充分条件充分不必要条件⑴⑵⑶⑷⑸⑹⑺2.充要条件的证明注意:分清p与q.①从命题角度看引申㈠若p则q是真命题,那么p是q的充分条件
q是p的必要条件.㈡若p则q是真命题,若q则p为假命题,那么p是q 的充分不必要条件,q是p必要不充分条件.(四)若p则q,若q则p都是假命题,那么p是q的既不充分也不必要条件,q是p既不充分也不必要条件.(三)若p则q,若q则p都是真命题,那么p是q的充要条件②从集合角度看
命题“若p则q”引申练习:课本12页课堂小结 (3)判别技巧:
① 可先简化命题;
② 否定一个命题只要举出一个反例即可;
③ 将命题转化为等价的逆否命题后再判断。
(1)充分条件、必要条件、充分必要条件的概念. 用反证法证明:圆的两条 不是直径的相交弦不能互相平分.已知:如图,在⊙O中,弦AB、CD交于P,且AB、CD不是直径.求证:弦AB、CD不被P平分.分析:假设弦AB、CD被P平分,连接OP后,可以推出AB、CD都与OP垂直,则出现矛盾.证明: 假设弦AB、CD被P平分,由于P点一定不是圆心O,连接OP,根据垂径定理的推论,有OP⊥AB,OP⊥CD,即过点P有两条直线与OP都垂直,这与垂线性质矛盾.所以,弦AB、CD不被P平分.
可写成:若p则q. 复习互为逆否,同真同假常用正面叙述词及它的否定. ?等于不等于小于不小于大于不大于是不是都是不都是至多有
一个至少有
两个
至少有
一个一个也
没有至多有
n个至少有
n+1个任意的存在
某个所有的存在
某些常用正面叙述词及它的否定. ?(1)若 ,则 ;
(2)若 ,则 ;
(3)全等三角形的面积相等;
(4)对角线互相垂直的四边形是菱形;
真真假假判断下列命题是真命题还是假命题: 新授课 1、充分条件与必要条件:一般地,用 、 分别表示两个命题,如果命题 成立,可以推出命题 也成立,即 ,那么 叫做 的充分条件, 叫做 的必要条件. 则称:是 的充分条件, 是 的必要条件。P足以导致q,也就是说条件p充分了;
q是p成立所 必须具备的前提两三角形全等 两三角形面积相等两三角形全等是两三角形面积相等的充分条件.两三角形面积相等是两三角形全等的必要条件.练习:课本10页练:1.请用“充分不必要”、“必要不充分”、
“充要”、“既不充分也不必要”填空:
(1)“(x-2)(x-3)=0”是“x=2”的______条件.
(2)“同位角相等”是“两直线平行”的___条件.
(3)“x=3”是“x2=9”的______条件.
(4)“四边形的对角线相等”是“四边形为平行四边形”的__________条件.必要不充分充要充分不必要既不充分也不必要 例1 .指出下列各组命题中,p是q的什么条件,q是p的什么
条件. 例2、以“充分不必要条件”、“必要不充分条件”、“充
要条件”与”既不充分也不必要条件“中选出适当的一种
填空.(充分不必要条件)(充分不必要条件)(必要不充分条件)(必要不充分条件)(充要条件)(充要条件)(既不充分也不必要条件) B A D B例7、若p是r的充分不必要条件,r是q的必要
条件,r又是s的充要条件,q是s的必要条件.
则:
1)s是p的什么条件?
2)r是q的什么条件?必要不充分条件充要条件设集合充分不必要条件2、判断p是q的什么条件?必要不充分条件必要不充分条件必要不充分条件必要不充分条件必要不充分条件充分不必要条件⑴⑵⑶⑷⑸⑹⑺2.充要条件的证明注意:分清p与q.①从命题角度看引申㈠若p则q是真命题,那么p是q的充分条件
q是p的必要条件.㈡若p则q是真命题,若q则p为假命题,那么p是q 的充分不必要条件,q是p必要不充分条件.(四)若p则q,若q则p都是假命题,那么p是q的既不充分也不必要条件,q是p既不充分也不必要条件.(三)若p则q,若q则p都是真命题,那么p是q的充要条件②从集合角度看
命题“若p则q”引申练习:课本12页课堂小结 (3)判别技巧:
① 可先简化命题;
② 否定一个命题只要举出一个反例即可;
③ 将命题转化为等价的逆否命题后再判断。
(1)充分条件、必要条件、充分必要条件的概念. 用反证法证明:圆的两条 不是直径的相交弦不能互相平分.已知:如图,在⊙O中,弦AB、CD交于P,且AB、CD不是直径.求证:弦AB、CD不被P平分.分析:假设弦AB、CD被P平分,连接OP后,可以推出AB、CD都与OP垂直,则出现矛盾.证明: 假设弦AB、CD被P平分,由于P点一定不是圆心O,连接OP,根据垂径定理的推论,有OP⊥AB,OP⊥CD,即过点P有两条直线与OP都垂直,这与垂线性质矛盾.所以,弦AB、CD不被P平分.
