新人教版七年数学上册第一章 《有理数》数的分类专项训练(含部分解析)
文档属性
| 名称 | 新人教版七年数学上册第一章 《有理数》数的分类专项训练(含部分解析) |  | |
| 格式 | docx | ||
| 文件大小 | 593.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-10 14:54:23 | ||
图片预览



文档简介
新人教版七年数学上册《有理数》数的分类专项训练
姓名: 学校: 班级:
【知识归纳】
实数:有理数和无理数。(平时见到的几乎都是实数)
有理数:整数和分数。 或者正有理、0、负有理数。
无理数:无限不循环小数、化简后含根号的数。
整数:负整数、0、正整数; 其中0、正整数并称自然数。
分数:正分数、负分数。(小数也属于分数)
负数(小于0的数):负有理、负无理数。
(一般看数字前面的符号化简后为+,如:-(-2)和π是正数,也是无理数)
正数(大于0的数):正有理、正无理数。
(一般看数字前面的符号化简后为-,如:-[(-2)]和-π是正数,也是无理数)
非负数(不要负数):0和正数。
非正数(不要正数):0和负数。
非负整数:正整数和零。(不是负的整数)
非正整数:负整数及0。
【配套训练】
一、直接分类
1.把下面个各数填入相应的大括号内
,5,0,,3.14,+27,,,.
整数集合:{__________________________________________...}
非负整数集合:{____________________________________...}
负分数集合:{__________________________________________...}
正有理数集合:{__________________________________________...}.
2.把下面各数填在相应的大括号内:
1;;;
(1)非负整数集合{___________________________________}
(2)负分数集合{___________________________________}
(3)正有理数集合{___________________________________}
3.将下面各数填入它们属于的集合内:
,,,,,,,,
正有理数集合:{____________________________________…};
负有理数集合:{____________________________________…};
整数集合:{__________________________________________…}.
4.将下列各数按照分类填入下面对应的大括号内
.
有理数集合:{ …} 整数集合:{ …}
负数集合:{ …} 分数集合:{ …}
5.把下面各数填在相应的大括号里(将各数用逗号分开):
,3.141,0,2012,,,,,.
负整数集:{ …}; 正分数集:{ …};
自然数集:{ …};有理数集:{ …}.
6.把下面各数填在相应的大括号里(将各数用逗号分开):,,,, ,,,,.
负整数集合{ ……} 整数集合{ ……}
正分数集合{ ……}
非负整数集合{ ……} 有理数{ ……}
7.把下面各数填在相应的大括号里(将各数用逗号分开):
,,0,,,,,.
负整数集合{___ ____}
正数集合{____ ___}
正分数集合{___ ____}
非负整数集合{___ ____}
二、重叠分类。
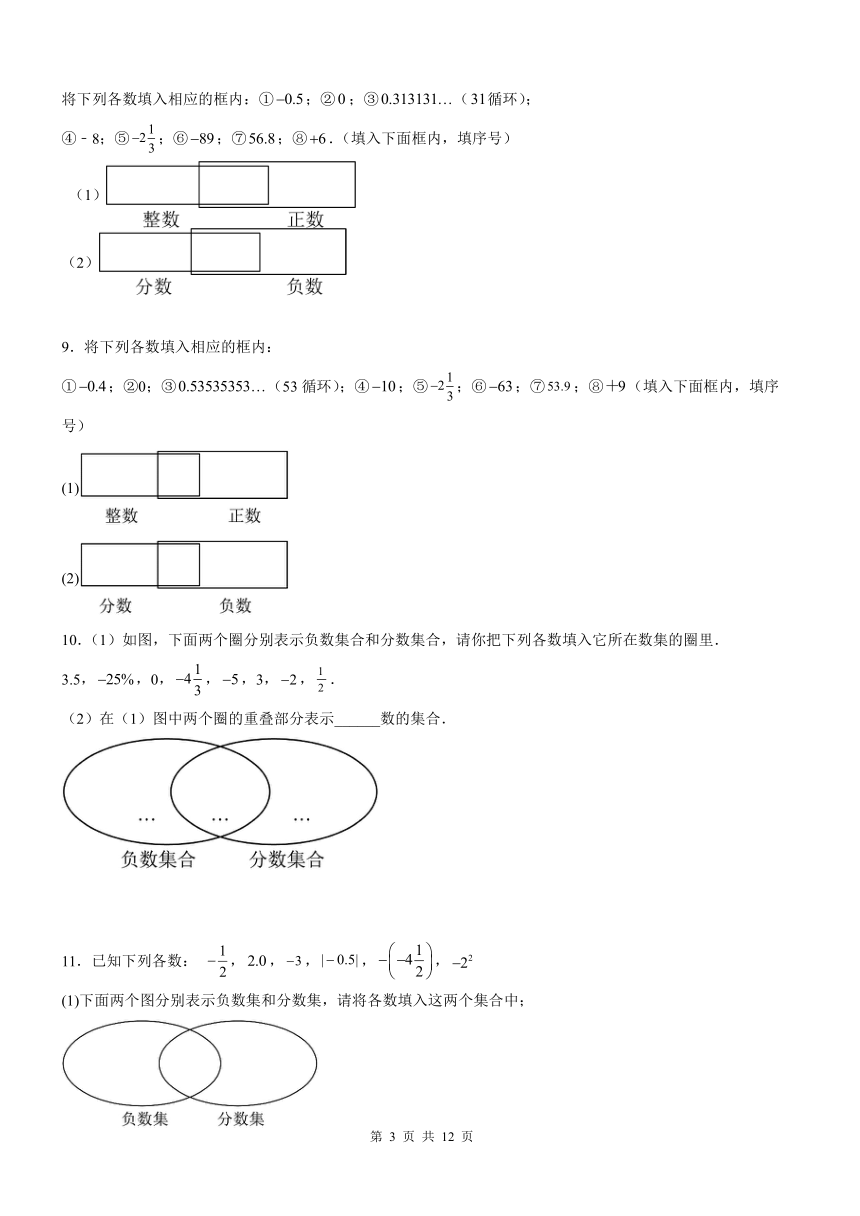
将下列各数填入相应的框内:①;②;③(循环);
④﹣8;⑤;⑥;⑦;⑧.(填入下面框内,填序号)
(1)
(2)
9.将下列各数填入相应的框内:
①;②0;③(53循环);④;⑤;⑥;⑦;⑧(填入下面框内,填序号)
(1)
(2)
10.(1)如图,下面两个圈分别表示负数集合和分数集合,请你把下列各数填入它所在数集的圈里.
3.5,,0,,,3,,.
(2)在(1)图中两个圈的重叠部分表示______数的集合.
11.已知下列各数: ,,,,,
(1)下面两个图分别表示负数集和分数集,请将各数填入这两个集合中;
(2)画出数轴,把它们分别在数轴上表示出来,并用连接起来.
12.(1)如图,下面两个图分别表示负数集合和分数集合,请你把下列各数填入它所在数集的圈里.
3.5,,0,,,3,,.
(2)在(1)图中两个圈的重叠部分表示____________数的集合.
(3)列式并计算:在(1)的数据中,求最大的数与最小的数的和.
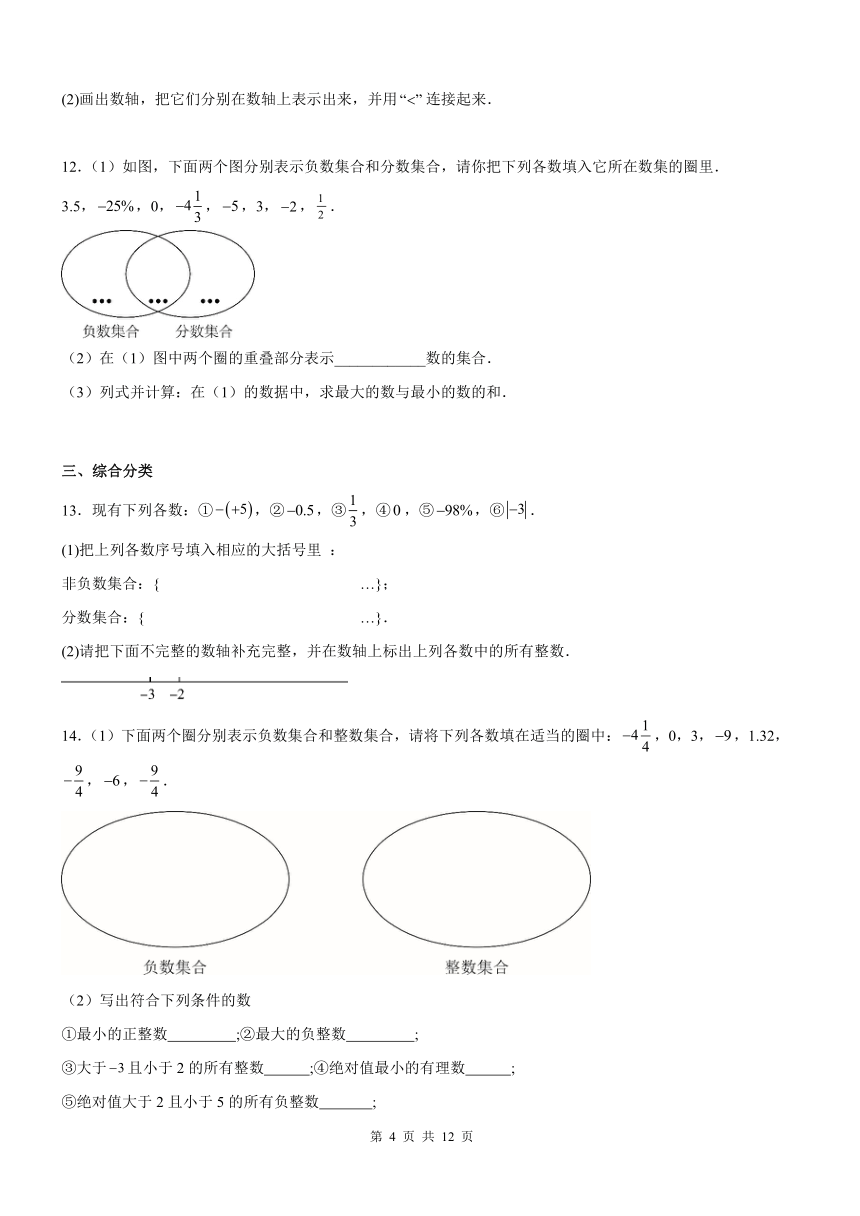
三、综合分类
13.现有下列各数:①,②,③,④,⑤,⑥.
(1)把上列各数序号填入相应的大括号里 :
非负数集合:{ …};
分数集合:{ …}.
(2)请把下面不完整的数轴补充完整,并在数轴上标出上列各数中的所有整数.
14.(1)下面两个圈分别表示负数集合和整数集合,请将下列各数填在适当的圈中:,0,3,,1.32,,,.
(2)写出符合下列条件的数
①最小的正整数 ;②最大的负整数 ;
③大于且小于2的所有整数 ;④绝对值最小的有理数 ;
⑤绝对值大于2且小于5的所有负整数 ;
⑥在数轴上,与表示的点的距离为2的所有的数 .
(3)计算填空
, , ,
, , .
15.(1)下面两个圈分别表示负数集合和整数集合,请将下列各数填在适当的圈中:,0,3,,1.32,,.
(2)写出符合下列条件的数
①最小的正整数 ;②最大的负整数 ;③大于且小于2的所有整数 ;
④绝对值最小的有理数 ;⑤绝对值大于2且小于5的所有负整数 ;
⑥在数轴上,与表示的点的距离为2的所有数 .
参考答案:
1.5,0,,+27,
5,0,+27,
,,
5,3.14,+27,
【分析】整数包括正整数、零、负整数,非负数有正整数和零,负分数有小于零的分数,正有理数包括正整数和正分数.
【详解】可以化成分数,即为负分数;5为正整数;0是零,负整数;3.14正分数;+27为正整数;为负分数;为负分数;可以化为正整数7,即为正整数.
整数集合:5,0,,+27,;
非负整数集合:5,0,+27,;
负分数集合:,,;
正有理数集合:5,3.14,+27,;
【点睛】本题主要考查有理数、整数、非负数、负数的概念,准确理解各自概念是解题的关键.
2.(1)1;
(2);
(3)1; ;
【分析】(1)根据有理数的分类,即可求解;
(2)根据有理数的分类,即可求解;
(3)根据有理数的分类,即可求解.
【详解】(1)解:;;
非负整数集合{1;}
故答案为:1;
(2)解:负分数集合{;}
故答案为:;
(3)解:正有理数集合{1; ;}
故答案为:1; ;
【点睛】本题主要考查了有理数的分类,熟练掌握有理数的分类是解题的关键.
3.答案见解析
【分析】本题主要考查了有理数的分类,直接根据有理数的分类方法求解即可.
【详解】解:正有理数集合:{,,,,,…};
负有理数集合:{,,,…};
整数集合:{,,,…}.
4.见解析
【分析】本题考查了有理数的分类,根据整数和分数统称为有理数进行分类即可,熟练掌握知识点是解题的关键.
【详解】解:有理数集合:{…}
整数集合:{…}
负数集合:{…}
分数集合:{…}
5.见解析
【分析】本题考查了有理数的分类,根据负整数、正分数、自然数、有理数的概念即可得出答案,熟练掌握相关定义是解此题的关键.
【详解】解:负整数集:{,};
正分数集:{3.141,,};
自然数集:{0,2012,};
有理数集:{,3.141,0,2012,,,,}.
6.见解析
【分析】本题考查了正数,负数,整数,分数,有理数,以及无理数的概念,解题的关键是熟练掌握相关定义,要注意的是本题中的是无限不循环小数,为无理数.
【详解】解: ,,,,
这些数可按如下分类,
负整数集合{,……}整数集合{,,,,……}
正分数集合{,……}非负整数集合{,,……}
有理数{,,,,,,,……}
7.见解析
【分析】本题考查了正数,负数,整数,分数,有理数,以及无理数的概念.要注意的是本题中的是无限不循环小数,为无理数.
【详解】解:,,
这些数可按如下分类,
负整数集合{,…}正数集合{,,,…}
正分数集合{,…}非负整数集合{,…}.
8.见解析
【分析】根据有理数的分类填写即可求解.
【详解】解:(1)整数有②;④;⑥,⑧.正整数有⑧,正数有③(循环);⑦;⑧.
(2)分数有①;③(循环);⑤;⑦;负的分数有①;负数有①;④;⑤;⑥;
(1) (2)
【点睛】本题考查了有理数的分类,熟练掌握有理数的分类是解题的关键.
9.(1)整数:②④⑥⑧;重叠部分:⑧;正数:③⑦⑧;
(2)分数:①③⑤⑦;重叠部分:①⑤;负数:①④⑤⑥.
【分析】(1)根据整数、正数的定义进行解答即可;
(2)根据有限小数和无限循环小数可化为分数和负数的定义进行解答即可.
【详解】(1)解:②0;④;⑥;⑧为整数,
整数为:②④⑥⑧,
③(53循环);⑦;⑧为正数,
正数为:③⑦⑧,
重叠部分为:⑧;
(2)解:①;③(53循环);⑤;⑦为分数 ,
分数为:①③⑤⑦,
①;④;⑤;⑥为负数,
负数为:①④⑤⑥,
重叠部分为:①⑤.
【点睛】本题考查正数和负数,利用有理数的分类是本题的关键.
10.(1)见解析;(2)负分数
【分析】(1)根据负数和分数的概念即可得出答案;
(2)根据负数和分数的概念即可得出答案.
【详解】(1)负数为:,,,;
分数为:3.5,,,;
既是负数又是分数的为:,;
(2)在(1)图中两个圈的重叠部分表示负分数.
【点睛】本题考查了分数和负数的概念,熟练掌握有理数的分类是解题的关键.
11.(1)见解析
(2),见解析
【分析】(1)根据有理数的分类先填中间的负分数,再添左右两边即可;
(2)先化简能够化简的数,再在数轴上描出各数,利用数轴右边的数大于左边的数可得答案.
【详解】(1)解:, ,,
∴把各数填入如下图:
(2), ,,
在数轴上表示为:
∴ .
【点睛】本题考查的是有理数的分类,在数轴上表示有理数,有理数的大小比较,绝对值的含义,有理数的乘方运算,掌握以上基础知识是解本题的关键.
12.(1)见解析(2)负分(3)
【分析】(1)根据负数和分数的定义分类即可;
(2)两个圈重叠的部分表示负分数集合;
(3)最大的数为3.5,最小的数为,计算即可.
【详解】(1)解:根据题意可得:
(2)这两个圈的重叠部分表示负分数集合;
故答案为:负分;
(3)在(1)的数据中,最大的数为3.5,最小的数为,
.
【点睛】本题考查有理数的运算和有理数的分类;熟练掌握有理数的分类,并能准确对有理数的加减法进行运算是解题的关键.
13.(1)③④⑥;②③⑤
(2)见解析
【分析】本题考查了有理数的分类,画数轴并在数轴上表示有理数;
(1)根据有理数的分类方法解答即可;
(2)补充数轴,然后标出所有的整数,即可求解.
【详解】(1)解:①,②,③,④,⑤,⑥
非负数集合:{③④⑥…};
分数集合:{②③⑤…}
故答案为:③④⑥;②③⑤.
(2)解:如图所示,
14.(1)负数集合:,,,,;整数集合:0,3,,;
(2)①1;②;③,,0,1;④0;⑤,;⑥1,;
(3);;;;;
【分析】(1)比0小的数叫负数,正整数、零、负整数的集合是整数,根据定义判断即可得出答案;
(2)根据正整数、负整数的含义、绝对值的性质、数轴上两点的距离公式,逐一分析即可得出答案;
(3)根据有理数混合运算的法则分别计算,即可得出答案.
【详解】解:(1)根据负数和整数的含义分类可得:
负数集合:,,,,;
整数集合:0,3,,;
故答案为:,,,,;0,3,,;
(2)①最小的正整数是1;
②最大的负整数是;
③大于且小于2的所有整数有,,0,1;
④绝对值最小的有理数是0;
⑤绝对值大于2且小于5的所有负整数,;
⑥设在数轴上,与表示的点的距离为2的数为,
则有:
解得:
在数轴上,与表示的点的距离为2的所有数为1,;
故答案为:①1;②;③,,0,1;④0;⑤,;⑥1,;
(3);
;
;
;
;
,
故答案为:;;;;;.
【点睛】此题考查正整数、负整数、正负数的含义,绝对值的性质,数轴上两点距离公式,有理数混合运算方法,掌握相关概念和方法是解题关键.
15.(1),,,;0,3,,;(2)①1;②;③,,0,1;④0;⑤,;⑥1,;(3);;;;;
【分析】本题考查了有理数的分类,绝对值的理解,有理数加、减、乘、除、乘方运算;
(1)按有理数分类方法进行分类,即可求解;
(2)按整数的分类、绝对值的理解、数轴上两点之间的距离,逐一填空,即可求解;
(3)按有理数加、减、乘、除、乘方进行逐一运算,即可求解;
理解有理数的分类方法,绝对值,掌握有理数加、减、乘、除、乘方运算法则是解题的关键.
【详解】解:(1)根据负数和整数的含义分类可得:
负数集合:,,,;
整数集合:0,3,,;
故答案为:,,,;0,3,,;
(2)①最小的正整数是1;
②最大的负整数是;
③大于且小于2的所有整数有,,0,1;
④绝对值最小的有理数是0;
⑤绝对值大于2且小于5的所有负整数,;
⑥设在数轴上,与表示的点的距离为2的数为,
则有:
解得:,,
在数轴上,与表示的点的距离为2的所有数为1,;
故答案为:①1;②;③,,0,1;④0;⑤,;⑥1,;
姓名: 学校: 班级:
【知识归纳】
实数:有理数和无理数。(平时见到的几乎都是实数)
有理数:整数和分数。 或者正有理、0、负有理数。
无理数:无限不循环小数、化简后含根号的数。
整数:负整数、0、正整数; 其中0、正整数并称自然数。
分数:正分数、负分数。(小数也属于分数)
负数(小于0的数):负有理、负无理数。
(一般看数字前面的符号化简后为+,如:-(-2)和π是正数,也是无理数)
正数(大于0的数):正有理、正无理数。
(一般看数字前面的符号化简后为-,如:-[(-2)]和-π是正数,也是无理数)
非负数(不要负数):0和正数。
非正数(不要正数):0和负数。
非负整数:正整数和零。(不是负的整数)
非正整数:负整数及0。
【配套训练】
一、直接分类
1.把下面个各数填入相应的大括号内
,5,0,,3.14,+27,,,.
整数集合:{__________________________________________...}
非负整数集合:{____________________________________...}
负分数集合:{__________________________________________...}
正有理数集合:{__________________________________________...}.
2.把下面各数填在相应的大括号内:
1;;;
(1)非负整数集合{___________________________________}
(2)负分数集合{___________________________________}
(3)正有理数集合{___________________________________}
3.将下面各数填入它们属于的集合内:
,,,,,,,,
正有理数集合:{____________________________________…};
负有理数集合:{____________________________________…};
整数集合:{__________________________________________…}.
4.将下列各数按照分类填入下面对应的大括号内
.
有理数集合:{ …} 整数集合:{ …}
负数集合:{ …} 分数集合:{ …}
5.把下面各数填在相应的大括号里(将各数用逗号分开):
,3.141,0,2012,,,,,.
负整数集:{ …}; 正分数集:{ …};
自然数集:{ …};有理数集:{ …}.
6.把下面各数填在相应的大括号里(将各数用逗号分开):,,,, ,,,,.
负整数集合{ ……} 整数集合{ ……}
正分数集合{ ……}
非负整数集合{ ……} 有理数{ ……}
7.把下面各数填在相应的大括号里(将各数用逗号分开):
,,0,,,,,.
负整数集合{___ ____}
正数集合{____ ___}
正分数集合{___ ____}
非负整数集合{___ ____}
二、重叠分类。
将下列各数填入相应的框内:①;②;③(循环);
④﹣8;⑤;⑥;⑦;⑧.(填入下面框内,填序号)
(1)
(2)
9.将下列各数填入相应的框内:
①;②0;③(53循环);④;⑤;⑥;⑦;⑧(填入下面框内,填序号)
(1)
(2)
10.(1)如图,下面两个圈分别表示负数集合和分数集合,请你把下列各数填入它所在数集的圈里.
3.5,,0,,,3,,.
(2)在(1)图中两个圈的重叠部分表示______数的集合.
11.已知下列各数: ,,,,,
(1)下面两个图分别表示负数集和分数集,请将各数填入这两个集合中;
(2)画出数轴,把它们分别在数轴上表示出来,并用连接起来.
12.(1)如图,下面两个图分别表示负数集合和分数集合,请你把下列各数填入它所在数集的圈里.
3.5,,0,,,3,,.
(2)在(1)图中两个圈的重叠部分表示____________数的集合.
(3)列式并计算:在(1)的数据中,求最大的数与最小的数的和.
三、综合分类
13.现有下列各数:①,②,③,④,⑤,⑥.
(1)把上列各数序号填入相应的大括号里 :
非负数集合:{ …};
分数集合:{ …}.
(2)请把下面不完整的数轴补充完整,并在数轴上标出上列各数中的所有整数.
14.(1)下面两个圈分别表示负数集合和整数集合,请将下列各数填在适当的圈中:,0,3,,1.32,,,.
(2)写出符合下列条件的数
①最小的正整数 ;②最大的负整数 ;
③大于且小于2的所有整数 ;④绝对值最小的有理数 ;
⑤绝对值大于2且小于5的所有负整数 ;
⑥在数轴上,与表示的点的距离为2的所有的数 .
(3)计算填空
, , ,
, , .
15.(1)下面两个圈分别表示负数集合和整数集合,请将下列各数填在适当的圈中:,0,3,,1.32,,.
(2)写出符合下列条件的数
①最小的正整数 ;②最大的负整数 ;③大于且小于2的所有整数 ;
④绝对值最小的有理数 ;⑤绝对值大于2且小于5的所有负整数 ;
⑥在数轴上,与表示的点的距离为2的所有数 .
参考答案:
1.5,0,,+27,
5,0,+27,
,,
5,3.14,+27,
【分析】整数包括正整数、零、负整数,非负数有正整数和零,负分数有小于零的分数,正有理数包括正整数和正分数.
【详解】可以化成分数,即为负分数;5为正整数;0是零,负整数;3.14正分数;+27为正整数;为负分数;为负分数;可以化为正整数7,即为正整数.
整数集合:5,0,,+27,;
非负整数集合:5,0,+27,;
负分数集合:,,;
正有理数集合:5,3.14,+27,;
【点睛】本题主要考查有理数、整数、非负数、负数的概念,准确理解各自概念是解题的关键.
2.(1)1;
(2);
(3)1; ;
【分析】(1)根据有理数的分类,即可求解;
(2)根据有理数的分类,即可求解;
(3)根据有理数的分类,即可求解.
【详解】(1)解:;;
非负整数集合{1;}
故答案为:1;
(2)解:负分数集合{;}
故答案为:;
(3)解:正有理数集合{1; ;}
故答案为:1; ;
【点睛】本题主要考查了有理数的分类,熟练掌握有理数的分类是解题的关键.
3.答案见解析
【分析】本题主要考查了有理数的分类,直接根据有理数的分类方法求解即可.
【详解】解:正有理数集合:{,,,,,…};
负有理数集合:{,,,…};
整数集合:{,,,…}.
4.见解析
【分析】本题考查了有理数的分类,根据整数和分数统称为有理数进行分类即可,熟练掌握知识点是解题的关键.
【详解】解:有理数集合:{…}
整数集合:{…}
负数集合:{…}
分数集合:{…}
5.见解析
【分析】本题考查了有理数的分类,根据负整数、正分数、自然数、有理数的概念即可得出答案,熟练掌握相关定义是解此题的关键.
【详解】解:负整数集:{,};
正分数集:{3.141,,};
自然数集:{0,2012,};
有理数集:{,3.141,0,2012,,,,}.
6.见解析
【分析】本题考查了正数,负数,整数,分数,有理数,以及无理数的概念,解题的关键是熟练掌握相关定义,要注意的是本题中的是无限不循环小数,为无理数.
【详解】解: ,,,,
这些数可按如下分类,
负整数集合{,……}整数集合{,,,,……}
正分数集合{,……}非负整数集合{,,……}
有理数{,,,,,,,……}
7.见解析
【分析】本题考查了正数,负数,整数,分数,有理数,以及无理数的概念.要注意的是本题中的是无限不循环小数,为无理数.
【详解】解:,,
这些数可按如下分类,
负整数集合{,…}正数集合{,,,…}
正分数集合{,…}非负整数集合{,…}.
8.见解析
【分析】根据有理数的分类填写即可求解.
【详解】解:(1)整数有②;④;⑥,⑧.正整数有⑧,正数有③(循环);⑦;⑧.
(2)分数有①;③(循环);⑤;⑦;负的分数有①;负数有①;④;⑤;⑥;
(1) (2)
【点睛】本题考查了有理数的分类,熟练掌握有理数的分类是解题的关键.
9.(1)整数:②④⑥⑧;重叠部分:⑧;正数:③⑦⑧;
(2)分数:①③⑤⑦;重叠部分:①⑤;负数:①④⑤⑥.
【分析】(1)根据整数、正数的定义进行解答即可;
(2)根据有限小数和无限循环小数可化为分数和负数的定义进行解答即可.
【详解】(1)解:②0;④;⑥;⑧为整数,
整数为:②④⑥⑧,
③(53循环);⑦;⑧为正数,
正数为:③⑦⑧,
重叠部分为:⑧;
(2)解:①;③(53循环);⑤;⑦为分数 ,
分数为:①③⑤⑦,
①;④;⑤;⑥为负数,
负数为:①④⑤⑥,
重叠部分为:①⑤.
【点睛】本题考查正数和负数,利用有理数的分类是本题的关键.
10.(1)见解析;(2)负分数
【分析】(1)根据负数和分数的概念即可得出答案;
(2)根据负数和分数的概念即可得出答案.
【详解】(1)负数为:,,,;
分数为:3.5,,,;
既是负数又是分数的为:,;
(2)在(1)图中两个圈的重叠部分表示负分数.
【点睛】本题考查了分数和负数的概念,熟练掌握有理数的分类是解题的关键.
11.(1)见解析
(2),见解析
【分析】(1)根据有理数的分类先填中间的负分数,再添左右两边即可;
(2)先化简能够化简的数,再在数轴上描出各数,利用数轴右边的数大于左边的数可得答案.
【详解】(1)解:, ,,
∴把各数填入如下图:
(2), ,,
在数轴上表示为:
∴ .
【点睛】本题考查的是有理数的分类,在数轴上表示有理数,有理数的大小比较,绝对值的含义,有理数的乘方运算,掌握以上基础知识是解本题的关键.
12.(1)见解析(2)负分(3)
【分析】(1)根据负数和分数的定义分类即可;
(2)两个圈重叠的部分表示负分数集合;
(3)最大的数为3.5,最小的数为,计算即可.
【详解】(1)解:根据题意可得:
(2)这两个圈的重叠部分表示负分数集合;
故答案为:负分;
(3)在(1)的数据中,最大的数为3.5,最小的数为,
.
【点睛】本题考查有理数的运算和有理数的分类;熟练掌握有理数的分类,并能准确对有理数的加减法进行运算是解题的关键.
13.(1)③④⑥;②③⑤
(2)见解析
【分析】本题考查了有理数的分类,画数轴并在数轴上表示有理数;
(1)根据有理数的分类方法解答即可;
(2)补充数轴,然后标出所有的整数,即可求解.
【详解】(1)解:①,②,③,④,⑤,⑥
非负数集合:{③④⑥…};
分数集合:{②③⑤…}
故答案为:③④⑥;②③⑤.
(2)解:如图所示,
14.(1)负数集合:,,,,;整数集合:0,3,,;
(2)①1;②;③,,0,1;④0;⑤,;⑥1,;
(3);;;;;
【分析】(1)比0小的数叫负数,正整数、零、负整数的集合是整数,根据定义判断即可得出答案;
(2)根据正整数、负整数的含义、绝对值的性质、数轴上两点的距离公式,逐一分析即可得出答案;
(3)根据有理数混合运算的法则分别计算,即可得出答案.
【详解】解:(1)根据负数和整数的含义分类可得:
负数集合:,,,,;
整数集合:0,3,,;
故答案为:,,,,;0,3,,;
(2)①最小的正整数是1;
②最大的负整数是;
③大于且小于2的所有整数有,,0,1;
④绝对值最小的有理数是0;
⑤绝对值大于2且小于5的所有负整数,;
⑥设在数轴上,与表示的点的距离为2的数为,
则有:
解得:
在数轴上,与表示的点的距离为2的所有数为1,;
故答案为:①1;②;③,,0,1;④0;⑤,;⑥1,;
(3);
;
;
;
;
,
故答案为:;;;;;.
【点睛】此题考查正整数、负整数、正负数的含义,绝对值的性质,数轴上两点距离公式,有理数混合运算方法,掌握相关概念和方法是解题关键.
15.(1),,,;0,3,,;(2)①1;②;③,,0,1;④0;⑤,;⑥1,;(3);;;;;
【分析】本题考查了有理数的分类,绝对值的理解,有理数加、减、乘、除、乘方运算;
(1)按有理数分类方法进行分类,即可求解;
(2)按整数的分类、绝对值的理解、数轴上两点之间的距离,逐一填空,即可求解;
(3)按有理数加、减、乘、除、乘方进行逐一运算,即可求解;
理解有理数的分类方法,绝对值,掌握有理数加、减、乘、除、乘方运算法则是解题的关键.
【详解】解:(1)根据负数和整数的含义分类可得:
负数集合:,,,;
整数集合:0,3,,;
故答案为:,,,;0,3,,;
(2)①最小的正整数是1;
②最大的负整数是;
③大于且小于2的所有整数有,,0,1;
④绝对值最小的有理数是0;
⑤绝对值大于2且小于5的所有负整数,;
⑥设在数轴上,与表示的点的距离为2的数为,
则有:
解得:,,
在数轴上,与表示的点的距离为2的所有数为1,;
故答案为:①1;②;③,,0,1;④0;⑤,;⑥1,;
同课章节目录
