2024-2025学年人教版数学八年级(上)期末综合提高训练卷(含答案)
文档属性
| 名称 | 2024-2025学年人教版数学八年级(上)期末综合提高训练卷(含答案) | 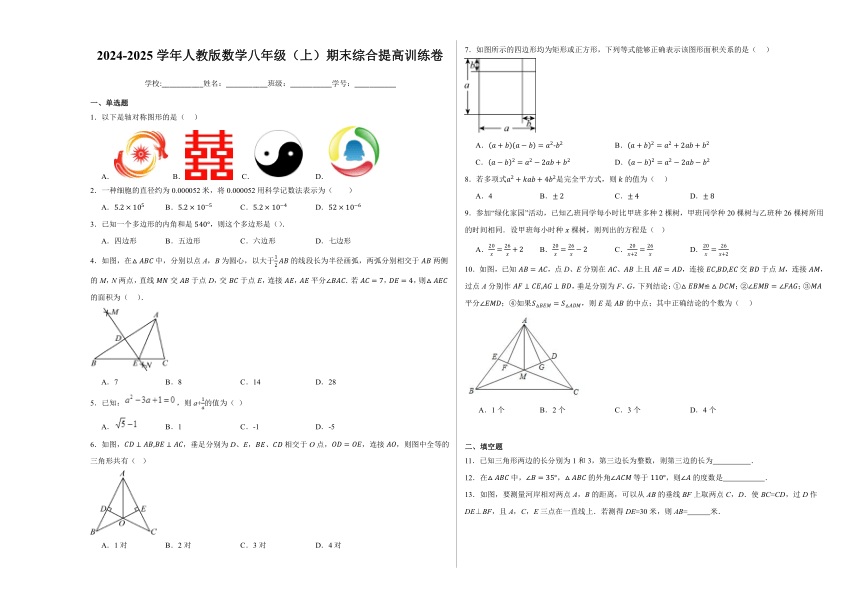 | |
| 格式 | docx | ||
| 文件大小 | 480.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-11 14:29:40 | ||
图片预览



文档简介
2024-2025学年人教版数学八年级(上)期末综合提高训练卷
学校:___________姓名:___________班级:___________学号:___________
一、单选题
1.以下是轴对称图形的是( )
A. B. C. D.
2.一种细胞的直径约为0.000052米,将0.000052用科学记数法表示为( )
A. B. C. D.
3.已知一个多边形的内角和是,则这个多边形是().
A.四边形 B.五边形 C.六边形 D.七边形
4.如图,在中,分别以点A,B为圆心,以大于的线段长为半径画弧,两弧分别相交于两侧的M,N两点,直线交于点D,交于点E,连接,平分.若,,则的面积为( ).
A.7 B.8 C.14 D.28
5.已知:,则a+的值为( )
A. B.1 C.-1 D.-5
6.如图,,垂足分别为D、E,相交于O点,,连接,则图中全等的三角形共有( )
A.1对 B.2对 C.3对 D.4对
7.如图所示的四边形均为矩形或正方形,下列等式能够正确表示该图形面积关系的是( )
A. B.
C. D.
8.若多项式是完全平方式,则的值为( )
A.4 B. C. D.
9.参加“绿化家园”活动,已知乙班同学每小时比甲班多种2棵树,甲班同学种20棵树与乙班种26棵树所用的时间相同.设甲班每小时种棵树,则列出的方程是( )
A. B. C. D.
10.如图,已知,点D、E分别在、上且,连接交于点M,连接,过点A分别作,垂足分别为F、G,下列结论:①;②;③平分;④如果,则E是的中点;其中正确结论的个数为( )
A.1个 B.2个 C.3个 D.4个
二、填空题
11.已知三角形两边的长分别为1和3,第三边长为整数,则第三边的长为 .
12.在中,,的外角等于,则的度数是 .
13.如图,要测量河岸相对两点A,B的距离,可以从AB的垂线BF上取两点C,D.使BC=CD,过D作DE⊥BF,且A,C,E三点在一直线上.若测得DE=30米,则AB= 米.
14.如图,边长分别为a,b的长方形,它的周长为15,面积为10,则= .
15.若的展开式中不含x的一次项,则m=
16.如图,,,,则 .
17.如图,在中,,,,分别是边,,上的点,且,.若,则的度数为 °.
18.如图,在中,,,为边上的垂直平分线,若点D在直线上,连接,,则周长的最小值为 .
三、解答题
19.化简:
(1) (2)
20.化简分式,并在、、、、中选一个你喜欢的数作为的值,求代数式的值
21.解下列分式方程:
(1); (2).
22.如图,在平面直角坐标系中,,,.
(1)请画出关于y轴对称的;(其中,,分别是A,B,C的对应点,不写画法)
(2)直接写出,,三点的坐标:
(_____,_____), (_____,_____), (_____,_____);
(3)的面积=________.
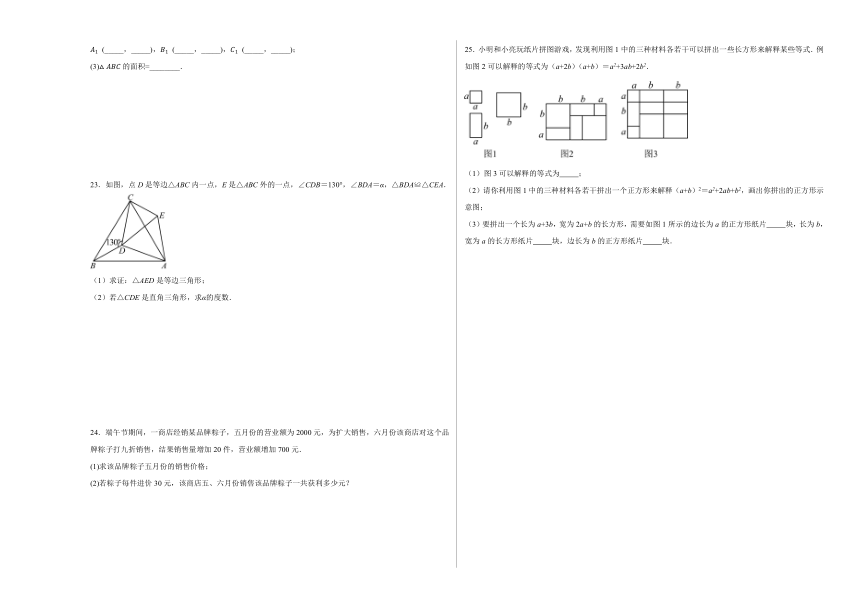
23.如图,点D是等边△ABC内一点,E是△ABC外的一点,∠CDB=130°,∠BDA=α,△BDA≌△CEA.
(1)求证:△AED是等边三角形;
(2)若△CDE是直角三角形,求α的度数.
24.端午节期间,一商店经销某品牌粽子,五月份的营业额为2000元,为扩大销售,六月份该商店对这个品牌粽子打九折销售,结果销售量增加20件,营业额增加700元.
(1)求该品牌粽子五月份的销售价格;
(2)若粽子每件进价30元,该商店五、六月份销售该品牌粽子一共获利多少元?
25.小明和小亮玩纸片拼图游戏,发现利用图1中的三种材料各若干可以拼出一些长方形来解释某些等式.例如图2可以解释的等式为(a+2b)(a+b)=a2+3ab+2b2.
(1)图3可以解释的等式为 ;
(2)请你利用图1中的三种材料各若干拼出一个正方形来解释(a+b)2=a2+2ab+b2,画出你拼出的正方形示意图;
(3)要拼出一个长为a+3b,宽为2a+b的长方形,需要如图1所示的边长为a的正方形纸片 块,长为b,宽为a的长方形纸片 块,边长为b的正方形纸片 块.
参考答案:
题号 1 2 3 4 5 6 7 8 9 10
答案 B B B C B D C C D D
11.3
12.
13.30.
14.225
15.10.
16.
17.
18.12
19.(1)
;
(2)
.
20.解:原式= -3
= -3
=-3
当=1时,原式=1-3=-2.
21.(1)解:方程两边同乘以,
得:,
解得:,
检验:当时,,
∴原方程的解是;
(2)方程两边同乘以,
得:,
解得:,
检验:当时,,
∴是原方程的增根,
∴原方程无解.
22.(1)解:如图
为所求作;
(2)解:由(1)图得
,,
故答案:,;,;,;
(3)解:由题意得
;
23.解:(1)∵,,
∴,,,
∴,
∴,
∵是等边三角形,
∴,
∴,
∵,
∴是等边三角形;
(2)∵是等边三角形,
∴,
∵,∠BDA=α,
∴,,
.
∵是直角三角形,.
当时, ,
∴,
当,,
∴,
∴或.
24.(1)解:设该品牌粽子五月份的销售价格为x元,
依题得:,
解得,
经检验,是原方程的解,
答:该品牌粽子五月份的销售价格为50元;
(2)解:五月份的销售量:(件),销售额为:2000元,
则六月份的销售量为:(件),销售额为:(元),
则总利润为:(元),
答:该商店五、六月份销售该品牌粽子一共获利1700元.
25.解:(1)图3的面积可以用(a+2b)(2a+b)表示,也可以用2a2+5ab+2b2表示,因此有(a+2b)(2a+b)=2a2+5ab+2b2,
故答案为:(a+2b)(2a+b)=2a2+5ab+2b2;
(2)(a+b)2=a2+2ab+b2,用图形表示如图所示:
(3)由于(a+3b)(2a+b)=2a2+7ab+3b2,因此需要边长为a的正方形纸片2张,长为b、宽为a的长方形纸片7张,边长为b的正方形纸片3张,
学校:___________姓名:___________班级:___________学号:___________
一、单选题
1.以下是轴对称图形的是( )
A. B. C. D.
2.一种细胞的直径约为0.000052米,将0.000052用科学记数法表示为( )
A. B. C. D.
3.已知一个多边形的内角和是,则这个多边形是().
A.四边形 B.五边形 C.六边形 D.七边形
4.如图,在中,分别以点A,B为圆心,以大于的线段长为半径画弧,两弧分别相交于两侧的M,N两点,直线交于点D,交于点E,连接,平分.若,,则的面积为( ).
A.7 B.8 C.14 D.28
5.已知:,则a+的值为( )
A. B.1 C.-1 D.-5
6.如图,,垂足分别为D、E,相交于O点,,连接,则图中全等的三角形共有( )
A.1对 B.2对 C.3对 D.4对
7.如图所示的四边形均为矩形或正方形,下列等式能够正确表示该图形面积关系的是( )
A. B.
C. D.
8.若多项式是完全平方式,则的值为( )
A.4 B. C. D.
9.参加“绿化家园”活动,已知乙班同学每小时比甲班多种2棵树,甲班同学种20棵树与乙班种26棵树所用的时间相同.设甲班每小时种棵树,则列出的方程是( )
A. B. C. D.
10.如图,已知,点D、E分别在、上且,连接交于点M,连接,过点A分别作,垂足分别为F、G,下列结论:①;②;③平分;④如果,则E是的中点;其中正确结论的个数为( )
A.1个 B.2个 C.3个 D.4个
二、填空题
11.已知三角形两边的长分别为1和3,第三边长为整数,则第三边的长为 .
12.在中,,的外角等于,则的度数是 .
13.如图,要测量河岸相对两点A,B的距离,可以从AB的垂线BF上取两点C,D.使BC=CD,过D作DE⊥BF,且A,C,E三点在一直线上.若测得DE=30米,则AB= 米.
14.如图,边长分别为a,b的长方形,它的周长为15,面积为10,则= .
15.若的展开式中不含x的一次项,则m=
16.如图,,,,则 .
17.如图,在中,,,,分别是边,,上的点,且,.若,则的度数为 °.
18.如图,在中,,,为边上的垂直平分线,若点D在直线上,连接,,则周长的最小值为 .
三、解答题
19.化简:
(1) (2)
20.化简分式,并在、、、、中选一个你喜欢的数作为的值,求代数式的值
21.解下列分式方程:
(1); (2).
22.如图,在平面直角坐标系中,,,.
(1)请画出关于y轴对称的;(其中,,分别是A,B,C的对应点,不写画法)
(2)直接写出,,三点的坐标:
(_____,_____), (_____,_____), (_____,_____);
(3)的面积=________.
23.如图,点D是等边△ABC内一点,E是△ABC外的一点,∠CDB=130°,∠BDA=α,△BDA≌△CEA.
(1)求证:△AED是等边三角形;
(2)若△CDE是直角三角形,求α的度数.
24.端午节期间,一商店经销某品牌粽子,五月份的营业额为2000元,为扩大销售,六月份该商店对这个品牌粽子打九折销售,结果销售量增加20件,营业额增加700元.
(1)求该品牌粽子五月份的销售价格;
(2)若粽子每件进价30元,该商店五、六月份销售该品牌粽子一共获利多少元?
25.小明和小亮玩纸片拼图游戏,发现利用图1中的三种材料各若干可以拼出一些长方形来解释某些等式.例如图2可以解释的等式为(a+2b)(a+b)=a2+3ab+2b2.
(1)图3可以解释的等式为 ;
(2)请你利用图1中的三种材料各若干拼出一个正方形来解释(a+b)2=a2+2ab+b2,画出你拼出的正方形示意图;
(3)要拼出一个长为a+3b,宽为2a+b的长方形,需要如图1所示的边长为a的正方形纸片 块,长为b,宽为a的长方形纸片 块,边长为b的正方形纸片 块.
参考答案:
题号 1 2 3 4 5 6 7 8 9 10
答案 B B B C B D C C D D
11.3
12.
13.30.
14.225
15.10.
16.
17.
18.12
19.(1)
;
(2)
.
20.解:原式= -3
= -3
=-3
当=1时,原式=1-3=-2.
21.(1)解:方程两边同乘以,
得:,
解得:,
检验:当时,,
∴原方程的解是;
(2)方程两边同乘以,
得:,
解得:,
检验:当时,,
∴是原方程的增根,
∴原方程无解.
22.(1)解:如图
为所求作;
(2)解:由(1)图得
,,
故答案:,;,;,;
(3)解:由题意得
;
23.解:(1)∵,,
∴,,,
∴,
∴,
∵是等边三角形,
∴,
∴,
∵,
∴是等边三角形;
(2)∵是等边三角形,
∴,
∵,∠BDA=α,
∴,,
.
∵是直角三角形,.
当时, ,
∴,
当,,
∴,
∴或.
24.(1)解:设该品牌粽子五月份的销售价格为x元,
依题得:,
解得,
经检验,是原方程的解,
答:该品牌粽子五月份的销售价格为50元;
(2)解:五月份的销售量:(件),销售额为:2000元,
则六月份的销售量为:(件),销售额为:(元),
则总利润为:(元),
答:该商店五、六月份销售该品牌粽子一共获利1700元.
25.解:(1)图3的面积可以用(a+2b)(2a+b)表示,也可以用2a2+5ab+2b2表示,因此有(a+2b)(2a+b)=2a2+5ab+2b2,
故答案为:(a+2b)(2a+b)=2a2+5ab+2b2;
(2)(a+b)2=a2+2ab+b2,用图形表示如图所示:
(3)由于(a+3b)(2a+b)=2a2+7ab+3b2,因此需要边长为a的正方形纸片2张,长为b、宽为a的长方形纸片7张,边长为b的正方形纸片3张,
同课章节目录
