24.3正多边形和圆 课件(共28张PPT)
文档属性
| 名称 | 24.3正多边形和圆 课件(共28张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 414.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-04-16 13:57:09 | ||
图片预览


文档简介
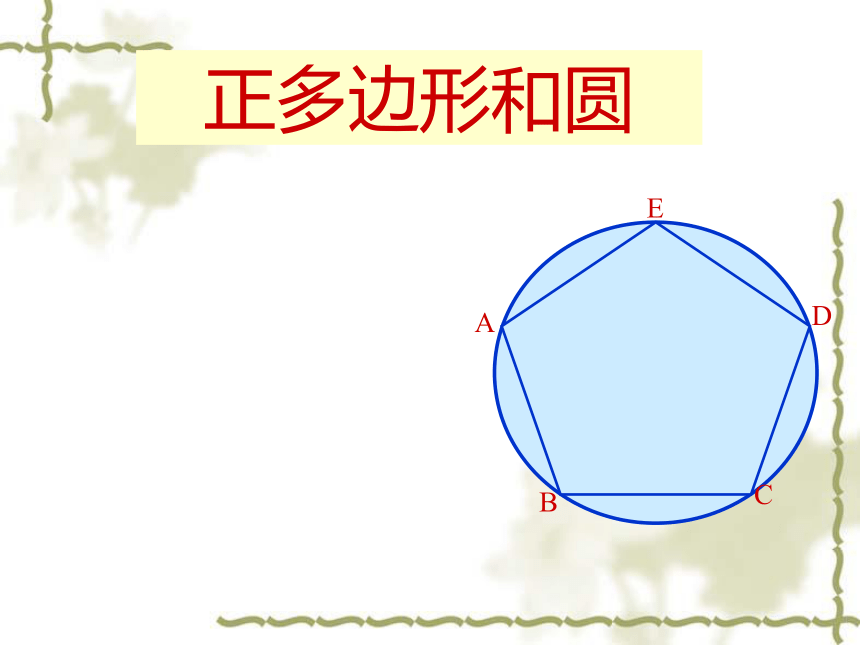
课件28张PPT。正多边形和圆ABCDE正多边形:
各边相等,各角也相等的多边形叫做正多边形。
正n边形:如果一个正多边形有n条边,那么这个正多边形叫做正n边形。三条边相等,三个角也相等(60度)。四条边都相等,四个角也相等(90度)。想一想:
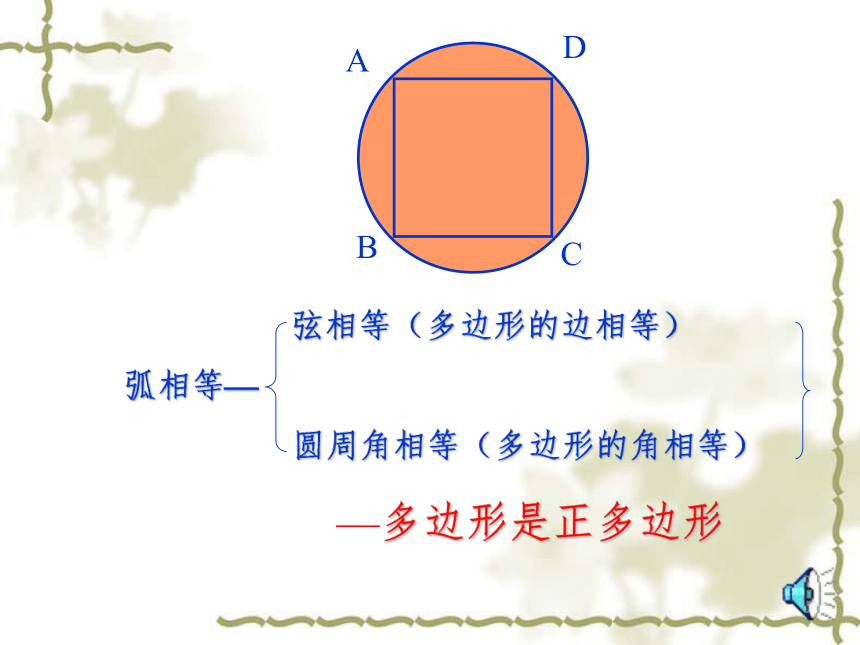
菱形是正多边形吗?矩形是正多边形吗?为什么? 弦相等(多边形的边相等)
弧相等—
圆周角相等(多边形的角相等) —多边形是正多边形ABCD⌒⌒⌒123ABCDE证明:∵AB=BC=CD=DE=EA
∴AB=BC=CD=DE=EA
∵BCE=CDA=3AB
∴∠1=∠2
同理∠2=∠3=∠4=∠5
又∵顶点A、B、C、D、E都在⊙O上,
∴五边形ABCDE是⊙O的内接五边形.
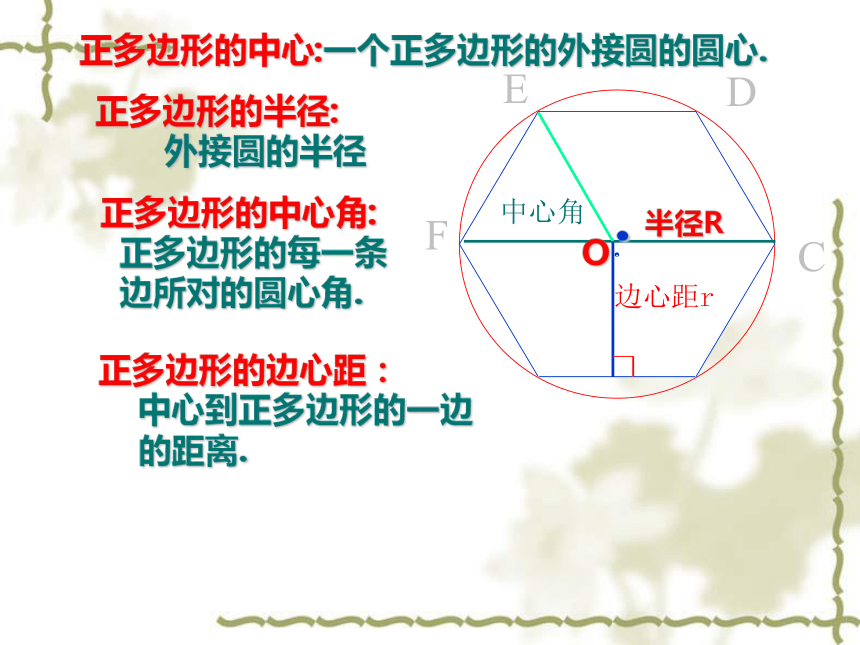
4⌒⌒5⌒⌒⌒⌒⌒⌒⌒⌒.O中心角半径R边心距r正多边形的中心:一个正多边形的外接圆的圆心.正多边形的半径:
外接圆的半径正多边形的中心角:
正多边形的每一条
边所对的圆心角.正多边形的边心距:
中心到正多边形的一边
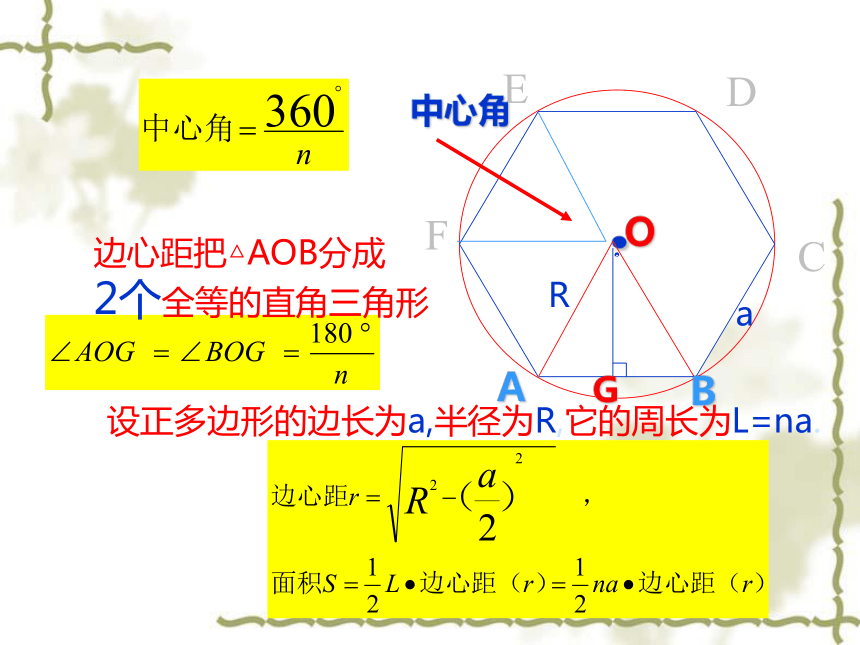
的距离..O中心角ABG边心距把△AOB分成
2个全等的直角三角形设正多边形的边长为a,半径为R,它的周长为L=na.Ra例 有一个亭子它的地基是半径为4m的正六边形,求
地基的周长和面积(精确到0.1平方米)..OBCrRP解:∴亭子的周长 L=6×4=24(m)正n边形的一个内角的度数是____________;
中心角是___________;
正多边形的中心角与外角的大小关系
是________.相等抢答题:1、O是正
圆与 圆的圆心。△ABC的中心,它是△ABC的2、OB叫正△ABC的 ,它是正△ABC的
圆的半径。 3、OD叫作正△ABC的 ,它是正△ABC的 圆的半径。D外接内切半径外接边心距内切4、正方形ABCD的外接圆圆心O叫做
正方形ABCD的5、正方形ABCD的内切圆的半径OE叫做
正方形ABCD的ABCD.OE中心边心距6、⊙O是正五边形ABCDE的外接圆,弦AB的
弦心距OF叫正五边形ABCDE的 ,
它是正五边形ABCDE的 圆的半径。7、 ∠AOB叫做正五边形ABCDE的 角,
它的度数是边心距内切中心72度8、图中正六边形ABCDEF的中心角是
它的度数是9、你发现正六边形ABCDEF的半径与边长具有
什么数量关系?为什么? BA∠AOB60度1、正多边形的各边相等2、正多边形的各角相等四、正多边形的性质:3、正多边形都是轴对称图形,一个正n边形
共有n条对称轴,每条对称轴都通过n边形
的中心。4、边数是偶数的正多边形还是中心
对称图形,它的中心就是对称中心。画正多边形的方法1.用量角器等分圆
2.尺规作图等分圆(1)正四、正八边形的尺规作图(2)正六、正三 、正十二边形的尺规作图 由于正多边形在生产、生活实际中有广泛的应用性,所以会画正多边形应是学生必备能力之一。
怎样画一个正多边形呢?
问题1:已知⊙O的半径为2cm,求作圆的内接正三角形.
120 °①用量角器度量,使∠AOB=∠BOC=∠COA=120°.
②用量角器或30°角的三角板度量,使∠BAO=∠CAO=30°.
AOCB 你能用以上方法画出正四边形、正五边形、正六边形吗?·ABCDOOABCDEF·90°72°60° 你能尺规作出正四边形、正八边形吗?·ABCDO只要作出已知⊙O的互相垂直的直径即得圆内接正方形,再过圆心作各边的垂线与⊙O相交,或作各中心角的角平分线与⊙O相交,即得圆接正八边形,照此方法依次可作正十六边形、正三十二边形、正六十四边形…… 你能尺规作出正六边形、正三角形、正十二边形吗?OABCEF·D 以半径长在圆周上截取六段相等的弧,依次连结各等分点,则作出正六边形.
先作出正六边形,则可作正三角形,正十二边形,正二十四边形……… 说说作正多边形的方法有哪些?归纳
(1)用量角器等分圆周作正n边形;
(2)用尺规作正方形及由此扩展作正八边形, 用尺规作正六边形及由此扩展作正12边形、正三角形. 练习: (1)用量角器作五角星;
(2)P116. 探究按照一定比例,画一个停车
让行的交通标志的外缘停ABCDEO如图:
已知点A、B、C、D、E是⊙O 的5等分点,画出⊙O的内接和外切正五边形小结:
1、怎样的多边形是正多边形?
你能举例说明吗?
2、怎样判定一个多边形是正多边形?各边相等,各角也相等的多边形叫做正多边形。
根据正多边形与圆关系的
第一个定理达标检测:
1、判断题。
①各边都相等的多边形是正多边形。 ( )
②一个圆有且只有一个内接正多边形。 ( )
2、证明题。
求证:顺次连结正六边形
各边中点所得的多
边形是正六边形。ABCDEF××
各边相等,各角也相等的多边形叫做正多边形。
正n边形:如果一个正多边形有n条边,那么这个正多边形叫做正n边形。三条边相等,三个角也相等(60度)。四条边都相等,四个角也相等(90度)。想一想:
菱形是正多边形吗?矩形是正多边形吗?为什么? 弦相等(多边形的边相等)
弧相等—
圆周角相等(多边形的角相等) —多边形是正多边形ABCD⌒⌒⌒123ABCDE证明:∵AB=BC=CD=DE=EA
∴AB=BC=CD=DE=EA
∵BCE=CDA=3AB
∴∠1=∠2
同理∠2=∠3=∠4=∠5
又∵顶点A、B、C、D、E都在⊙O上,
∴五边形ABCDE是⊙O的内接五边形.
4⌒⌒5⌒⌒⌒⌒⌒⌒⌒⌒.O中心角半径R边心距r正多边形的中心:一个正多边形的外接圆的圆心.正多边形的半径:
外接圆的半径正多边形的中心角:
正多边形的每一条
边所对的圆心角.正多边形的边心距:
中心到正多边形的一边
的距离..O中心角ABG边心距把△AOB分成
2个全等的直角三角形设正多边形的边长为a,半径为R,它的周长为L=na.Ra例 有一个亭子它的地基是半径为4m的正六边形,求
地基的周长和面积(精确到0.1平方米)..OBCrRP解:∴亭子的周长 L=6×4=24(m)正n边形的一个内角的度数是____________;
中心角是___________;
正多边形的中心角与外角的大小关系
是________.相等抢答题:1、O是正
圆与 圆的圆心。△ABC的中心,它是△ABC的2、OB叫正△ABC的 ,它是正△ABC的
圆的半径。 3、OD叫作正△ABC的 ,它是正△ABC的 圆的半径。D外接内切半径外接边心距内切4、正方形ABCD的外接圆圆心O叫做
正方形ABCD的5、正方形ABCD的内切圆的半径OE叫做
正方形ABCD的ABCD.OE中心边心距6、⊙O是正五边形ABCDE的外接圆,弦AB的
弦心距OF叫正五边形ABCDE的 ,
它是正五边形ABCDE的 圆的半径。7、 ∠AOB叫做正五边形ABCDE的 角,
它的度数是边心距内切中心72度8、图中正六边形ABCDEF的中心角是
它的度数是9、你发现正六边形ABCDEF的半径与边长具有
什么数量关系?为什么? BA∠AOB60度1、正多边形的各边相等2、正多边形的各角相等四、正多边形的性质:3、正多边形都是轴对称图形,一个正n边形
共有n条对称轴,每条对称轴都通过n边形
的中心。4、边数是偶数的正多边形还是中心
对称图形,它的中心就是对称中心。画正多边形的方法1.用量角器等分圆
2.尺规作图等分圆(1)正四、正八边形的尺规作图(2)正六、正三 、正十二边形的尺规作图 由于正多边形在生产、生活实际中有广泛的应用性,所以会画正多边形应是学生必备能力之一。
怎样画一个正多边形呢?
问题1:已知⊙O的半径为2cm,求作圆的内接正三角形.
120 °①用量角器度量,使∠AOB=∠BOC=∠COA=120°.
②用量角器或30°角的三角板度量,使∠BAO=∠CAO=30°.
AOCB 你能用以上方法画出正四边形、正五边形、正六边形吗?·ABCDOOABCDEF·90°72°60° 你能尺规作出正四边形、正八边形吗?·ABCDO只要作出已知⊙O的互相垂直的直径即得圆内接正方形,再过圆心作各边的垂线与⊙O相交,或作各中心角的角平分线与⊙O相交,即得圆接正八边形,照此方法依次可作正十六边形、正三十二边形、正六十四边形…… 你能尺规作出正六边形、正三角形、正十二边形吗?OABCEF·D 以半径长在圆周上截取六段相等的弧,依次连结各等分点,则作出正六边形.
先作出正六边形,则可作正三角形,正十二边形,正二十四边形……… 说说作正多边形的方法有哪些?归纳
(1)用量角器等分圆周作正n边形;
(2)用尺规作正方形及由此扩展作正八边形, 用尺规作正六边形及由此扩展作正12边形、正三角形. 练习: (1)用量角器作五角星;
(2)P116. 探究按照一定比例,画一个停车
让行的交通标志的外缘停ABCDEO如图:
已知点A、B、C、D、E是⊙O 的5等分点,画出⊙O的内接和外切正五边形小结:
1、怎样的多边形是正多边形?
你能举例说明吗?
2、怎样判定一个多边形是正多边形?各边相等,各角也相等的多边形叫做正多边形。
根据正多边形与圆关系的
第一个定理达标检测:
1、判断题。
①各边都相等的多边形是正多边形。 ( )
②一个圆有且只有一个内接正多边形。 ( )
2、证明题。
求证:顺次连结正六边形
各边中点所得的多
边形是正六边形。ABCDEF××
同课章节目录
