江苏省如皋市四校09-10学年高二上学期期中联考试题(数学文)
文档属性
| 名称 | 江苏省如皋市四校09-10学年高二上学期期中联考试题(数学文) |

|
|
| 格式 | rar | ||
| 文件大小 | 181.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-11-17 00:00:00 | ||
图片预览


文档简介
如皋市四校09-10学年高二上学期期中联考试题
数学(文科)
命题人:薛中 朱小平 审核人:薛中 陆建进
参考公式:
锥体体积公式V=Sh 球的表面积公式 球的体积公式 R为半径
一、填空题:本大题共14小题,每小题5分,共70分。
1、抛物线的焦点坐标是 ;
2、若关于的方程表示的曲线为焦点在x轴上的椭圆,则的取值范围为 ;
3、如图所示的等腰直角三角形,表示一个水平放置的平面图形的平面直观图,则这个平面图形的面积是 .
4、已知空间直角坐标系中点,且点在三个坐标平面平面,平面,平面上的射影的坐标依次为,和,则的值为 ;
5、已知一个空间几何体的三视图如图所示,根据图中标出的尺寸,可得到这个几何体的体积是__________.(结果用表示)
6、如右上图,正方体,点M是的中点,点O是底面的中心,P是上的任意一点,则直线BM与OP所成的角大小为 ;
7、一个棱长为1正方体的各顶点均在同一球的球面上,则此球的表面积为 ;
8、为不重合的平面,表示直线,下列叙述正确的序号是 。
① 若,则PQ;②若,,则且; ③ 若∥且∥,则∥;④ 若,则。
9、双曲线离心率为,则此双曲线的渐近线方程为 ;
10、以椭圆的焦点为顶点、两顶点为焦点的双曲线标准方程是 ;
11、将圆上所有点的纵坐标保持不变,横坐标变为原来的一半,则所得曲线的离心率为 ;
12、有一根高为,底面半径为的圆柱形铁管,用一段铁丝在铁管上缠绕2圈,并使铁丝的两个端点落在圆柱的同一母线的两端,则铁丝的最短长度为 (结果用表示)。
13、设是空间不同的直线或不同的平面,且直线不在平面内,在下列几个条件中,能保证“若x⊥z且y⊥z,则x∥y”正确序号的有 。
①x为直线,y、z是平面; ②x、y、z均为平面;
③x、y为直线,z为平面; ④x、y为平面, z为直线;
14、有一只(底面圆半径是2 )装有半杯水的圆柱形透明水杯竖直放在水平桌面上,现将水杯轻轻向一侧倾斜,使得圆柱母线与桌面成角,这时杯中水平水面截杯壁所得的椭圆的焦距大小(不考虑杯壁厚度)是 。
二.解答题:本大题共6小题,共90分.解答应写出文字说明,证明过程或演算步骤.
15、(本小题满分14分)如图,在正方体中,点E、F分别是的中点,
(1) 求证:点共面;
(2)连结并延长交的延长线于,连结并延长交的延长线于,求证:共线。
16、(本小题满分14分)如图,一种电影放映灯泡的反射镜面是旋转椭圆面(椭圆绕其对称轴旋转一周形成的曲面)的一部分。过对称轴的截口BAC是椭圆的一部分,灯丝位于椭圆的一个焦点上,片门位于另一个焦点上。由椭圆一个焦点发出的光线,经过旋转椭圆面反射后集中到另一个焦点。已知,= , ,建立适当的平面直角坐标系,求截口BAC所在椭圆的方程。
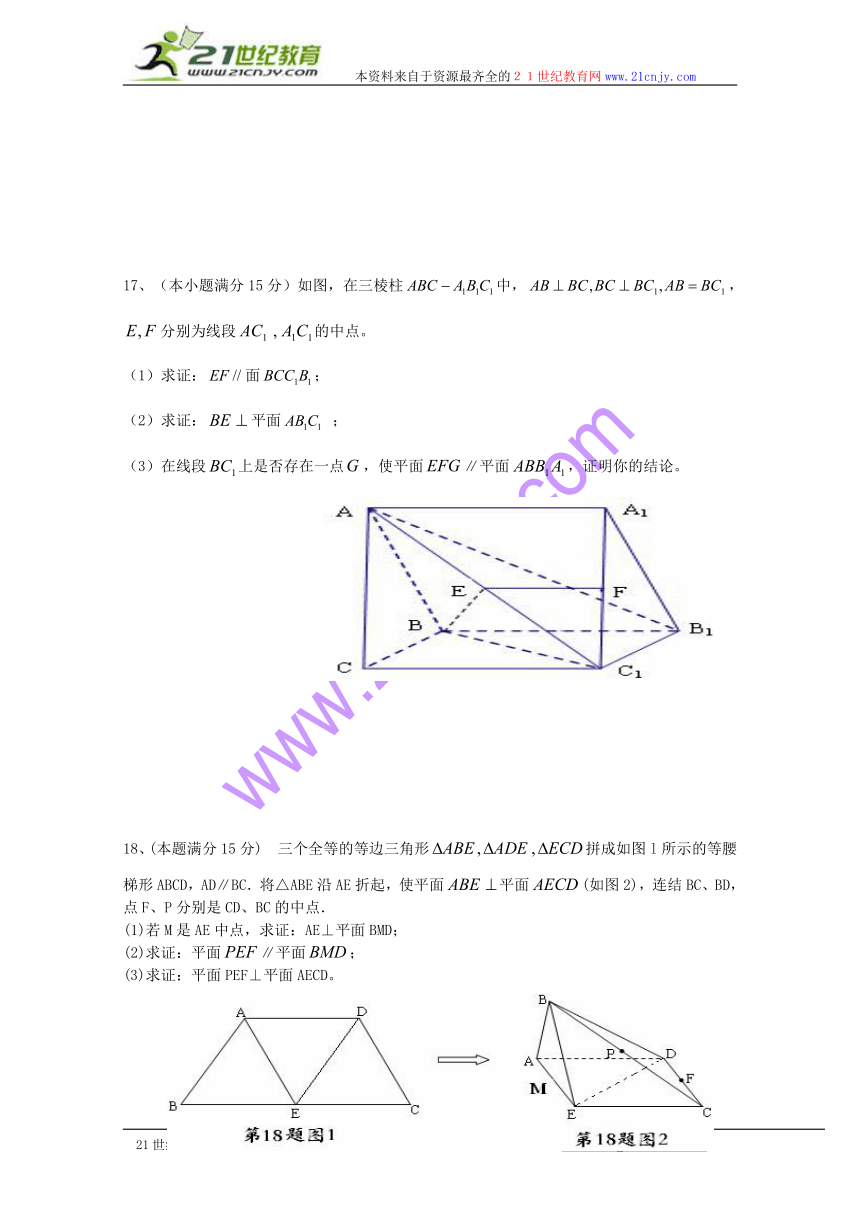
17、(本小题满分15分)如图,在三棱柱中,,分别为线段的中点。
(1)求证:面;
(2)求证:平面 ;
(3)在线段上是否存在一点,使平面∥平面,证明你的结论。
18、(本题满分15分) 三个全等的等边三角形拼成如图l所示的等腰梯形ABCD,AD∥BC.将△ABE沿AE折起,使平面平面(如图2),连结BC、BD,点F、P分别是CD、BC的中点.
(1)若M是AE中点,求证:AE⊥平面BMD;
(2)求证:平面∥平面;
(3)求证:平面PEF⊥平面AECD。
19、 (本题满分18分)已知点是椭圆上一动点,点是椭圆的左右两焦点。
(1)求该椭圆的长轴长、右准线方程;
(2)一抛物线以椭圆的中心为顶点、椭圆的右准线为准线,求抛物线标准方程;(3)当时,求的面积;
(4)点是圆:上一动点,求的最小值。
20、(本题满分14分)已知椭圆C方程为,椭圆C与直线交与A、B两点,以线段AB为直径的圆M过坐标原点,直线过圆心M. (1)试判断与是否垂直,并说明理由; (2)求椭圆C的方程。
如皋市四校09-10学年高二上学期期中联考试题
数学文参考答案
填空题
1. 2. 3. 4. 0 5.
6. () 7. 8. ① ② ③ 9. 10.
11. 12. 13. ①、③、④ 14.
二、解答题
15.证明:(1)取中点G,因为E、G分别为AA1,B1B的中点,所以四边形AEGB1为平行四边形, ,又,所以,即四边形EGC1D1为平行四边形,所以,又四边形C1GBF为平行四边形,C1G∥BF,所以BF∥D1E,所以点D1、E、F、B共面……………7分
(2)由(1)得D1、E、F、B共面,设平面D1EFB平面ABCD=,则B,
又M= D1EDA,所以M平面D1EFB,且M平面ABCD,所以M,同理N
所以M、B、N都在直线上,即M、B、N共线。…14分
16.解:建立如图所示的直角坐标系…………3分
设所求椭圆方程()…5分
(或) ……10分
解得………………13分
所求椭圆方程………14分
注:学生将用根式表示同样得满分。
17.(1),
,
面;………………5分
(2)
………………………………………………10分
(3)G为中点………………………………………………11分
…………………………………………15分
18、证明:(1)取中点,连接. 与都是等边三角形
平面
平面………………………………………………5分
(2)证明:可证AECD为平行四边形,可证EF∥MD,PF∥BD;
可证,又PF、EF相交,所以得证。……5分
(3)
…………………………………………………………………………………………15分
注:用第二问结论参照得分。
19、(本题满分18分)
解:(1)长轴长26,右准线方程………4分
(2)抛物线……………………8分
(3)设,由题意知,………………11分
…………13分
(4)最小值为21…………………………18分
20. (本题满14分)
解:(1)由于AB是圆M的直径,O点在圆上,
所以是直角,与垂直………3分
(2)设, ………………4分
由………………6分
得
所以……………………8分
…………………10分
又……………12分
解得……………13分
所以椭圆方程为……………14分
注:学生有其它几种解法参照得分。
数学(文科)
命题人:薛中 朱小平 审核人:薛中 陆建进
参考公式:
锥体体积公式V=Sh 球的表面积公式 球的体积公式 R为半径
一、填空题:本大题共14小题,每小题5分,共70分。
1、抛物线的焦点坐标是 ;
2、若关于的方程表示的曲线为焦点在x轴上的椭圆,则的取值范围为 ;
3、如图所示的等腰直角三角形,表示一个水平放置的平面图形的平面直观图,则这个平面图形的面积是 .
4、已知空间直角坐标系中点,且点在三个坐标平面平面,平面,平面上的射影的坐标依次为,和,则的值为 ;
5、已知一个空间几何体的三视图如图所示,根据图中标出的尺寸,可得到这个几何体的体积是__________.(结果用表示)
6、如右上图,正方体,点M是的中点,点O是底面的中心,P是上的任意一点,则直线BM与OP所成的角大小为 ;
7、一个棱长为1正方体的各顶点均在同一球的球面上,则此球的表面积为 ;
8、为不重合的平面,表示直线,下列叙述正确的序号是 。
① 若,则PQ;②若,,则且; ③ 若∥且∥,则∥;④ 若,则。
9、双曲线离心率为,则此双曲线的渐近线方程为 ;
10、以椭圆的焦点为顶点、两顶点为焦点的双曲线标准方程是 ;
11、将圆上所有点的纵坐标保持不变,横坐标变为原来的一半,则所得曲线的离心率为 ;
12、有一根高为,底面半径为的圆柱形铁管,用一段铁丝在铁管上缠绕2圈,并使铁丝的两个端点落在圆柱的同一母线的两端,则铁丝的最短长度为 (结果用表示)。
13、设是空间不同的直线或不同的平面,且直线不在平面内,在下列几个条件中,能保证“若x⊥z且y⊥z,则x∥y”正确序号的有 。
①x为直线,y、z是平面; ②x、y、z均为平面;
③x、y为直线,z为平面; ④x、y为平面, z为直线;
14、有一只(底面圆半径是2 )装有半杯水的圆柱形透明水杯竖直放在水平桌面上,现将水杯轻轻向一侧倾斜,使得圆柱母线与桌面成角,这时杯中水平水面截杯壁所得的椭圆的焦距大小(不考虑杯壁厚度)是 。
二.解答题:本大题共6小题,共90分.解答应写出文字说明,证明过程或演算步骤.
15、(本小题满分14分)如图,在正方体中,点E、F分别是的中点,
(1) 求证:点共面;
(2)连结并延长交的延长线于,连结并延长交的延长线于,求证:共线。
16、(本小题满分14分)如图,一种电影放映灯泡的反射镜面是旋转椭圆面(椭圆绕其对称轴旋转一周形成的曲面)的一部分。过对称轴的截口BAC是椭圆的一部分,灯丝位于椭圆的一个焦点上,片门位于另一个焦点上。由椭圆一个焦点发出的光线,经过旋转椭圆面反射后集中到另一个焦点。已知,= , ,建立适当的平面直角坐标系,求截口BAC所在椭圆的方程。
17、(本小题满分15分)如图,在三棱柱中,,分别为线段的中点。
(1)求证:面;
(2)求证:平面 ;
(3)在线段上是否存在一点,使平面∥平面,证明你的结论。
18、(本题满分15分) 三个全等的等边三角形拼成如图l所示的等腰梯形ABCD,AD∥BC.将△ABE沿AE折起,使平面平面(如图2),连结BC、BD,点F、P分别是CD、BC的中点.
(1)若M是AE中点,求证:AE⊥平面BMD;
(2)求证:平面∥平面;
(3)求证:平面PEF⊥平面AECD。
19、 (本题满分18分)已知点是椭圆上一动点,点是椭圆的左右两焦点。
(1)求该椭圆的长轴长、右准线方程;
(2)一抛物线以椭圆的中心为顶点、椭圆的右准线为准线,求抛物线标准方程;(3)当时,求的面积;
(4)点是圆:上一动点,求的最小值。
20、(本题满分14分)已知椭圆C方程为,椭圆C与直线交与A、B两点,以线段AB为直径的圆M过坐标原点,直线过圆心M. (1)试判断与是否垂直,并说明理由; (2)求椭圆C的方程。
如皋市四校09-10学年高二上学期期中联考试题
数学文参考答案
填空题
1. 2. 3. 4. 0 5.
6. () 7. 8. ① ② ③ 9. 10.
11. 12. 13. ①、③、④ 14.
二、解答题
15.证明:(1)取中点G,因为E、G分别为AA1,B1B的中点,所以四边形AEGB1为平行四边形, ,又,所以,即四边形EGC1D1为平行四边形,所以,又四边形C1GBF为平行四边形,C1G∥BF,所以BF∥D1E,所以点D1、E、F、B共面……………7分
(2)由(1)得D1、E、F、B共面,设平面D1EFB平面ABCD=,则B,
又M= D1EDA,所以M平面D1EFB,且M平面ABCD,所以M,同理N
所以M、B、N都在直线上,即M、B、N共线。…14分
16.解:建立如图所示的直角坐标系…………3分
设所求椭圆方程()…5分
(或) ……10分
解得………………13分
所求椭圆方程………14分
注:学生将用根式表示同样得满分。
17.(1),
,
面;………………5分
(2)
………………………………………………10分
(3)G为中点………………………………………………11分
…………………………………………15分
18、证明:(1)取中点,连接. 与都是等边三角形
平面
平面………………………………………………5分
(2)证明:可证AECD为平行四边形,可证EF∥MD,PF∥BD;
可证,又PF、EF相交,所以得证。……5分
(3)
…………………………………………………………………………………………15分
注:用第二问结论参照得分。
19、(本题满分18分)
解:(1)长轴长26,右准线方程………4分
(2)抛物线……………………8分
(3)设,由题意知,………………11分
…………13分
(4)最小值为21…………………………18分
20. (本题满14分)
解:(1)由于AB是圆M的直径,O点在圆上,
所以是直角,与垂直………3分
(2)设, ………………4分
由………………6分
得
所以……………………8分
…………………10分
又……………12分
解得……………13分
所以椭圆方程为……………14分
注:学生有其它几种解法参照得分。
同课章节目录
