江苏省如皋市四校09-10学年高二上学期期中联考试题(数学理)
文档属性
| 名称 | 江苏省如皋市四校09-10学年高二上学期期中联考试题(数学理) |

|
|
| 格式 | rar | ||
| 文件大小 | 182.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-11-17 00:00:00 | ||
图片预览

文档简介
如皋市四校09-10学年高二上学期期中联考试题
数学(理科)
命题人:薛中 陆建进 审核人:薛中 朱小平
参考公式:
锥体体积公式V=Sh 直棱柱侧面积公式S=ch
台体体积公式V=h(S上底+S下底+)
球的表面积、体积公式 ,其中R为球的半径
填空题:本大题共14小题,每小题5分,共70分。
1、命题“”的否定是_ ____.
2、已知点,且该点在三个坐标平面平面,平面,平面上的射影的坐标依次为,和,则的值为 .
3、如图所示的等腰直角三角形表示一个水平放置的平面图形的
直观图,则这个平面图形的面积是 _ ____.
4、设为不重合的三个平面,表示直线,下列叙述正确的序号是 _ ___.
① 若,则PQ;
②若,,则且;
③ 若∥且∥,则∥;
④ 若,则。
第8题图
5、设A是C的充分必要条件,B是C的充分条件,D是C的必要条件,D是B的充分条件,那么A是B的__ _____条件
6、一个长方体的各顶点均在同一球的球面上,且一个顶点上的三条棱的长分别为1,2,3,则此球的表面积为_ ____.
7、已知=(1,-1,3),=(-1,4,-2),=(7,5,λ),若、、三向量共面,则实数λ等于 .
8、如右上图,正方体,点M是的中点,点O是底面的中心,
P是上的任意一点,则直线BM与OP所成的角大小为 __
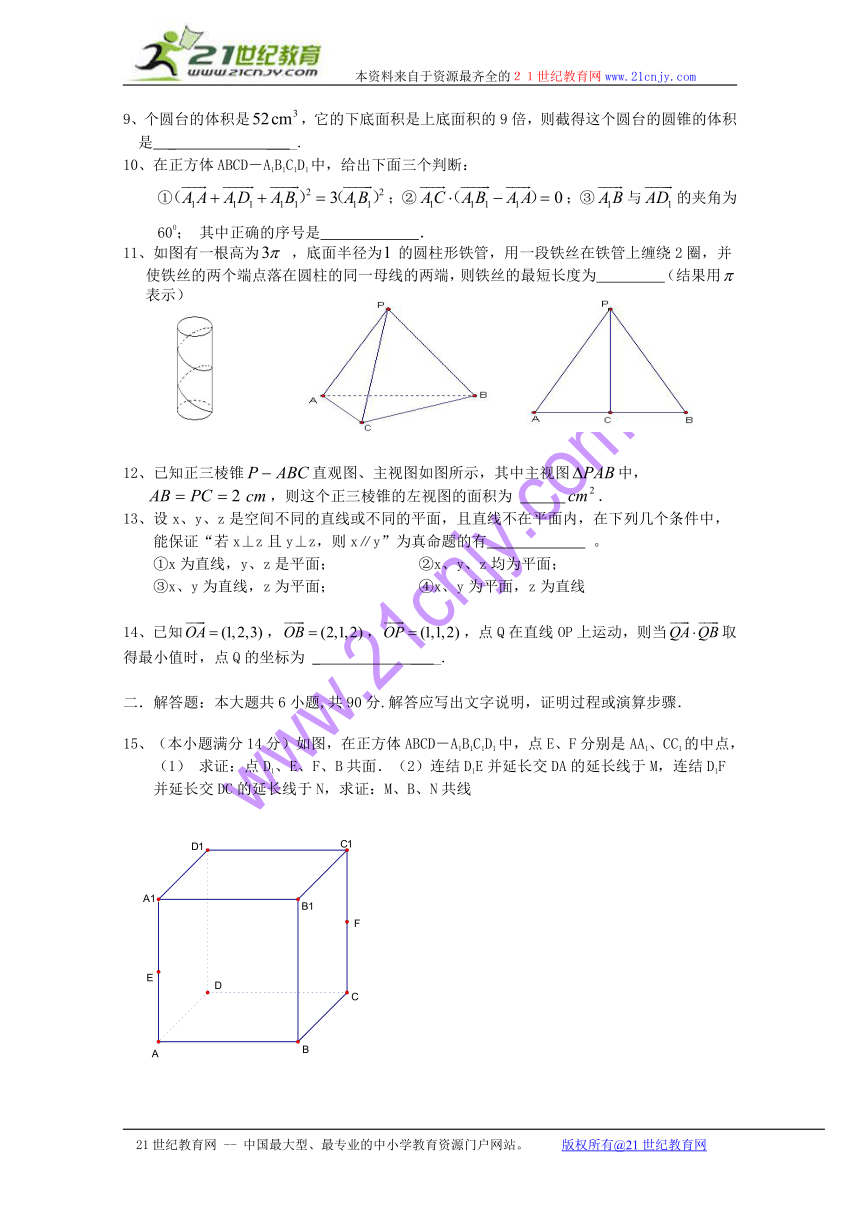
9、个圆台的体积是,它的下底面积是上底面积的9倍,则截得这个圆台的圆锥的体积是 _ ____.
10、在正方体ABCD-A1B1C1D1中,给出下面三个判断:
①;②;③与的夹角为600; 其中正确的序号是 .
11、如图有一根高为,底面半径为的圆柱形铁管,用一段铁丝在铁管上缠绕2圈,并使铁丝的两个端点落在圆柱的同一母线的两端,则铁丝的最短长度为 (结果用表示)
12、已知正三棱锥直观图、主视图如图所示,其中主视图中,,则这个正三棱锥的左视图的面积为 .
13、设x、y、z是空间不同的直线或不同的平面,且直线不在平面内,在下列几个条件中,能保证“若x⊥z且y⊥z,则x∥y”为真命题的有 。
①x为直线,y、z是平面; ②x、y、z均为平面;
③x、y为直线,z为平面; ④x、y为平面,z为直线
14、已知,,,点Q在直线OP上运动,则当取得最小值时,点Q的坐标为 _ ____.
二.解答题:本大题共6小题,共90分.解答应写出文字说明,证明过程或演算步骤.
15、(本小题满分14分)如图,在正方体ABCD-A1B1C1D1中,点E、F分别是AA1、CC1的中点,(1) 求证:点D1、E、F、B共面.(2)连结D1E并延长交DA的延长线于M,连结D1F并延长交DC的延长线于N,求证:M、B、N共线
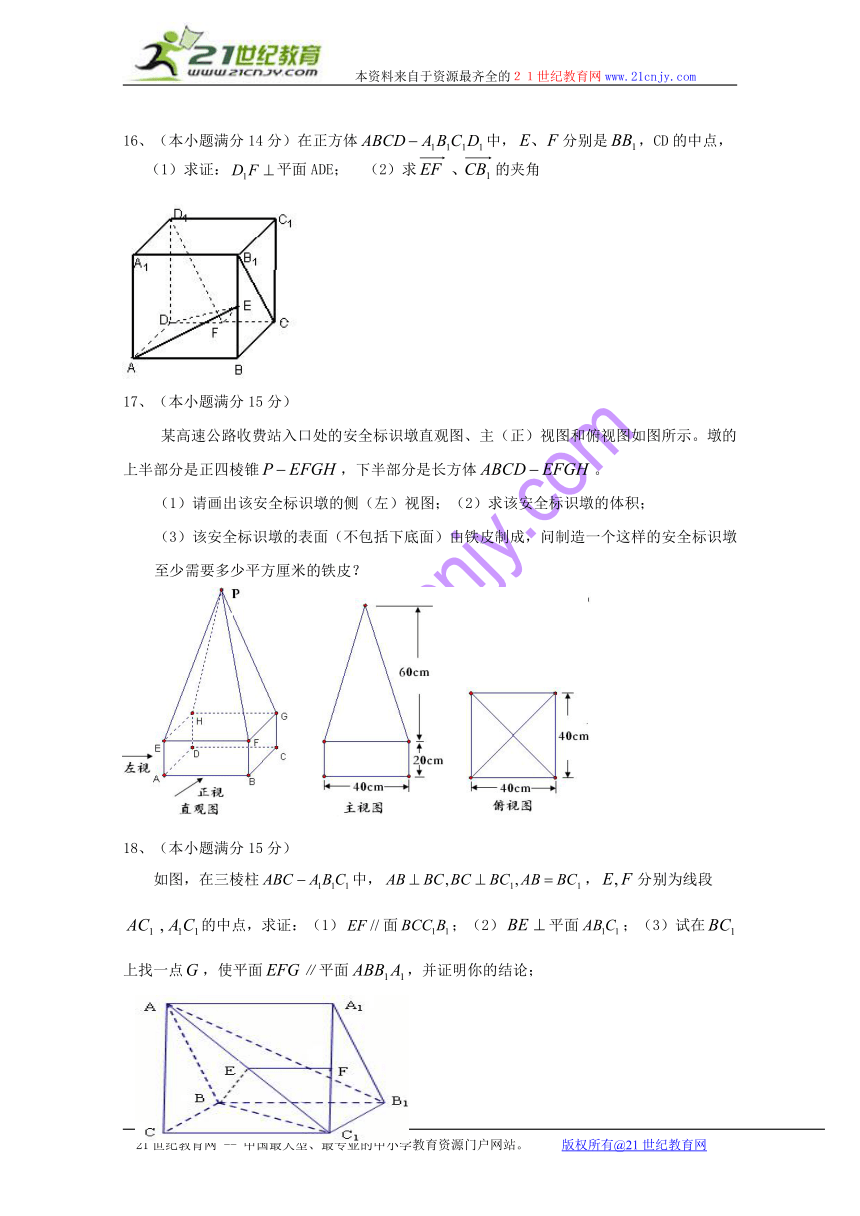
16、(本小题满分14分)在正方体中,分别是,CD的中点,
(1)求证:平面ADE; (2)求的夹角
17、(本小题满分15分)
某高速公路收费站入口处的安全标识墩直观图、主(正)视图和俯视图如图所示。墩的上半部分是正四棱锥,下半部分是长方体。
(1)请画出该安全标识墩的侧(左)视图;(2)求该安全标识墩的体积;
(3)该安全标识墩的表面(不包括下底面)由铁皮制成,问制造一个这样的安全标识墩至少需要多少平方厘米的铁皮?
18、(本小题满分15分)
如图,在三棱柱中,,分别为线段的中点,求证:(1)面;(2)平面;(3)试在上找一点,使平面∥平面,并证明你的结论;
19、(本小题满分16分)
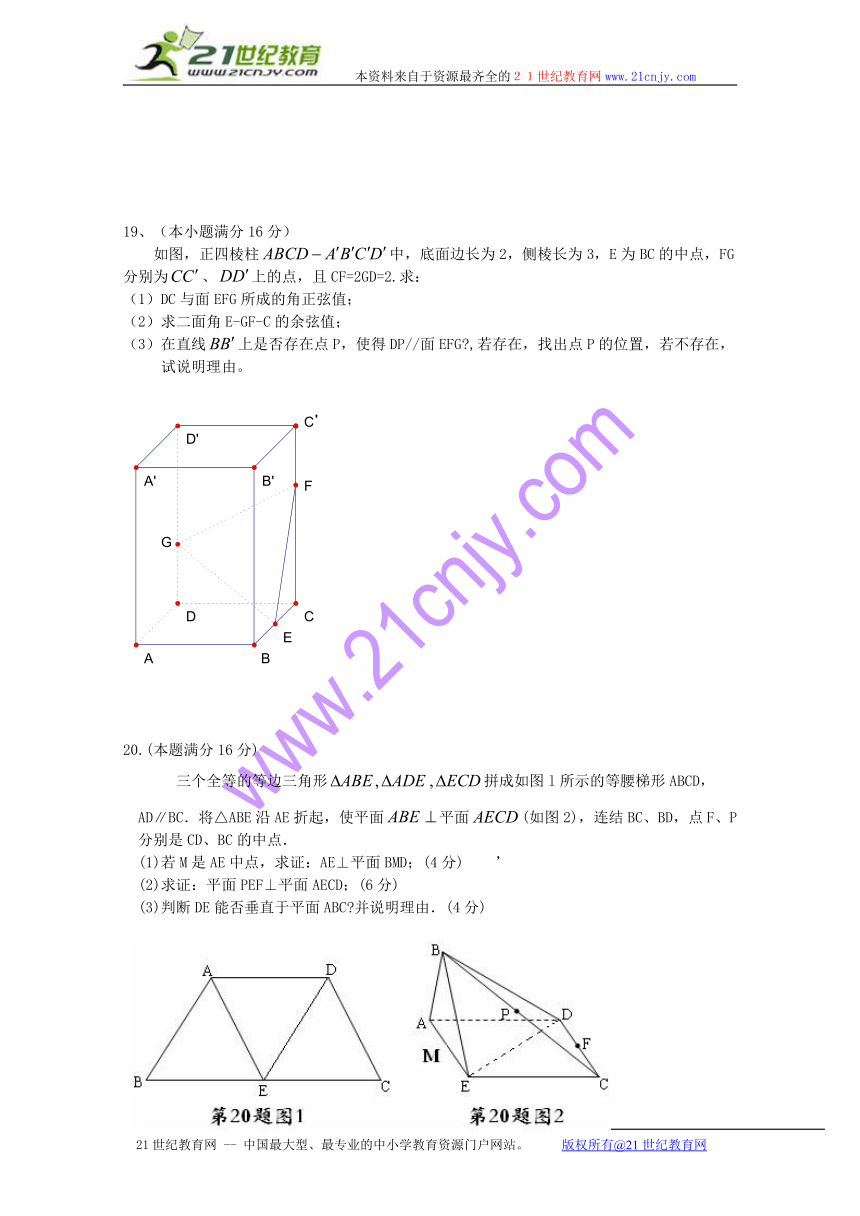
如图,正四棱柱中,底面边长为2,侧棱长为3,E为BC的中点,FG分别为、上的点,且CF=2GD=2.求:
(1)DC与面EFG所成的角正弦值;
(2)求二面角E-GF-C的余弦值;
(3)在直线上是否存在点P,使得DP//面EFG?,若存在,找出点P的位置,若不存在,试说明理由。
20.(本题满分16分)
三个全等的等边三角形拼成如图l所示的等腰梯形ABCD,AD∥BC.将△ABE沿AE折起,使平面平面(如图2),连结BC、BD,点F、P分别是CD、BC的中点.
(1)若M是AE中点,求证:AE⊥平面BMD;(4分) ’
(2)求证:平面PEF⊥平面AECD;(6分)
(3)判断DE能否垂直于平面ABC?并说明理由.(4分)
如皋市四校09-10学年高二上学期期中联考试题
高二数学参考答案及评分标准
填空题
1. 2. 0 3. 4. _① 、 ② 、③ 5. _充要
6. 7. 25 8. 9. 54 10. ① 、 ② 11. 5 12. 13. ①、③、④ 14.
二、解答题
15.(本题满分14分)
证明:(1)取中点G,因为E、G分别为AA1,B1B的中点,所以四边形AEGB1为平行四边形, ,又,所以,即四边形EGC1D1为平行四边形,所以,又四边形BGFC1为平行四边形,C1G∥BF,所以BF∥D1E,所以点D1、E、F、B共面……………7分
(2)由(1)得D1、E、F、B共面,设平面D1EFB平面ABCD=,则B,
又M= D1EDA,所以M平面D1EFB,且M平面ABCD,所以M,同理N
所以M、B、N都在直线上,即M、B、N共线。……………14分
16.解:建立如图所示的直角坐标系……………………………………………………1分
(1)不妨设正方体的棱长为1,
则D(0,0,0),A(1,0,0),(0,0,1),
E(1,1,),F(0,,0),
则=(0,,-1),=(1,0,0),
=(0,1,),
则=0,
=0,
,.
平面ADE. ………………………………………7分
(2)(1,1,1),C(0,1,0),
故=(1,0,1),=(-1,-,-),…………………9分
=-1+0-=-,
,,
则cos. ……… ………13分
…………………………………………………14分
17(本题满分15分).
(1)侧视图同正视图,如下图所示. ………………4分
(2)该安全标识墩的体积为:
…………………………………………………9分
(3)由题意知正四棱锥的斜高为…………………………………………………12分
所以表面积
答:略…………………………………………………15分
18.(本题满分15分)
(1),
,
面;………………4分
(2)
………………………………………………9分
(3)G为中点………………………………………………10分
………………………………………………………………………15分
19. (本题满16分)
解:(1)如图,以D为原点建立空间直角坐标系
则E(1,2,0),F(0,2,2),G(0,0,1)
∴=(-1,0,2),=(0,-2,-1),
设=(x,y,z)为面EFG的法向量,则
=0,=0,x=2z,z=-2y,取y=1,
得=(-4,1,-2) …………………………4分
=(0,2,0),设DC与面EFG所成的角为θ,
则,=…………………………7分
(2)设二面角E-GF-C的平面角为
易知=(2,0,0)为面的法向量…………………………………8分
二面角E-GF-C的余弦值为………………………………………………11分
(3)存在点P,在B点下方且BP=3, …………………………………13分
假设存在点P(2,2,x)使得DP//面EFG
由 =0得 x=-3
所以:存在点P,在B点下方且BP=3,此时P(2,2,-3)
=(2,2,-3),∴=0,∴DP//面EFG ……………………………………16分
20. (本题满分16分)
证明:(1)取中点,连接.
与都是等边三角形
平面
平面………………………………………………4分
(2)证明:
…………………………………………………………………………………………10分
(3)与平面不垂直.………………………………………………11分
证明:假设平面, 则
平面
,平面 平面
,这与矛盾
与平面不垂直.
…………………………………………………………………………………16分
数学(理科)
命题人:薛中 陆建进 审核人:薛中 朱小平
参考公式:
锥体体积公式V=Sh 直棱柱侧面积公式S=ch
台体体积公式V=h(S上底+S下底+)
球的表面积、体积公式 ,其中R为球的半径
填空题:本大题共14小题,每小题5分,共70分。
1、命题“”的否定是_ ____.
2、已知点,且该点在三个坐标平面平面,平面,平面上的射影的坐标依次为,和,则的值为 .
3、如图所示的等腰直角三角形表示一个水平放置的平面图形的
直观图,则这个平面图形的面积是 _ ____.
4、设为不重合的三个平面,表示直线,下列叙述正确的序号是 _ ___.
① 若,则PQ;
②若,,则且;
③ 若∥且∥,则∥;
④ 若,则。
第8题图
5、设A是C的充分必要条件,B是C的充分条件,D是C的必要条件,D是B的充分条件,那么A是B的__ _____条件
6、一个长方体的各顶点均在同一球的球面上,且一个顶点上的三条棱的长分别为1,2,3,则此球的表面积为_ ____.
7、已知=(1,-1,3),=(-1,4,-2),=(7,5,λ),若、、三向量共面,则实数λ等于 .
8、如右上图,正方体,点M是的中点,点O是底面的中心,
P是上的任意一点,则直线BM与OP所成的角大小为 __
9、个圆台的体积是,它的下底面积是上底面积的9倍,则截得这个圆台的圆锥的体积是 _ ____.
10、在正方体ABCD-A1B1C1D1中,给出下面三个判断:
①;②;③与的夹角为600; 其中正确的序号是 .
11、如图有一根高为,底面半径为的圆柱形铁管,用一段铁丝在铁管上缠绕2圈,并使铁丝的两个端点落在圆柱的同一母线的两端,则铁丝的最短长度为 (结果用表示)
12、已知正三棱锥直观图、主视图如图所示,其中主视图中,,则这个正三棱锥的左视图的面积为 .
13、设x、y、z是空间不同的直线或不同的平面,且直线不在平面内,在下列几个条件中,能保证“若x⊥z且y⊥z,则x∥y”为真命题的有 。
①x为直线,y、z是平面; ②x、y、z均为平面;
③x、y为直线,z为平面; ④x、y为平面,z为直线
14、已知,,,点Q在直线OP上运动,则当取得最小值时,点Q的坐标为 _ ____.
二.解答题:本大题共6小题,共90分.解答应写出文字说明,证明过程或演算步骤.
15、(本小题满分14分)如图,在正方体ABCD-A1B1C1D1中,点E、F分别是AA1、CC1的中点,(1) 求证:点D1、E、F、B共面.(2)连结D1E并延长交DA的延长线于M,连结D1F并延长交DC的延长线于N,求证:M、B、N共线
16、(本小题满分14分)在正方体中,分别是,CD的中点,
(1)求证:平面ADE; (2)求的夹角
17、(本小题满分15分)
某高速公路收费站入口处的安全标识墩直观图、主(正)视图和俯视图如图所示。墩的上半部分是正四棱锥,下半部分是长方体。
(1)请画出该安全标识墩的侧(左)视图;(2)求该安全标识墩的体积;
(3)该安全标识墩的表面(不包括下底面)由铁皮制成,问制造一个这样的安全标识墩至少需要多少平方厘米的铁皮?
18、(本小题满分15分)
如图,在三棱柱中,,分别为线段的中点,求证:(1)面;(2)平面;(3)试在上找一点,使平面∥平面,并证明你的结论;
19、(本小题满分16分)
如图,正四棱柱中,底面边长为2,侧棱长为3,E为BC的中点,FG分别为、上的点,且CF=2GD=2.求:
(1)DC与面EFG所成的角正弦值;
(2)求二面角E-GF-C的余弦值;
(3)在直线上是否存在点P,使得DP//面EFG?,若存在,找出点P的位置,若不存在,试说明理由。
20.(本题满分16分)
三个全等的等边三角形拼成如图l所示的等腰梯形ABCD,AD∥BC.将△ABE沿AE折起,使平面平面(如图2),连结BC、BD,点F、P分别是CD、BC的中点.
(1)若M是AE中点,求证:AE⊥平面BMD;(4分) ’
(2)求证:平面PEF⊥平面AECD;(6分)
(3)判断DE能否垂直于平面ABC?并说明理由.(4分)
如皋市四校09-10学年高二上学期期中联考试题
高二数学参考答案及评分标准
填空题
1. 2. 0 3. 4. _① 、 ② 、③ 5. _充要
6. 7. 25 8. 9. 54 10. ① 、 ② 11. 5 12. 13. ①、③、④ 14.
二、解答题
15.(本题满分14分)
证明:(1)取中点G,因为E、G分别为AA1,B1B的中点,所以四边形AEGB1为平行四边形, ,又,所以,即四边形EGC1D1为平行四边形,所以,又四边形BGFC1为平行四边形,C1G∥BF,所以BF∥D1E,所以点D1、E、F、B共面……………7分
(2)由(1)得D1、E、F、B共面,设平面D1EFB平面ABCD=,则B,
又M= D1EDA,所以M平面D1EFB,且M平面ABCD,所以M,同理N
所以M、B、N都在直线上,即M、B、N共线。……………14分
16.解:建立如图所示的直角坐标系……………………………………………………1分
(1)不妨设正方体的棱长为1,
则D(0,0,0),A(1,0,0),(0,0,1),
E(1,1,),F(0,,0),
则=(0,,-1),=(1,0,0),
=(0,1,),
则=0,
=0,
,.
平面ADE. ………………………………………7分
(2)(1,1,1),C(0,1,0),
故=(1,0,1),=(-1,-,-),…………………9分
=-1+0-=-,
,,
则cos. ……… ………13分
…………………………………………………14分
17(本题满分15分).
(1)侧视图同正视图,如下图所示. ………………4分
(2)该安全标识墩的体积为:
…………………………………………………9分
(3)由题意知正四棱锥的斜高为…………………………………………………12分
所以表面积
答:略…………………………………………………15分
18.(本题满分15分)
(1),
,
面;………………4分
(2)
………………………………………………9分
(3)G为中点………………………………………………10分
………………………………………………………………………15分
19. (本题满16分)
解:(1)如图,以D为原点建立空间直角坐标系
则E(1,2,0),F(0,2,2),G(0,0,1)
∴=(-1,0,2),=(0,-2,-1),
设=(x,y,z)为面EFG的法向量,则
=0,=0,x=2z,z=-2y,取y=1,
得=(-4,1,-2) …………………………4分
=(0,2,0),设DC与面EFG所成的角为θ,
则,=…………………………7分
(2)设二面角E-GF-C的平面角为
易知=(2,0,0)为面的法向量…………………………………8分
二面角E-GF-C的余弦值为………………………………………………11分
(3)存在点P,在B点下方且BP=3, …………………………………13分
假设存在点P(2,2,x)使得DP//面EFG
由 =0得 x=-3
所以:存在点P,在B点下方且BP=3,此时P(2,2,-3)
=(2,2,-3),∴=0,∴DP//面EFG ……………………………………16分
20. (本题满分16分)
证明:(1)取中点,连接.
与都是等边三角形
平面
平面………………………………………………4分
(2)证明:
…………………………………………………………………………………………10分
(3)与平面不垂直.………………………………………………11分
证明:假设平面, 则
平面
,平面 平面
,这与矛盾
与平面不垂直.
…………………………………………………………………………………16分
同课章节目录
