数学四年级下冀教版3.5乘法运算律课件
图片预览




文档简介
(共26张PPT)
3 乘法
3.5 乘法运算律
学习目标
理解并掌握乘法的交换律和结合律
能够应用乘法的运算定律解决相关的实际问题
情景导入
用计算器计算上面的算式,在方框内填上适当的运算符号。
645×32 32×645
203×46 46×203
180×53 53×180
探索新知
在一个乘法算式里面,乘数和被乘数都叫做因数。通过上面计算两边的算式,你发现了什么呢?
上面左右两个乘法算式的积相同
这个和前面学习的加法交换律差不多,上面的两个算式交换因数的位置,乘积不变。
探索新知
不仅仅上面这几个乘法算式有这个性质,任何两个数相乘,交换因数的位置,积都不变,乘法的这个性质就叫做乘法交换律。乘法交换律和加法交换律比较相似,简化可以说成:交换位置,积不变。
探索新知
我用x×y=y×x
用字母表示一下乘法的交换律,自己试一试。
我用a×b=b×a
情景导入
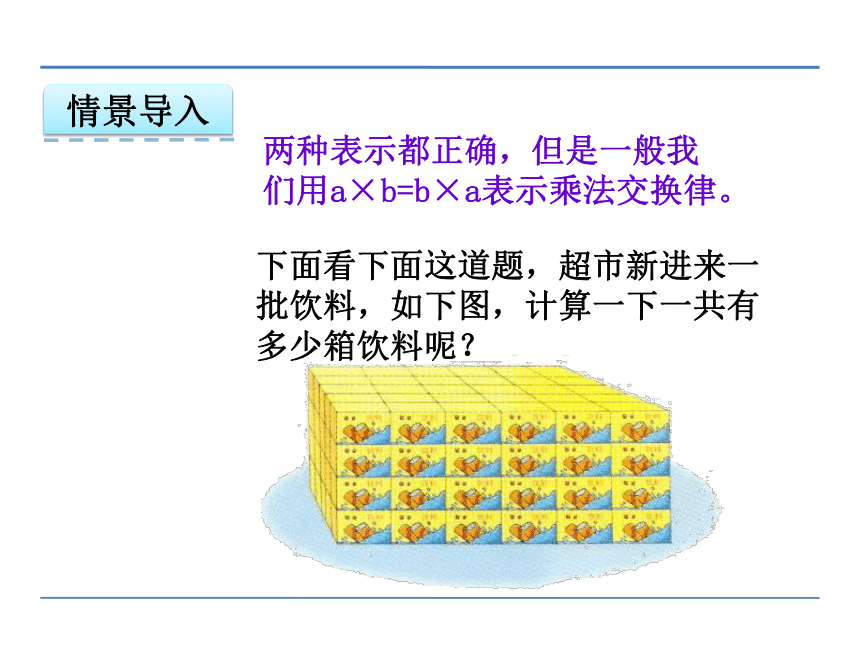
两种表示都正确,但是一般我们用a×b=b×a表示乘法交换律。
下面看下面这道题,超市新进来一批饮料,如下图,计算一下一共有多少箱饮料呢?
探索新知
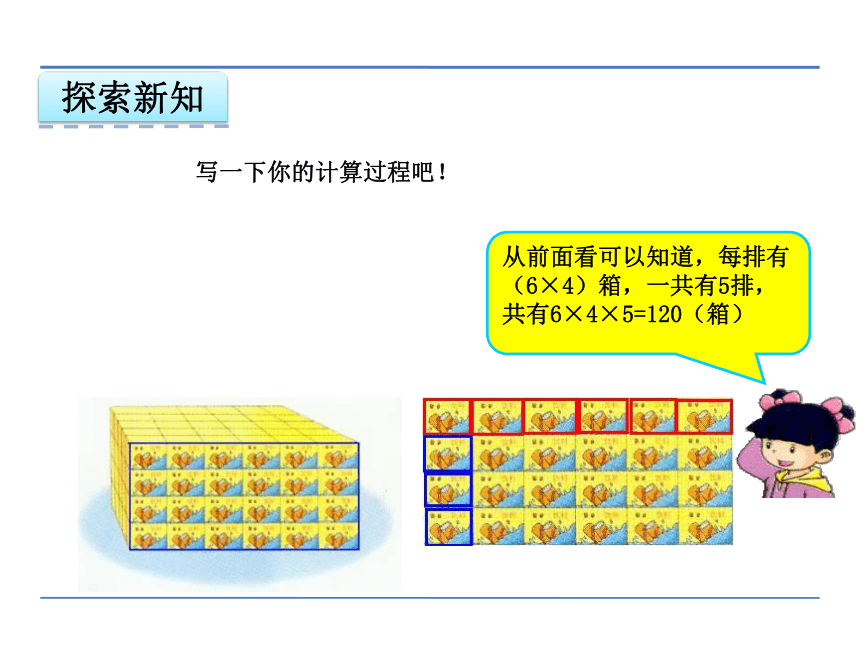
从前面看可以知道,每排有(6×4)箱,一共有5排,共有6×4×5=120(箱)
写一下你的计算过程吧!
探索新知
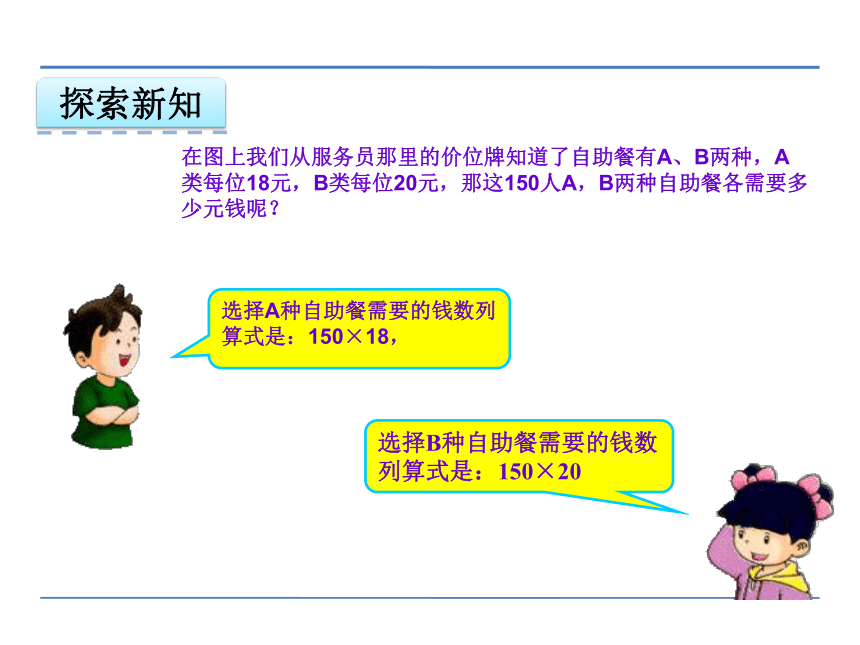
在图上我们从服务员那里的价位牌知道了自助餐有A、B两种,A类每位18元,B类每位20元,那这150人A,B两种自助餐各需要多少元钱呢?
选择A种自助餐需要的钱数列算式是:150×18,
选择B种自助餐需要的钱数列算式是:150×20
探索新知
我从侧面看的,每列有(4×5)箱,一共有6列,共有4×5×6=120(箱)
探索新知
我从上面看的,每层有(6×5)箱,有4层,共有6×5×4=120(箱)
探索新知
这三种方法的结算结果都是120,结果相同,都正确,也就是说:6×4×5=6×5×4=6×(4×5)
6×4×5=6×5×4=6×(4×5),它们是三个数相乘,结果相同,不同的只是它们的位置变了一下,计算顺序也变了一下。我们再来看下面这两组算式,看是不是有同样的规律,
(1) 36×4×25
36×(4×25)
(2) 5×28×6
5×6×28
探索新知
第一组我计算的结果都是3600,所以它们的关系是:
36×4×25=36×(4×25)
第二组我计算的结果都是840,所以它们的关系是:
5×28×6=5×6×28
探索新知
对了,经我们检验,这个规律是成立的,它就叫做乘法的结合律,指的就是在含有三个或三个以上的因数的乘法算式里,先结合任意两个因数的积,这个算式的积不变。
用字母表示乘法结合律就是:a×b×c= a×(b×c),我们一般都用这种形式来表示,但是乘法的结合律不仅仅指的是先结合后面的两个因数,它包含的意思的是可以结合任意两个因数。
一共有多少名同学参加了这次植树活动?
典题精讲
(4+2)×25
=6×25
=150
4×25+2×25
=100+50
=150
你还有其他的算法吗?
这两种算法有什么相同点和不同点?
典题精讲
用字母表示乘法分配律:(a+b)×c= a×c+b×c
两个数的和与一个数相乘,可以先把它们与这个数分别相乘,再相加。这叫做乘法分配律。
学以致用
现在看下面的这两道题,运用这个规律,看怎样计算更简便
50×26×4
25×37×20
学以致用
50×26×4
=50×4×26
=200×26
=5200
25×37×20
=25×20×37
=500×37
=18500
情景导入
我们学习了两条乘法运算定律了,接着我们看下面的应用题。下面是亮亮家客厅的两扇屏风,这个屏风上面有很多玻璃,计算一下上面究竟有多少玻璃呢?看下图:
探索新知
12×5+9×5
=60+45
=105
一共有两扇屏风,可以先算一扇,再算另一扇,然后把它们的得数加起来就是总数。列综合算式就是:
探索新知
我是先算的最上面一层有多少块玻璃,第一块屏风的第一层有12块,第二块第一层有9块,然后是一共5层,用乘法就能算出总数,列综合算式就是:
(12+9)×5
=21×5
=105
探索新知
他们两个的算法都很正确,他们的综合算式的结果是相等的,列在一起就是:
12×5+9×5=(12+9)×5
这个规律就是乘法的第三条运算定律,叫做乘法分配律,乘法分配律指的是两个数相加的和与第三个数相乘,可以先把每一个数与第三个数相乘,再把乘得的积相加。用字母表示就是:(a+b)×c=a×c+b×c
103×12
=(100+3)×12
=100×12+3×12
=1200+36
=1236
20×55
=20×(50+5)
=20×50+20×5
=1000+100
=1100
5. 用乘法分配律计算下面各题。
学以致用
学以致用
乘法的分配律可以使我们的计算更简便,我们看下面的算式:
38×53+53×62
如果我们按计算顺序一步一步往下计算会很麻烦,如果用乘法分配律的话,你会发现非常简单的:
38×53+53×62
=(38+62)×53
=100×53
=5300
利用乘法分配律进行简便运算一般都是进行“凑整”,凑成整百,整十,整千的来计算,还要注意多利用,25×4=100,125×8=1000这样的算式。
课堂小结
1、两个因数相乘,交换因数的位置,积不变,这就叫做乘法交换律。
a×b=b×a
2、三个数相乘,先乘前两个数或先乘后两个数,积不变,这就叫做乘法结合律。
a×b×c= a×(b×c)
乘法分配律指的是两个数相加的和与第三个数相乘,可以先把每一个数与第三个数相乘,再把乘得的积相加。
(a+b)×c=a×c+b×c
3 乘法
3.5 乘法运算律
学习目标
理解并掌握乘法的交换律和结合律
能够应用乘法的运算定律解决相关的实际问题
情景导入
用计算器计算上面的算式,在方框内填上适当的运算符号。
645×32 32×645
203×46 46×203
180×53 53×180
探索新知
在一个乘法算式里面,乘数和被乘数都叫做因数。通过上面计算两边的算式,你发现了什么呢?
上面左右两个乘法算式的积相同
这个和前面学习的加法交换律差不多,上面的两个算式交换因数的位置,乘积不变。
探索新知
不仅仅上面这几个乘法算式有这个性质,任何两个数相乘,交换因数的位置,积都不变,乘法的这个性质就叫做乘法交换律。乘法交换律和加法交换律比较相似,简化可以说成:交换位置,积不变。
探索新知
我用x×y=y×x
用字母表示一下乘法的交换律,自己试一试。
我用a×b=b×a
情景导入
两种表示都正确,但是一般我们用a×b=b×a表示乘法交换律。
下面看下面这道题,超市新进来一批饮料,如下图,计算一下一共有多少箱饮料呢?
探索新知
从前面看可以知道,每排有(6×4)箱,一共有5排,共有6×4×5=120(箱)
写一下你的计算过程吧!
探索新知
在图上我们从服务员那里的价位牌知道了自助餐有A、B两种,A类每位18元,B类每位20元,那这150人A,B两种自助餐各需要多少元钱呢?
选择A种自助餐需要的钱数列算式是:150×18,
选择B种自助餐需要的钱数列算式是:150×20
探索新知
我从侧面看的,每列有(4×5)箱,一共有6列,共有4×5×6=120(箱)
探索新知
我从上面看的,每层有(6×5)箱,有4层,共有6×5×4=120(箱)
探索新知
这三种方法的结算结果都是120,结果相同,都正确,也就是说:6×4×5=6×5×4=6×(4×5)
6×4×5=6×5×4=6×(4×5),它们是三个数相乘,结果相同,不同的只是它们的位置变了一下,计算顺序也变了一下。我们再来看下面这两组算式,看是不是有同样的规律,
(1) 36×4×25
36×(4×25)
(2) 5×28×6
5×6×28
探索新知
第一组我计算的结果都是3600,所以它们的关系是:
36×4×25=36×(4×25)
第二组我计算的结果都是840,所以它们的关系是:
5×28×6=5×6×28
探索新知
对了,经我们检验,这个规律是成立的,它就叫做乘法的结合律,指的就是在含有三个或三个以上的因数的乘法算式里,先结合任意两个因数的积,这个算式的积不变。
用字母表示乘法结合律就是:a×b×c= a×(b×c),我们一般都用这种形式来表示,但是乘法的结合律不仅仅指的是先结合后面的两个因数,它包含的意思的是可以结合任意两个因数。
一共有多少名同学参加了这次植树活动?
典题精讲
(4+2)×25
=6×25
=150
4×25+2×25
=100+50
=150
你还有其他的算法吗?
这两种算法有什么相同点和不同点?
典题精讲
用字母表示乘法分配律:(a+b)×c= a×c+b×c
两个数的和与一个数相乘,可以先把它们与这个数分别相乘,再相加。这叫做乘法分配律。
学以致用
现在看下面的这两道题,运用这个规律,看怎样计算更简便
50×26×4
25×37×20
学以致用
50×26×4
=50×4×26
=200×26
=5200
25×37×20
=25×20×37
=500×37
=18500
情景导入
我们学习了两条乘法运算定律了,接着我们看下面的应用题。下面是亮亮家客厅的两扇屏风,这个屏风上面有很多玻璃,计算一下上面究竟有多少玻璃呢?看下图:
探索新知
12×5+9×5
=60+45
=105
一共有两扇屏风,可以先算一扇,再算另一扇,然后把它们的得数加起来就是总数。列综合算式就是:
探索新知
我是先算的最上面一层有多少块玻璃,第一块屏风的第一层有12块,第二块第一层有9块,然后是一共5层,用乘法就能算出总数,列综合算式就是:
(12+9)×5
=21×5
=105
探索新知
他们两个的算法都很正确,他们的综合算式的结果是相等的,列在一起就是:
12×5+9×5=(12+9)×5
这个规律就是乘法的第三条运算定律,叫做乘法分配律,乘法分配律指的是两个数相加的和与第三个数相乘,可以先把每一个数与第三个数相乘,再把乘得的积相加。用字母表示就是:(a+b)×c=a×c+b×c
103×12
=(100+3)×12
=100×12+3×12
=1200+36
=1236
20×55
=20×(50+5)
=20×50+20×5
=1000+100
=1100
5. 用乘法分配律计算下面各题。
学以致用
学以致用
乘法的分配律可以使我们的计算更简便,我们看下面的算式:
38×53+53×62
如果我们按计算顺序一步一步往下计算会很麻烦,如果用乘法分配律的话,你会发现非常简单的:
38×53+53×62
=(38+62)×53
=100×53
=5300
利用乘法分配律进行简便运算一般都是进行“凑整”,凑成整百,整十,整千的来计算,还要注意多利用,25×4=100,125×8=1000这样的算式。
课堂小结
1、两个因数相乘,交换因数的位置,积不变,这就叫做乘法交换律。
a×b=b×a
2、三个数相乘,先乘前两个数或先乘后两个数,积不变,这就叫做乘法结合律。
a×b×c= a×(b×c)
乘法分配律指的是两个数相加的和与第三个数相乘,可以先把每一个数与第三个数相乘,再把乘得的积相加。
(a+b)×c=a×c+b×c
