第一章 三角形的证明 单元测试A卷基础训练(含详解) 2024-2025学年北师大版数学八年级下册
文档属性
| 名称 | 第一章 三角形的证明 单元测试A卷基础训练(含详解) 2024-2025学年北师大版数学八年级下册 |  | |
| 格式 | docx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-10 20:23:13 | ||
图片预览

文档简介
第一章 三角形的证明 单元测试A卷基础训练
【满分:120】
一、选择题:(本大题共10小题,每小题4分,共40分,给出的四个选项中,只有一项是符合题目要求的)
1.牛顿曾说过:“反证法是数学家最精良的武器之一.”那么我们用反证法证明:“在一个三角形中,至少有一个内角小于或等于时,第一步先假设( )
A.三角形中有一个内角小于 B.三角形中有一个内角大于
C.三角形中每个内角都大于 D.三角形中没有一个内角小于
2.如图,已知,,若用判定和全等,则需要添加的条件是( )
A. B. C. D.
3.下列条件中,可以判定是等腰三角形的是( )
A. B.
C. D.三个角的度数之比是2:2:1
4.“三等分角”大约是在公元前五世纪由古希腊人提出来的.借助如图所示的“三等分角仪”能三等分任一角.这个三等分角仪由两根有槽的棒,组成,两根棒在O点相连并可绕O转动,C点固定,,点D,E可在槽中滑动,若,则的度数是( )
A.60° B.65° C.75° D.80°
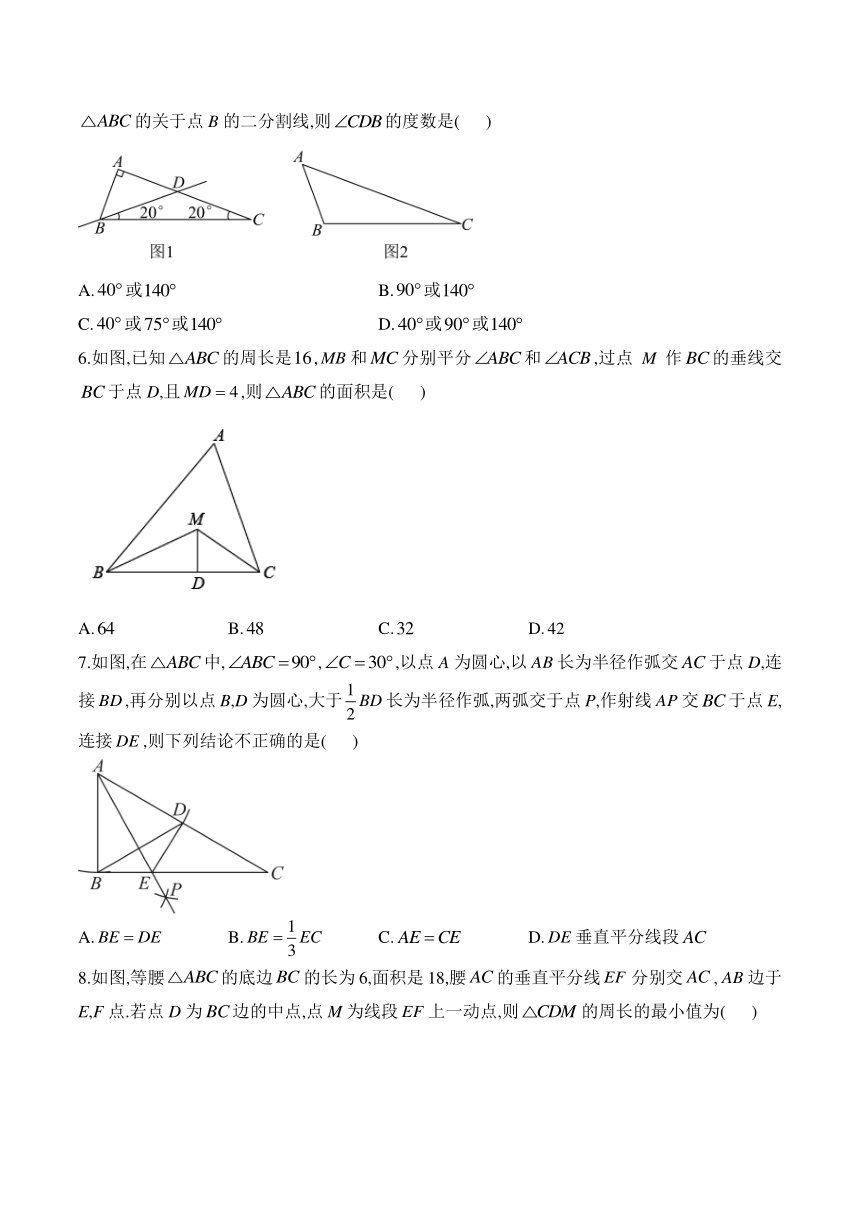
5.已知中,如果过顶点B的一条直线把这个三角形分割成两个三角形,其中一个为等腰三角形,另一个为直角三角形,则称这条直线为的关于点B的二分割线.如图1,中,显然直线是的关于点B的二分割线.在图2的中,,若直线是的关于点B的二分割线,则的度数是( )
A.或 B.或
C.或或 D.或或
6.如图,已知的周长是,和分别平分和,过点M作的垂线交于点D,且,则的面积是( )
A. B. C. D.
7.如图,在中,,,以点A为圆心,以长为半径作弧交于点D,连接,再分别以点B,D为圆心,大于长为半径作弧,两弧交于点P,作射线交于点E,连接,则下列结论不正确的是( )
A. B. C. D.垂直平分线段
8.如图,等腰的底边的长为6,面积是18,腰的垂直平分线分别交,边于E,F点.若点D为边的中点,点M为线段上一动点,则的周长的最小值为( )
A.6 B.8 C.9 D.10
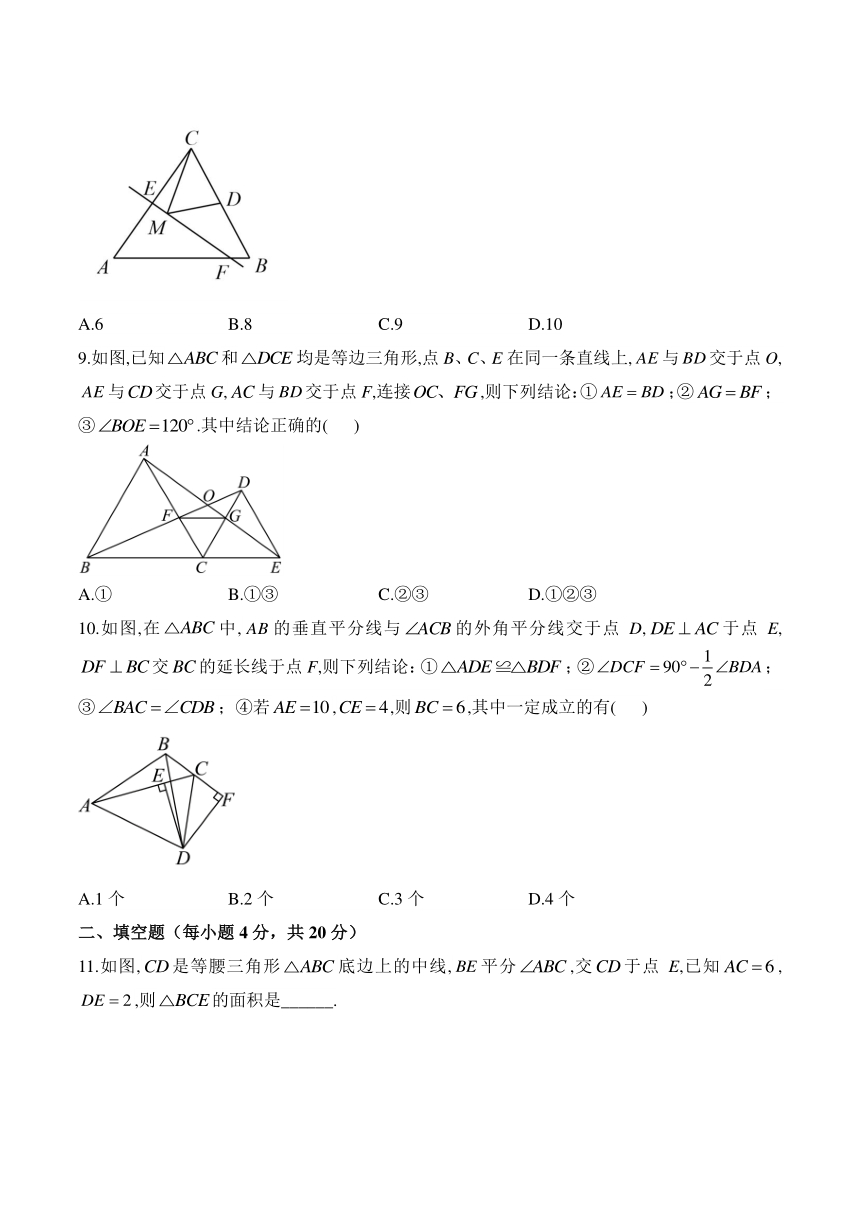
9.如图,已知和均是等边三角形,点B、C、E在同一条直线上,与交于点O,与交于点G,与交于点F,连接,则下列结论:①;②;③.其中结论正确的( )
A.① B.①③ C.②③ D.①②③
10.如图,在中,的垂直平分线与的外角平分线交于点D,于点E,交的延长线于点F,则下列结论:①;②;③;④若,,则,其中一定成立的有( )
A.1个 B.2个 C.3个 D.4个
二、填空题(每小题4分,共20分)
11.如图,是等腰三角形底边上的中线,平分,交于点E,已知,,则的面积是______.
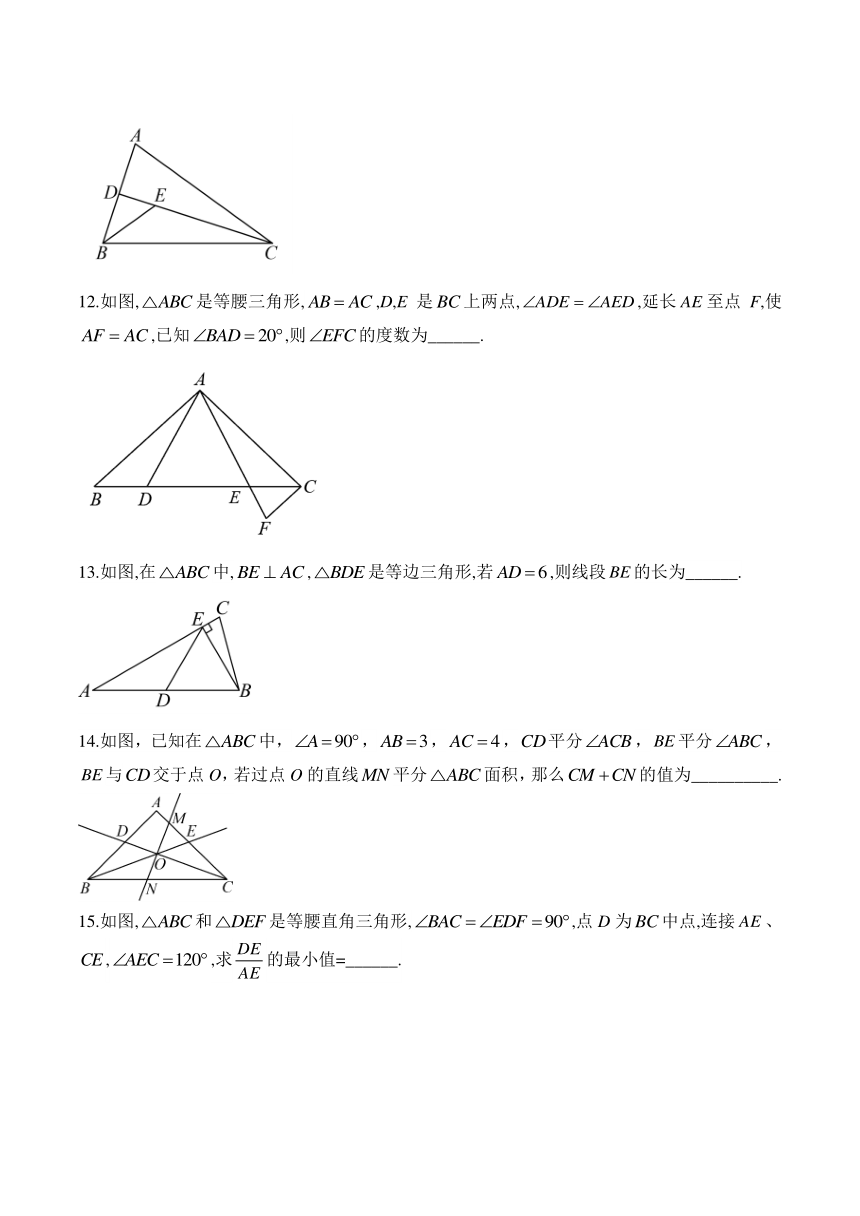
12.如图,是等腰三角形,,D,E是上两点,,延长至点F,使,已知,则的度数为______.
13.如图,在中,,是等边三角形,若,则线段的长为______.
14.如图,已知在中,,,,平分,平分,与交于点O,若过点O的直线平分面积,那么的值为__________.
15.如图,和是等腰直角三角形,,点D为中点,连接、,,求的最小值=______.
三、解答题(本大题共6小题,共计60分,解答题应写出演算步骤或证明过程)
16.(8分)用反证法证明:
(1)已知:,求证:a必为负数.
(2)求证:形如的整数k(n为整数)不能化为两个整数的平方和.
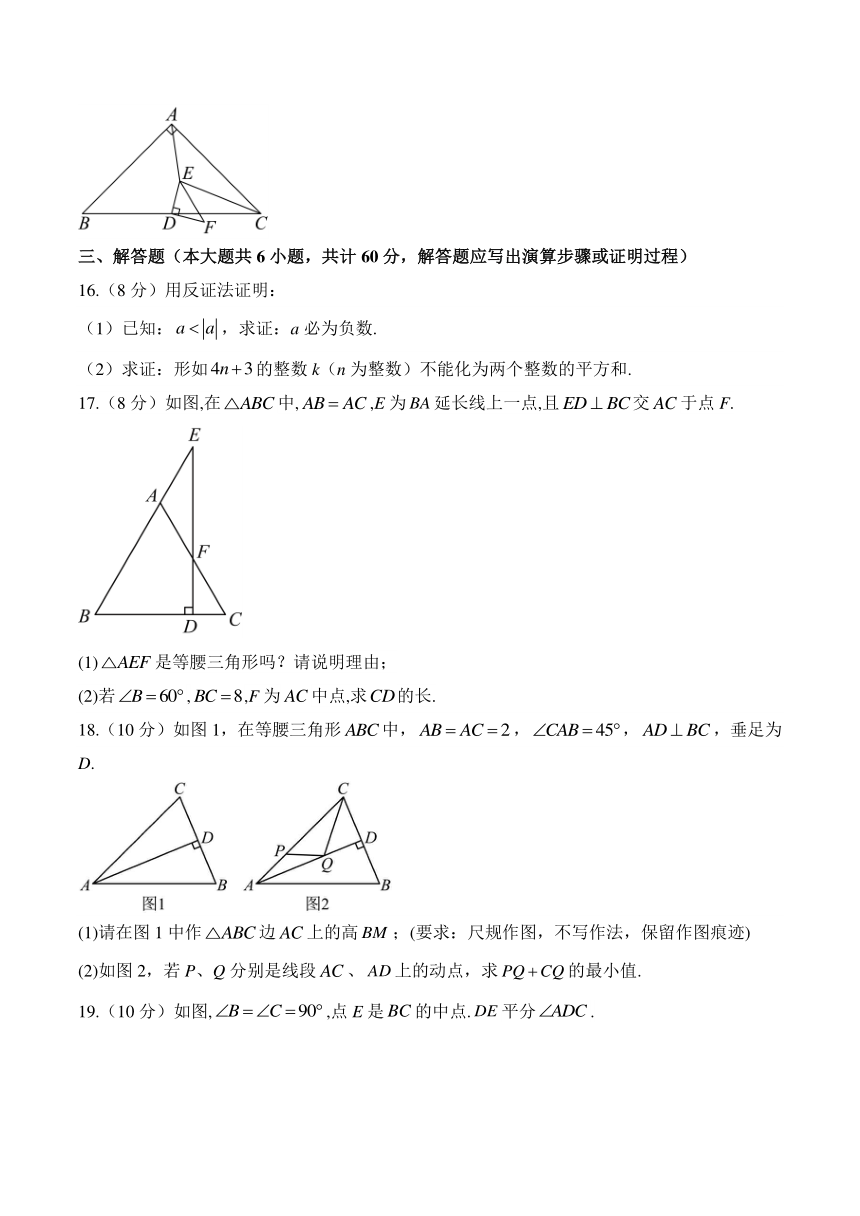
17.(8分)如图,在中,,E为延长线上一点,且交于点F.
(1)是等腰三角形吗?请说明理由;
(2)若,,F为中点,求的长.
18.(10分)如图1,在等腰三角形中,,,,垂足为D.
(1)请在图1中作边上的高;(要求:尺规作图,不写作法,保留作图痕迹)
(2)如图2,若P、Q分别是线段、上的动点,求的最小值.
19.(10分)如图,,点E是的中点.平分.
(1)求证:是的平分线;
(2)已知,,求四边形的面积.
20.(12分)问题情景:如图直角中,,,,求的长?
解题思路:把的角转化成特殊角度,再利用特殊角度进行边之间的换算.
解决方案:方法一:延长至B,使得,过作,交于点,根据角平分线的性质定理和等腰直角三角形边的关系,可得
方法二:作的中垂线交于点F,连接,根据中垂线的性质定理和等腰直角三角形边的关务,设,,,,得,,则.
其他方法……
迁移应用解决新问题:如图直角中,,,,求的长,写出你的解答过程.
21.(12分)定义:如果一个三角形一边的平方与另一边上高的平方之和等于第三边的平方,则称这个三角形为“牵手三角形”,这条边与第三边的交点称为“牵手顶点”.例如图1,在中,,是边上的高,若,则为“牵手三角形”,点B为“牵手顶点”.
(1)等边三角形______“牵手三角形”(填写“是”或者“不是”);
(2)如图2,已知为“牵手三角形”,其中点A为“牵手顶点”,,是边上的高.在不添加其他线段和字母的情况下,找出图中一组相等的线段,并说明理由;
(3)运用(2)中的结论解决下列问题:
①已知为“牵手三角形”,其中点C为“牵手顶点”且,是边上的高.若,,则的长是______;
②如图3,为“牵手三角形”,其中,A为“牵手顶点”,是边上的高,,若,.求证:为等腰三角形.
答案以及解析
1.答案:C
解析:用反证法证明:在一个三角形中,至少有一个内角小于或等于时,
第一步先假设三角形中每个内角都大于,
故选:C.
2.答案:A
解析:,,
,
A.,符合两直角三角形全等的判定定理,故该选项符合题意;
B.,,不是两直角三角形全等的判定定理,故该选项不符合题意;
C.,不符合两直角三角形全等的判定定理,故该选项不符合题意;
D.,,不是两直角三角形全等的判定定理,故该选项不符合题意;
故选:A.
3.答案:D
解析:对于选项A,
故选项A不能判定为等腰三角形;
对于选项B,
可设,
解得:,
故选项B不能判定为等腰三角形;
对于选项C,
解得:,
此时不能确定和的度数,无法判定的形状,
故选项C不能判定为等腰三角形;
对于选项D,
三个角的度数之比是2:2:1
不妨假设,
可设,
解得:,
故选项D可以判定为等腰三角形.
故选:D
4.答案:D
解析:∵,
∴,,
设,
∴,
∴,
∵,
∴,
即,
解得:,
.
故答案为D.
5.答案:D
解析:在中,,若直线是的关于点B的二分割线,
∴①如图所示,当,,即是等腰三角形,是直角三角形,满足条件,
∴;
②如图所示,当,,即是直角三角形,是等腰三角形,满足条件,
∴,
∴;
③如图所示,当,,即是等腰三角形,是直角三角形,满足条件,
∴,
∵是的外角,
∴,
综上所述,的度数是或或,
故选:D.
6.答案:C
解析:连接,过M作于E,于F,
和分别平分和,,,
,,
的周长是,
,
的面积
,
故选:C.
7.答案:B
解析:由作图可知:,,
∴垂直平分,
又∵点E在上,
∴,故A正确,但不合题意;
∵,,
∴,又
∴,又
∴
∵垂直平分,
∴是等腰三角形,
∴
又,
∴,
∴,故C正确,但不符合题意.
由可知,垂直平分线段,
故D正确,但不符合题意.
由点A在线段的垂直平分线上知,
,
∴.
故B不正确,但符合题意.
故选:B.
8.答案:C
解析:如图,连接,.
∵是等腰三角形,点D是边的中点,
∴,
∴,解得.
∵是线段的垂直平分线,
∴点A关于直线的对称点为点C,,
∴,
∴的长为的最小值,
∴的周长.
故选:C.
9.答案:D
解析:∵和均是等边三角形,
∴,,
∴
∴
在和中
∴,
∴,∴①正确;
∴
∵
∴
∴在和中
∴,
∴,∴②正确;
∵
∴
∵
∴
∴,
∴③正确.故选D.
10.答案:D
解析:①∵是的外角平分线,,,
∴
∵D在的垂直平分线上,
∴,
∴,
故①正确;
在上截取,
∵
∴,,
∵,,
∴,
∵,
∴,,
,,
,
,
,
,
故④正确.
∵,
,
,,
∴,
∵,
∴,
∴;
故③正确;
∵,,
∴,,
,
∴,
,
,
∴,
即,故②正确;故选D.
11.答案:6
解析:作于F,
∵,是等腰三角形底边上的中线,
∴,
∵平分,,,
∴,
∴的面积,
故答案为:6.
12.答案:/度
解析:∵
∴,
又∵,
∴,
∴,
∴,
∵,
∴,
故答案为:.
13.答案:6
解析:∵是等边三角形,
,,
,
,
,
,
,
,
,
,
,
故答案为:6.
14.答案:6
解析:如图所示,过点O作,,垂足分别为H、G、P,连接,
∵平分,平分,
∴,
在中,,,,
∴,
∵,
∴,
∴,
∴,
∵过点O的直线平分面积,
∴,
∴,
∴,
∴,
故答案为:6.
15.答案:
解析:连接、,
∵点D为中点,是等腰直角三角形,
∴,
∵是等腰直角三角形,
∴,,
∴,
∴,
∴,,
∵,
∴,
∵,
∴,
∴,
∴当时,最小,此时
∴的最小值为,
故答案为:.
16.答案:(1)见解析
(2)见解析
解析:(1)证明:假设,则,这与已知相矛盾,
假设不成立,
a必为负数;
(2)证明:假设的整数部分k能化成两个整数的平方和,不妨设这两个整数为,,
则,
,
假设不成立,
的整数k不能化为两个整数的平方和.
17.答案:(1)是等腰三角形,见解析
(2)2
解析:(1)是等腰三角形.
理由:因为,
所以.
因为,
所以,
所以,,
所以.
因为,
所以,
所以,即为等腰三角形;
(2)因为,,
所以是等边三角形,
所以,.
因为,
所以.
因为F是的中点,
所以.
在中,,
所以.
18.答案:(1)作图见解析
(2)
解析:(1)如图,线段为所求作的图形;
(2)如图,
∵,,
∴为的垂直平分线,
∴,
∴,
所以当B,Q,P三点共线且时
此时的值最小,
∵,,
∴为等于直角三角形,,
∴,
即,
解得,
∴的最小值为.
19.答案:(1)见解析
(2)12
解析:(1)证明:过点E作于点F,如图所示:
∵,
∴,
∵是的平分线,
∴,
∵点E是的中点,
∴,
∴,
∴是的平分线;
(2)∵,,
∴,
∴,,
∵,,
∴,
∴,,
∴,
即,
∵,
∴.
20.答案:,见解析
解析:方法一:延长至B,使得,过作,交于点E.
∵,,,
∴.
∵,,
∴,.
∴,,
∴
∵,,
∴.
∴.
设,则:,,
∴,
∴,
∴.
方法二:作的中垂线交于点F,连接.
∵的中垂线交于点F,
∴.
∵,
∴.
∴.
∴.
∴,,
设,则,,
∴,
解得:.
∴.
21.答案:(1)不是
(2),理由见解析
(3)①8;②见解析
解析:(1)∵等边三角形的三边相等,
∴等边三角形一边的平方与另一边上高的平方之和大于第三边的平方,
∴等边三角形不是“牵手三角形”;
故答案为:不是
(2),理由如下:
∵为“牵手三角形”,是边上的高,
∴,
在中,,
∴,
∴;
(3)①如图,
由(2)得:,
在中,,
∴,
∴,
∴;
故答案为:8
②证明:由(2)得:,
∵,
∴和、均为直角三角形,
在和中,
∵,,
∴,
∴,,
∴,
∵,
∴,
即,
如图,延长交于点F,
在和中,
∵,,,
∴,
∴,
∵,
∴,
∴,
∴,∴为等腰三角形.
【满分:120】
一、选择题:(本大题共10小题,每小题4分,共40分,给出的四个选项中,只有一项是符合题目要求的)
1.牛顿曾说过:“反证法是数学家最精良的武器之一.”那么我们用反证法证明:“在一个三角形中,至少有一个内角小于或等于时,第一步先假设( )
A.三角形中有一个内角小于 B.三角形中有一个内角大于
C.三角形中每个内角都大于 D.三角形中没有一个内角小于
2.如图,已知,,若用判定和全等,则需要添加的条件是( )
A. B. C. D.
3.下列条件中,可以判定是等腰三角形的是( )
A. B.
C. D.三个角的度数之比是2:2:1
4.“三等分角”大约是在公元前五世纪由古希腊人提出来的.借助如图所示的“三等分角仪”能三等分任一角.这个三等分角仪由两根有槽的棒,组成,两根棒在O点相连并可绕O转动,C点固定,,点D,E可在槽中滑动,若,则的度数是( )
A.60° B.65° C.75° D.80°
5.已知中,如果过顶点B的一条直线把这个三角形分割成两个三角形,其中一个为等腰三角形,另一个为直角三角形,则称这条直线为的关于点B的二分割线.如图1,中,显然直线是的关于点B的二分割线.在图2的中,,若直线是的关于点B的二分割线,则的度数是( )
A.或 B.或
C.或或 D.或或
6.如图,已知的周长是,和分别平分和,过点M作的垂线交于点D,且,则的面积是( )
A. B. C. D.
7.如图,在中,,,以点A为圆心,以长为半径作弧交于点D,连接,再分别以点B,D为圆心,大于长为半径作弧,两弧交于点P,作射线交于点E,连接,则下列结论不正确的是( )
A. B. C. D.垂直平分线段
8.如图,等腰的底边的长为6,面积是18,腰的垂直平分线分别交,边于E,F点.若点D为边的中点,点M为线段上一动点,则的周长的最小值为( )
A.6 B.8 C.9 D.10
9.如图,已知和均是等边三角形,点B、C、E在同一条直线上,与交于点O,与交于点G,与交于点F,连接,则下列结论:①;②;③.其中结论正确的( )
A.① B.①③ C.②③ D.①②③
10.如图,在中,的垂直平分线与的外角平分线交于点D,于点E,交的延长线于点F,则下列结论:①;②;③;④若,,则,其中一定成立的有( )
A.1个 B.2个 C.3个 D.4个
二、填空题(每小题4分,共20分)
11.如图,是等腰三角形底边上的中线,平分,交于点E,已知,,则的面积是______.
12.如图,是等腰三角形,,D,E是上两点,,延长至点F,使,已知,则的度数为______.
13.如图,在中,,是等边三角形,若,则线段的长为______.
14.如图,已知在中,,,,平分,平分,与交于点O,若过点O的直线平分面积,那么的值为__________.
15.如图,和是等腰直角三角形,,点D为中点,连接、,,求的最小值=______.
三、解答题(本大题共6小题,共计60分,解答题应写出演算步骤或证明过程)
16.(8分)用反证法证明:
(1)已知:,求证:a必为负数.
(2)求证:形如的整数k(n为整数)不能化为两个整数的平方和.
17.(8分)如图,在中,,E为延长线上一点,且交于点F.
(1)是等腰三角形吗?请说明理由;
(2)若,,F为中点,求的长.
18.(10分)如图1,在等腰三角形中,,,,垂足为D.
(1)请在图1中作边上的高;(要求:尺规作图,不写作法,保留作图痕迹)
(2)如图2,若P、Q分别是线段、上的动点,求的最小值.
19.(10分)如图,,点E是的中点.平分.
(1)求证:是的平分线;
(2)已知,,求四边形的面积.
20.(12分)问题情景:如图直角中,,,,求的长?
解题思路:把的角转化成特殊角度,再利用特殊角度进行边之间的换算.
解决方案:方法一:延长至B,使得,过作,交于点,根据角平分线的性质定理和等腰直角三角形边的关系,可得
方法二:作的中垂线交于点F,连接,根据中垂线的性质定理和等腰直角三角形边的关务,设,,,,得,,则.
其他方法……
迁移应用解决新问题:如图直角中,,,,求的长,写出你的解答过程.
21.(12分)定义:如果一个三角形一边的平方与另一边上高的平方之和等于第三边的平方,则称这个三角形为“牵手三角形”,这条边与第三边的交点称为“牵手顶点”.例如图1,在中,,是边上的高,若,则为“牵手三角形”,点B为“牵手顶点”.
(1)等边三角形______“牵手三角形”(填写“是”或者“不是”);
(2)如图2,已知为“牵手三角形”,其中点A为“牵手顶点”,,是边上的高.在不添加其他线段和字母的情况下,找出图中一组相等的线段,并说明理由;
(3)运用(2)中的结论解决下列问题:
①已知为“牵手三角形”,其中点C为“牵手顶点”且,是边上的高.若,,则的长是______;
②如图3,为“牵手三角形”,其中,A为“牵手顶点”,是边上的高,,若,.求证:为等腰三角形.
答案以及解析
1.答案:C
解析:用反证法证明:在一个三角形中,至少有一个内角小于或等于时,
第一步先假设三角形中每个内角都大于,
故选:C.
2.答案:A
解析:,,
,
A.,符合两直角三角形全等的判定定理,故该选项符合题意;
B.,,不是两直角三角形全等的判定定理,故该选项不符合题意;
C.,不符合两直角三角形全等的判定定理,故该选项不符合题意;
D.,,不是两直角三角形全等的判定定理,故该选项不符合题意;
故选:A.
3.答案:D
解析:对于选项A,
故选项A不能判定为等腰三角形;
对于选项B,
可设,
解得:,
故选项B不能判定为等腰三角形;
对于选项C,
解得:,
此时不能确定和的度数,无法判定的形状,
故选项C不能判定为等腰三角形;
对于选项D,
三个角的度数之比是2:2:1
不妨假设,
可设,
解得:,
故选项D可以判定为等腰三角形.
故选:D
4.答案:D
解析:∵,
∴,,
设,
∴,
∴,
∵,
∴,
即,
解得:,
.
故答案为D.
5.答案:D
解析:在中,,若直线是的关于点B的二分割线,
∴①如图所示,当,,即是等腰三角形,是直角三角形,满足条件,
∴;
②如图所示,当,,即是直角三角形,是等腰三角形,满足条件,
∴,
∴;
③如图所示,当,,即是等腰三角形,是直角三角形,满足条件,
∴,
∵是的外角,
∴,
综上所述,的度数是或或,
故选:D.
6.答案:C
解析:连接,过M作于E,于F,
和分别平分和,,,
,,
的周长是,
,
的面积
,
故选:C.
7.答案:B
解析:由作图可知:,,
∴垂直平分,
又∵点E在上,
∴,故A正确,但不合题意;
∵,,
∴,又
∴,又
∴
∵垂直平分,
∴是等腰三角形,
∴
又,
∴,
∴,故C正确,但不符合题意.
由可知,垂直平分线段,
故D正确,但不符合题意.
由点A在线段的垂直平分线上知,
,
∴.
故B不正确,但符合题意.
故选:B.
8.答案:C
解析:如图,连接,.
∵是等腰三角形,点D是边的中点,
∴,
∴,解得.
∵是线段的垂直平分线,
∴点A关于直线的对称点为点C,,
∴,
∴的长为的最小值,
∴的周长.
故选:C.
9.答案:D
解析:∵和均是等边三角形,
∴,,
∴
∴
在和中
∴,
∴,∴①正确;
∴
∵
∴
∴在和中
∴,
∴,∴②正确;
∵
∴
∵
∴
∴,
∴③正确.故选D.
10.答案:D
解析:①∵是的外角平分线,,,
∴
∵D在的垂直平分线上,
∴,
∴,
故①正确;
在上截取,
∵
∴,,
∵,,
∴,
∵,
∴,,
,,
,
,
,
,
故④正确.
∵,
,
,,
∴,
∵,
∴,
∴;
故③正确;
∵,,
∴,,
,
∴,
,
,
∴,
即,故②正确;故选D.
11.答案:6
解析:作于F,
∵,是等腰三角形底边上的中线,
∴,
∵平分,,,
∴,
∴的面积,
故答案为:6.
12.答案:/度
解析:∵
∴,
又∵,
∴,
∴,
∴,
∵,
∴,
故答案为:.
13.答案:6
解析:∵是等边三角形,
,,
,
,
,
,
,
,
,
,
,
故答案为:6.
14.答案:6
解析:如图所示,过点O作,,垂足分别为H、G、P,连接,
∵平分,平分,
∴,
在中,,,,
∴,
∵,
∴,
∴,
∴,
∵过点O的直线平分面积,
∴,
∴,
∴,
∴,
故答案为:6.
15.答案:
解析:连接、,
∵点D为中点,是等腰直角三角形,
∴,
∵是等腰直角三角形,
∴,,
∴,
∴,
∴,,
∵,
∴,
∵,
∴,
∴,
∴当时,最小,此时
∴的最小值为,
故答案为:.
16.答案:(1)见解析
(2)见解析
解析:(1)证明:假设,则,这与已知相矛盾,
假设不成立,
a必为负数;
(2)证明:假设的整数部分k能化成两个整数的平方和,不妨设这两个整数为,,
则,
,
假设不成立,
的整数k不能化为两个整数的平方和.
17.答案:(1)是等腰三角形,见解析
(2)2
解析:(1)是等腰三角形.
理由:因为,
所以.
因为,
所以,
所以,,
所以.
因为,
所以,
所以,即为等腰三角形;
(2)因为,,
所以是等边三角形,
所以,.
因为,
所以.
因为F是的中点,
所以.
在中,,
所以.
18.答案:(1)作图见解析
(2)
解析:(1)如图,线段为所求作的图形;
(2)如图,
∵,,
∴为的垂直平分线,
∴,
∴,
所以当B,Q,P三点共线且时
此时的值最小,
∵,,
∴为等于直角三角形,,
∴,
即,
解得,
∴的最小值为.
19.答案:(1)见解析
(2)12
解析:(1)证明:过点E作于点F,如图所示:
∵,
∴,
∵是的平分线,
∴,
∵点E是的中点,
∴,
∴,
∴是的平分线;
(2)∵,,
∴,
∴,,
∵,,
∴,
∴,,
∴,
即,
∵,
∴.
20.答案:,见解析
解析:方法一:延长至B,使得,过作,交于点E.
∵,,,
∴.
∵,,
∴,.
∴,,
∴
∵,,
∴.
∴.
设,则:,,
∴,
∴,
∴.
方法二:作的中垂线交于点F,连接.
∵的中垂线交于点F,
∴.
∵,
∴.
∴.
∴.
∴,,
设,则,,
∴,
解得:.
∴.
21.答案:(1)不是
(2),理由见解析
(3)①8;②见解析
解析:(1)∵等边三角形的三边相等,
∴等边三角形一边的平方与另一边上高的平方之和大于第三边的平方,
∴等边三角形不是“牵手三角形”;
故答案为:不是
(2),理由如下:
∵为“牵手三角形”,是边上的高,
∴,
在中,,
∴,
∴;
(3)①如图,
由(2)得:,
在中,,
∴,
∴,
∴;
故答案为:8
②证明:由(2)得:,
∵,
∴和、均为直角三角形,
在和中,
∵,,
∴,
∴,,
∴,
∵,
∴,
即,
如图,延长交于点F,
在和中,
∵,,,
∴,
∴,
∵,
∴,
∴,
∴,∴为等腰三角形.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
