2024-2025学年人教版数学九年级(下)综合训练卷(含答案)
文档属性
| 名称 | 2024-2025学年人教版数学九年级(下)综合训练卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 477.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-11 15:08:29 | ||
图片预览


文档简介
2024-2025学年人教版数学九年级(下)综合训练卷
学校:___________姓名:___________班级:__________学号:___________
一、单选题
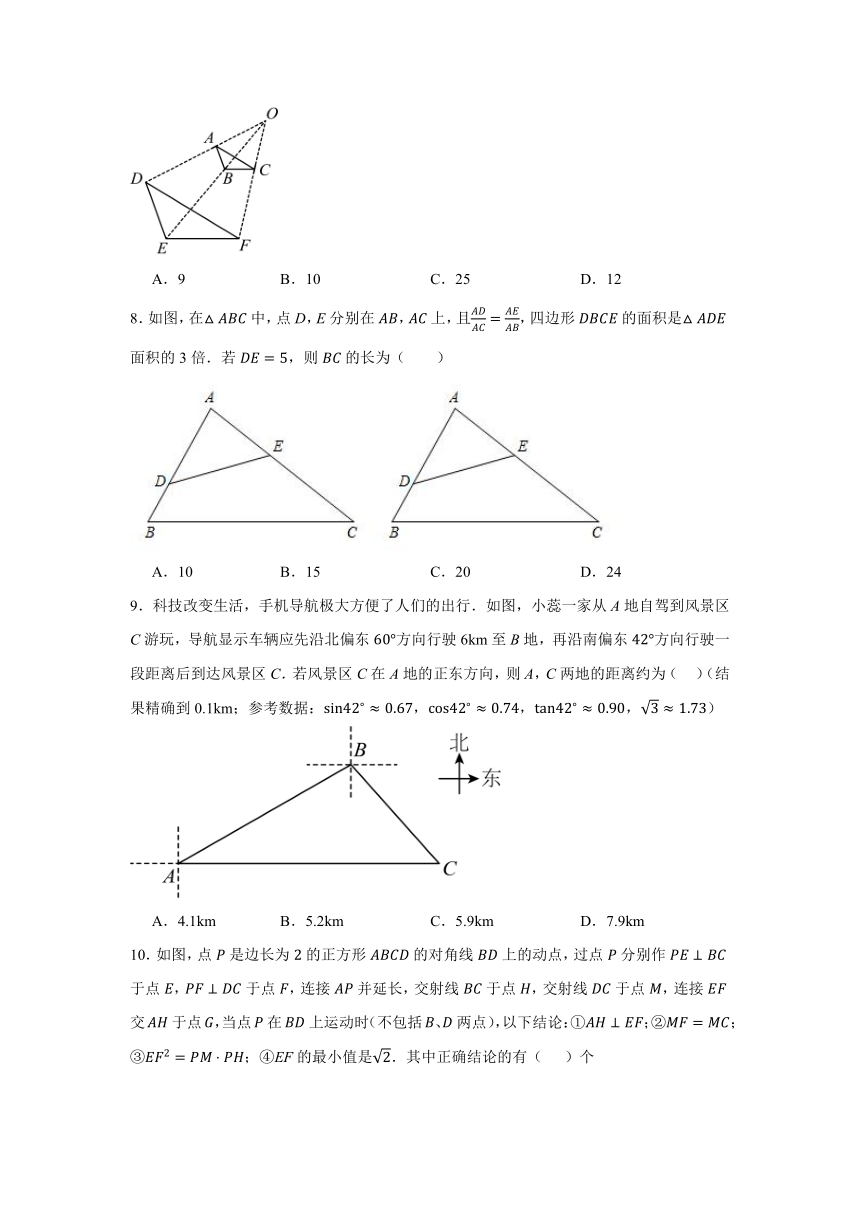
1.如图,直六棱柱的俯视图是( )
A. B.
C. D.
2.如果反比例函数的图像经过点,那么此反比例函数的解析式为( )
A. B. C. D.
3.在中,,,,则等于( )
A.3 B.2 C. D.
4.若,则的值为( )
A. B. C. D.
5.已知点在反比例函数的图象上,则( )
A. B. C. D.
6.一定质量的干松木,当它的体积V=2m3时,它的密度为ρ=0.5×103kg/m3,且ρ与V成反比例,则ρ与V的函数关系式为( )
A.ρ=1000V B.ρ=V+1000 C.ρ= D.ρ=
7.如图,已知和是以点为位似中心的位似图形,的面积为4,则的面积为( )
A.9 B.10 C.25 D.12
8.如图,在中,点D,E分别在,上,且,四边形的面积是面积的3倍.若,则的长为( )
A.10 B.15 C.20 D.24
9.科技改变生活,手机导航极大方便了人们的出行.如图,小蕊一家从A地自驾到风景区C游玩,导航显示车辆应先沿北偏东方向行驶6km至B地,再沿南偏东方向行驶一段距离后到达风景区C.若风景区C在A地的正东方向,则A,C两地的距离约为( )(结果精确到0.1km;参考数据:)
A.4.1km B.5.2km C.5.9km D.7.9km
10.如图,点是边长为的正方形的对角线上的动点,过点分别作于点,于点,连接并延长,交射线于点,交射线于点,连接交于点,当点在上运动时(不包括、两点),以下结论:①;②;③;④EF的最小值是.其中正确结论的有( )个
A.1 B.2 C.3 D.4
二、填空题
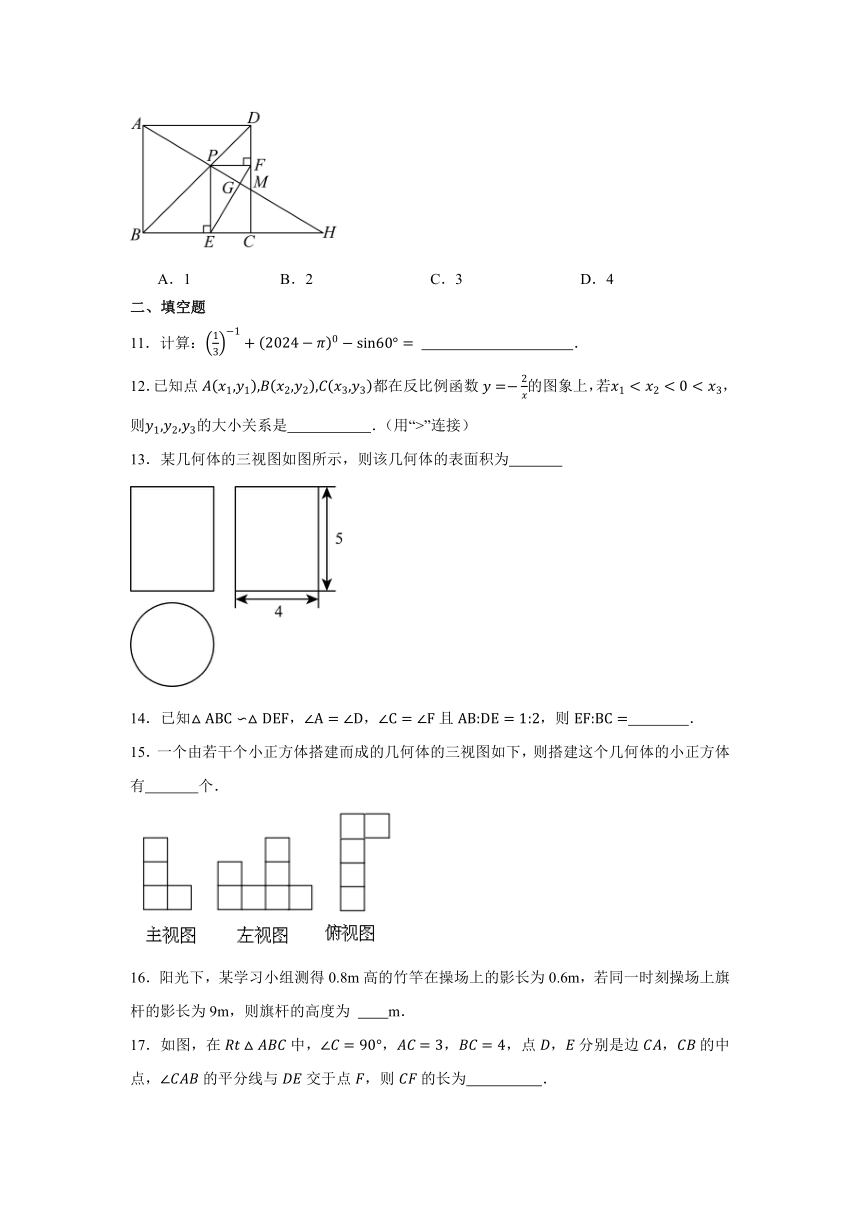
11.计算: .
12.已知点都在反比例函数的图象上,若,则的大小关系是 .(用“>”连接)
13.某几何体的三视图如图所示,则该几何体的表面积为
14.已知,,且,则 .
15.一个由若干个小正方体搭建而成的几何体的三视图如下,则搭建这个几何体的小正方体有 个.
16.阳光下,某学习小组测得0.8m高的竹竿在操场上的影长为0.6m,若同一时刻操场上旗杆的影长为9m,则旗杆的高度为 m.
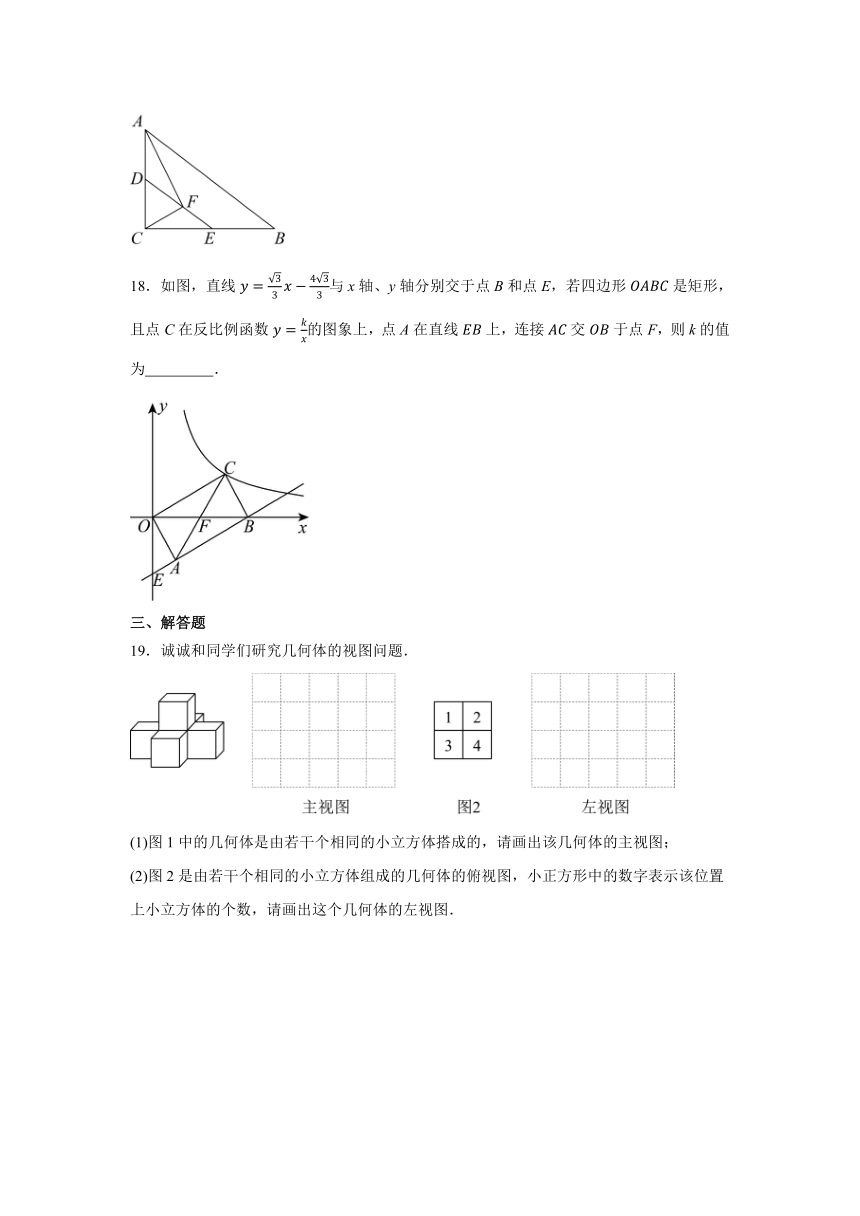
17.如图,在中,,,,点,分别是边,的中点,的平分线与交于点,则的长为 .
18.如图,直线与x轴、y轴分别交于点B和点E,若四边形是矩形,且点C在反比例函数的图象上,点A在直线上,连接交于点F,则k的值为 .
三、解答题
19.诚诚和同学们研究几何体的视图问题.
(1)图1中的几何体是由若干个相同的小立方体搭成的,请画出该几何体的主视图;
(2)图2是由若干个相同的小立方体组成的几何体的俯视图,小正方形中的数字表示该位置上小立方体的个数,请画出这个几何体的左视图.
20.如图,的顶点和定点O都在单位长度为1的正方形网格的格点上.
(1)以点O为位似中心,在网格纸中画出的位似,使它与的相似比为2,且位于点O的右侧;
(2)在(1)的情况下,线段经过格点D(不同于点,),连接,,直接写出四边形的形状及其面积.
21.小文和小君同学想利用数学知识测量矗立在教学楼边上的大树的高度.如图,他们在教学楼边上的处放置了一根垂直于地面的标杆,然后小文笔直地站在处,小君在和之间找到一个合适的位置,并在点处放置了一面小镜子,此时小文恰好看到在镜子里点和点重合.已知,点、、、在同一条直线上,通过测量,,,,小文的眼睛离地面的高度.求大树的高度.
22.我市某蔬菜生产基地在气温较低时,用装有恒温系统的大鹏栽培一种在自然光照且温度为的条件下生长最快的新品种,如图是某天恒温系统从开启到关闭及关闭后,大棚内温度随时间x(小时)变化的函数图象,其中段是双曲线y=的一部分.请根据图中信息解析下列问题:
(1)求y与x的函数关系式;
(2)当时,大棚内的温度约为多少度?
23.如图,在山顶上有一座电视塔,为测量山高,在地面上引一条基线,测得,已知电视塔高,求山高的值.(参考数据∶ 精确到)
24.如图,在以O为原点的直角坐标系中,点A、C分别在x轴、y轴的正半轴上,点B(a,b)在第一象限,四边形OABC是矩形,若反比例函数(k>0,x>0)的图象与AB相交于点D,与BC相交于点E,且BE=CE.
(1)求证:BD=AD;
(2)若四边形ODBE的面积是9,求k的值.
25.如图1,和均为等边三角形,连接BD,CE.
(1)直接写出BD与CE的数量关系为_________,直线BD与CE所夹锐角为__________度;
(2)将绕点A逆时针旋转至如图2,取BC,DE的中点M,N,连接MN,试问:的值是否随图形的旋转而变化?若不变,请求出该值;若变化,请说明理由;
(3)若,当图形旋转至B,D,E三点在一条直线上时,请画出图形,并直接写出MN的值为_______
参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 C A B B C D C A D C
11.
12.
13.
14.
15.8
16.12
17.
18.
19.(1)解:主视图如图所示:
(2)解:左视图如图所示,
20.(1)解:(1)如图,为所作;
(2)(2)如图,四边形为所求,
,,
四边形是平行四边形,
.
21.解:,,
,
,
,
,
,,
,
,
答:大树的高度为12米.
22.(1)解:设解析式是,则,解得,
∴.
∵双曲线y=经过,
∴,解得.
∴.
综上所述,y与x的函数解析式为:;
(2)当时,.
答:当时,大棚内的温度约为13.5度.
23.解:设,
在中,,
,
,
在中,,
,
,
,
,
即,
解得:,
即山高的值约为.
24.9
25.(1) 与是等边三角形,
,,,
,.
在与中,
,
.
,.
,
即,
直线与所夹锐角为.
(2)解:不变,理由如下:
连接,.
、分别为、的中点,且与是等边三角形,
,,
,,
,
,,
,
,
.
(3)解:分两种情况讨论:
如图所示,连接.
由(2)得,,.
,,
,,
,
,
,即;
如图所示,连接.
由①得,,,
,
,即.
综上,的值为或.
学校:___________姓名:___________班级:__________学号:___________
一、单选题
1.如图,直六棱柱的俯视图是( )
A. B.
C. D.
2.如果反比例函数的图像经过点,那么此反比例函数的解析式为( )
A. B. C. D.
3.在中,,,,则等于( )
A.3 B.2 C. D.
4.若,则的值为( )
A. B. C. D.
5.已知点在反比例函数的图象上,则( )
A. B. C. D.
6.一定质量的干松木,当它的体积V=2m3时,它的密度为ρ=0.5×103kg/m3,且ρ与V成反比例,则ρ与V的函数关系式为( )
A.ρ=1000V B.ρ=V+1000 C.ρ= D.ρ=
7.如图,已知和是以点为位似中心的位似图形,的面积为4,则的面积为( )
A.9 B.10 C.25 D.12
8.如图,在中,点D,E分别在,上,且,四边形的面积是面积的3倍.若,则的长为( )
A.10 B.15 C.20 D.24
9.科技改变生活,手机导航极大方便了人们的出行.如图,小蕊一家从A地自驾到风景区C游玩,导航显示车辆应先沿北偏东方向行驶6km至B地,再沿南偏东方向行驶一段距离后到达风景区C.若风景区C在A地的正东方向,则A,C两地的距离约为( )(结果精确到0.1km;参考数据:)
A.4.1km B.5.2km C.5.9km D.7.9km
10.如图,点是边长为的正方形的对角线上的动点,过点分别作于点,于点,连接并延长,交射线于点,交射线于点,连接交于点,当点在上运动时(不包括、两点),以下结论:①;②;③;④EF的最小值是.其中正确结论的有( )个
A.1 B.2 C.3 D.4
二、填空题
11.计算: .
12.已知点都在反比例函数的图象上,若,则的大小关系是 .(用“>”连接)
13.某几何体的三视图如图所示,则该几何体的表面积为
14.已知,,且,则 .
15.一个由若干个小正方体搭建而成的几何体的三视图如下,则搭建这个几何体的小正方体有 个.
16.阳光下,某学习小组测得0.8m高的竹竿在操场上的影长为0.6m,若同一时刻操场上旗杆的影长为9m,则旗杆的高度为 m.
17.如图,在中,,,,点,分别是边,的中点,的平分线与交于点,则的长为 .
18.如图,直线与x轴、y轴分别交于点B和点E,若四边形是矩形,且点C在反比例函数的图象上,点A在直线上,连接交于点F,则k的值为 .
三、解答题
19.诚诚和同学们研究几何体的视图问题.
(1)图1中的几何体是由若干个相同的小立方体搭成的,请画出该几何体的主视图;
(2)图2是由若干个相同的小立方体组成的几何体的俯视图,小正方形中的数字表示该位置上小立方体的个数,请画出这个几何体的左视图.
20.如图,的顶点和定点O都在单位长度为1的正方形网格的格点上.
(1)以点O为位似中心,在网格纸中画出的位似,使它与的相似比为2,且位于点O的右侧;
(2)在(1)的情况下,线段经过格点D(不同于点,),连接,,直接写出四边形的形状及其面积.
21.小文和小君同学想利用数学知识测量矗立在教学楼边上的大树的高度.如图,他们在教学楼边上的处放置了一根垂直于地面的标杆,然后小文笔直地站在处,小君在和之间找到一个合适的位置,并在点处放置了一面小镜子,此时小文恰好看到在镜子里点和点重合.已知,点、、、在同一条直线上,通过测量,,,,小文的眼睛离地面的高度.求大树的高度.
22.我市某蔬菜生产基地在气温较低时,用装有恒温系统的大鹏栽培一种在自然光照且温度为的条件下生长最快的新品种,如图是某天恒温系统从开启到关闭及关闭后,大棚内温度随时间x(小时)变化的函数图象,其中段是双曲线y=的一部分.请根据图中信息解析下列问题:
(1)求y与x的函数关系式;
(2)当时,大棚内的温度约为多少度?
23.如图,在山顶上有一座电视塔,为测量山高,在地面上引一条基线,测得,已知电视塔高,求山高的值.(参考数据∶ 精确到)
24.如图,在以O为原点的直角坐标系中,点A、C分别在x轴、y轴的正半轴上,点B(a,b)在第一象限,四边形OABC是矩形,若反比例函数(k>0,x>0)的图象与AB相交于点D,与BC相交于点E,且BE=CE.
(1)求证:BD=AD;
(2)若四边形ODBE的面积是9,求k的值.
25.如图1,和均为等边三角形,连接BD,CE.
(1)直接写出BD与CE的数量关系为_________,直线BD与CE所夹锐角为__________度;
(2)将绕点A逆时针旋转至如图2,取BC,DE的中点M,N,连接MN,试问:的值是否随图形的旋转而变化?若不变,请求出该值;若变化,请说明理由;
(3)若,当图形旋转至B,D,E三点在一条直线上时,请画出图形,并直接写出MN的值为_______
参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 C A B B C D C A D C
11.
12.
13.
14.
15.8
16.12
17.
18.
19.(1)解:主视图如图所示:
(2)解:左视图如图所示,
20.(1)解:(1)如图,为所作;
(2)(2)如图,四边形为所求,
,,
四边形是平行四边形,
.
21.解:,,
,
,
,
,
,,
,
,
答:大树的高度为12米.
22.(1)解:设解析式是,则,解得,
∴.
∵双曲线y=经过,
∴,解得.
∴.
综上所述,y与x的函数解析式为:;
(2)当时,.
答:当时,大棚内的温度约为13.5度.
23.解:设,
在中,,
,
,
在中,,
,
,
,
,
即,
解得:,
即山高的值约为.
24.9
25.(1) 与是等边三角形,
,,,
,.
在与中,
,
.
,.
,
即,
直线与所夹锐角为.
(2)解:不变,理由如下:
连接,.
、分别为、的中点,且与是等边三角形,
,,
,,
,
,,
,
,
.
(3)解:分两种情况讨论:
如图所示,连接.
由(2)得,,.
,,
,,
,
,
,即;
如图所示,连接.
由①得,,,
,
,即.
综上,的值为或.
