2024-2025学年北师大版五年级数学上册期末冲刺卷(含答案)
文档属性
| 名称 | 2024-2025学年北师大版五年级数学上册期末冲刺卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-09 21:23:49 | ||
图片预览



文档简介
保密★启用前
20224-2025学年五年级上册期末冲刺卷(北师大版)
数学
考试范围:五上全册 考试时间:100分钟 分值:100分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
一、精挑细选,慎重选择。(请在答题卡相应位置作答)(共9分)
1.一本书共90页,明明第一天看了第二天应从第( )页看起。
A.14 B.15 C.16
2.( )都是轴对称图形。
A. B. C.
3.下列说法正确的是( )。
A.所有的偶数都是合数,所有的奇数都是质数
B.把分数约分后,分数大小不变,分数单位也不变
C.由三个连续自然数组成的三位数一定是3的倍数
D.平行四边形是轴对称图形
4.两个奇数的和,一定是( )
A.奇数 B.偶数 C.质数 D.合数
5.如图中的网格阴影部分可以用算式( )表示。
A. B. C.
6. 下面算式的商是循环小数的是( )。
A.1.38÷0.5 B.0.65÷0.4 C.0.28÷1.5 D.3.69÷0.3
7.一块周长为24000米的正方形土地, 面积是36( )。
A.平方米 B.公顷 C.平方千米 D.千米
8.既有因数2,又有因数3,同时又是5的倍数的数是( )
A.320 B.540 C.405
9.小明和小华下棋,需要想个办法决定谁先走,下列方法中,不公平的是( )
A.玩“石头、剪刀、布”的游戏,谁赢谁先走。
B.同时抛2枚硬币,2枚硬币的数字面都朝上,小明先走:其它情况,小华先走。
C.掷骰子,点数大于3,小明先走:点数小于4,小华先走。
D.红球、黄球各3个,放入袋中,每次摸一个,然后放回。摸到红球,小明先走:到黄球,小华先走。
二、火眼金睛,细心裁判。(共6分)
10.循环小数一定是无限小数,无限小数不一定是循环小数。
11.所有的质数都是奇数,所有的合数都是偶数。
12.用三个大小一样的正方形拼成一个最大的长方形,这个长方形的面积是正方形面积的3倍,周长是正方形周长的2倍。( )
13.把一个长方形木框架拉成平行四边形,周长不变,面积变小了.( )
14.抛硬币10次,正面朝上和反面朝上的次数肯定都有5次。( )
15.把一个平行四边形樞架拉成一个长方形, 这个长方形的周长与原来平行四边形的周长相等。( )
三、欢乐填空,对号入座。(把答案填到答题卡相应位置上)(共23分)。
16. 数轴上点 用分数表示为 ,它的分数单位是 , 再添上 个这样的分数单位就是最小的质数。
17.用火柴棒摆汉字。如图所示,奇奇用一捆长度相等的小棒刚好摆了 3个“口”字,如果用这些小棒摆“十”字,可以摆出 个“十”字。
18.的分数单位是 ,它有 个这样的分数单位,再添 个这样的分数单位就是最小的质数。
19.120 米的是 米; 吨的是 42 吨。
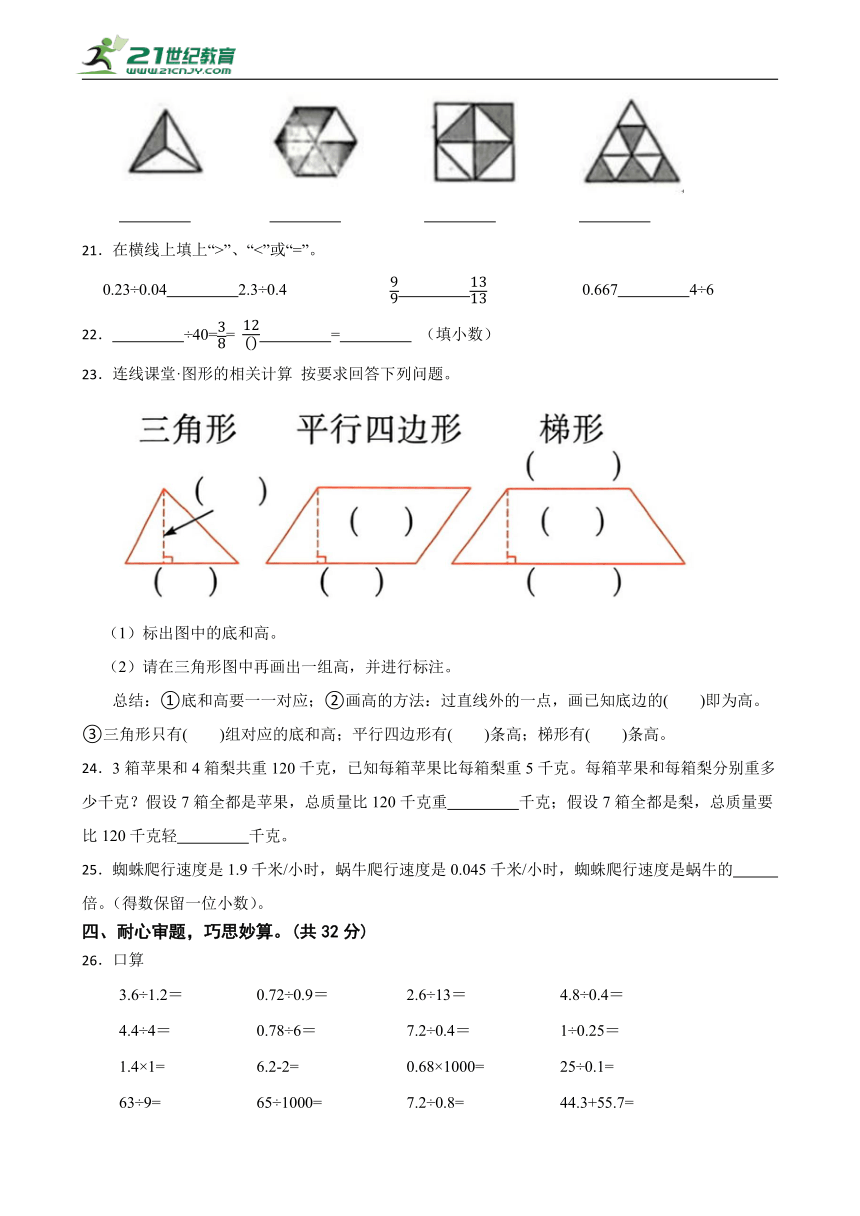
20.用分数表示下图中的涂色部分。
21.在横线上填上“>”、“<”或“=”。
0.23÷0.04 2.3÷0.4 0.667 4÷6
22. ÷40== = (填小数)
23.连线课堂·图形的相关计算 按要求回答下列问题。
(1)标出图中的底和高。
(2)请在三角形图中再画出一组高,并进行标注。
总结:①底和高要一一对应;②画高的方法:过直线外的一点,画已知底边的( )即为高。③三角形只有( )组对应的底和高;平行四边形有( )条高;梯形有( )条高。
24.3箱苹果和4箱梨共重120千克,已知每箱苹果比每箱梨重5千克。每箱苹果和每箱梨分别重多少千克?假设7箱全都是苹果,总质量比120千克重 千克;假设7箱全都是梨,总质量要比120千克轻 千克。
25.蜘蛛爬行速度是1.9千米/小时,蜗牛爬行速度是0.045千米/小时,蜘蛛爬行速度是蜗牛的 倍。(得数保留一位小数)。
四、耐心审题,巧思妙算。(共32分)
26.口算
3.6÷1.2= 0.72÷0.9= 2.6÷13= 4.8÷0.4=
4.4÷4= 0.78÷6= 7.2÷0.4= 1÷0.25=
1.4×1= 6.2-2= 0.68×1000= 25÷0.1=
63÷9= 65÷1000= 7.2÷0.8= 44.3+55.7=
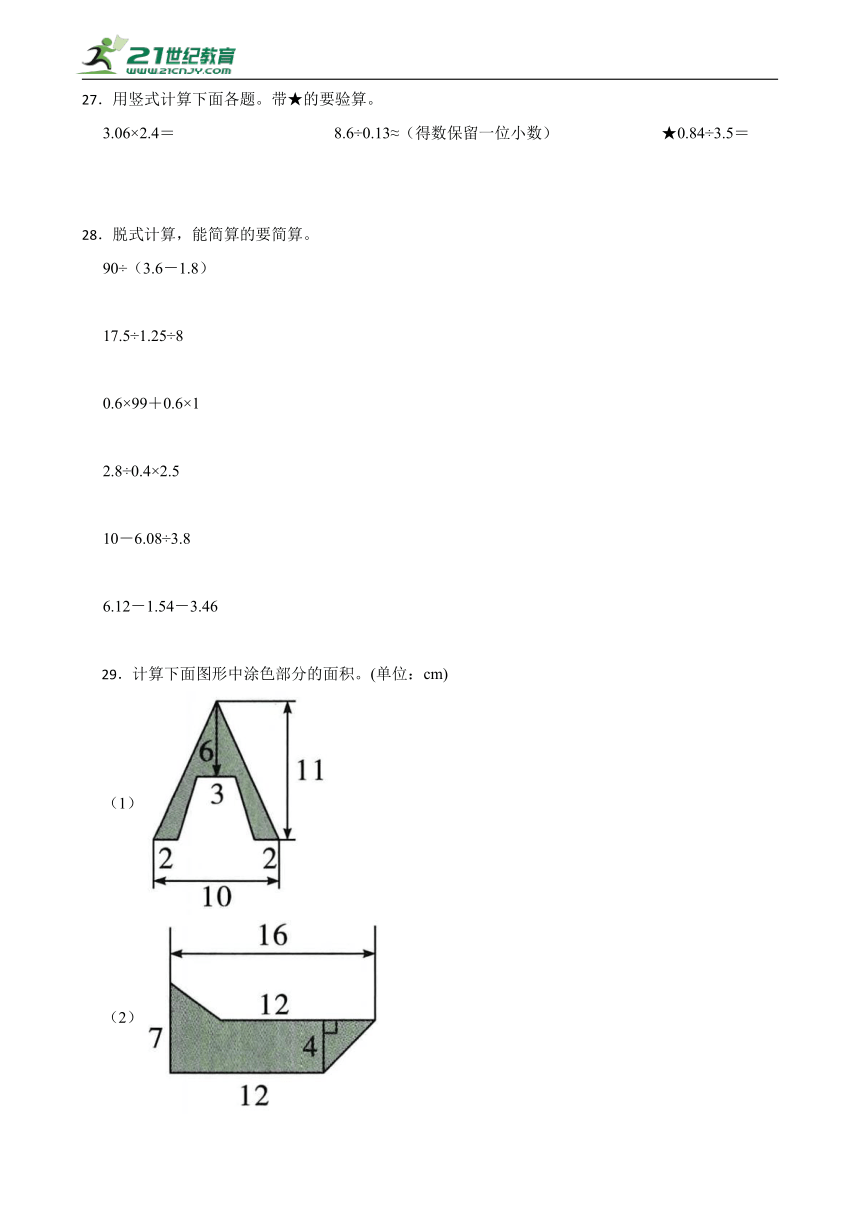
27.用竖式计算下面各题。带★的要验算。
3.06×2.4= 8.6÷0.13≈(得数保留一位小数) ★0.84÷3.5=
28.脱式计算,能简算的要简算。
90÷(3.6-1.8)
17.5÷1.25÷8
0.6×99+0.6×1
2.8÷0.4×2.5
10-6.08÷3.8
6.12-1.54-3.46
29.计算下面图形中涂色部分的面积。(单位:cm)
(1)
(2)
五、仔细观察,认真操作。(共6分)
30.按要求画一画。
(1)以虚线MN为对称轴,画出图形①的轴对称图形。
(2)画出图形①先向左平移3格,再向上平移2格后的图形。
(3)画出图形②绕点O顺时针旋转90°后的图形。
(4)画出图形②放大后的图形,使放大后的图形与原图形对应线段长的比为2:1。
(5)图形③中顶点A用数对表示为(3,2),将表示图形③轮廓点数对的第一个数乘3,第二个数不变,画出得到的图形。
六、走进生活,解决问题。(共24分)
31.圆圈代表干果,用不同颜色或方式涂一涂、说一说,小刺猬和小松鼠谁吃掉的干果更多?
客厅地面的面积为31 m2,如果用边长为0. 6 m的正方形地砖铺地面,86块够吗?
从前有个农民,临死前留下遗言,要把17头牛分给三个儿子,其中大儿子分得,二儿子分得,小儿子分得,但不能把牛卖掉或杀掉。三个儿子按照老人的要求怎么也分不好。后来一位邻居顺利地帮他们把17头牛分完了,你知道是怎么分的吗?
34.某地研究的高产技术使得新型小麦的产量可以达到每公顷9300千克,如果在如图所示的区域内种植该新型小麦,一共可以收获多少千克小麦 (单位:米)
35.阳春三月正是踏青好时节,冬冬旅行社推出“西游洞风景区一日 游”的两种价格方案。
(1)小红和小华约上几个朋友,连同家人计划参加“西游洞风景区一 日游”,他们的计划中有成人 5 人,儿童 8 人,选哪种方案合算?
(2)实际出发时,在计划的基础上增加了2名成人,此时选哪种方案合算?
答案解析部分
1.C
解:90×=15(页)
15+1=16(页)
故答案为:C。
明明第一天看的页数=这本书的页数×明明第一天看的分率,所以第二天看起的页数就是在第一天看的基础上加1页即可。
2.B
解: 这两个图形对折后能够完全重合,是轴对称图形。
故答案为:B。
依据轴对称图形的定义判断:平面内,一个图形沿一条直线折叠,直线两旁的部分能够完全重合,这个图形就是轴对称图形;其中的这条直线就是对称轴。
3.C
解:A:2是偶数不是合数,该选项说法错误;
B:把分数约分后,分数大小不变,分数单位改变,该选项说法错误;
C:由三个连续自然数组成的三位数一定是3的倍数,该选项说法正确;
D:平行四边形不是轴对称图形,该选项说法错误。
故答案为:C。
不能被2整除的数是奇数,能被2整除的数是偶数;一个数,如果只有1和它本身两个因数,这样的数叫做质数;一个数,除了1和它本身还有别的因数,这样的数叫做合数;
一个分数的分数单位就是分母分之一;
3的倍数的特征是这个数的所有数位上的数字之和是3的倍数;
如果一个图形沿着一条直线对折,两侧的图形能够完全重合,这个图形就是轴对称图形。
4.B
奇数+奇数=偶数.
故答案为:B
奇数是不能被2整除的数,两个奇数的和一定是偶数.
5.B
把整个长方形看作单位“1”,先取整个长方形的,再从取的中取,也就是,用乘法算式:
故答案为:B
可根据分数乘法的意义,求一个数的几分之几是多少用乘法计算来确定算式。
6.C
解:A:,得出的商是有限小数,不符合题意。
B:,得出的商是有限小数,不符合题意。
C:,观察到小数点后出现了周期性的数字重复(6的循环),故商是循环小数,符合题意。
D:,得出的商是有限小数,不符合题意。
故答案为:C。
循环小数的特点是在小数点后某个位置开始出现周期性的数字重复。对于这类问题,最直接的方法是计算每个选项的具体结果,观察商是否出现循环。
7.C
解:24000÷4=6000(米)
6000×6000=36000000(平方米)
36000000平方米=36平方千米
故答案为:C。
正方形的周长÷4=正方形的边长,正方形的边长×正方形的边长=正方形的面积;1平方千米=1000000平方米,把高级单位换算成低级单位要乘进率,把低级单位换算成高级单位要除以进率。
8.B
解:A:320有因数2和5;
B:540既有因数2,又有因数3,同时又有因数5;
C:405有因数3和5。
故答案为:B。
同时有因数2、3、5的数的个位数字一定是0,且各个数位上数字之和是3的倍数。
9.B
解:A:玩“石头、剪刀、布”的游戏,由于石头赢剪刀,剪刀赢布,布赢石头,形成一个循环,每种出拳方式赢的概率都是,因此小明和小华先走的概率都是 ,游戏规则公平。
B:同时抛2枚硬币,有正正、正反、反正、反反4种结果,其中只有正正1种结果是两枚硬币的数字面都朝上,其余3种情况小华先走,所以小明先走的概率是,小华先走的概率是,游戏规则不公平;
C:掷骰子,点数大于3(即4、5、6)有3种情况,小明先走;点数小于4(即1、2、3)有3种情况,小华先走。小明和小华先走的概率都是,游戏规则公平;
D:红球、黄球各3个,放入袋中,每次摸一个,然后放回。摸到红球小明先走,摸到黄球小华先走。因为红球和黄球的数量相同,所以小明和小华先走的概率都是 ,游戏规则公平。
故答案为:B。
要判断这些决定谁先走的游戏规则是否公平,需要考察每种情况下小明和小华先走的概率是否相等。如果概率相等,则游戏规则是公平的;反之,则是不公平的。
10.正确
循环小数一定是无限小数,无限小数不一定是循环小数,此题说法正确.
故答案为:正确.
小数可以分成有限小数和无限小数,小数部分的数位是有限的小数,叫做有限小数;小数部分的数位是无限的小数,叫做无限小数;无限小数分为循环小数和无限不循环小数,循环小数一定是无限小数,无限小数不一定是循环小数,据此判断.
11.错误
解:2是偶数,也是质数。
故答案为:错误。
;除了1和本身外还有其它因数的数是合数;只有1和本身两个因数的数是质数;2既是偶数,也是质数。
12.正确
解:如图,假设正方形的边长是1,
3÷1=3,这个长方形的面积是正方形面积的3倍,
长方形的周长(3+1)×2=8(厘米),正方形的周长1×4=4(厘米)
8÷4=2,周长是正方形周长的2倍,原题说法正确。
故答案为:正确。
(长+宽)×2=长方形的周长;长×宽=长方形的面积;正方形的边长×4=正方形的周长;正方形的边长×边长=正方形的面积。
13.正确
解:把一个长方形木框架拉成平行四边形,周长不变,面积变小了,说法正确。
故答案为:正确。
一个长方形框架拉成平行四边形,四条边的边长不变则周长不变;再拉的过程中,底不变,高减小,根据平行四边形的面积=底×高即可得出答案。
14.错误
解:抛硬币10次,正面朝上和反面朝上的次数不是确定的事件,原题说法错误。
故答案为:错误。
抛硬币的可能性是正面朝上和方面朝上,但是出现的次数是不确定的,据此判断。
15.正确
解:把一个平行四边形框架拉成一个长方形,这个长方形的周长与原来平行四边形的周长相等,说法正确。
故答案为:正确。
把一个平行四边形框架拉成一个长方形,只是改变了图形的形状,没有改变原图形四条边的长度,所以这个长方形的周长与原来平行四边形的周长相等。
16.;7;3
解:点A=,它的分数单位是;
2-=,再添上3个这样的分数单位就是最小的质数。
故答案为:;7;3。
最小的质数是2,分数中的分母表示把单位“1”平均分的份数,分子表示取的份数,分子是几,就表示有几个这样的分数单位。
17.6
解:4÷2=2(个),2×3=6(个),所以可以摆出6个“十”字。
故答案为:6。
一个“口”字有4根小棒,一个“十”字有2根小棒,所以一个“口”字可以摆4÷2=2(个)“十”字,所以一共可以摆“十”字的个数=“口”字的个数×一个“口”字可以摆“十”字的的个数。
18.;4;14
解:的分数单位就是,它有4个这样的分数单位;
最小的质数是2,2=,有18个这样的分数单位;
18-4=14(个);
故答案为:;4;14。
一个分数的分母是几,它的分数单位就是几分之一;分子是几就有几个这样的分数单位;
表示把单位“1”平均分成9份,每份是,根据分数单位的定义,它的分数单位就是;分子是4,所以它有4个这样的分数单位 ;
最小的质数是2,把2化成分母是9的分数得,有18个这样的分数单位,因此再加上18-4=14(个) 这样的分数单位就是最小的质数 。
19.48;36
解:120×=48(米)
42÷=36(吨)
故答案为:48,36。
求一个数的几分之几是多少,利用分数乘法计算即可;已知一个数的几分之几是a,只需用a除以分数,即可求出这个数。
20.;;;
解:涂色部分用分数表示依次是:;;;。
故答案为:;;;。
分数中的分母表示把单位“1”平均分的份数,分子表示取的份数,涂色部分占几份,分子就是几。
21.=;=;>
解:0.23的小数点向右移动一位变成2.3,0.04的小数点向右移动一位变成0.4,商不变,0.23÷0.04=2.3÷0.4;
=1,=1,=;
因为4÷6=0.66……,0.667>0.66……,所以0.667>4÷6。
故答案为:=;=;>。
商不变的规律:在除法里,被除数和除数同时扩大或者同时缩小相同的倍数,商不变;
分子和分母相同的分数,可以写成整数1;
比较小数与除法的关系,先算出除法的商,再比较小数的大小,先看它们的整数部分,整数部分大的那个数就大;整数部分相同的,十分位上的数大的那个数就大;十分位上的数也相同的,百分位上的数大的那个数就大……。
22.15;32;0.375
解:40×=15;12÷=32;=3÷8=0.375。
故答案为:15;32;0.375。
被除数=除数×商;分母=分子÷分数值;分数化小数:用分子除以分母,商写成小数的形式。
23.(1)
(2)垂线,3,无数,无数
24.20;15
解:(120+20)÷7
=140÷7
=20(千克)
(120-15)÷7
=105÷7
=15(千克)
故答案为:20;15。
每箱苹果比每箱梨重5千克 , 假设7箱全都是苹果 ,则总质量为(120+20)=140(千克),那么总质量比120千克重140-120=20(千克); 假设7箱全都是梨,则总质量为(120-15)=105(千克),那么总质量比120千克轻120-105=15(千克)。
25.42.2
解:1.9÷0.045≈42.2。
故答案为:42.2。
蜘蛛爬行速度是蜗牛的倍数=蜘蛛爬行的速度÷蜗牛爬行的速度。
26.
3.6÷1.2=3 0.72÷0.9=0.8 2.6÷13=0.2 4.8÷0.4=12
4.4÷4=1.1 0.78÷6=0.13 7.2÷0.4=18 1÷0.25=4
1.4×1=1.4 6.2-2=4.2 0.68×1000=680 25÷0.1=250
63÷9=7 65÷1000=0.065 7.2÷0.8=9 44.3+55.7=100
除数是整数的小数除法计算法则:先按照整数除法的法则去除,商的小数点要和被除数的小数点对齐;如果除到被除数的末尾仍有余数,就在余数后面添“0”,再继续除;
除数是小数的除法计算法则:先移动除数的小数点,使它变成整数,除数的小数点向右移动几位,被除数的小数点也向右移动几位(位数不够的补“0”),然后按照除数是整数的除法法则进行计算;
一个数乘10、100、1000……直接把它的小数点向右移动一位、两位、三位……;
一个数除以10、100、1000……,直接把它的小数点向左移动一位、两位、三位……;
计算小数加减法时,先把小数点对齐,也就是相同数位对齐,然后再按照整数加减法的计算法则进行计算。
27.7.344;66.2;0.24
28.解: 90÷(3.6-1.8)
=90÷1.8
=5
17.5÷1.25÷8
=17.5÷(1.25×8)
=17.5÷10
=1.75
0.6×99+0.6×1
=0.6×(99+1)
=0.6×100
=60
2.8÷0.4×2.5
=7×2.5
=17.5
10-6.08÷3.8
=10-1.6
=8.4
6.12-1.54-3.46
=6.12-(1.54+3.46)
=6.12-5
=1.12
第一题:根据四则混合运算顺序进行计算。
第二题:根据连续除以两个数等于除以这两个数的积进行简便计算
第三题:根据乘法分配律进行简便计算。
第四题:按照乘除法计算顺序进行计算。
第五题:根据四则混合运算顺序进行计算。
第六题:根据连续减去两个数等于减去这两个数的和进行简便计算。
29.(1)解:如图,三角形的面积
梯形的面积=(3+10-2-2)×(11-6)÷2=22.5(cm2),
所以涂色部分的面积=S三角形-S梯形=55-22.5=32.5(cm2)。
(2)解:如图,将涂色部分看作是三角形与平行四边形的组合,
三角形的面积
平行四边形的面积
所以涂色部分的面积
(1)本题要求解的是涂色部分的面积,通过题目描述和计算公式,可以看出需要先分别计算出三角形和梯形的面积,然后用三角形的面积减去梯形的面积,从而得到涂色部分的面积。
(2)本题要求求解由三角形和平行四边形组合而成的涂色部分的面积。根据题目给出的信息,首先计算三角形的面积,再计算平行四边形的面积,最后将两者相加得到涂色部分的总面积。
30.(1)解:
(2)解:
(3)解:
(4)解:
(5)解:
(1)补全轴对称图形,先过这个图形的关键点作对称轴的垂线,然后数出关键点到对称轴的格子数,并在另一边相同格子数的位置作上标记,最后把这些标记连接起来即可;
(2)作平移后的图形,先把关键点平移相同的格子数,然后把这些关键点连接起来即可;
(3)绕图形上一点顺时针旋转一定的度数,先把这个点连接的边顺时针旋转相同的度数,然后把剩下的边连接起来即可;
(4)把图形按照2:1放大,就是把这个图形的每条边都扩大2倍;
(5)数对中第一个数是几,表示这个点在第几列,第二个数是几,表示这个点在第几行。
31.解:12÷3=4(个)
12÷2=6(个)
答:小刺猬吃掉4个干果,小松鼠吃掉6个干果,故小松鼠吃掉的干果更多。
小刺猬、小松鼠分别吃松果的个数=松果的总个数÷各自分率的分母×分子,然后再比较大小。
32.解:0. 6×0. 6×86
=0. 36×86
=30. 96(m2)
30.96<31
答:86块不够。
用每块地砖的面积乘86求出地砖的总面积,然后与客厅面积比较后判断地砖够不够即可。
33.解:17头牛再借1头共18头,
大儿子分得:18×=9(头)
二儿子分得:18×=6(头)
小儿子分得:18×=2(头)
三个儿子一共分了:9+6+2=17(头)
剩下的一头还回去即可
答:大儿子分得9头牛,二儿子分得6头牛,小儿子分得2头牛。
因为2、3、9的最小公倍数是18,所以再借一头就可以直接分了;牛的总头数×= 大儿子分的头数,牛的总头数×=二儿子分的头数,牛的总头数×=小儿子分的头数,分完还余下一头,再还回去就可以了。
34.解:梯形的面积:
(20+35)×50÷2=1375(平方米)
三角形的面积:
24×40÷2=480(平方米)
平行四边形的面积:
12×35=420(平方米)
种植区域的面积:
1375+480+420=2275(平方米)=0.2275(公顷),
0.2275×9300=2115.75(千克)。
答:一共可以收获2115.75千克小麦。
观察图形,可知,小麦种植区域的面积等于以上底为20,下底为35,高为50的梯形的面积加上以底为40,高为24的三角形面积再加上以高为12,底为35的平行四边形的面积,利用梯形的面积公式:S=(上底+下底)×高÷2,三角形的满级公式:S=底×高÷2,平行四边形的面积公式:S=ah,然后代入数据即可,再将平方米化为公顷,最后再将面积乘以每公顷的产量,即可求解
35.(1)解:方案 1:
5×120+8×50
=600+400
=1000(元)
方案 2:
(5+8)×80
=13×80
=1040(元)
1000<1040。
答:选择方案1合算。
(2)解:方案 1:
(2+5)×120+8×50
=840+400
=1240(元)
方案 2:
(2+5+8)×80
=15×80
=1200(元)
1200<1240
答:选择方案2合算。
方案1:成人每人的钱数×人数+儿童每人的钱数×人数=一共需要的钱数;
方案2:总人数×每人的钱数=一共需要的钱数;
哪种方案花钱少,选哪种方案合算。
20224-2025学年五年级上册期末冲刺卷(北师大版)
数学
考试范围:五上全册 考试时间:100分钟 分值:100分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
一、精挑细选,慎重选择。(请在答题卡相应位置作答)(共9分)
1.一本书共90页,明明第一天看了第二天应从第( )页看起。
A.14 B.15 C.16
2.( )都是轴对称图形。
A. B. C.
3.下列说法正确的是( )。
A.所有的偶数都是合数,所有的奇数都是质数
B.把分数约分后,分数大小不变,分数单位也不变
C.由三个连续自然数组成的三位数一定是3的倍数
D.平行四边形是轴对称图形
4.两个奇数的和,一定是( )
A.奇数 B.偶数 C.质数 D.合数
5.如图中的网格阴影部分可以用算式( )表示。
A. B. C.
6. 下面算式的商是循环小数的是( )。
A.1.38÷0.5 B.0.65÷0.4 C.0.28÷1.5 D.3.69÷0.3
7.一块周长为24000米的正方形土地, 面积是36( )。
A.平方米 B.公顷 C.平方千米 D.千米
8.既有因数2,又有因数3,同时又是5的倍数的数是( )
A.320 B.540 C.405
9.小明和小华下棋,需要想个办法决定谁先走,下列方法中,不公平的是( )
A.玩“石头、剪刀、布”的游戏,谁赢谁先走。
B.同时抛2枚硬币,2枚硬币的数字面都朝上,小明先走:其它情况,小华先走。
C.掷骰子,点数大于3,小明先走:点数小于4,小华先走。
D.红球、黄球各3个,放入袋中,每次摸一个,然后放回。摸到红球,小明先走:到黄球,小华先走。
二、火眼金睛,细心裁判。(共6分)
10.循环小数一定是无限小数,无限小数不一定是循环小数。
11.所有的质数都是奇数,所有的合数都是偶数。
12.用三个大小一样的正方形拼成一个最大的长方形,这个长方形的面积是正方形面积的3倍,周长是正方形周长的2倍。( )
13.把一个长方形木框架拉成平行四边形,周长不变,面积变小了.( )
14.抛硬币10次,正面朝上和反面朝上的次数肯定都有5次。( )
15.把一个平行四边形樞架拉成一个长方形, 这个长方形的周长与原来平行四边形的周长相等。( )
三、欢乐填空,对号入座。(把答案填到答题卡相应位置上)(共23分)。
16. 数轴上点 用分数表示为 ,它的分数单位是 , 再添上 个这样的分数单位就是最小的质数。
17.用火柴棒摆汉字。如图所示,奇奇用一捆长度相等的小棒刚好摆了 3个“口”字,如果用这些小棒摆“十”字,可以摆出 个“十”字。
18.的分数单位是 ,它有 个这样的分数单位,再添 个这样的分数单位就是最小的质数。
19.120 米的是 米; 吨的是 42 吨。
20.用分数表示下图中的涂色部分。
21.在横线上填上“>”、“<”或“=”。
0.23÷0.04 2.3÷0.4 0.667 4÷6
22. ÷40== = (填小数)
23.连线课堂·图形的相关计算 按要求回答下列问题。
(1)标出图中的底和高。
(2)请在三角形图中再画出一组高,并进行标注。
总结:①底和高要一一对应;②画高的方法:过直线外的一点,画已知底边的( )即为高。③三角形只有( )组对应的底和高;平行四边形有( )条高;梯形有( )条高。
24.3箱苹果和4箱梨共重120千克,已知每箱苹果比每箱梨重5千克。每箱苹果和每箱梨分别重多少千克?假设7箱全都是苹果,总质量比120千克重 千克;假设7箱全都是梨,总质量要比120千克轻 千克。
25.蜘蛛爬行速度是1.9千米/小时,蜗牛爬行速度是0.045千米/小时,蜘蛛爬行速度是蜗牛的 倍。(得数保留一位小数)。
四、耐心审题,巧思妙算。(共32分)
26.口算
3.6÷1.2= 0.72÷0.9= 2.6÷13= 4.8÷0.4=
4.4÷4= 0.78÷6= 7.2÷0.4= 1÷0.25=
1.4×1= 6.2-2= 0.68×1000= 25÷0.1=
63÷9= 65÷1000= 7.2÷0.8= 44.3+55.7=
27.用竖式计算下面各题。带★的要验算。
3.06×2.4= 8.6÷0.13≈(得数保留一位小数) ★0.84÷3.5=
28.脱式计算,能简算的要简算。
90÷(3.6-1.8)
17.5÷1.25÷8
0.6×99+0.6×1
2.8÷0.4×2.5
10-6.08÷3.8
6.12-1.54-3.46
29.计算下面图形中涂色部分的面积。(单位:cm)
(1)
(2)
五、仔细观察,认真操作。(共6分)
30.按要求画一画。
(1)以虚线MN为对称轴,画出图形①的轴对称图形。
(2)画出图形①先向左平移3格,再向上平移2格后的图形。
(3)画出图形②绕点O顺时针旋转90°后的图形。
(4)画出图形②放大后的图形,使放大后的图形与原图形对应线段长的比为2:1。
(5)图形③中顶点A用数对表示为(3,2),将表示图形③轮廓点数对的第一个数乘3,第二个数不变,画出得到的图形。
六、走进生活,解决问题。(共24分)
31.圆圈代表干果,用不同颜色或方式涂一涂、说一说,小刺猬和小松鼠谁吃掉的干果更多?
客厅地面的面积为31 m2,如果用边长为0. 6 m的正方形地砖铺地面,86块够吗?
从前有个农民,临死前留下遗言,要把17头牛分给三个儿子,其中大儿子分得,二儿子分得,小儿子分得,但不能把牛卖掉或杀掉。三个儿子按照老人的要求怎么也分不好。后来一位邻居顺利地帮他们把17头牛分完了,你知道是怎么分的吗?
34.某地研究的高产技术使得新型小麦的产量可以达到每公顷9300千克,如果在如图所示的区域内种植该新型小麦,一共可以收获多少千克小麦 (单位:米)
35.阳春三月正是踏青好时节,冬冬旅行社推出“西游洞风景区一日 游”的两种价格方案。
(1)小红和小华约上几个朋友,连同家人计划参加“西游洞风景区一 日游”,他们的计划中有成人 5 人,儿童 8 人,选哪种方案合算?
(2)实际出发时,在计划的基础上增加了2名成人,此时选哪种方案合算?
答案解析部分
1.C
解:90×=15(页)
15+1=16(页)
故答案为:C。
明明第一天看的页数=这本书的页数×明明第一天看的分率,所以第二天看起的页数就是在第一天看的基础上加1页即可。
2.B
解: 这两个图形对折后能够完全重合,是轴对称图形。
故答案为:B。
依据轴对称图形的定义判断:平面内,一个图形沿一条直线折叠,直线两旁的部分能够完全重合,这个图形就是轴对称图形;其中的这条直线就是对称轴。
3.C
解:A:2是偶数不是合数,该选项说法错误;
B:把分数约分后,分数大小不变,分数单位改变,该选项说法错误;
C:由三个连续自然数组成的三位数一定是3的倍数,该选项说法正确;
D:平行四边形不是轴对称图形,该选项说法错误。
故答案为:C。
不能被2整除的数是奇数,能被2整除的数是偶数;一个数,如果只有1和它本身两个因数,这样的数叫做质数;一个数,除了1和它本身还有别的因数,这样的数叫做合数;
一个分数的分数单位就是分母分之一;
3的倍数的特征是这个数的所有数位上的数字之和是3的倍数;
如果一个图形沿着一条直线对折,两侧的图形能够完全重合,这个图形就是轴对称图形。
4.B
奇数+奇数=偶数.
故答案为:B
奇数是不能被2整除的数,两个奇数的和一定是偶数.
5.B
把整个长方形看作单位“1”,先取整个长方形的,再从取的中取,也就是,用乘法算式:
故答案为:B
可根据分数乘法的意义,求一个数的几分之几是多少用乘法计算来确定算式。
6.C
解:A:,得出的商是有限小数,不符合题意。
B:,得出的商是有限小数,不符合题意。
C:,观察到小数点后出现了周期性的数字重复(6的循环),故商是循环小数,符合题意。
D:,得出的商是有限小数,不符合题意。
故答案为:C。
循环小数的特点是在小数点后某个位置开始出现周期性的数字重复。对于这类问题,最直接的方法是计算每个选项的具体结果,观察商是否出现循环。
7.C
解:24000÷4=6000(米)
6000×6000=36000000(平方米)
36000000平方米=36平方千米
故答案为:C。
正方形的周长÷4=正方形的边长,正方形的边长×正方形的边长=正方形的面积;1平方千米=1000000平方米,把高级单位换算成低级单位要乘进率,把低级单位换算成高级单位要除以进率。
8.B
解:A:320有因数2和5;
B:540既有因数2,又有因数3,同时又有因数5;
C:405有因数3和5。
故答案为:B。
同时有因数2、3、5的数的个位数字一定是0,且各个数位上数字之和是3的倍数。
9.B
解:A:玩“石头、剪刀、布”的游戏,由于石头赢剪刀,剪刀赢布,布赢石头,形成一个循环,每种出拳方式赢的概率都是,因此小明和小华先走的概率都是 ,游戏规则公平。
B:同时抛2枚硬币,有正正、正反、反正、反反4种结果,其中只有正正1种结果是两枚硬币的数字面都朝上,其余3种情况小华先走,所以小明先走的概率是,小华先走的概率是,游戏规则不公平;
C:掷骰子,点数大于3(即4、5、6)有3种情况,小明先走;点数小于4(即1、2、3)有3种情况,小华先走。小明和小华先走的概率都是,游戏规则公平;
D:红球、黄球各3个,放入袋中,每次摸一个,然后放回。摸到红球小明先走,摸到黄球小华先走。因为红球和黄球的数量相同,所以小明和小华先走的概率都是 ,游戏规则公平。
故答案为:B。
要判断这些决定谁先走的游戏规则是否公平,需要考察每种情况下小明和小华先走的概率是否相等。如果概率相等,则游戏规则是公平的;反之,则是不公平的。
10.正确
循环小数一定是无限小数,无限小数不一定是循环小数,此题说法正确.
故答案为:正确.
小数可以分成有限小数和无限小数,小数部分的数位是有限的小数,叫做有限小数;小数部分的数位是无限的小数,叫做无限小数;无限小数分为循环小数和无限不循环小数,循环小数一定是无限小数,无限小数不一定是循环小数,据此判断.
11.错误
解:2是偶数,也是质数。
故答案为:错误。
;除了1和本身外还有其它因数的数是合数;只有1和本身两个因数的数是质数;2既是偶数,也是质数。
12.正确
解:如图,假设正方形的边长是1,
3÷1=3,这个长方形的面积是正方形面积的3倍,
长方形的周长(3+1)×2=8(厘米),正方形的周长1×4=4(厘米)
8÷4=2,周长是正方形周长的2倍,原题说法正确。
故答案为:正确。
(长+宽)×2=长方形的周长;长×宽=长方形的面积;正方形的边长×4=正方形的周长;正方形的边长×边长=正方形的面积。
13.正确
解:把一个长方形木框架拉成平行四边形,周长不变,面积变小了,说法正确。
故答案为:正确。
一个长方形框架拉成平行四边形,四条边的边长不变则周长不变;再拉的过程中,底不变,高减小,根据平行四边形的面积=底×高即可得出答案。
14.错误
解:抛硬币10次,正面朝上和反面朝上的次数不是确定的事件,原题说法错误。
故答案为:错误。
抛硬币的可能性是正面朝上和方面朝上,但是出现的次数是不确定的,据此判断。
15.正确
解:把一个平行四边形框架拉成一个长方形,这个长方形的周长与原来平行四边形的周长相等,说法正确。
故答案为:正确。
把一个平行四边形框架拉成一个长方形,只是改变了图形的形状,没有改变原图形四条边的长度,所以这个长方形的周长与原来平行四边形的周长相等。
16.;7;3
解:点A=,它的分数单位是;
2-=,再添上3个这样的分数单位就是最小的质数。
故答案为:;7;3。
最小的质数是2,分数中的分母表示把单位“1”平均分的份数,分子表示取的份数,分子是几,就表示有几个这样的分数单位。
17.6
解:4÷2=2(个),2×3=6(个),所以可以摆出6个“十”字。
故答案为:6。
一个“口”字有4根小棒,一个“十”字有2根小棒,所以一个“口”字可以摆4÷2=2(个)“十”字,所以一共可以摆“十”字的个数=“口”字的个数×一个“口”字可以摆“十”字的的个数。
18.;4;14
解:的分数单位就是,它有4个这样的分数单位;
最小的质数是2,2=,有18个这样的分数单位;
18-4=14(个);
故答案为:;4;14。
一个分数的分母是几,它的分数单位就是几分之一;分子是几就有几个这样的分数单位;
表示把单位“1”平均分成9份,每份是,根据分数单位的定义,它的分数单位就是;分子是4,所以它有4个这样的分数单位 ;
最小的质数是2,把2化成分母是9的分数得,有18个这样的分数单位,因此再加上18-4=14(个) 这样的分数单位就是最小的质数 。
19.48;36
解:120×=48(米)
42÷=36(吨)
故答案为:48,36。
求一个数的几分之几是多少,利用分数乘法计算即可;已知一个数的几分之几是a,只需用a除以分数,即可求出这个数。
20.;;;
解:涂色部分用分数表示依次是:;;;。
故答案为:;;;。
分数中的分母表示把单位“1”平均分的份数,分子表示取的份数,涂色部分占几份,分子就是几。
21.=;=;>
解:0.23的小数点向右移动一位变成2.3,0.04的小数点向右移动一位变成0.4,商不变,0.23÷0.04=2.3÷0.4;
=1,=1,=;
因为4÷6=0.66……,0.667>0.66……,所以0.667>4÷6。
故答案为:=;=;>。
商不变的规律:在除法里,被除数和除数同时扩大或者同时缩小相同的倍数,商不变;
分子和分母相同的分数,可以写成整数1;
比较小数与除法的关系,先算出除法的商,再比较小数的大小,先看它们的整数部分,整数部分大的那个数就大;整数部分相同的,十分位上的数大的那个数就大;十分位上的数也相同的,百分位上的数大的那个数就大……。
22.15;32;0.375
解:40×=15;12÷=32;=3÷8=0.375。
故答案为:15;32;0.375。
被除数=除数×商;分母=分子÷分数值;分数化小数:用分子除以分母,商写成小数的形式。
23.(1)
(2)垂线,3,无数,无数
24.20;15
解:(120+20)÷7
=140÷7
=20(千克)
(120-15)÷7
=105÷7
=15(千克)
故答案为:20;15。
每箱苹果比每箱梨重5千克 , 假设7箱全都是苹果 ,则总质量为(120+20)=140(千克),那么总质量比120千克重140-120=20(千克); 假设7箱全都是梨,则总质量为(120-15)=105(千克),那么总质量比120千克轻120-105=15(千克)。
25.42.2
解:1.9÷0.045≈42.2。
故答案为:42.2。
蜘蛛爬行速度是蜗牛的倍数=蜘蛛爬行的速度÷蜗牛爬行的速度。
26.
3.6÷1.2=3 0.72÷0.9=0.8 2.6÷13=0.2 4.8÷0.4=12
4.4÷4=1.1 0.78÷6=0.13 7.2÷0.4=18 1÷0.25=4
1.4×1=1.4 6.2-2=4.2 0.68×1000=680 25÷0.1=250
63÷9=7 65÷1000=0.065 7.2÷0.8=9 44.3+55.7=100
除数是整数的小数除法计算法则:先按照整数除法的法则去除,商的小数点要和被除数的小数点对齐;如果除到被除数的末尾仍有余数,就在余数后面添“0”,再继续除;
除数是小数的除法计算法则:先移动除数的小数点,使它变成整数,除数的小数点向右移动几位,被除数的小数点也向右移动几位(位数不够的补“0”),然后按照除数是整数的除法法则进行计算;
一个数乘10、100、1000……直接把它的小数点向右移动一位、两位、三位……;
一个数除以10、100、1000……,直接把它的小数点向左移动一位、两位、三位……;
计算小数加减法时,先把小数点对齐,也就是相同数位对齐,然后再按照整数加减法的计算法则进行计算。
27.7.344;66.2;0.24
28.解: 90÷(3.6-1.8)
=90÷1.8
=5
17.5÷1.25÷8
=17.5÷(1.25×8)
=17.5÷10
=1.75
0.6×99+0.6×1
=0.6×(99+1)
=0.6×100
=60
2.8÷0.4×2.5
=7×2.5
=17.5
10-6.08÷3.8
=10-1.6
=8.4
6.12-1.54-3.46
=6.12-(1.54+3.46)
=6.12-5
=1.12
第一题:根据四则混合运算顺序进行计算。
第二题:根据连续除以两个数等于除以这两个数的积进行简便计算
第三题:根据乘法分配律进行简便计算。
第四题:按照乘除法计算顺序进行计算。
第五题:根据四则混合运算顺序进行计算。
第六题:根据连续减去两个数等于减去这两个数的和进行简便计算。
29.(1)解:如图,三角形的面积
梯形的面积=(3+10-2-2)×(11-6)÷2=22.5(cm2),
所以涂色部分的面积=S三角形-S梯形=55-22.5=32.5(cm2)。
(2)解:如图,将涂色部分看作是三角形与平行四边形的组合,
三角形的面积
平行四边形的面积
所以涂色部分的面积
(1)本题要求解的是涂色部分的面积,通过题目描述和计算公式,可以看出需要先分别计算出三角形和梯形的面积,然后用三角形的面积减去梯形的面积,从而得到涂色部分的面积。
(2)本题要求求解由三角形和平行四边形组合而成的涂色部分的面积。根据题目给出的信息,首先计算三角形的面积,再计算平行四边形的面积,最后将两者相加得到涂色部分的总面积。
30.(1)解:
(2)解:
(3)解:
(4)解:
(5)解:
(1)补全轴对称图形,先过这个图形的关键点作对称轴的垂线,然后数出关键点到对称轴的格子数,并在另一边相同格子数的位置作上标记,最后把这些标记连接起来即可;
(2)作平移后的图形,先把关键点平移相同的格子数,然后把这些关键点连接起来即可;
(3)绕图形上一点顺时针旋转一定的度数,先把这个点连接的边顺时针旋转相同的度数,然后把剩下的边连接起来即可;
(4)把图形按照2:1放大,就是把这个图形的每条边都扩大2倍;
(5)数对中第一个数是几,表示这个点在第几列,第二个数是几,表示这个点在第几行。
31.解:12÷3=4(个)
12÷2=6(个)
答:小刺猬吃掉4个干果,小松鼠吃掉6个干果,故小松鼠吃掉的干果更多。
小刺猬、小松鼠分别吃松果的个数=松果的总个数÷各自分率的分母×分子,然后再比较大小。
32.解:0. 6×0. 6×86
=0. 36×86
=30. 96(m2)
30.96<31
答:86块不够。
用每块地砖的面积乘86求出地砖的总面积,然后与客厅面积比较后判断地砖够不够即可。
33.解:17头牛再借1头共18头,
大儿子分得:18×=9(头)
二儿子分得:18×=6(头)
小儿子分得:18×=2(头)
三个儿子一共分了:9+6+2=17(头)
剩下的一头还回去即可
答:大儿子分得9头牛,二儿子分得6头牛,小儿子分得2头牛。
因为2、3、9的最小公倍数是18,所以再借一头就可以直接分了;牛的总头数×= 大儿子分的头数,牛的总头数×=二儿子分的头数,牛的总头数×=小儿子分的头数,分完还余下一头,再还回去就可以了。
34.解:梯形的面积:
(20+35)×50÷2=1375(平方米)
三角形的面积:
24×40÷2=480(平方米)
平行四边形的面积:
12×35=420(平方米)
种植区域的面积:
1375+480+420=2275(平方米)=0.2275(公顷),
0.2275×9300=2115.75(千克)。
答:一共可以收获2115.75千克小麦。
观察图形,可知,小麦种植区域的面积等于以上底为20,下底为35,高为50的梯形的面积加上以底为40,高为24的三角形面积再加上以高为12,底为35的平行四边形的面积,利用梯形的面积公式:S=(上底+下底)×高÷2,三角形的满级公式:S=底×高÷2,平行四边形的面积公式:S=ah,然后代入数据即可,再将平方米化为公顷,最后再将面积乘以每公顷的产量,即可求解
35.(1)解:方案 1:
5×120+8×50
=600+400
=1000(元)
方案 2:
(5+8)×80
=13×80
=1040(元)
1000<1040。
答:选择方案1合算。
(2)解:方案 1:
(2+5)×120+8×50
=840+400
=1240(元)
方案 2:
(2+5+8)×80
=15×80
=1200(元)
1200<1240
答:选择方案2合算。
方案1:成人每人的钱数×人数+儿童每人的钱数×人数=一共需要的钱数;
方案2:总人数×每人的钱数=一共需要的钱数;
哪种方案花钱少,选哪种方案合算。
同课章节目录
