2024-2025学年北师大版八年级数学上册期末押题卷(含答案+解析)
文档属性
| 名称 | 2024-2025学年北师大版八年级数学上册期末押题卷(含答案+解析) |  | |
| 格式 | docx | ||
| 文件大小 | 555.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-09 21:15:51 | ||
图片预览



文档简介
保密★启用前
20224-2025学年八年级上册期末押题卷(北师大版)
数学
考试范围:八上全册 考试时间:100分钟 分值:120分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
一、选择题(本大题10小题,每小题3分,共30分)
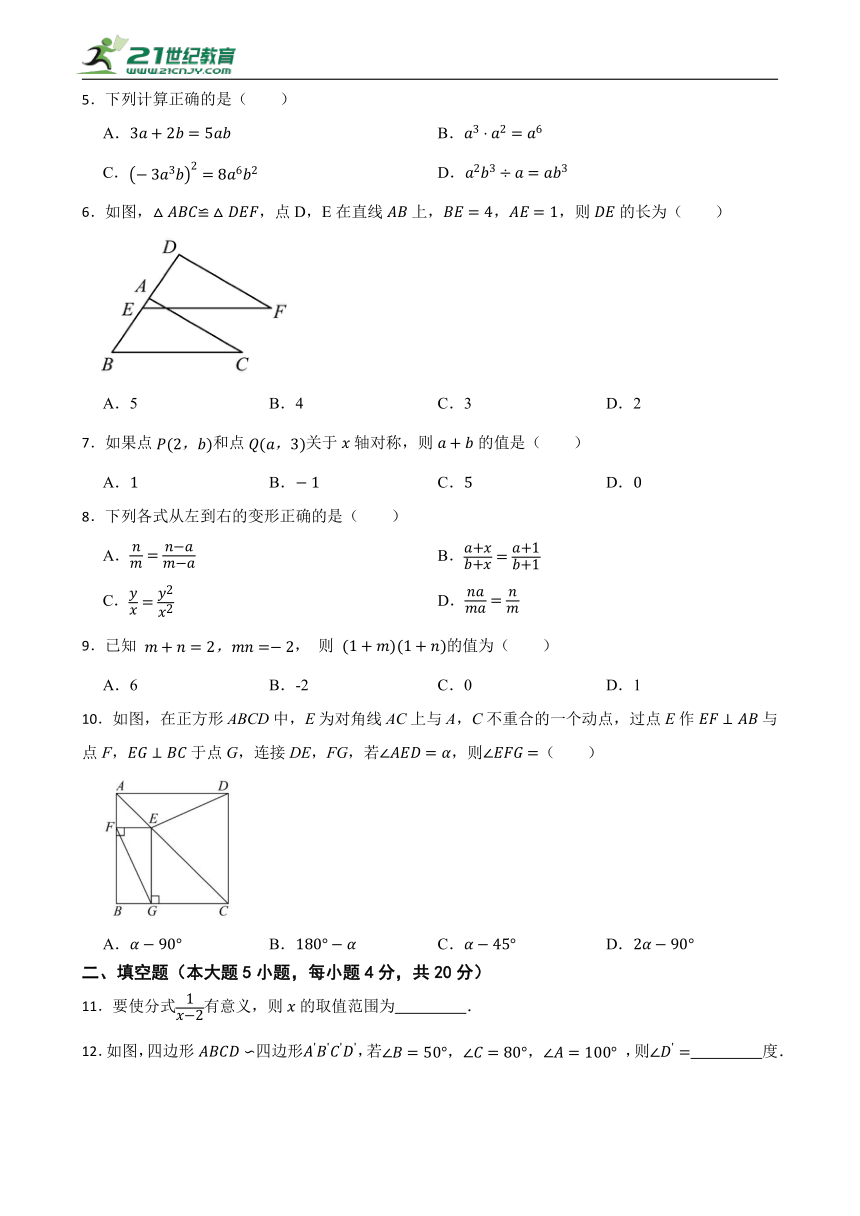
1.2024年6月25日,嫦娥六号返回器准确着陆于预定区域,工作正常,标志着探月工程嫦娥六号任务取得圆满成功,实现世界首次月球背面采样返回.下列航天领域的图标中,既是轴对称图形又是中心对称图形的是( )
A. B.
C. D.
2.若三角形的两边长分别为和,则第三边的长不可能是( )
A. B. C. D.
3.某科技公司生成的芯片采用了8纳米的工艺技术,8纳米等于0.000000008米,数据0.000000008用科学记数法表示为( )
A. B. C. D.
4.如图,将(其中,)绕点按顺时针方向旋转到的位置,使得点、、在同一条直线上,那么旋转角等于( )
A. B. C. D.
5.下列计算正确的是( )
A. B.
C. D.
6.如图,,点D,E在直线上,,,则的长为( )
A.5 B.4 C.3 D.2
7.如果点和点关于轴对称,则的值是( )
A. B. C. D.
8.下列各式从左到右的变形正确的是( )
A. B.
C. D.
9.已知 , 则 的值为( )
A.6 B.-2 C.0 D.1
10.如图,在正方形ABCD中,E为对角线AC上与A,C不重合的一个动点,过点E作与点F,于点G,连接DE,FG,若,则( )
A. B. C. D.
二、填空题(本大题5小题,每小题4分,共20分)
11.要使分式有意义,则的取值范围为 .
12.如图,四边形四边形,若 ,则 度.
13.已知,,则代数式 的值为 .
14.如图,在中,按以下步骤作图:①分别以B,C为圆心,大于的长为半径画弧,两弧相交于M,N两点;②作直线交于点D,连接.若,则的度数为 .
15.如图,点M在等边ABC的边BC上,BM=8,射线CD⊥BC垂足为点C,点P是射线CD上一动点,点N是线段AB上一动点,当MP+NP的值最小时,BN=9,则AC的长为 .
三、解答题(一)(本大题2小题,每小题5分,共10分)
16.
计算:.
化简:.
17.计算:
(1);
(2);
;
.
四、解答题(二)(本大题5小题,每小题6分,共30分)
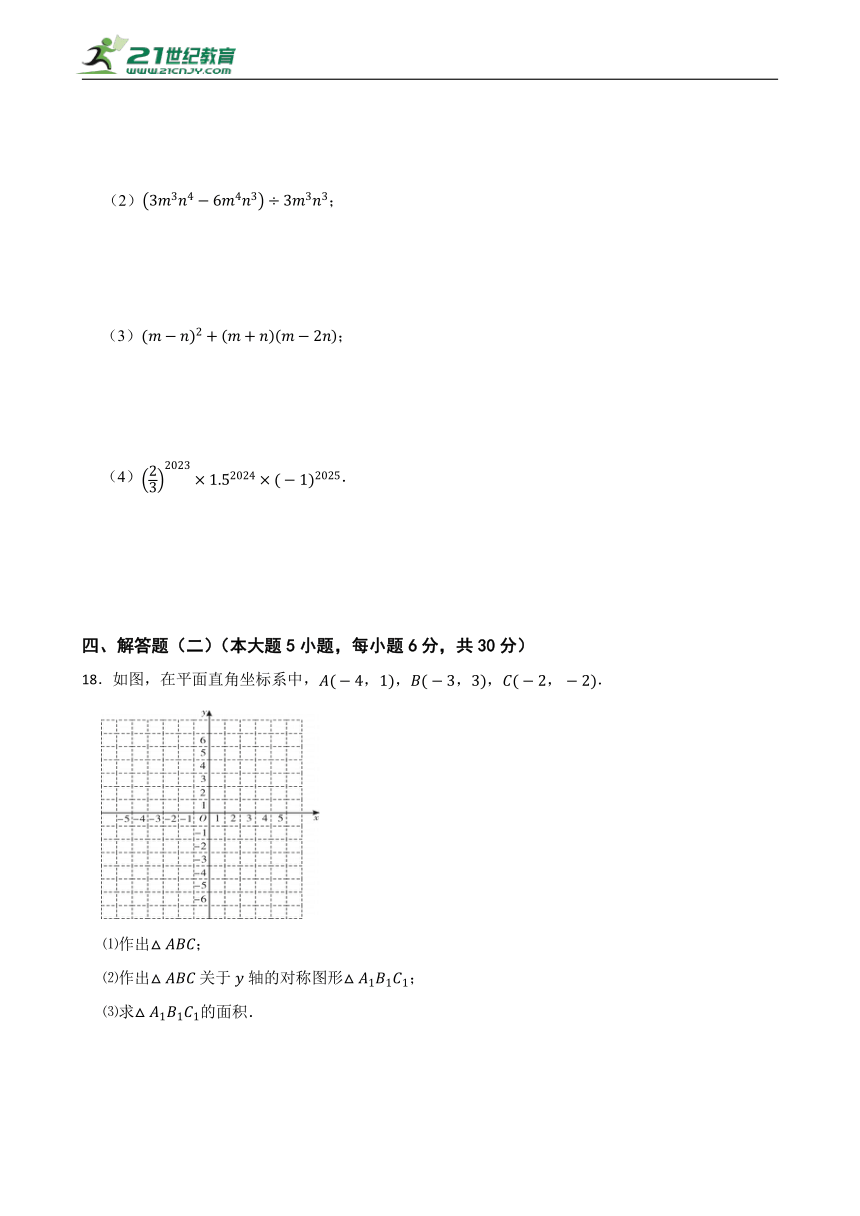
18.如图,在平面直角坐标系中,.
⑴作出;
⑵作出关于轴的对称图形;
⑶求的面积.
19.已知: 如图 和 PC 分别平分 和 过点 , 且与 AB 垂直. 求证: .
此题的延伸结论:
① ▲
② 之间的数量关系为 ▲
③ 之间的数量关系为 ▲
先化简,再求值:,其中且为正整数.
21.如图,中,,,.
(1)用尺规作图在上找一点M,使点M到和的距离相等.(不写作法,保留作图痕迹);
(2)求的长.
22. 如图,在平面直角坐标系中,点C在y轴的正半轴上,点B与点A关于y轴对称,为等边三角形,,.
(1)求点A的坐标;
(2)动点F从原点出发,以每秒1个单位长度的速度,沿x轴正方向运动,运动时间为t秒,求的面积S与t之间的关系(用含t的式子表示S).
(3)在(2)的条件下,当点F运动到点A时,有一动点E从点C出发,以每秒1个单位长度的速度,沿线段向终点B运动,当点E到达终点时,点E、F运动停止,连接交于点G,交y轴于点K,
①过点E作于点H,求线段的长;
②如图,当,时,在x轴负半轴有一点L,连接,在y轴上取一点M,,连接并延长,交于点N,若.求线段的长.
五、解答题(三)(本大题2小题,每小题9分,共18分)
23.某市对一段全长2000米的道路进行改造.为了尽量减少施工对城市交通所造成的影响,实际施工时,若每天修路比原计划提高效率,就可以提前5天完成修路任务.
(1)求修这段路计划用多少天?
(2)有甲、乙两个工程队参与修路施工,其中甲队每天可修路120米,乙队每天可修路80米,若每天只安排一个工程队施工,在保证至少提前5天完成修路任务的前提下,甲工程队至少要修路多少天?
24.我们知道,图形是一种重要的数学语言,它直观形象,能有效地表现一些代数中的数量关系,反之运用代数思想也能巧妙的解决一些图形问题.现有长与宽分别为a、b的小长方形若干个,用两个这样的小长方形拼成如图①的图形.
(1)请用两种不同的方法表示图①中阴影部分的面积和,可以得到的等式是:________;
(2)根据(1)中的等式计算:若,求的值;
(3)如图②,点C是线段上的一点,以为边向两边作正方形,设,两正方形的面积和,直接写出图中阴影部分的面积为________.
六、解答题(四)(本大题1小题,每小题12分,共12分)
25.如图1,在正方形中,O是对角线的交点,P是线段上任一点(不与点A,O重合),过点P作,交边于点E.
(1) 的度数为 .
(2)求证:.
(3)如图2,若正方形的边长为4,过点E作于点F,在点P运动的过程中,的长度是否发生变化?若不发生变化,直接写出这个不变的值;若发生变化,请说明理由.
答案解析部分
1.B
2.A
解:设第三边的长为,
∵ 三角形的两边长分别为和,
∴,
∴,
故答案为:A.
设第三边的长为,根据三角形三边关系:两边之和大于第三边,两边之差小于第三边,确定x的取值范围,即可得到答案.
3.D
4.C
5.D
6.A
解:∵点D,E在直线AB上,且BE=4,AE=1,
∴AB=AE+BE=5,
∵,
∴DE=AB=5.
故答案为:A.
先根据AB=AE+BE算出AB的长,然后根据全等三角形的对应边相等得DE=AB=5.
7.B
解:∵点和点关于轴对称,
∴a=2,b=-3,
∴a+b=-1,
故答案为:B
根据关于x轴对称的点坐标特征(横坐标不变,纵坐标变成相反数)即可求出a和b,进而即可求解。
8.D
9.D
解:.
故答案为:1.
先去括号,后代入条件即可求值.
10.C
解:如图所示,延长交于点H,连接BE,如图:
∵四边形ABCD是正方形,
∴∠ABC=90°.
过点E作与点F,于点G,
∴四边形是矩形
∴,
易证,
∴
∵四边形是正方形,
∴
∴
∴,是等腰直角三角形
∴
∵
∴四边形是正方形
∴
∴在和中
∴
∴
∵
∴
∴.
故答案为:C.
延长交于点H,由题意得四边形是矩形,得到,,然后由正方形的性质证明出,是等腰直角三角形,得到,根据全等三角形的判定证明,得到,然后利用角度的等量代换即可求解.
11.
12.130
13.
14.
15.13
16.(1)解:
.
(2)解:
;
(1)先计算零指数幂,负整数指数幂和开平方运算,再进行有理数的加减运算;
(2)先进行多项式÷单项式的运算,再合并同类项.
17.(1)
(2)
(3)
(4)
18.解:如图:
⑴即为所求;
⑵即为所求;
⑶
(1)由A、B、C的坐标先描点,再连线即可;
(2)分别作出点A、B、C关于y轴对称点A1、B1、C1,再顺次连接即可;
(3)利用割补法求出三角形的面积即可.
19.证明: 如图,过点 作 于点 .
,
.
和 分别平分 和 ,
.
.
此题的延伸结论:
①
②
③
解:①∵AB∥CD
∴∠ABC+∠BCD=180°
∵PB和PC平分∠ABC和∠DCB
∴
∴
∴∠BPC=180°-90°=90°
故答案为:90°
②∵∠ABP=∠PBH,∠BAP=∠BHP=90°,PB=PB
∴△PAB≌△PHB(AAS)
同理可得:△PCD≌△PCH
∴BH=AB,CH=CD
∴BH+CH=AB+CD
∴BC=AB+CD
故答案为:BC=AB+CD
③∵△PAB≌△PHB,△PCD≌△PCH
∴
∴
故答案为:
过点 作 于点 ,根据直线平行性质可得,再根据角平分线性质可得,则PA=PD,即可求出答案.
①根据直线平行性质可得∠ABC+∠BCD=180°,再根据角平分线定义可得,则,再根据三角形内角和定理即可求出答案.
②根据全等三角形判定定理可得△PAB≌△PHB(AAS),同理可得:△PCD≌△PCH,则BH=AB,CH=CD,再根据边之间的关系即可求出答案.
③根据全等三角形性质可得,再根据三角形面积即可求出答案.
20.,x=2时,原式=6.
21.(1)解:作的角平分线交于点M,则点M即为所求;
(2)解:过点M作于点D,
∵在中,,,,
∴,
∴,
∴,
∵平分,
∴,
∵,,
∴
在和中,
,
∴,
∴,
∴
设,
∴,
解得:,
∴.
(1)由角平分线上的点到两边距离相等联想到作角平分线;
(2)由角平分线上的点的性质可将求MA的问题转化为求MD的问题,这样可以利用到sin∠ACB的值.
22.(1)解:解:设AC为x,
∵为等边三角形,点B与点A关于y轴对称,
∴OA=,
∵,∴.
∵,
∴,解得x=6,
∴OA=3.
∴;
(2)解:由题意可知,,
当时,点在线段上,则,
∴的面积;
当时,点在线段的延长线上,则,
∴的面积;
综上,当时,;当时,
(3)解:①当点运动到点时,有一动点从点出发,以每秒1个单位长度的速度,
∴,
∵是等边三角形,
∴,,
过点作,则,,,
∴是等边三角形,则,
又∵,
∴,
∴,
∵,
∴,
则,
∴;
②当时,即,可得:,
∴,
∵,,
∴,
∴,
∵,
∴,
在上取,则,
过点作,交延长线于,则,
设,则,
∵,则,
∴,则,
由三角形内角和可得,
∴,则,
∴,
又∵,
∴,
∴,
又∵,
由三角形内角和可得,
∴,则,
∵,,
∴.
(1)根据C点的坐标,设AC为x,则可得OA=,利用勾股定理可求得x,从而可得A点的坐标;
(2)分“与”两种情况讨论,分别求出的面积S与t之间的关系.
(3)①先利用AAS证明,再根据全等三角形的性质,得出,再说明CH=TH,接着求出AC与GH的关系,求出GH的长;
②过点作,交延长线于,根据, 得出t的方程求出t,利用SAS说明,接着说明MN=KM,结合,,求出MN的长.
23.(1)25
(2)10
24.(1)
(2)
(3)12
25.(1)45°
(2)证明:如图1,过点P作MN∥AD,交AB于点M,交CD于点N.
则BM=CN,
∵PB⊥PE,
∴∠BPE= ,
∴∠MPB+∠NPE= .
∵四边形ABCD是正方形,
∴∠BAD=∠D= ,∠PCN= ,
∵AD∥MN,
∴∠BMP=∠BAD=∠PNE=∠D= ,
∴∠MPB+∠MBP= ,
∴∠NPE=∠MBP.
在Rt△PNC中,∠PCN= ,
∴△PNC是等腰直角三角形,
∴PN=CN,
∴BM=CN=PN,
∴△BMP≌△PNE(ASA),
∴PB=PE;
(3)解:PF的长不发生变化,为定值2 .
(1)解:∵在正方形 中,AC是对角线,
∴ = ,
故答案为: ;
解:(3)在P点运动的过程中,PF的长度不发生变化.理由如下:
如图2,连接OB.
∵四边形ABCD是边长为4的正方形,
∴AB=CB=4,
∵点O是AC的中点,
∴OB⊥AC,
∴∠AOB= ,
∴∠AOB=∠EFP= ,
∴∠OBP+∠BPO= .
∴∠BPE= ,
∴∠BPO+∠FPE= ,
∴∠OBP=∠FPE.
由(1)得:PB=PE,
∴△OBP≌△FPE(AAS),
∴PF=OB.
∵△ABO是等腰直角三角形,
∴OB= AB=2 ,
∴PF=2 ,
即PF的长不发生变化,为定值2 .
(1)由正方形的性质即可求解;
(2)过点P作MN∥AD,交AB于点M,交CD于点N,证明△BMP≌△PNE(ASA),可得PB=PE;
(3)在P点运动的过程中,PF的长度不发生变化.理由:连接OB,证明△OBP≌△FPE(AAS),可得PF=OB.由△ABO是等腰直角三角形,可得OB= AB=2 ,即得PF的长.
20224-2025学年八年级上册期末押题卷(北师大版)
数学
考试范围:八上全册 考试时间:100分钟 分值:120分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
一、选择题(本大题10小题,每小题3分,共30分)
1.2024年6月25日,嫦娥六号返回器准确着陆于预定区域,工作正常,标志着探月工程嫦娥六号任务取得圆满成功,实现世界首次月球背面采样返回.下列航天领域的图标中,既是轴对称图形又是中心对称图形的是( )
A. B.
C. D.
2.若三角形的两边长分别为和,则第三边的长不可能是( )
A. B. C. D.
3.某科技公司生成的芯片采用了8纳米的工艺技术,8纳米等于0.000000008米,数据0.000000008用科学记数法表示为( )
A. B. C. D.
4.如图,将(其中,)绕点按顺时针方向旋转到的位置,使得点、、在同一条直线上,那么旋转角等于( )
A. B. C. D.
5.下列计算正确的是( )
A. B.
C. D.
6.如图,,点D,E在直线上,,,则的长为( )
A.5 B.4 C.3 D.2
7.如果点和点关于轴对称,则的值是( )
A. B. C. D.
8.下列各式从左到右的变形正确的是( )
A. B.
C. D.
9.已知 , 则 的值为( )
A.6 B.-2 C.0 D.1
10.如图,在正方形ABCD中,E为对角线AC上与A,C不重合的一个动点,过点E作与点F,于点G,连接DE,FG,若,则( )
A. B. C. D.
二、填空题(本大题5小题,每小题4分,共20分)
11.要使分式有意义,则的取值范围为 .
12.如图,四边形四边形,若 ,则 度.
13.已知,,则代数式 的值为 .
14.如图,在中,按以下步骤作图:①分别以B,C为圆心,大于的长为半径画弧,两弧相交于M,N两点;②作直线交于点D,连接.若,则的度数为 .
15.如图,点M在等边ABC的边BC上,BM=8,射线CD⊥BC垂足为点C,点P是射线CD上一动点,点N是线段AB上一动点,当MP+NP的值最小时,BN=9,则AC的长为 .
三、解答题(一)(本大题2小题,每小题5分,共10分)
16.
计算:.
化简:.
17.计算:
(1);
(2);
;
.
四、解答题(二)(本大题5小题,每小题6分,共30分)
18.如图,在平面直角坐标系中,.
⑴作出;
⑵作出关于轴的对称图形;
⑶求的面积.
19.已知: 如图 和 PC 分别平分 和 过点 , 且与 AB 垂直. 求证: .
此题的延伸结论:
① ▲
② 之间的数量关系为 ▲
③ 之间的数量关系为 ▲
先化简,再求值:,其中且为正整数.
21.如图,中,,,.
(1)用尺规作图在上找一点M,使点M到和的距离相等.(不写作法,保留作图痕迹);
(2)求的长.
22. 如图,在平面直角坐标系中,点C在y轴的正半轴上,点B与点A关于y轴对称,为等边三角形,,.
(1)求点A的坐标;
(2)动点F从原点出发,以每秒1个单位长度的速度,沿x轴正方向运动,运动时间为t秒,求的面积S与t之间的关系(用含t的式子表示S).
(3)在(2)的条件下,当点F运动到点A时,有一动点E从点C出发,以每秒1个单位长度的速度,沿线段向终点B运动,当点E到达终点时,点E、F运动停止,连接交于点G,交y轴于点K,
①过点E作于点H,求线段的长;
②如图,当,时,在x轴负半轴有一点L,连接,在y轴上取一点M,,连接并延长,交于点N,若.求线段的长.
五、解答题(三)(本大题2小题,每小题9分,共18分)
23.某市对一段全长2000米的道路进行改造.为了尽量减少施工对城市交通所造成的影响,实际施工时,若每天修路比原计划提高效率,就可以提前5天完成修路任务.
(1)求修这段路计划用多少天?
(2)有甲、乙两个工程队参与修路施工,其中甲队每天可修路120米,乙队每天可修路80米,若每天只安排一个工程队施工,在保证至少提前5天完成修路任务的前提下,甲工程队至少要修路多少天?
24.我们知道,图形是一种重要的数学语言,它直观形象,能有效地表现一些代数中的数量关系,反之运用代数思想也能巧妙的解决一些图形问题.现有长与宽分别为a、b的小长方形若干个,用两个这样的小长方形拼成如图①的图形.
(1)请用两种不同的方法表示图①中阴影部分的面积和,可以得到的等式是:________;
(2)根据(1)中的等式计算:若,求的值;
(3)如图②,点C是线段上的一点,以为边向两边作正方形,设,两正方形的面积和,直接写出图中阴影部分的面积为________.
六、解答题(四)(本大题1小题,每小题12分,共12分)
25.如图1,在正方形中,O是对角线的交点,P是线段上任一点(不与点A,O重合),过点P作,交边于点E.
(1) 的度数为 .
(2)求证:.
(3)如图2,若正方形的边长为4,过点E作于点F,在点P运动的过程中,的长度是否发生变化?若不发生变化,直接写出这个不变的值;若发生变化,请说明理由.
答案解析部分
1.B
2.A
解:设第三边的长为,
∵ 三角形的两边长分别为和,
∴,
∴,
故答案为:A.
设第三边的长为,根据三角形三边关系:两边之和大于第三边,两边之差小于第三边,确定x的取值范围,即可得到答案.
3.D
4.C
5.D
6.A
解:∵点D,E在直线AB上,且BE=4,AE=1,
∴AB=AE+BE=5,
∵,
∴DE=AB=5.
故答案为:A.
先根据AB=AE+BE算出AB的长,然后根据全等三角形的对应边相等得DE=AB=5.
7.B
解:∵点和点关于轴对称,
∴a=2,b=-3,
∴a+b=-1,
故答案为:B
根据关于x轴对称的点坐标特征(横坐标不变,纵坐标变成相反数)即可求出a和b,进而即可求解。
8.D
9.D
解:.
故答案为:1.
先去括号,后代入条件即可求值.
10.C
解:如图所示,延长交于点H,连接BE,如图:
∵四边形ABCD是正方形,
∴∠ABC=90°.
过点E作与点F,于点G,
∴四边形是矩形
∴,
易证,
∴
∵四边形是正方形,
∴
∴
∴,是等腰直角三角形
∴
∵
∴四边形是正方形
∴
∴在和中
∴
∴
∵
∴
∴.
故答案为:C.
延长交于点H,由题意得四边形是矩形,得到,,然后由正方形的性质证明出,是等腰直角三角形,得到,根据全等三角形的判定证明,得到,然后利用角度的等量代换即可求解.
11.
12.130
13.
14.
15.13
16.(1)解:
.
(2)解:
;
(1)先计算零指数幂,负整数指数幂和开平方运算,再进行有理数的加减运算;
(2)先进行多项式÷单项式的运算,再合并同类项.
17.(1)
(2)
(3)
(4)
18.解:如图:
⑴即为所求;
⑵即为所求;
⑶
(1)由A、B、C的坐标先描点,再连线即可;
(2)分别作出点A、B、C关于y轴对称点A1、B1、C1,再顺次连接即可;
(3)利用割补法求出三角形的面积即可.
19.证明: 如图,过点 作 于点 .
,
.
和 分别平分 和 ,
.
.
此题的延伸结论:
①
②
③
解:①∵AB∥CD
∴∠ABC+∠BCD=180°
∵PB和PC平分∠ABC和∠DCB
∴
∴
∴∠BPC=180°-90°=90°
故答案为:90°
②∵∠ABP=∠PBH,∠BAP=∠BHP=90°,PB=PB
∴△PAB≌△PHB(AAS)
同理可得:△PCD≌△PCH
∴BH=AB,CH=CD
∴BH+CH=AB+CD
∴BC=AB+CD
故答案为:BC=AB+CD
③∵△PAB≌△PHB,△PCD≌△PCH
∴
∴
故答案为:
过点 作 于点 ,根据直线平行性质可得,再根据角平分线性质可得,则PA=PD,即可求出答案.
①根据直线平行性质可得∠ABC+∠BCD=180°,再根据角平分线定义可得,则,再根据三角形内角和定理即可求出答案.
②根据全等三角形判定定理可得△PAB≌△PHB(AAS),同理可得:△PCD≌△PCH,则BH=AB,CH=CD,再根据边之间的关系即可求出答案.
③根据全等三角形性质可得,再根据三角形面积即可求出答案.
20.,x=2时,原式=6.
21.(1)解:作的角平分线交于点M,则点M即为所求;
(2)解:过点M作于点D,
∵在中,,,,
∴,
∴,
∴,
∵平分,
∴,
∵,,
∴
在和中,
,
∴,
∴,
∴
设,
∴,
解得:,
∴.
(1)由角平分线上的点到两边距离相等联想到作角平分线;
(2)由角平分线上的点的性质可将求MA的问题转化为求MD的问题,这样可以利用到sin∠ACB的值.
22.(1)解:解:设AC为x,
∵为等边三角形,点B与点A关于y轴对称,
∴OA=,
∵,∴.
∵,
∴,解得x=6,
∴OA=3.
∴;
(2)解:由题意可知,,
当时,点在线段上,则,
∴的面积;
当时,点在线段的延长线上,则,
∴的面积;
综上,当时,;当时,
(3)解:①当点运动到点时,有一动点从点出发,以每秒1个单位长度的速度,
∴,
∵是等边三角形,
∴,,
过点作,则,,,
∴是等边三角形,则,
又∵,
∴,
∴,
∵,
∴,
则,
∴;
②当时,即,可得:,
∴,
∵,,
∴,
∴,
∵,
∴,
在上取,则,
过点作,交延长线于,则,
设,则,
∵,则,
∴,则,
由三角形内角和可得,
∴,则,
∴,
又∵,
∴,
∴,
又∵,
由三角形内角和可得,
∴,则,
∵,,
∴.
(1)根据C点的坐标,设AC为x,则可得OA=,利用勾股定理可求得x,从而可得A点的坐标;
(2)分“与”两种情况讨论,分别求出的面积S与t之间的关系.
(3)①先利用AAS证明,再根据全等三角形的性质,得出,再说明CH=TH,接着求出AC与GH的关系,求出GH的长;
②过点作,交延长线于,根据, 得出t的方程求出t,利用SAS说明,接着说明MN=KM,结合,,求出MN的长.
23.(1)25
(2)10
24.(1)
(2)
(3)12
25.(1)45°
(2)证明:如图1,过点P作MN∥AD,交AB于点M,交CD于点N.
则BM=CN,
∵PB⊥PE,
∴∠BPE= ,
∴∠MPB+∠NPE= .
∵四边形ABCD是正方形,
∴∠BAD=∠D= ,∠PCN= ,
∵AD∥MN,
∴∠BMP=∠BAD=∠PNE=∠D= ,
∴∠MPB+∠MBP= ,
∴∠NPE=∠MBP.
在Rt△PNC中,∠PCN= ,
∴△PNC是等腰直角三角形,
∴PN=CN,
∴BM=CN=PN,
∴△BMP≌△PNE(ASA),
∴PB=PE;
(3)解:PF的长不发生变化,为定值2 .
(1)解:∵在正方形 中,AC是对角线,
∴ = ,
故答案为: ;
解:(3)在P点运动的过程中,PF的长度不发生变化.理由如下:
如图2,连接OB.
∵四边形ABCD是边长为4的正方形,
∴AB=CB=4,
∵点O是AC的中点,
∴OB⊥AC,
∴∠AOB= ,
∴∠AOB=∠EFP= ,
∴∠OBP+∠BPO= .
∴∠BPE= ,
∴∠BPO+∠FPE= ,
∴∠OBP=∠FPE.
由(1)得:PB=PE,
∴△OBP≌△FPE(AAS),
∴PF=OB.
∵△ABO是等腰直角三角形,
∴OB= AB=2 ,
∴PF=2 ,
即PF的长不发生变化,为定值2 .
(1)由正方形的性质即可求解;
(2)过点P作MN∥AD,交AB于点M,交CD于点N,证明△BMP≌△PNE(ASA),可得PB=PE;
(3)在P点运动的过程中,PF的长度不发生变化.理由:连接OB,证明△OBP≌△FPE(AAS),可得PF=OB.由△ABO是等腰直角三角形,可得OB= AB=2 ,即得PF的长.
同课章节目录
