2024-2025学年人教版八年级数学上册期末押题卷(含答案+解析)
文档属性
| 名称 | 2024-2025学年人教版八年级数学上册期末押题卷(含答案+解析) |  | |
| 格式 | docx | ||
| 文件大小 | 402.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-09 21:14:59 | ||
图片预览




文档简介
保密★启用前
20224-2025学年八年级上册期末押题卷(人教版)
数学
考试范围:七上全册 考试时间:100分钟
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
一、单选题
1.如图,在一次活动中,位于处的班准备前往相距的处与班会合,那么用方向和距离描述班相对于班的位置是( )
A.南偏西,距离 B.北偏东,距离
C.南偏西,距离 D.北偏东,距离
2.在实数(不循环)、、、、、、、、中,无理数的个数为( )
A.2个 B.3个 C.4个 D.5个
3.如图,,CE平分,若,则的度数是( )
A.25° B.50° C.65° D.130°
4.如图,在平面直角坐标系中,点,,,和,,,分别在直线和轴上,,,,都是等腰直角三角形(点,,,为直角顶点),那么点的坐标是( )
A. B. C. D.
5.一次函数的图象不经过( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
6.某公司招聘员工,将笔试和面试两项测试得分按的比例确定个人的测试成绩.若张红笔试成绩为95分,面试成绩为90分,则她的测试成绩是( )
A.分 B.分 C.分 D.分
7.小丽同学带11元钱去买钢笔和笔记本(两种文具都买),钢笔每支3元,笔记本每本1元,那么钢笔能买( )
A.1支 B.1支或2支或3支
C.2支 D.2支或3支
8.已知直线y=﹣3x+m过点A(﹣1,y1)和点(﹣3,y2),则y1和y2的大小关系是( )
A.y1>y2 B.y1<y2 C.y1=y2 D.不能确定
9.我国古代数学著作《孙子算经》有“多人共车”问题:“今有三人共车,二车空;二人共车,九人步.问:人与车各几何 ”其大意如下:有若干人要坐车,如果每3人坐一辆车,那么有2辆空车;如果每2人坐一辆车,那么有9人需要步行,问人与车各多少 设共有 人, 辆车,则可列方程组为( )
A. B.
C. D.
10.如图,把正方形铁片置于平面直角坐标系中,顶点的坐标为,点在正方形铁片上,将正方形铁片绕其右下角的顶点按顺时针方向依次旋转,第一次旋转至图①位置,第二次旋转至图②位置,…则正方形铁片连续旋转次后,点的坐标为( )
A. B. C. D.
二、填空题
11.“等腰三角形两底角相等”的逆命题是 ,这个逆命题是 命题.
12. 已知关于 的方程组 的解及 都是正整数. 则: (1) 当 时,方程组的解是 ,(2) 满足条件的所有解的个数是
13.规定:用符号表示一个不大于实数的最大整数,例如:,,,按这个规定:
(1) ;(2) ;
(3)若,则的取值范围是 .
14.如图,圆柱体中底面周长是,是底面直径,高,点是上一点且,一只从点出发沿着圆柱体的侧面爬行到点,则小虫爬行的最短路程是 .
15.在平面直角坐标系中,已知,点在以为圆心,为半径的圆上运动,作点关于直线、的对称点、,则 ,DE的最小值为 .
三、解答题
16.计算
(1)
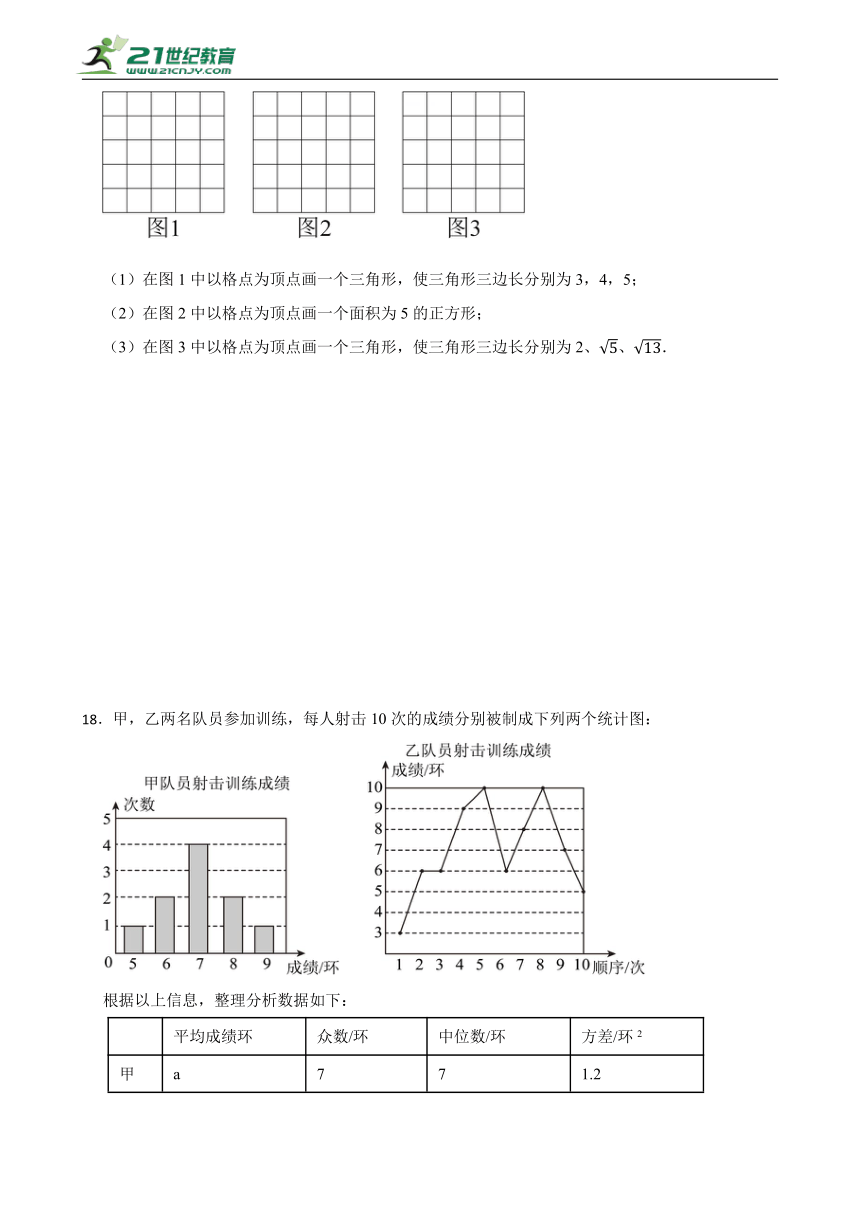
17.如图,正方形网格中的每个小正方形的边长都是1,每个小格的顶点叫做格点.
(1)在图1中以格点为顶点画一个三角形,使三角形三边长分别为3,4,5;
(2)在图2中以格点为顶点画一个面积为5的正方形;
(3)在图3中以格点为顶点画一个三角形,使三角形三边长分别为2、、.
18.甲,乙两名队员参加训练,每人射击10次的成绩分别被制成下列两个统计图:
根据以上信息,整理分析数据如下:
平均成绩环 众数/环 中位数/环 方差/环2
甲 a 7 7 1.2
乙 7 b c 4.6
(1)写出表格中a,b,c的值: , , ;
(2)根据以上统计数据,你会选择谁参加比赛,请说明理由.
19.为迎接培圣校园科技节的到来,学校科技社团欲购买甲、乙两种模型进行组装,已知3套甲模型的总价与2套乙模型的总价相等,若购买1套甲模型和2套乙模型共需80元.
(1)求甲、乙两种模型的单价各是多少元?
(2)现计划用1220元资金,在不超过预算的情况下,购买这两种模型共50套,且乙种模型的数量不少于甲种模型数量的,求两种模型共有多少种选购方案.
20.某班“数学兴趣小组”根据学习一次函数的经验,对函数的图象和性质进行了研究探究过程如下,请补充完整.
(1)自变量的取值范围是全体实数下表是与的几组对应值:
其中, ;
(2)如下图,在平面直角坐标系中,描出了以上表中各对对应值为坐标的点,并画出了函数图象的一部分,请画出该函数图象的另一部分;
(3)观察函数图象发现,该函数图象的最低点坐标是 ;
当时,随的增大而减小;当时,随的增大而 ;
(4)进一步探究,若关于的方程只有一个解,则的取值范围是 .
21.甲、乙两个工程队修筑一条公路,甲队从南向北方向修筑,乙队从北向南方向修筑甲、乙两队同时开工,乙队施工几天后因另有任务提前离开,甲队继续修筑公路当乙队任务完成后,因赶时间,乙队回来继续修筑公路,直到公路修通在修路过程中,甲、乙两队的工作效率保持不变设甲、乙两队修筑公路的长度为米,施工时间为天,与之间的函数图象如图所示.
(1)甲队每天修筑公路 米,乙队每天修筑公路 米;
(2)求乙队离开的天数;
(3) 求乙队回来后修筑公路的长度与之间的函数关系式,并写出自变量的取值范围;
(4) 求这条公路的总长度.
答案解析部分
1.D
2.C
3.D
解:,,
,,
平分,
,
.
故答案为:D.
根据平行线的性质得,,根据角平分线的定义得,代数求解即可.
4.D
5.A
6.C
7.B
解:设能买x支钢笔和y个笔记本,根据题意得:
3x+y=11,
∵x、y为正整数,
当x=1时,y=8;
当x=2时,y=5;
当x=3时,y=2;
当x=4时,y=-1(舍去).
∴钢笔能买1支或2支或3支.
故答案为:B
设能买x支钢笔和y个笔记本,根据:钢笔的费用+笔记本的费用=11元列出方程,然后求出其正整数解即可.
8.B
解:∵函数y=-3x+m中,k=-3<0,
∴y随x的增大而减小,
∵函数y=-3x+m的图象经过点A(-l,y1)和点B(-3,y2),
-3<-1,
∴y1<y2,
故答案为:B.
根据一次函数的解析式可以知道:y随x的增大而减小,利用此性质求解即可。
9.C
解:设共有 人, 辆车,则
故答案为:C
设共有 人, 辆车,根据“ 如果每3人坐一辆车,那么有2辆空车;如果每2人坐一辆车,那么有9人需要步行 ”列出方程组即可.
10.C
11.有两个角相等的三角形是等腰三角形;真
12.;6
解:(1)、解方程组 ,得,则明显可知a为6的倍数.
又∵a≤6,
∴a=6.
∴故方程的解为:;
(2)、由题干条件可知,a的取值有6、12、18、24、30、36,对应的解的个数为6个.
故答案为:6
(1)先解方程组,再根据已知求出满足条件的所有正整数a,然后将a的值代入求解即可;
(2)根据(1)x、y的表达式,结合条件求出满足条件的所有正整数a,a有多少个可能的取值,则对应多少个解.
13.1;;
(1),
,
故答案为:1.
(2),
,
,
故答案为:.
(3),
,
即,
,
,
故答案为:.
本题考查无理数的估算和不等式的计算.
(1)利用根据的估算可得:,再根据 的定义可得:;
(2)利用根据的估算可得:,再根据 的定义可得:;
(3)因为,根据 的定义可得:,进而可求出,再进行计算可求出x的取值范围.
14.
15.;
16.(1)解;原式
;
(2)解:原式
(1)先化简括号内的二次根式并合并,最后计算二次根式的除法求解即可;
(2)先根据同底数幂乘法和积的乘方的逆运算把原式化为,再去绝对值和计算零指数次幂,然后合并解题即可.
17.(1)解:边长分别为3,4,5的三角形如下图1
(2)解:面积为5的正方形如下图2
(3)解:分别为2、、的三角形如下图3.
(1)画出一个直角边长分别为3和4的直角三角形即可;
(2)画出一个边长为的正方形即可;
(3)根据勾股定理画出三边长分别为2、、的三角形即可.
18.(1)7;6;6.5
(2)解:应派甲选手参赛.
理由:甲队员与乙队员的平均成绩一样,而甲队员的众数、中位数均比乙大,且甲队员的方差小,发挥比较稳定,所以选择甲队员参加比赛.
解:(1)甲队员的平均成绩为:a=(5×1+6×2+7×4+8×2+9×1)÷10=7;
将乙队员的10次射击成绩按从小到大的顺序排列为:3、5、6、6、6、7、8、9、10、10,
∴乙队员10次射击成绩的中位数为:C=(6+7)÷2=6.5;
10次射击成绩中出现次数最多的是6,共出现了3次,∴乙队员射击成绩的众数b=6;
故答案为:7,6,6.5;
(1)利用平均数的计算公式直接计算出甲队员的平均分即可;众数:在一组数据中,出现次数最多的数据叫做众数,(众数可能有多个);中位数:将一组数据按从小到大(或者从大到小)的顺序排列后,如果数据的个数是奇数个时,则处在最中间的那个数据叫做这组数据的中位数;如果数据的个数是偶数个时,则处在最中间的两个数据的平均数 叫做这组数据的中位数,据此可得出b、c的值;
(2)甲队员与乙队员的平均成绩一样,而甲队员的众数、中位数均比乙大,且甲队员的方差小,发挥比较稳定,所以选择甲队员参加比赛.
19.(1)甲种模型的单价为20元,乙种模型的单价30元
(2)一共有3种方案:购买甲种模型28套,购买乙种模型22套;购买甲种模型29套,购买乙种模型21套;购买甲种模型30套,购买乙种模型20套.
20.(1)3
(2)画出该函数图象的另一部分如图;
(3);增大
(4)或
(1)解:当x=-1时,,
∴m=3,
故答案为:3;
(3)①观察图象可得,该函数图象的最低点坐标是(2,0);
②当时,y随x的增大而减小;当时,y随x的增大而增大;
故答案为:①(2,0),②增大;
(4)由题意,得,函数与函数的图象只有一个交点,
观察图象可得:此时的取值范围是或;
故答案为:或.
(1)把x=-1代入函数的解析式,求出对应的函数值,可以求得m的值;
(2)利用表格的数据确定点的坐标,再描点连线画出相应的函数图象;
(3)观察函数图象,利用图象的性质即可得出结论;
(4)把方程只有一个解,转化为函数只有一个交点,观察函数图象,可以得到满足题意的K的取值范围;
21.(1)40;60
(2)天;
(3)米,
设乙队的函数解析式为,
把,和,代入,
得,
解之得,
;
(4)当时,
米,
米.
解:(1)根据题意,80020=40米/天;
3606=60米/天
故填:40、60
(1)根据图中数据,可以求得甲乙的修筑速度;
(2)读图可知乙队在修筑6天后离开,在甲队修筑360米后回来,故先求甲修筑360米需用的天数,减去6天即可知道离开天数;
(3)设出所求函数的一般式y=kx+b,有2个未知数,找到图象经过的两点坐标,代入求得解析式并标明x的取值范围;
(4)公路的总长度是甲乙两队修筑之和。
20224-2025学年八年级上册期末押题卷(人教版)
数学
考试范围:七上全册 考试时间:100分钟
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
一、单选题
1.如图,在一次活动中,位于处的班准备前往相距的处与班会合,那么用方向和距离描述班相对于班的位置是( )
A.南偏西,距离 B.北偏东,距离
C.南偏西,距离 D.北偏东,距离
2.在实数(不循环)、、、、、、、、中,无理数的个数为( )
A.2个 B.3个 C.4个 D.5个
3.如图,,CE平分,若,则的度数是( )
A.25° B.50° C.65° D.130°
4.如图,在平面直角坐标系中,点,,,和,,,分别在直线和轴上,,,,都是等腰直角三角形(点,,,为直角顶点),那么点的坐标是( )
A. B. C. D.
5.一次函数的图象不经过( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
6.某公司招聘员工,将笔试和面试两项测试得分按的比例确定个人的测试成绩.若张红笔试成绩为95分,面试成绩为90分,则她的测试成绩是( )
A.分 B.分 C.分 D.分
7.小丽同学带11元钱去买钢笔和笔记本(两种文具都买),钢笔每支3元,笔记本每本1元,那么钢笔能买( )
A.1支 B.1支或2支或3支
C.2支 D.2支或3支
8.已知直线y=﹣3x+m过点A(﹣1,y1)和点(﹣3,y2),则y1和y2的大小关系是( )
A.y1>y2 B.y1<y2 C.y1=y2 D.不能确定
9.我国古代数学著作《孙子算经》有“多人共车”问题:“今有三人共车,二车空;二人共车,九人步.问:人与车各几何 ”其大意如下:有若干人要坐车,如果每3人坐一辆车,那么有2辆空车;如果每2人坐一辆车,那么有9人需要步行,问人与车各多少 设共有 人, 辆车,则可列方程组为( )
A. B.
C. D.
10.如图,把正方形铁片置于平面直角坐标系中,顶点的坐标为,点在正方形铁片上,将正方形铁片绕其右下角的顶点按顺时针方向依次旋转,第一次旋转至图①位置,第二次旋转至图②位置,…则正方形铁片连续旋转次后,点的坐标为( )
A. B. C. D.
二、填空题
11.“等腰三角形两底角相等”的逆命题是 ,这个逆命题是 命题.
12. 已知关于 的方程组 的解及 都是正整数. 则: (1) 当 时,方程组的解是 ,(2) 满足条件的所有解的个数是
13.规定:用符号表示一个不大于实数的最大整数,例如:,,,按这个规定:
(1) ;(2) ;
(3)若,则的取值范围是 .
14.如图,圆柱体中底面周长是,是底面直径,高,点是上一点且,一只从点出发沿着圆柱体的侧面爬行到点,则小虫爬行的最短路程是 .
15.在平面直角坐标系中,已知,点在以为圆心,为半径的圆上运动,作点关于直线、的对称点、,则 ,DE的最小值为 .
三、解答题
16.计算
(1)
17.如图,正方形网格中的每个小正方形的边长都是1,每个小格的顶点叫做格点.
(1)在图1中以格点为顶点画一个三角形,使三角形三边长分别为3,4,5;
(2)在图2中以格点为顶点画一个面积为5的正方形;
(3)在图3中以格点为顶点画一个三角形,使三角形三边长分别为2、、.
18.甲,乙两名队员参加训练,每人射击10次的成绩分别被制成下列两个统计图:
根据以上信息,整理分析数据如下:
平均成绩环 众数/环 中位数/环 方差/环2
甲 a 7 7 1.2
乙 7 b c 4.6
(1)写出表格中a,b,c的值: , , ;
(2)根据以上统计数据,你会选择谁参加比赛,请说明理由.
19.为迎接培圣校园科技节的到来,学校科技社团欲购买甲、乙两种模型进行组装,已知3套甲模型的总价与2套乙模型的总价相等,若购买1套甲模型和2套乙模型共需80元.
(1)求甲、乙两种模型的单价各是多少元?
(2)现计划用1220元资金,在不超过预算的情况下,购买这两种模型共50套,且乙种模型的数量不少于甲种模型数量的,求两种模型共有多少种选购方案.
20.某班“数学兴趣小组”根据学习一次函数的经验,对函数的图象和性质进行了研究探究过程如下,请补充完整.
(1)自变量的取值范围是全体实数下表是与的几组对应值:
其中, ;
(2)如下图,在平面直角坐标系中,描出了以上表中各对对应值为坐标的点,并画出了函数图象的一部分,请画出该函数图象的另一部分;
(3)观察函数图象发现,该函数图象的最低点坐标是 ;
当时,随的增大而减小;当时,随的增大而 ;
(4)进一步探究,若关于的方程只有一个解,则的取值范围是 .
21.甲、乙两个工程队修筑一条公路,甲队从南向北方向修筑,乙队从北向南方向修筑甲、乙两队同时开工,乙队施工几天后因另有任务提前离开,甲队继续修筑公路当乙队任务完成后,因赶时间,乙队回来继续修筑公路,直到公路修通在修路过程中,甲、乙两队的工作效率保持不变设甲、乙两队修筑公路的长度为米,施工时间为天,与之间的函数图象如图所示.
(1)甲队每天修筑公路 米,乙队每天修筑公路 米;
(2)求乙队离开的天数;
(3) 求乙队回来后修筑公路的长度与之间的函数关系式,并写出自变量的取值范围;
(4) 求这条公路的总长度.
答案解析部分
1.D
2.C
3.D
解:,,
,,
平分,
,
.
故答案为:D.
根据平行线的性质得,,根据角平分线的定义得,代数求解即可.
4.D
5.A
6.C
7.B
解:设能买x支钢笔和y个笔记本,根据题意得:
3x+y=11,
∵x、y为正整数,
当x=1时,y=8;
当x=2时,y=5;
当x=3时,y=2;
当x=4时,y=-1(舍去).
∴钢笔能买1支或2支或3支.
故答案为:B
设能买x支钢笔和y个笔记本,根据:钢笔的费用+笔记本的费用=11元列出方程,然后求出其正整数解即可.
8.B
解:∵函数y=-3x+m中,k=-3<0,
∴y随x的增大而减小,
∵函数y=-3x+m的图象经过点A(-l,y1)和点B(-3,y2),
-3<-1,
∴y1<y2,
故答案为:B.
根据一次函数的解析式可以知道:y随x的增大而减小,利用此性质求解即可。
9.C
解:设共有 人, 辆车,则
故答案为:C
设共有 人, 辆车,根据“ 如果每3人坐一辆车,那么有2辆空车;如果每2人坐一辆车,那么有9人需要步行 ”列出方程组即可.
10.C
11.有两个角相等的三角形是等腰三角形;真
12.;6
解:(1)、解方程组 ,得,则明显可知a为6的倍数.
又∵a≤6,
∴a=6.
∴故方程的解为:;
(2)、由题干条件可知,a的取值有6、12、18、24、30、36,对应的解的个数为6个.
故答案为:6
(1)先解方程组,再根据已知求出满足条件的所有正整数a,然后将a的值代入求解即可;
(2)根据(1)x、y的表达式,结合条件求出满足条件的所有正整数a,a有多少个可能的取值,则对应多少个解.
13.1;;
(1),
,
故答案为:1.
(2),
,
,
故答案为:.
(3),
,
即,
,
,
故答案为:.
本题考查无理数的估算和不等式的计算.
(1)利用根据的估算可得:,再根据 的定义可得:;
(2)利用根据的估算可得:,再根据 的定义可得:;
(3)因为,根据 的定义可得:,进而可求出,再进行计算可求出x的取值范围.
14.
15.;
16.(1)解;原式
;
(2)解:原式
(1)先化简括号内的二次根式并合并,最后计算二次根式的除法求解即可;
(2)先根据同底数幂乘法和积的乘方的逆运算把原式化为,再去绝对值和计算零指数次幂,然后合并解题即可.
17.(1)解:边长分别为3,4,5的三角形如下图1
(2)解:面积为5的正方形如下图2
(3)解:分别为2、、的三角形如下图3.
(1)画出一个直角边长分别为3和4的直角三角形即可;
(2)画出一个边长为的正方形即可;
(3)根据勾股定理画出三边长分别为2、、的三角形即可.
18.(1)7;6;6.5
(2)解:应派甲选手参赛.
理由:甲队员与乙队员的平均成绩一样,而甲队员的众数、中位数均比乙大,且甲队员的方差小,发挥比较稳定,所以选择甲队员参加比赛.
解:(1)甲队员的平均成绩为:a=(5×1+6×2+7×4+8×2+9×1)÷10=7;
将乙队员的10次射击成绩按从小到大的顺序排列为:3、5、6、6、6、7、8、9、10、10,
∴乙队员10次射击成绩的中位数为:C=(6+7)÷2=6.5;
10次射击成绩中出现次数最多的是6,共出现了3次,∴乙队员射击成绩的众数b=6;
故答案为:7,6,6.5;
(1)利用平均数的计算公式直接计算出甲队员的平均分即可;众数:在一组数据中,出现次数最多的数据叫做众数,(众数可能有多个);中位数:将一组数据按从小到大(或者从大到小)的顺序排列后,如果数据的个数是奇数个时,则处在最中间的那个数据叫做这组数据的中位数;如果数据的个数是偶数个时,则处在最中间的两个数据的平均数 叫做这组数据的中位数,据此可得出b、c的值;
(2)甲队员与乙队员的平均成绩一样,而甲队员的众数、中位数均比乙大,且甲队员的方差小,发挥比较稳定,所以选择甲队员参加比赛.
19.(1)甲种模型的单价为20元,乙种模型的单价30元
(2)一共有3种方案:购买甲种模型28套,购买乙种模型22套;购买甲种模型29套,购买乙种模型21套;购买甲种模型30套,购买乙种模型20套.
20.(1)3
(2)画出该函数图象的另一部分如图;
(3);增大
(4)或
(1)解:当x=-1时,,
∴m=3,
故答案为:3;
(3)①观察图象可得,该函数图象的最低点坐标是(2,0);
②当时,y随x的增大而减小;当时,y随x的增大而增大;
故答案为:①(2,0),②增大;
(4)由题意,得,函数与函数的图象只有一个交点,
观察图象可得:此时的取值范围是或;
故答案为:或.
(1)把x=-1代入函数的解析式,求出对应的函数值,可以求得m的值;
(2)利用表格的数据确定点的坐标,再描点连线画出相应的函数图象;
(3)观察函数图象,利用图象的性质即可得出结论;
(4)把方程只有一个解,转化为函数只有一个交点,观察函数图象,可以得到满足题意的K的取值范围;
21.(1)40;60
(2)天;
(3)米,
设乙队的函数解析式为,
把,和,代入,
得,
解之得,
;
(4)当时,
米,
米.
解:(1)根据题意,80020=40米/天;
3606=60米/天
故填:40、60
(1)根据图中数据,可以求得甲乙的修筑速度;
(2)读图可知乙队在修筑6天后离开,在甲队修筑360米后回来,故先求甲修筑360米需用的天数,减去6天即可知道离开天数;
(3)设出所求函数的一般式y=kx+b,有2个未知数,找到图象经过的两点坐标,代入求得解析式并标明x的取值范围;
(4)公路的总长度是甲乙两队修筑之和。
同课章节目录
