2024-2025学年苏科版八年级数学上册期末押题卷(含答案+解析)
文档属性
| 名称 | 2024-2025学年苏科版八年级数学上册期末押题卷(含答案+解析) |  | |
| 格式 | docx | ||
| 文件大小 | 596.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-09 21:32:44 | ||
图片预览




文档简介
保密★启用前
20224-2025学年八年级上册期末押题卷(苏科教版)
数学
考试范围:八上全册 考试时间:100分钟 分值:120分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
一、选择题(每题3分,共24分)
1.下列说法中,正确的是( )
A.,,都是无理数
B.绝对值最小的实数是0
C.实数分为正实数和负实数两类
D.无理数包括正无理数、负无理数和零
2.如图,在平面直角坐标系中,第一象限内的点P在射线OA上,OP=13,cosα=,则点P的坐标为( )
A.(5,13) B.(5,12) C.(13,5) D.(12,5)
3.下列运算正确的是( )
A. =±6 B.4 ﹣3 =1
C. =6 D. =6
4.如图,中,、的角平分线、交于点P,延长、,,,则下列结论中正确的个数( )
①平分; ②;
③; ④.
A.1个 B.2个 C.3个 D.4个
5.下列函数图象中不可能是一次函数 的图象的是( )
A. B.
C. D.
6.一次函数的图象经过第一、二、四象限,若点在该一次函数的图象上,则的大小关系是( )
A. B. C. D.无法判定
7.如图,在平行四边形中ABCD,AD=7,CE平分∠BCD,交边于点E,且AE=3,则AB的长为( )
A.2 B. C.3 D.4
8.数形结合是解决数学问题常用的思想方法. 如图,一次函数 为常数, 且 的图象与直线 都经过点 ,当 时, 根据图象可知, 的取值范围是( )
A. B. C. D.
二、填空题(每题3分,共30分)
9.16的算术平方根是
10.现定义一个新运算“※”,规定对于任意实数x,y,都有,则的值为 .
11.用四舍五入法把3.1415926精确到0.01,所得到的近似数为 .
12. 已知的整数部分为,的小数部分为,则的值 .
13.如图, 正方形的边长是,菱形的边长是,则菱形的对角线的长是 .
14.如图,在中,,,为边上的一动点,以为邻边作,则对角线长度的最小值 .
15.如图,在中,,以的三边为边向外作正方形,正方形,正方形,连接,,作交于点P,记正方形和正方形的面积分别为,,若,,则:等于 .
16.如图,在平面直角坐标系中,一次函数的图象分别交、轴于点、,将直线绕点按顺时针方向旋转,交轴于点,则直线的函数表达式是 .
17.已知和都是等腰三角形,且,顶角,等腰 的顶点D在边上滑动,点E在边的延长线上滑动.将线段绕点D逆时针旋转得到线段,连接,若是以为腰的等腰三角形,则 .
18.一次函数(为常数,且)中的与的部分对应值如下表:
2
0
下列结论中:①方程的解为;②若,则;③若的解为,则;④若关于的不等式的解集为,则.一定正确的是 .
三、解答题(共8题,共66分)
19.(1)计算:
解方程:
20.已知,如图,,平分交于D,求的度数.
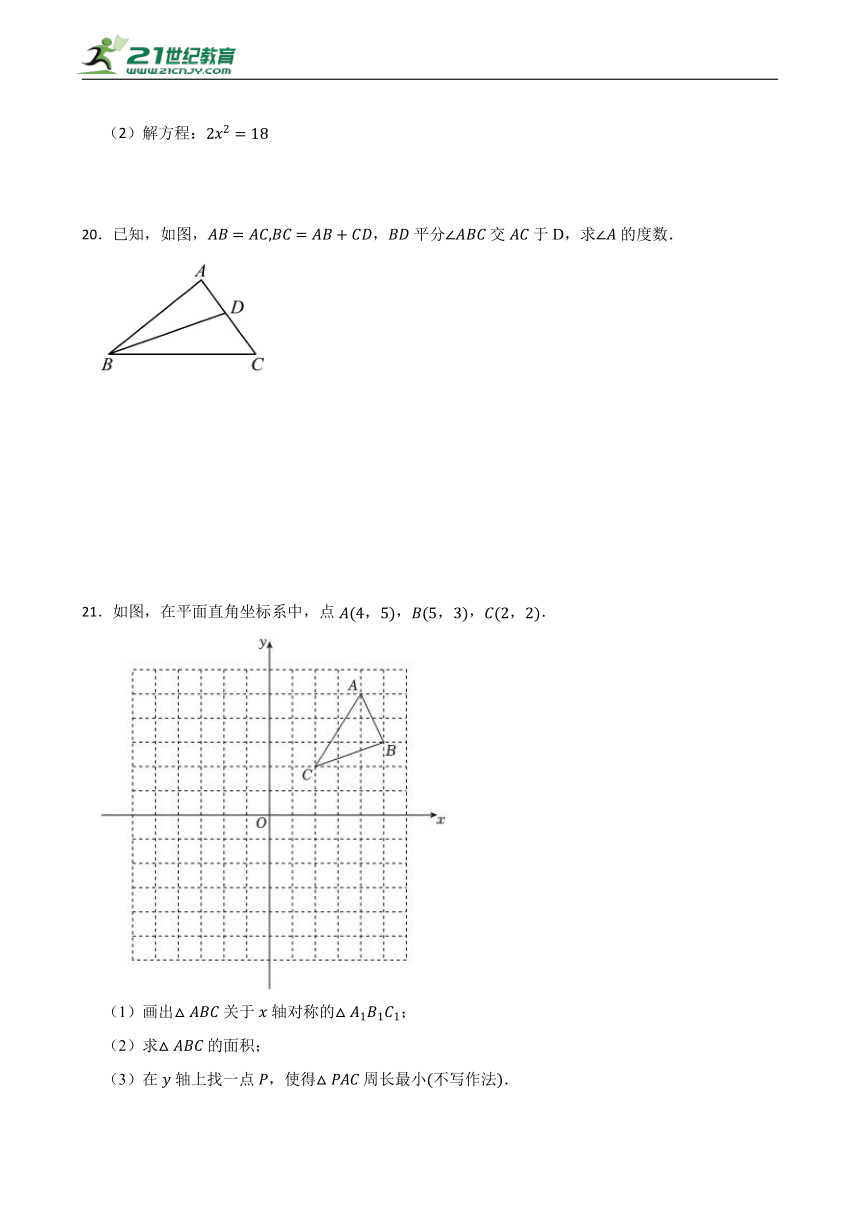
21.如图,在平面直角坐标系中,点,,.
(1)画出关于轴对称的;
(2)求的面积;
(3)在轴上找一点,使得周长最小不写作法.
22.如图,一张三角形纸片,已知,,,,将该纸片折叠,若折叠后点与点重合,折痕与边交于点,与边交于点.
(1)求的面积.
(2)求折痕的长.
23.利用网格线画图:如图,点、、都在正方形网格的格点上.
(1)在上找一点,使;
(2)在上找一点,使点到和的距离相等.
24.如图,在平面直角坐标系中,一次函数的图象经过点入A(-2,6)与x轴交于点B,与正比例函数的图象交于点C,且点C的横坐标为1.
(1)求k,b的值;
(2)由图象可知,当x 时,;
(3)若点D在y轴的负半轴上,且满足,求点D的坐标.
六六乘船由源头甲地顺流而下到乙地,马上又逆流而上到距甲地2千米的丙地,已知他共乘船3小时,船在静水中的速度是每小时8千米,水流速度是每小时2千米,则甲乙两地相距千米.
26.问题:探究函数的图象与性质.
数学兴趣小组根据学习一次函数的经验,对函数的图象与性质进行了探究:
(1)在函数,自变量x可以是任意实数,下表是y与x的几组对应值:
x … 0 1 2 3 4 …
y 3 2 1 0 0 a
①表格中a的值为 ;
②若为该函数图象上的点,则 ;
(2)在平面直角坐标系中,描出上表中的各点,画出该函数的图象;
(3)结合图象回答下列问题:
①当 时,函数有最小值为 ;
②当自变量x满足什么条件时,函数值?
答案解析部分
1.B
解:A、 ,是无理数,是有理数,A不符合题意;
B、绝对值最小的实数是0,B符合题意;
C、实数分为正实数、负实数和0,C不符合题意;
D、无理数包括正无理数、负无理数,D不符合题意.
故答案为:B.
根据无理数的定义、实数的分类和无理数的分类即可解答.
2.B
3.D
解: 故A不符合题意,
故B不符合题意,
故C不符合题意,
故D符合题意,
故答案为:D.
根据算术平方根、二次根式的加减、二次根式的乘除分别求解,然后判断即可.
4.D
解:①如图,过点作于点,
∵、的角平分线、交于点,,,
∴,,,
∴,
在和中,
,
∴,
∴,,
∴平分,①正确;
②在和中,
,
∴,
∴,
∴,
∵,,
∴,
∴,
∴,②正确;
③∵,,,
∴,
又∵,
∴,
∴,③正确;
④∵,,
∴,,
∴,即,④正确;
综上,结论中正确的个数4个,
故选:D.
本题考查角平分线的性质定理、直角三角形全等的判定与性质、四边形的内角和.过点作于点,先利用角平分线的性质定理可得,利用等量代换可得,利用直角三角形全等的判定定理可证明:,根据全等三角形的性质可得,据此可判断说法①;利用直角三角形全等的判定定理可证明:,根据全等三角形的性质可得,利用角的运算可得:,根据垂直的定义可得:,进而可得:,再进行等量替换可判断说法②;先根据三角形的外角性质可得,再利用角的运算可得,再根据三角形的外角性质可得:,再结合:,通过运算可判断说法③;根据全等三角形的性质可得,,据此可得: ,通过观察图形可得: ,据此可判断说法④.
5.B
解:根据图象知:
A、a>0,-(a-2)>0,解得0B、a<0,-(a-2)<0,解得两不等式没有公共部分,所以不可能;
C、a<0,-(a-2)>0,解得a<0,所以有可能;
D、a>0,-(a-2)<0,解得a>2,所以有可能.
故答案为:B.
根据图象,确定一次项系数及常数项的性质符号,再作判断,若不等式的解集有公共部分,则有可能;反之,则不可能.
6.A
7.D
8.A
解:由图象可得,
当x>3时,直线在一次函数y=kx+b的上方,
∴当时,x的取值范围是x>3,
故答案为:A.
根据题意和函数图象,可以写出当时,x的取值范围.
9.4
∵4 =16,
∴=4.
根据算术平方根的定义即可求出结果.
10.8
解: .
故答案为:8
利用定义运算法则: ,先列式,再利用算术平方根和立方根的性质,可求出结果.
11.3.14
解:,
故答案为:3.14.
根据近似数和有效数字的定义及四舍五入的方法求解即可。
12.
解:∵
∴
∴的整数部分为7,
∴
同理的小数部分为:
∴
∴
故答案为:.
利用无理数大小的估算即可求出m和n的值,最后将其代入计算即可求解.
13.
14.
15.
如图所示,过点P作PM⊥CB,交CB的延长线于点M,作PN⊥CA,交CA的延长线于点N,
由题可得,∠BCG=45°,CP⊥ CG,
∴∠BCP=45°,
又∵∠ACB=90°,
∴∠ACP=45°,即CP平分∠ ACB,
又∵PM⊥BC,PN⊥AC,
∴ PM=PN,
∵正方形ACDE和正方形AHIB的面积分别为S1,S2,且S1=4,S2=7,
∴正方形BCFG的面积=7-4=3,
∴正方形ACDE和正方形BCFG的面积之比为4:3,
∴,
∴,
故答案为:.
本题首先作出辅助线,得到PM=PN,再根据两个正方形的面积之比得到AC与BC的比,通过AC与BC的比即可得到两个三角形的面积之比.
16.
解:过点A作AD⊥BC于点D,过点D作DE⊥x轴于点E,如图,
∵ ∠ABD=45°,AD⊥AB,
∴ △ABD是等腰直角三角形,
∴ AB=AD,
∵ ∠BAD=90°,
∴ ∠OAB+∠EAD=90°,
∵ ∠OAB+∠OBA=90°,
∴ ∠EAD=∠OBA,
∵ ∠AOB=∠DEA=90°,
∴ △AOB≌△DEA(AAS),
∴ DE=AO,AE=BO,
∵ y=2x-2,
∴ A(1,0),B(0,-2),
∴ OA=1,OB=2,
∴ D(3,-1),
设BC的函数表达式为y=kx+b,
∴,
∴ k=,b=-2,
∴ y=x-2.
故答案为: y=x-2.
过点A作AD⊥BC于点D,过点D作DE⊥x轴于点E,根据等腰直角三角形的判定和性质可得AB=AD,证明出∠EAD=∠OBA,根据AAS判定△AOB≌△DEA推出 DE=AO,AE=BO,从而得到D点坐标,根据待定系数法,即可求得.
17.或
解:∵和都是等腰三角形,且,顶角,
∴FD=ED,∠CAB=72°,∠FDE=36°,∠EAD=108°,
由旋转得GD=AD,∠GDA=36°,
∴∠FDG=∠EDA,
易证△FDG≌△EDA(SAS),
∴∠FGD=∠EAD=108°,GF=EA,
当GF=EG时,如图所示:
易证△FGD≌△EGD(SSS),
∴∠EGD=108°,
∴∠FGE=144°;
当GF=EF时,如图所示:
∵GD=AD,∠GDA=36°,
∴∠AGD=∠GAD=72°,
∴∠FGD+∠AGD=180°,∠EAG=36°,
∴A、F、G共线,
∵GF=EF,GF=EA,
∴EF=EA,
∴∠EFG=∠EAG=36°,
∴∠FGE=72°,
综上所述,或,
故答案为:或
先根据三角形全等的性质结合等腰三角形的性质即可得到FD=ED,∠CAB=72°,∠FDE=36°,∠EAD=108°,进而根据旋转的性质得到GD=AD,∠GDA=36°,从而得到∠FDG=∠EDA,再根据三角形全等的判定与性质证明△FDG≌△EDA(SAS)即可得到∠FGD=∠EAD=108°,GF=EA,分类讨论:当GF=EG时,易证△FGD≌△EGD(SSS),进而结合题意即可求解;当GF=EF时,根据等腰三角形的性质结合题意得到∠AGD=∠GAD=72°,∠FGD+∠AGD=180°,∠EAG=36°,进而得到A、F、G共线,再根据等腰三角形的性质结合题意即可求解。
18.①②④
解:① 一次函数 ,由表格数据知:当y=0时x=2,
∴ 方程的解为 ,故①正确;
② 若,则一次函数经过一、二、四象限,
∴m<0,n>0,
∴,故②正确;
③由y=0.5x-1中,当y=0时,x=2,
∴直线y=0.5x-1与都经过(2,0),
由图象可知:当x>2时,直线y=0.5x-1的图象在直线图象的上方,
∴m>-1,故③错误;
④∵ 关于的不等式的解集为 ,
∴直线与y=x的交点为(,),
把(2,0)(,)代入中,得,
解得:m=-2,故④正确;
故答案为:①②④.
由表格知数据直接判断①;由可知一次函数经过一、二、四象限,据此确定m、n的符号,据此判断②;当x>2时,直线y=0.5x-1的图象在直线图象的上方,可确定m>-1,据此判断③;由关于的不等式的解集为 ,可确定直线与y=x的交点为(,),利用待定系数法求出m值,即可判断④.
19.(1)解:
=
=
=;
(2)解:
.
(1)运用有理数的乘方、二次根式的混合运算、立方根进行运算,再合并同类项即可求解;
(2)运用直接开平方法解一元二次方程即可求解。
20.
21.(1)解:见解析,即为所求;
(2)解:的面积
;
(3)解:见解析,点即为所求.
解:(1)如图,即为所求作的三角形;
(2);
(3)先作出点A关于y轴的对称点,连接交y轴于一点,该点即为所求作的点P,如图所示:
∵点A关于y轴的对称点,
∴,
∴,
∵两点之间线段最短,
∴此时的周长最小.
(1)先根据轴对称的性质作出点A、B、C关于x轴的对称点、、,然后顺次连接即可;
(2)利用坐标与距离的关系,结合三角形的面积公式,采用割补法求出的面积即可;
(3)先作出点A关于y轴的对称点,连接交y轴于一点,即为点P.
22.(1)解:∵,,,
∴,
∴为直角三角形,,
∴的面积.
(2)解:如下图,连接,
由折叠可知,,
即,
∴垂直平分,
∴,
设,则,
在中,有,
即,解得,
∴,
∴在中,可有,
即折痕的长为.
(1)先利用勾股定理的逆定理证出为直角三角形,,再利用三角形的面积公式求解即可;
(2)连接BD,设,则,利用勾股定理可得,即,解得,再求出BD的长,最后利用勾股定理求出DE的长即可.
23.(1)答案见试题解析;(2)答案见试题解析.
24.(1)解:∵点C的横坐标为1
∴当x=1时,
∴C(1,3)
∵A(-2,6)
∴有
解得:
(2)<1
(3)解:设D(0,m)
由(1)知:
取,则,解得∴B(4,0)
∵
∴
解得:∴
∵∴
∴点D的坐标为(0,-4)
解:(2)由(1)可知y1=-x+4,
解之:,
∴点C(1,3),
由图象可知当x<1时y1>y2.
故答案为:<1
(1)由点C的横坐标可求出点C的坐标,利用点A,C的坐标可求出k,b的值.
(2)将两函数解析式联立方程组,可求出点C的坐标,利用点C的横坐标可求出y1>y2时x的取值范围.
(3)设D(0,m)(m<0),利用函数解析式求出点B的坐标,根据 可得到关于m的方程,解方程求出m的值,可得到点D的坐标.
25.10或12.5千米
26.(1)1;或11
(2)解:该函数图象如图:
(3)解:①;或;根据(2)图象可直接看出,当或时,.
解:
(1) ① 当x=4时,y=a=,∴ a=1
②若为该函数图象上的点, 当x=b时,y=8.代入得:,解得b=-9或b=11
∴ b=-9或11
(2)画函数图象的步骤:列表,描点,连线。
(3) ① 由(2)图象可知,当x=1时,函数最小值为-2
② 当y≥0时,x≤-1或x≥3
本题考查函数图象和性质。根据表格中自变量x的值和因变量y的值,可画出函数图象,可得函数的最小值,找出函数和一次不等式的关系。
20224-2025学年八年级上册期末押题卷(苏科教版)
数学
考试范围:八上全册 考试时间:100分钟 分值:120分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
一、选择题(每题3分,共24分)
1.下列说法中,正确的是( )
A.,,都是无理数
B.绝对值最小的实数是0
C.实数分为正实数和负实数两类
D.无理数包括正无理数、负无理数和零
2.如图,在平面直角坐标系中,第一象限内的点P在射线OA上,OP=13,cosα=,则点P的坐标为( )
A.(5,13) B.(5,12) C.(13,5) D.(12,5)
3.下列运算正确的是( )
A. =±6 B.4 ﹣3 =1
C. =6 D. =6
4.如图,中,、的角平分线、交于点P,延长、,,,则下列结论中正确的个数( )
①平分; ②;
③; ④.
A.1个 B.2个 C.3个 D.4个
5.下列函数图象中不可能是一次函数 的图象的是( )
A. B.
C. D.
6.一次函数的图象经过第一、二、四象限,若点在该一次函数的图象上,则的大小关系是( )
A. B. C. D.无法判定
7.如图,在平行四边形中ABCD,AD=7,CE平分∠BCD,交边于点E,且AE=3,则AB的长为( )
A.2 B. C.3 D.4
8.数形结合是解决数学问题常用的思想方法. 如图,一次函数 为常数, 且 的图象与直线 都经过点 ,当 时, 根据图象可知, 的取值范围是( )
A. B. C. D.
二、填空题(每题3分,共30分)
9.16的算术平方根是
10.现定义一个新运算“※”,规定对于任意实数x,y,都有,则的值为 .
11.用四舍五入法把3.1415926精确到0.01,所得到的近似数为 .
12. 已知的整数部分为,的小数部分为,则的值 .
13.如图, 正方形的边长是,菱形的边长是,则菱形的对角线的长是 .
14.如图,在中,,,为边上的一动点,以为邻边作,则对角线长度的最小值 .
15.如图,在中,,以的三边为边向外作正方形,正方形,正方形,连接,,作交于点P,记正方形和正方形的面积分别为,,若,,则:等于 .
16.如图,在平面直角坐标系中,一次函数的图象分别交、轴于点、,将直线绕点按顺时针方向旋转,交轴于点,则直线的函数表达式是 .
17.已知和都是等腰三角形,且,顶角,等腰 的顶点D在边上滑动,点E在边的延长线上滑动.将线段绕点D逆时针旋转得到线段,连接,若是以为腰的等腰三角形,则 .
18.一次函数(为常数,且)中的与的部分对应值如下表:
2
0
下列结论中:①方程的解为;②若,则;③若的解为,则;④若关于的不等式的解集为,则.一定正确的是 .
三、解答题(共8题,共66分)
19.(1)计算:
解方程:
20.已知,如图,,平分交于D,求的度数.
21.如图,在平面直角坐标系中,点,,.
(1)画出关于轴对称的;
(2)求的面积;
(3)在轴上找一点,使得周长最小不写作法.
22.如图,一张三角形纸片,已知,,,,将该纸片折叠,若折叠后点与点重合,折痕与边交于点,与边交于点.
(1)求的面积.
(2)求折痕的长.
23.利用网格线画图:如图,点、、都在正方形网格的格点上.
(1)在上找一点,使;
(2)在上找一点,使点到和的距离相等.
24.如图,在平面直角坐标系中,一次函数的图象经过点入A(-2,6)与x轴交于点B,与正比例函数的图象交于点C,且点C的横坐标为1.
(1)求k,b的值;
(2)由图象可知,当x 时,;
(3)若点D在y轴的负半轴上,且满足,求点D的坐标.
六六乘船由源头甲地顺流而下到乙地,马上又逆流而上到距甲地2千米的丙地,已知他共乘船3小时,船在静水中的速度是每小时8千米,水流速度是每小时2千米,则甲乙两地相距千米.
26.问题:探究函数的图象与性质.
数学兴趣小组根据学习一次函数的经验,对函数的图象与性质进行了探究:
(1)在函数,自变量x可以是任意实数,下表是y与x的几组对应值:
x … 0 1 2 3 4 …
y 3 2 1 0 0 a
①表格中a的值为 ;
②若为该函数图象上的点,则 ;
(2)在平面直角坐标系中,描出上表中的各点,画出该函数的图象;
(3)结合图象回答下列问题:
①当 时,函数有最小值为 ;
②当自变量x满足什么条件时,函数值?
答案解析部分
1.B
解:A、 ,是无理数,是有理数,A不符合题意;
B、绝对值最小的实数是0,B符合题意;
C、实数分为正实数、负实数和0,C不符合题意;
D、无理数包括正无理数、负无理数,D不符合题意.
故答案为:B.
根据无理数的定义、实数的分类和无理数的分类即可解答.
2.B
3.D
解: 故A不符合题意,
故B不符合题意,
故C不符合题意,
故D符合题意,
故答案为:D.
根据算术平方根、二次根式的加减、二次根式的乘除分别求解,然后判断即可.
4.D
解:①如图,过点作于点,
∵、的角平分线、交于点,,,
∴,,,
∴,
在和中,
,
∴,
∴,,
∴平分,①正确;
②在和中,
,
∴,
∴,
∴,
∵,,
∴,
∴,
∴,②正确;
③∵,,,
∴,
又∵,
∴,
∴,③正确;
④∵,,
∴,,
∴,即,④正确;
综上,结论中正确的个数4个,
故选:D.
本题考查角平分线的性质定理、直角三角形全等的判定与性质、四边形的内角和.过点作于点,先利用角平分线的性质定理可得,利用等量代换可得,利用直角三角形全等的判定定理可证明:,根据全等三角形的性质可得,据此可判断说法①;利用直角三角形全等的判定定理可证明:,根据全等三角形的性质可得,利用角的运算可得:,根据垂直的定义可得:,进而可得:,再进行等量替换可判断说法②;先根据三角形的外角性质可得,再利用角的运算可得,再根据三角形的外角性质可得:,再结合:,通过运算可判断说法③;根据全等三角形的性质可得,,据此可得: ,通过观察图形可得: ,据此可判断说法④.
5.B
解:根据图象知:
A、a>0,-(a-2)>0,解得0
C、a<0,-(a-2)>0,解得a<0,所以有可能;
D、a>0,-(a-2)<0,解得a>2,所以有可能.
故答案为:B.
根据图象,确定一次项系数及常数项的性质符号,再作判断,若不等式的解集有公共部分,则有可能;反之,则不可能.
6.A
7.D
8.A
解:由图象可得,
当x>3时,直线在一次函数y=kx+b的上方,
∴当时,x的取值范围是x>3,
故答案为:A.
根据题意和函数图象,可以写出当时,x的取值范围.
9.4
∵4 =16,
∴=4.
根据算术平方根的定义即可求出结果.
10.8
解: .
故答案为:8
利用定义运算法则: ,先列式,再利用算术平方根和立方根的性质,可求出结果.
11.3.14
解:,
故答案为:3.14.
根据近似数和有效数字的定义及四舍五入的方法求解即可。
12.
解:∵
∴
∴的整数部分为7,
∴
同理的小数部分为:
∴
∴
故答案为:.
利用无理数大小的估算即可求出m和n的值,最后将其代入计算即可求解.
13.
14.
15.
如图所示,过点P作PM⊥CB,交CB的延长线于点M,作PN⊥CA,交CA的延长线于点N,
由题可得,∠BCG=45°,CP⊥ CG,
∴∠BCP=45°,
又∵∠ACB=90°,
∴∠ACP=45°,即CP平分∠ ACB,
又∵PM⊥BC,PN⊥AC,
∴ PM=PN,
∵正方形ACDE和正方形AHIB的面积分别为S1,S2,且S1=4,S2=7,
∴正方形BCFG的面积=7-4=3,
∴正方形ACDE和正方形BCFG的面积之比为4:3,
∴,
∴,
故答案为:.
本题首先作出辅助线,得到PM=PN,再根据两个正方形的面积之比得到AC与BC的比,通过AC与BC的比即可得到两个三角形的面积之比.
16.
解:过点A作AD⊥BC于点D,过点D作DE⊥x轴于点E,如图,
∵ ∠ABD=45°,AD⊥AB,
∴ △ABD是等腰直角三角形,
∴ AB=AD,
∵ ∠BAD=90°,
∴ ∠OAB+∠EAD=90°,
∵ ∠OAB+∠OBA=90°,
∴ ∠EAD=∠OBA,
∵ ∠AOB=∠DEA=90°,
∴ △AOB≌△DEA(AAS),
∴ DE=AO,AE=BO,
∵ y=2x-2,
∴ A(1,0),B(0,-2),
∴ OA=1,OB=2,
∴ D(3,-1),
设BC的函数表达式为y=kx+b,
∴,
∴ k=,b=-2,
∴ y=x-2.
故答案为: y=x-2.
过点A作AD⊥BC于点D,过点D作DE⊥x轴于点E,根据等腰直角三角形的判定和性质可得AB=AD,证明出∠EAD=∠OBA,根据AAS判定△AOB≌△DEA推出 DE=AO,AE=BO,从而得到D点坐标,根据待定系数法,即可求得.
17.或
解:∵和都是等腰三角形,且,顶角,
∴FD=ED,∠CAB=72°,∠FDE=36°,∠EAD=108°,
由旋转得GD=AD,∠GDA=36°,
∴∠FDG=∠EDA,
易证△FDG≌△EDA(SAS),
∴∠FGD=∠EAD=108°,GF=EA,
当GF=EG时,如图所示:
易证△FGD≌△EGD(SSS),
∴∠EGD=108°,
∴∠FGE=144°;
当GF=EF时,如图所示:
∵GD=AD,∠GDA=36°,
∴∠AGD=∠GAD=72°,
∴∠FGD+∠AGD=180°,∠EAG=36°,
∴A、F、G共线,
∵GF=EF,GF=EA,
∴EF=EA,
∴∠EFG=∠EAG=36°,
∴∠FGE=72°,
综上所述,或,
故答案为:或
先根据三角形全等的性质结合等腰三角形的性质即可得到FD=ED,∠CAB=72°,∠FDE=36°,∠EAD=108°,进而根据旋转的性质得到GD=AD,∠GDA=36°,从而得到∠FDG=∠EDA,再根据三角形全等的判定与性质证明△FDG≌△EDA(SAS)即可得到∠FGD=∠EAD=108°,GF=EA,分类讨论:当GF=EG时,易证△FGD≌△EGD(SSS),进而结合题意即可求解;当GF=EF时,根据等腰三角形的性质结合题意得到∠AGD=∠GAD=72°,∠FGD+∠AGD=180°,∠EAG=36°,进而得到A、F、G共线,再根据等腰三角形的性质结合题意即可求解。
18.①②④
解:① 一次函数 ,由表格数据知:当y=0时x=2,
∴ 方程的解为 ,故①正确;
② 若,则一次函数经过一、二、四象限,
∴m<0,n>0,
∴,故②正确;
③由y=0.5x-1中,当y=0时,x=2,
∴直线y=0.5x-1与都经过(2,0),
由图象可知:当x>2时,直线y=0.5x-1的图象在直线图象的上方,
∴m>-1,故③错误;
④∵ 关于的不等式的解集为 ,
∴直线与y=x的交点为(,),
把(2,0)(,)代入中,得,
解得:m=-2,故④正确;
故答案为:①②④.
由表格知数据直接判断①;由可知一次函数经过一、二、四象限,据此确定m、n的符号,据此判断②;当x>2时,直线y=0.5x-1的图象在直线图象的上方,可确定m>-1,据此判断③;由关于的不等式的解集为 ,可确定直线与y=x的交点为(,),利用待定系数法求出m值,即可判断④.
19.(1)解:
=
=
=;
(2)解:
.
(1)运用有理数的乘方、二次根式的混合运算、立方根进行运算,再合并同类项即可求解;
(2)运用直接开平方法解一元二次方程即可求解。
20.
21.(1)解:见解析,即为所求;
(2)解:的面积
;
(3)解:见解析,点即为所求.
解:(1)如图,即为所求作的三角形;
(2);
(3)先作出点A关于y轴的对称点,连接交y轴于一点,该点即为所求作的点P,如图所示:
∵点A关于y轴的对称点,
∴,
∴,
∵两点之间线段最短,
∴此时的周长最小.
(1)先根据轴对称的性质作出点A、B、C关于x轴的对称点、、,然后顺次连接即可;
(2)利用坐标与距离的关系,结合三角形的面积公式,采用割补法求出的面积即可;
(3)先作出点A关于y轴的对称点,连接交y轴于一点,即为点P.
22.(1)解:∵,,,
∴,
∴为直角三角形,,
∴的面积.
(2)解:如下图,连接,
由折叠可知,,
即,
∴垂直平分,
∴,
设,则,
在中,有,
即,解得,
∴,
∴在中,可有,
即折痕的长为.
(1)先利用勾股定理的逆定理证出为直角三角形,,再利用三角形的面积公式求解即可;
(2)连接BD,设,则,利用勾股定理可得,即,解得,再求出BD的长,最后利用勾股定理求出DE的长即可.
23.(1)答案见试题解析;(2)答案见试题解析.
24.(1)解:∵点C的横坐标为1
∴当x=1时,
∴C(1,3)
∵A(-2,6)
∴有
解得:
(2)<1
(3)解:设D(0,m)
由(1)知:
取,则,解得∴B(4,0)
∵
∴
解得:∴
∵∴
∴点D的坐标为(0,-4)
解:(2)由(1)可知y1=-x+4,
解之:,
∴点C(1,3),
由图象可知当x<1时y1>y2.
故答案为:<1
(1)由点C的横坐标可求出点C的坐标,利用点A,C的坐标可求出k,b的值.
(2)将两函数解析式联立方程组,可求出点C的坐标,利用点C的横坐标可求出y1>y2时x的取值范围.
(3)设D(0,m)(m<0),利用函数解析式求出点B的坐标,根据 可得到关于m的方程,解方程求出m的值,可得到点D的坐标.
25.10或12.5千米
26.(1)1;或11
(2)解:该函数图象如图:
(3)解:①;或;根据(2)图象可直接看出,当或时,.
解:
(1) ① 当x=4时,y=a=,∴ a=1
②若为该函数图象上的点, 当x=b时,y=8.代入得:,解得b=-9或b=11
∴ b=-9或11
(2)画函数图象的步骤:列表,描点,连线。
(3) ① 由(2)图象可知,当x=1时,函数最小值为-2
② 当y≥0时,x≤-1或x≥3
本题考查函数图象和性质。根据表格中自变量x的值和因变量y的值,可画出函数图象,可得函数的最小值,找出函数和一次不等式的关系。
同课章节目录
