2024-2025学年浙教版八年级数学上册期末模拟卷(含答案+解析)
文档属性
| 名称 | 2024-2025学年浙教版八年级数学上册期末模拟卷(含答案+解析) |  | |
| 格式 | docx | ||
| 文件大小 | 596.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-09 21:14:12 | ||
图片预览




文档简介
保密★启用前
20224-2025学年八年级上册期末模拟卷(浙教版)
数学
考试范围:八上全册 考试时间:100分钟
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
一、单选题
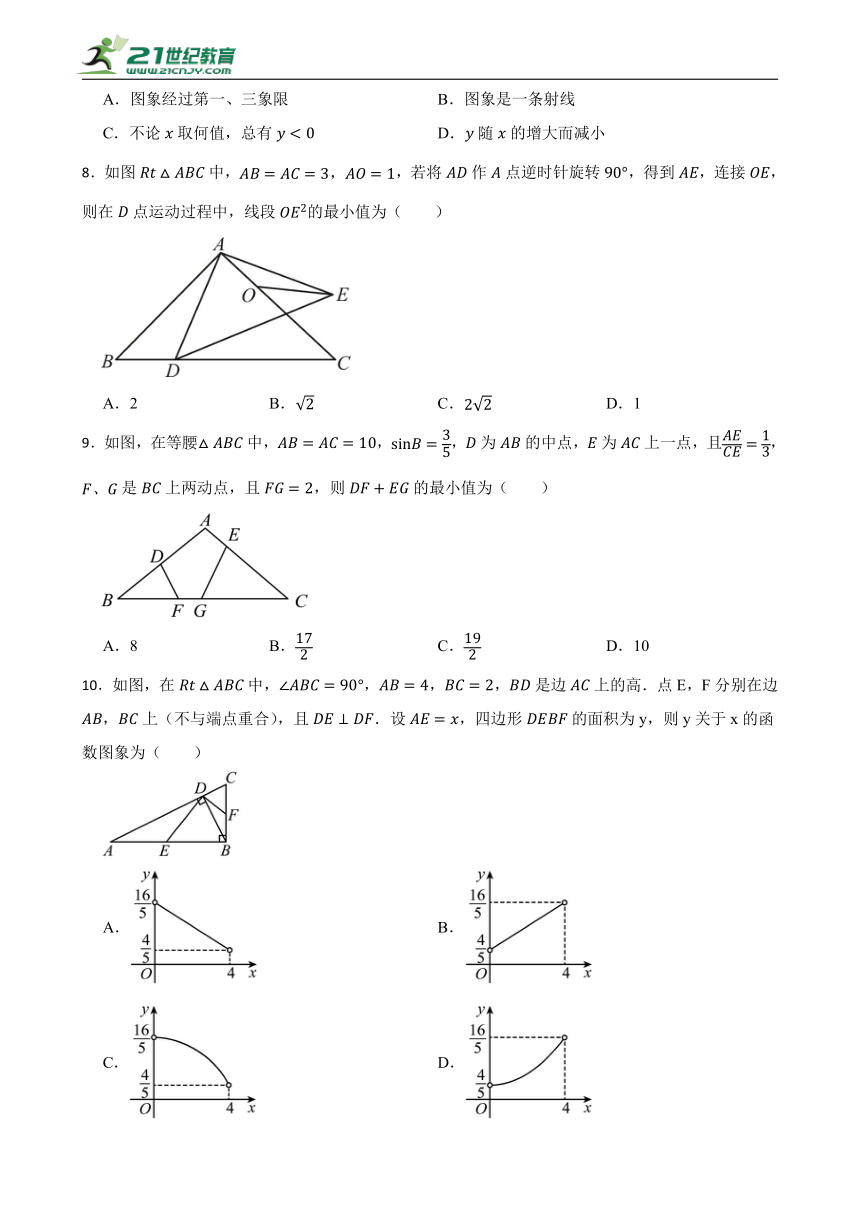
1.下列图标中,既是轴对称图形又是中心对称图形的是( )
A.宇航员 B.空间站
C.黑洞 D.太空舱
2. 下列说法正确的是( )
A. B.
C.是4的平方根 D.
3.如图,P,Q是△ABC的边BC上的两点,并且BP=PQ=QC=AP=AQ,则∠BAC的度数是( )
A.100° B.110° C.120° D.150°
4.下列命题的逆命题是假命题的是( )
A.等腰三角形的两个底角相等 B.全等三角形的对应边都相等
C.两直线平行,同旁内角互补 D.对顶角相等
5.已知关于的一元二次方程有实数根,则的取值范围是( )
A.且 B.且 C. D.
6.已知 则x+y的值为( )
A. B. C. D.
7.已知正比例函数,下列结论正确的是( )
A.图象经过第一、三象限 B.图象是一条射线
C.不论取何值,总有 D.随的增大而减小
8.如图中,,若将作点逆时针旋转,得到,连接,则在点运动过程中,线段的最小值为( )
A.2 B. C. D.1
9.如图,在等腰中,,,为的中点,为上一点,且,是上两动点,且,则的最小值为( )
A.8 B. C. D.10
10.如图,在中,,,,是边上的高.点E,F分别在边,上(不与端点重合),且.设,四边形的面积为y,则y关于x的函数图象为( )
A. B.
C. D.
二、填空题
11.已知2y+1与3x-3成正比例,且x=10时,y=4,则y与x的关系式是 .
12. 如图,一张矩形纸片 中, 点 在 边上, 把 沿直线 折叠, 使点 落在对角线 上的点 处.点 在 边上,把 沿直线 折叠,使点 落在线段 上的点 处. 若 , 则 , 矩形 的面积
13.如果是两个不相等的实数,且满足,那么代数式= .
14.如图,在△ABC中,CP平分∠ACB,AP⊥CP于点P,已知△ABC的面积为12cm2,则阴影部分的面积为 cm2.
15.若关于的不等式组至少有三个整数解,且关于的分式方程的解是非负整数,则符合条件的所有整数的和是 .
16.如图,在等腰中,,,点是边上一动点,将线段绕点顺时针旋转,得到线段,连接, ,则的最小值是 .
三、解答题
17. 计算:
(1)
18.解方程:
(1);
.
;
(4).
19.解方程和不等式组:
(1)解方程: ;
(2)解不等式组: 并把解集在数轴上表示出来.
20.如图,绕点旋转后能与重合.
(1),,求的长;
(2)延长交于点,,求的度数.
21.在九年级迎战体考的氛围带动下,某校八年级同学对体育锻炼越来越重视,同学们在八上期末、八下开学、八下半期举行的三次体育测试中获得满分的人数逐渐增多,从八上期末的150人满分,到八下半期满分人数上升至216人.
(1)如果每次测试满分人数增加的百分率相同,求这个百分率;
(2)已知体测满分50分,该年级共700名学生,其中有10名同学因身体原因每次测试只能得到35分.年级计划通过一系列举措,力争在八下期末测试时满分人数比八下半期满分人数增加.那么除了满分同学和10名因身体原因同学之外,其余同学至少平均多少分,才能使全年级平均分不低于46分?(结果精确到0.1)
22.如图,菱形中,为对角线,点E,F分别在上,,连接.
(1)求证:;
(2)连接交于点O,若E为中点,,求的长.
23.如图,在锐角△ABC中,点E是AB边上一点,BE=CE,AD⊥BC于点D,AD与EC交于点G.
(1)求证:△AEG是等腰三角形.
(2)若BE=10,CD=3,G为CE中点,求AG的长.
24.如图1,等腰直角三角形中,,直线经过点C,过点A作于点D,过点B作于点E,可以证明,我们将这个模型称为“一线三直角”.接下来我们就利用这个模型来解决一些问题:
(1)如图2,将一块等腰直角三角板放置在平面直角坐标系中,,点A在y轴的正半轴上,点C在x轴的负半轴上,点B在第二象限,点A坐标为,C的坐标为,则点B的坐标为_______;
(2)如图3,在平面直角坐标系中,等腰,与y轴交点D,点C的坐标为,A点的坐标为,求点B的坐标.
(3)如图4,等腰,,当点C在x轴正半轴上运动,点在y轴正半轴上运动,点在第四象限时,作轴于点D,请直接写出a,m,n之间的关系.
25.如图,在平面直角坐标系中,一次函数(m为常数)的图象交y轴于点,交x轴于点C,点A的坐标为,过点A作,且,连接.
(1)求m的值和点D的坐标.
(2)求直线的解析式.
(3)东东设计了一个小程序:动点P从点D出发在线段上向点A运动,速度为每秒2个单位长度,同时动点Q从点B出发在线段上向点C运动,速度为每秒个单位长度,点Q到达点C后程序结束,设程序运行时间为t秒,当与四边形的边平行时程序会发出警报声,求发出警报声时t的值.
答案解析部分
1.D
2.C
解:A:,A不符合题意;
B:,B不符合题意;
C:是4的平方根,C符合题意;
D:,D不符合题意;
故答案为:C
根据平方根、立方根结合题意对选项逐一分析即可求解。
3.C
解:∵AP=AQ=PQ,
∴△APQ是等边三角形,
∴∠APQ=∠AQP=60°,
∵BP=AP,AQ=CQ,
∴∠B=∠BAP,∠C=∠CAQ,
∴∠APQ=∠B+∠BAP=2∠B=60°,∠AQP=∠C+∠CAQ=2∠C=60°
∴∠B=30°,∠C=30°,
∴∠BAC=180°-∠B-∠C=120°.
故答案为:C.
由三边相等的三角形是等边三角形得△APQ是等边三角形,由等边三角形的每一个内角都等于60°得∠APQ=∠AQP=60°,由等边对等角及三角形外角性质得∠APQ=∠B+∠BAP=2∠B=60°,∠AQP=∠C+∠CAQ=2∠C=60°,从而可求出∠B与∠C的度数,最后根据三角形的内角和定理可算出∠BAC的度数.
4.D
解:A、等腰三角形的两个底角相等的逆命题:两个角相等的三角形是等腰三角形,是真命题,故不符合题意;
B、全等三角形的对应边都相等的逆命题:三边对应相等的两个三角形全等,是真命题,故不符合题意;
C、两直线平行,同旁内角互补的逆命题:同旁内角互补,两直线平行,是真命题,故不符合题意;
D、对顶角相等的逆命题:如果两个角相等,那么这两个角是对顶角,是假命题,故符合题意.
故答案为:D.
一个命题包括题设与结论两部分,将一个命题的题设与结论互换位置即可得出原命题的逆命题,据此先写出各项命题的逆命题,再根据等腰三角形的判定、全等三角形的判定,平行线的判定、对顶角的性质分别判断即可.
5.A
6.B
解: ,
(2x-1)2+=0,
∵ (2x-1)2≥0,≥0,
∴ 2x-1=0,3y-2=0,
∴ x=0.5,y=,
∴ x+y=.
故答案为:B.
根据配方法可得(2x-1)2+=0,再根据平方的非负性和算术平方根的非负性可得x,y的值,即可求得.
7.D
解:A、,图象在第二、四象限,A不符合题意;
B、正比例函数的图象是一条直线,B不符合题意;
C、应为当时,,C不符合题意;
D、,随的增大而减小,D不符合题意;
故答案为:D
根据一次函数的图象与系数的关系结合一次函数的性质即可求解。
8.A
如图,在上截取,连接,
将绕点逆时针旋转得到,
,
,即,
在和中,
,
,
,
点在线段上运动,
当时,的值最小,即线段有最小值,
是等腰直角三角形,
,
,
是等腰直角三角形,
,,
,
由勾股定理得,
线段有最小值为2,
故答案为:A.
根据题意先求出,再利用全等三角形的判定与性质证明求解即可。
9.B
解:如下图,过点作于点,过点作交于,连接,
在Rt△ABH中,
∴
∴AH=6
∵AB=AC,
∴BH=CH=8
∵,
∴,
∵,
∴△AEM∽△ACH
∴,
∴,AM=1.5
∴
由轴对称的性质可得
∴KN=AM+MN-AK=1.5+9-3=7.5
∵FG=2
∴,
∴四边形为平行四边形,
∴
∴=DF+MF
作点关于直线的对称点,连接交AB于点D,
∴=DF+MF=DF+FN
∴当点在同一直线上时,取最小值,最小值等于的长度
过点D作DK⊥AN,垂足为K
∵D为AB的中点,DK∥BC
∴,
在中,
∴的最小值为.
故选:B.
先根据,求出BH,AH,再根据△AEM∽△ACH,得出对应边成比例,求出AM,ME,再得到四边形为平行四边形,从而得到=DF+MF,再根据将军饮马模型,作作点关于直线的对称点,连接交AB于点D,则=DF+MF=DF+FN,因此当点在同一直线上时,取最小值,最小值等于的长度,在中,利用勾股定理,求出DN即可.
10.A
解:过点D作DM⊥AB于点M,作DN⊥BC于点N,如下图:
∵,,,
∴,
∵是边上的高.
∴,
∴,
∵,,
∴,
∴,
解得:,
∴
∵DM⊥AB,∠ABC=90°,
∴DM//AB,
∴△ADM∽△ACB,
∴,即,
∴
∵DN//AB,
∴△CDN∽△CAB,
∴,即,
∴.
∵,,
∴,,
∴,
∴.
∵AE=x,
∴BF=0.5x.
∴
∵,
∴当时, ,
当时,.
故答案为:A.
过点D作DM⊥AB于点M,作DN⊥BC于点N,由勾股定理求出,根据等面积法求出,DM和DN的长,证明,由相似三角形的性质可求出的长,继而可得DC的长;再证明 △ADM∽△ACB和△CDN∽△CAB,分别由相似三角形的性质可得出求出DM和DN的长,证明,可得AE:BF=2,据此表示出BF的长,利用,表示出两个三角形的面积,代入数据可得关于x的一次函数的解析式,最后根据自变量的大小求出对应的函数值.
11.y=x-1
解:∵ 2y+1与3x-3成正比例,
∴可设 2y+1=k(3x-3),
∵x=10时,y=4,
∴2×4+1=k(3×10-3),
∴k=,
∴2y+1=(3x-3),
∴y=.
故答案为:y=.
根据 2y+1与3x-3成正比例,可设 2y+1=k(3x-3),根据x=10时,y=4,可求得k=,代入 2y+1=k(3x-3)中,整理即可得出y=.
12.29;420
解:设,
,
,
由折叠的性质可得,
四边形ABCD是矩形,
,
,
,解得,
,
.
故答案为:29;420.
设,利用折叠的性质可得,再通过勾股定理得到,解得,进而求得BD的长度及矩形的面积.
13.2033
14.6
解:延长AP交BC于Q,
∵ CP平分∠ACB
∴∠ACP=∠PCQ,
∵ AP⊥CP于点P,
∴∠APC=∠QPC,
又PC=PC,
∴△APC≌△QPC(AAS),
∴AP=PQ,
∴S△ABP=S△ABQ,S△APC=S△AQC,
∴S阴影部分=S△ABP+S△APC=(S△ABQ+S△AQC)=S△ABC=6( cm2).
故答案为:6.
先利用AAS证明△APC≌△QPC,再利用全等三角形的性质,证明AP=PQ,然后利用S阴影部分=S△ABP+S△APC求解.
15.10
16.
17.(1)解:原式
(2)解:原式
(1)先利用负整数指数幂、0指数幂和绝对值的性质化简,再计算即可;
(2)利用二次根式的混合运算的计算方法及步骤(①有括号先算括号内;②再算二次根式的乘除;③最后计算二次根式的加减法)分析求解即可.
18.(1)
(2)
(3)
(4)
19.(1)解:去分母,得:,
移项,得:,
合并同类项,得:,
系数化为1,得:,
检验:当时,,故是原方程的解;
(2)解:解不等式组:,
解不等式①,得:,
解不等式②,得:,
将不等式组的解集表示在数轴上如下:
故原不等式组.
(1)按照解分式方程的一般步骤进行求解即可,需注意检验求解方程是否为原方程的解;
(2)按照解不等式组的一般步骤进行求解并表示在数轴上即可,需注意不等式取等与数轴的表示.
20.(1)解:∵△ABC绕点A旋转后能与△ADE重合,
∴△ABC≌△ADE,
∴,
∴;
(2)解:∵△ABC≌△ADE,
∴,,
∵,,
∴.
(1)由题意易得△ABC≌△ADE,由全等三角形的对应边相等得,进而根据代入计算即可;
(2)由全等三角形的对应角相等得,,再根据三角形的一个外角等于与之不相邻的两个内角的和得,,从而可推出.
(1)解:由旋转的性质可得,
∴;
(2)解:由旋转的性质可得,,
∵,,
∴.
21.(1)
(2)43.7分
22.(1)证明:∵四边形是菱形,
∴平分,
∵,
∴,即,
∴;
(2)解:∵四边形是菱形,BD=4
∴,,
∵,
∴在中,,
∴,
∴,
∵E为中点,
∴.
(1)由菱形的性质得到平分,再证明,即可利用等腰三角形的三线合一定理证明;
(2)先由菱形的性质得到,,再解直角三角形求出,进而求出,则由直角三角形斜边上的中线的性质可得答案.
(1)证明:∵四边形是菱形,
∴平分,
∵,
∴,即,
∴;
(2)解:∵四边形是菱形,
∴,,
∵,
∴在中,,
∴,
∴,
∵E为中点,
∴.
23.(1)证明:∵AD⊥BC,
∴∠ADB=∠ADC=90°,
∴∠B+∠BAD=90°,∠DCG+∠DGC=90°,
∵EB=EC,
∴∠B=∠DCG,
∴∠BAD=∠DGC,
∵∠AGE=∠DGC,
∴∠BAD=∠AGE,
∴EA=EG,
∴△AEG是等腰三角形;
(2)解:过点E作EF⊥AG,垂足为F,
∴∠EFG=90°,
∵EA=EG,EF⊥AG,
∴AG=2FG,
∵G为CE中点,
∴EG=GC=EC,
∵EB=EC=10,
∴GC=EC=5,
∵∠EFG=∠CDG=90°,∠EGF=∠CGD,
∴△EFG≌△CDG(AAS),
∴FG=DG,
在Rt△CDG中,CD=3,
∴DG==4,
∴FG=DG=4,
∴AG=2FG=8,
∴AG的长为8.
(1)根据垂直的概念可得∠ADB=∠ADC=90°,由等腰三角形的性质可得∠B=∠DCG,根据等角的余角相等可得∠BAD=∠DGC,由对顶角的性质可得∠AGE=∠DGC,则∠BAD=∠AGE,推出EA=EG,据此证明;
(2)过点E作EF⊥AG,垂足为F,根据等腰三角形的性质可得AG=2FG,由中点的概念可得EG=GC=EC=5,利用AAS证明△EFG≌△CDG,得到FG=DG,由勾股定理可得DG,据此求解.
24.(1)解:过点B作交直线于点D,如图,
∴∠BDC=90°,
∴∠DBC+∠BCD=90°,
∵∠AOC=90°,
∴∠BDC=∠AOC,
∵∠ACB=90°,
∴∠BCD+∠ACO=90°,
∴∠ACO=∠DBC,
在和中,
,
∴,
∴,
∵点A坐标为,C的坐标为,
∴,
∴,
∴点B的坐标为,
故答案为:;
(2)解:过点B作轴交y轴于点E,如图,
∵∠AOC=∠ACB=90°,
∴,
∴,,
∴,
在和中,
,
∵,
∴,
∵点C的坐标为,A点的坐标为,
∴,
∴
∴,
∴点B的坐标;
(3)解:过点B作轴交x轴于点E,如图,
则,
∵点在y轴正半轴上运动,点在第四象限,
∴,,
同理可证,,
∴,
∵,
∴,
∴.
(1)过点B作交直线于点D,利用“一线三垂直”全等三角形模型可证明,从而得,结合点A、C的坐标得,根据即可求得点B坐标;
(2)过点B作轴交y轴于点E,同理利用“一线三垂直”全等三角形模型可证明,结合点A、C的坐标得根据即可求得点B坐标;
(3)过点B作轴交x轴于点E,则,根据点坐标得,,同理可证,,则,结合即可求得关系式.
(1)解:过点B作交直线于点D,如图,
∵,,,
∴,
∴,
∵点A坐标为,C的坐标为,
∴,
∴,
则点B的坐标为,
故答案为:;
(2)解:过点B作交于点E,如图,
∵点C的坐标为,A点的坐标为,
∴,
∵,
∴,,
∴,
∵,
∴,
∴
则,
那么,点B的坐标;
(3)解:过点B作交于点E,如图,
则,
∵点在y轴正半轴上运动,点在第四象限,
∴,,
同理可证,,
∴,
∵,
∴,
则.
25.(1)解:∵一次函数的图象交y轴于点,
,
,
令,则,
,点C的坐标为,
,
,
,
点A的坐标为,,
,
∴点D的坐标为;
(2)解:设直线的解析式为,
将点和点代入中,
得,
解得,
∴直线的解析式为;
(3)解:由题意得点.
在中,.
如图,过点Q作于点M.
∴,
,
,
,
,
∵点Q在BC上运动,
,
①当时,设的解析式为,
将和代入中,
得,
解得,
即秒时,程序会发出警报声;
②当时,,
即,解得,
即秒时,程序会发出警报声,
综上,发出警报时t的值为2或4.
(1)将点B代入一次函数可求得m,再求出点C和OC,根据 ,可得AD=12,,由点A的坐标为,,,则点D的坐标为;
(2)设直线的解析式为, 利用待定系数法可求得直线的解析式;
(3)由题意得点,利用勾股定理可得BC,过点Q作于点M,证明,,,则,由点Q在BC上运动可知,分为两种情况求解: ①当时, ②当时 。
20224-2025学年八年级上册期末模拟卷(浙教版)
数学
考试范围:八上全册 考试时间:100分钟
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
一、单选题
1.下列图标中,既是轴对称图形又是中心对称图形的是( )
A.宇航员 B.空间站
C.黑洞 D.太空舱
2. 下列说法正确的是( )
A. B.
C.是4的平方根 D.
3.如图,P,Q是△ABC的边BC上的两点,并且BP=PQ=QC=AP=AQ,则∠BAC的度数是( )
A.100° B.110° C.120° D.150°
4.下列命题的逆命题是假命题的是( )
A.等腰三角形的两个底角相等 B.全等三角形的对应边都相等
C.两直线平行,同旁内角互补 D.对顶角相等
5.已知关于的一元二次方程有实数根,则的取值范围是( )
A.且 B.且 C. D.
6.已知 则x+y的值为( )
A. B. C. D.
7.已知正比例函数,下列结论正确的是( )
A.图象经过第一、三象限 B.图象是一条射线
C.不论取何值,总有 D.随的增大而减小
8.如图中,,若将作点逆时针旋转,得到,连接,则在点运动过程中,线段的最小值为( )
A.2 B. C. D.1
9.如图,在等腰中,,,为的中点,为上一点,且,是上两动点,且,则的最小值为( )
A.8 B. C. D.10
10.如图,在中,,,,是边上的高.点E,F分别在边,上(不与端点重合),且.设,四边形的面积为y,则y关于x的函数图象为( )
A. B.
C. D.
二、填空题
11.已知2y+1与3x-3成正比例,且x=10时,y=4,则y与x的关系式是 .
12. 如图,一张矩形纸片 中, 点 在 边上, 把 沿直线 折叠, 使点 落在对角线 上的点 处.点 在 边上,把 沿直线 折叠,使点 落在线段 上的点 处. 若 , 则 , 矩形 的面积
13.如果是两个不相等的实数,且满足,那么代数式= .
14.如图,在△ABC中,CP平分∠ACB,AP⊥CP于点P,已知△ABC的面积为12cm2,则阴影部分的面积为 cm2.
15.若关于的不等式组至少有三个整数解,且关于的分式方程的解是非负整数,则符合条件的所有整数的和是 .
16.如图,在等腰中,,,点是边上一动点,将线段绕点顺时针旋转,得到线段,连接, ,则的最小值是 .
三、解答题
17. 计算:
(1)
18.解方程:
(1);
.
;
(4).
19.解方程和不等式组:
(1)解方程: ;
(2)解不等式组: 并把解集在数轴上表示出来.
20.如图,绕点旋转后能与重合.
(1),,求的长;
(2)延长交于点,,求的度数.
21.在九年级迎战体考的氛围带动下,某校八年级同学对体育锻炼越来越重视,同学们在八上期末、八下开学、八下半期举行的三次体育测试中获得满分的人数逐渐增多,从八上期末的150人满分,到八下半期满分人数上升至216人.
(1)如果每次测试满分人数增加的百分率相同,求这个百分率;
(2)已知体测满分50分,该年级共700名学生,其中有10名同学因身体原因每次测试只能得到35分.年级计划通过一系列举措,力争在八下期末测试时满分人数比八下半期满分人数增加.那么除了满分同学和10名因身体原因同学之外,其余同学至少平均多少分,才能使全年级平均分不低于46分?(结果精确到0.1)
22.如图,菱形中,为对角线,点E,F分别在上,,连接.
(1)求证:;
(2)连接交于点O,若E为中点,,求的长.
23.如图,在锐角△ABC中,点E是AB边上一点,BE=CE,AD⊥BC于点D,AD与EC交于点G.
(1)求证:△AEG是等腰三角形.
(2)若BE=10,CD=3,G为CE中点,求AG的长.
24.如图1,等腰直角三角形中,,直线经过点C,过点A作于点D,过点B作于点E,可以证明,我们将这个模型称为“一线三直角”.接下来我们就利用这个模型来解决一些问题:
(1)如图2,将一块等腰直角三角板放置在平面直角坐标系中,,点A在y轴的正半轴上,点C在x轴的负半轴上,点B在第二象限,点A坐标为,C的坐标为,则点B的坐标为_______;
(2)如图3,在平面直角坐标系中,等腰,与y轴交点D,点C的坐标为,A点的坐标为,求点B的坐标.
(3)如图4,等腰,,当点C在x轴正半轴上运动,点在y轴正半轴上运动,点在第四象限时,作轴于点D,请直接写出a,m,n之间的关系.
25.如图,在平面直角坐标系中,一次函数(m为常数)的图象交y轴于点,交x轴于点C,点A的坐标为,过点A作,且,连接.
(1)求m的值和点D的坐标.
(2)求直线的解析式.
(3)东东设计了一个小程序:动点P从点D出发在线段上向点A运动,速度为每秒2个单位长度,同时动点Q从点B出发在线段上向点C运动,速度为每秒个单位长度,点Q到达点C后程序结束,设程序运行时间为t秒,当与四边形的边平行时程序会发出警报声,求发出警报声时t的值.
答案解析部分
1.D
2.C
解:A:,A不符合题意;
B:,B不符合题意;
C:是4的平方根,C符合题意;
D:,D不符合题意;
故答案为:C
根据平方根、立方根结合题意对选项逐一分析即可求解。
3.C
解:∵AP=AQ=PQ,
∴△APQ是等边三角形,
∴∠APQ=∠AQP=60°,
∵BP=AP,AQ=CQ,
∴∠B=∠BAP,∠C=∠CAQ,
∴∠APQ=∠B+∠BAP=2∠B=60°,∠AQP=∠C+∠CAQ=2∠C=60°
∴∠B=30°,∠C=30°,
∴∠BAC=180°-∠B-∠C=120°.
故答案为:C.
由三边相等的三角形是等边三角形得△APQ是等边三角形,由等边三角形的每一个内角都等于60°得∠APQ=∠AQP=60°,由等边对等角及三角形外角性质得∠APQ=∠B+∠BAP=2∠B=60°,∠AQP=∠C+∠CAQ=2∠C=60°,从而可求出∠B与∠C的度数,最后根据三角形的内角和定理可算出∠BAC的度数.
4.D
解:A、等腰三角形的两个底角相等的逆命题:两个角相等的三角形是等腰三角形,是真命题,故不符合题意;
B、全等三角形的对应边都相等的逆命题:三边对应相等的两个三角形全等,是真命题,故不符合题意;
C、两直线平行,同旁内角互补的逆命题:同旁内角互补,两直线平行,是真命题,故不符合题意;
D、对顶角相等的逆命题:如果两个角相等,那么这两个角是对顶角,是假命题,故符合题意.
故答案为:D.
一个命题包括题设与结论两部分,将一个命题的题设与结论互换位置即可得出原命题的逆命题,据此先写出各项命题的逆命题,再根据等腰三角形的判定、全等三角形的判定,平行线的判定、对顶角的性质分别判断即可.
5.A
6.B
解: ,
(2x-1)2+=0,
∵ (2x-1)2≥0,≥0,
∴ 2x-1=0,3y-2=0,
∴ x=0.5,y=,
∴ x+y=.
故答案为:B.
根据配方法可得(2x-1)2+=0,再根据平方的非负性和算术平方根的非负性可得x,y的值,即可求得.
7.D
解:A、,图象在第二、四象限,A不符合题意;
B、正比例函数的图象是一条直线,B不符合题意;
C、应为当时,,C不符合题意;
D、,随的增大而减小,D不符合题意;
故答案为:D
根据一次函数的图象与系数的关系结合一次函数的性质即可求解。
8.A
如图,在上截取,连接,
将绕点逆时针旋转得到,
,
,即,
在和中,
,
,
,
点在线段上运动,
当时,的值最小,即线段有最小值,
是等腰直角三角形,
,
,
是等腰直角三角形,
,,
,
由勾股定理得,
线段有最小值为2,
故答案为:A.
根据题意先求出,再利用全等三角形的判定与性质证明求解即可。
9.B
解:如下图,过点作于点,过点作交于,连接,
在Rt△ABH中,
∴
∴AH=6
∵AB=AC,
∴BH=CH=8
∵,
∴,
∵,
∴△AEM∽△ACH
∴,
∴,AM=1.5
∴
由轴对称的性质可得
∴KN=AM+MN-AK=1.5+9-3=7.5
∵FG=2
∴,
∴四边形为平行四边形,
∴
∴=DF+MF
作点关于直线的对称点,连接交AB于点D,
∴=DF+MF=DF+FN
∴当点在同一直线上时,取最小值,最小值等于的长度
过点D作DK⊥AN,垂足为K
∵D为AB的中点,DK∥BC
∴,
在中,
∴的最小值为.
故选:B.
先根据,求出BH,AH,再根据△AEM∽△ACH,得出对应边成比例,求出AM,ME,再得到四边形为平行四边形,从而得到=DF+MF,再根据将军饮马模型,作作点关于直线的对称点,连接交AB于点D,则=DF+MF=DF+FN,因此当点在同一直线上时,取最小值,最小值等于的长度,在中,利用勾股定理,求出DN即可.
10.A
解:过点D作DM⊥AB于点M,作DN⊥BC于点N,如下图:
∵,,,
∴,
∵是边上的高.
∴,
∴,
∵,,
∴,
∴,
解得:,
∴
∵DM⊥AB,∠ABC=90°,
∴DM//AB,
∴△ADM∽△ACB,
∴,即,
∴
∵DN//AB,
∴△CDN∽△CAB,
∴,即,
∴.
∵,,
∴,,
∴,
∴.
∵AE=x,
∴BF=0.5x.
∴
∵,
∴当时, ,
当时,.
故答案为:A.
过点D作DM⊥AB于点M,作DN⊥BC于点N,由勾股定理求出,根据等面积法求出,DM和DN的长,证明,由相似三角形的性质可求出的长,继而可得DC的长;再证明 △ADM∽△ACB和△CDN∽△CAB,分别由相似三角形的性质可得出求出DM和DN的长,证明,可得AE:BF=2,据此表示出BF的长,利用,表示出两个三角形的面积,代入数据可得关于x的一次函数的解析式,最后根据自变量的大小求出对应的函数值.
11.y=x-1
解:∵ 2y+1与3x-3成正比例,
∴可设 2y+1=k(3x-3),
∵x=10时,y=4,
∴2×4+1=k(3×10-3),
∴k=,
∴2y+1=(3x-3),
∴y=.
故答案为:y=.
根据 2y+1与3x-3成正比例,可设 2y+1=k(3x-3),根据x=10时,y=4,可求得k=,代入 2y+1=k(3x-3)中,整理即可得出y=.
12.29;420
解:设,
,
,
由折叠的性质可得,
四边形ABCD是矩形,
,
,
,解得,
,
.
故答案为:29;420.
设,利用折叠的性质可得,再通过勾股定理得到,解得,进而求得BD的长度及矩形的面积.
13.2033
14.6
解:延长AP交BC于Q,
∵ CP平分∠ACB
∴∠ACP=∠PCQ,
∵ AP⊥CP于点P,
∴∠APC=∠QPC,
又PC=PC,
∴△APC≌△QPC(AAS),
∴AP=PQ,
∴S△ABP=S△ABQ,S△APC=S△AQC,
∴S阴影部分=S△ABP+S△APC=(S△ABQ+S△AQC)=S△ABC=6( cm2).
故答案为:6.
先利用AAS证明△APC≌△QPC,再利用全等三角形的性质,证明AP=PQ,然后利用S阴影部分=S△ABP+S△APC求解.
15.10
16.
17.(1)解:原式
(2)解:原式
(1)先利用负整数指数幂、0指数幂和绝对值的性质化简,再计算即可;
(2)利用二次根式的混合运算的计算方法及步骤(①有括号先算括号内;②再算二次根式的乘除;③最后计算二次根式的加减法)分析求解即可.
18.(1)
(2)
(3)
(4)
19.(1)解:去分母,得:,
移项,得:,
合并同类项,得:,
系数化为1,得:,
检验:当时,,故是原方程的解;
(2)解:解不等式组:,
解不等式①,得:,
解不等式②,得:,
将不等式组的解集表示在数轴上如下:
故原不等式组.
(1)按照解分式方程的一般步骤进行求解即可,需注意检验求解方程是否为原方程的解;
(2)按照解不等式组的一般步骤进行求解并表示在数轴上即可,需注意不等式取等与数轴的表示.
20.(1)解:∵△ABC绕点A旋转后能与△ADE重合,
∴△ABC≌△ADE,
∴,
∴;
(2)解:∵△ABC≌△ADE,
∴,,
∵,,
∴.
(1)由题意易得△ABC≌△ADE,由全等三角形的对应边相等得,进而根据代入计算即可;
(2)由全等三角形的对应角相等得,,再根据三角形的一个外角等于与之不相邻的两个内角的和得,,从而可推出.
(1)解:由旋转的性质可得,
∴;
(2)解:由旋转的性质可得,,
∵,,
∴.
21.(1)
(2)43.7分
22.(1)证明:∵四边形是菱形,
∴平分,
∵,
∴,即,
∴;
(2)解:∵四边形是菱形,BD=4
∴,,
∵,
∴在中,,
∴,
∴,
∵E为中点,
∴.
(1)由菱形的性质得到平分,再证明,即可利用等腰三角形的三线合一定理证明;
(2)先由菱形的性质得到,,再解直角三角形求出,进而求出,则由直角三角形斜边上的中线的性质可得答案.
(1)证明:∵四边形是菱形,
∴平分,
∵,
∴,即,
∴;
(2)解:∵四边形是菱形,
∴,,
∵,
∴在中,,
∴,
∴,
∵E为中点,
∴.
23.(1)证明:∵AD⊥BC,
∴∠ADB=∠ADC=90°,
∴∠B+∠BAD=90°,∠DCG+∠DGC=90°,
∵EB=EC,
∴∠B=∠DCG,
∴∠BAD=∠DGC,
∵∠AGE=∠DGC,
∴∠BAD=∠AGE,
∴EA=EG,
∴△AEG是等腰三角形;
(2)解:过点E作EF⊥AG,垂足为F,
∴∠EFG=90°,
∵EA=EG,EF⊥AG,
∴AG=2FG,
∵G为CE中点,
∴EG=GC=EC,
∵EB=EC=10,
∴GC=EC=5,
∵∠EFG=∠CDG=90°,∠EGF=∠CGD,
∴△EFG≌△CDG(AAS),
∴FG=DG,
在Rt△CDG中,CD=3,
∴DG==4,
∴FG=DG=4,
∴AG=2FG=8,
∴AG的长为8.
(1)根据垂直的概念可得∠ADB=∠ADC=90°,由等腰三角形的性质可得∠B=∠DCG,根据等角的余角相等可得∠BAD=∠DGC,由对顶角的性质可得∠AGE=∠DGC,则∠BAD=∠AGE,推出EA=EG,据此证明;
(2)过点E作EF⊥AG,垂足为F,根据等腰三角形的性质可得AG=2FG,由中点的概念可得EG=GC=EC=5,利用AAS证明△EFG≌△CDG,得到FG=DG,由勾股定理可得DG,据此求解.
24.(1)解:过点B作交直线于点D,如图,
∴∠BDC=90°,
∴∠DBC+∠BCD=90°,
∵∠AOC=90°,
∴∠BDC=∠AOC,
∵∠ACB=90°,
∴∠BCD+∠ACO=90°,
∴∠ACO=∠DBC,
在和中,
,
∴,
∴,
∵点A坐标为,C的坐标为,
∴,
∴,
∴点B的坐标为,
故答案为:;
(2)解:过点B作轴交y轴于点E,如图,
∵∠AOC=∠ACB=90°,
∴,
∴,,
∴,
在和中,
,
∵,
∴,
∵点C的坐标为,A点的坐标为,
∴,
∴
∴,
∴点B的坐标;
(3)解:过点B作轴交x轴于点E,如图,
则,
∵点在y轴正半轴上运动,点在第四象限,
∴,,
同理可证,,
∴,
∵,
∴,
∴.
(1)过点B作交直线于点D,利用“一线三垂直”全等三角形模型可证明,从而得,结合点A、C的坐标得,根据即可求得点B坐标;
(2)过点B作轴交y轴于点E,同理利用“一线三垂直”全等三角形模型可证明,结合点A、C的坐标得根据即可求得点B坐标;
(3)过点B作轴交x轴于点E,则,根据点坐标得,,同理可证,,则,结合即可求得关系式.
(1)解:过点B作交直线于点D,如图,
∵,,,
∴,
∴,
∵点A坐标为,C的坐标为,
∴,
∴,
则点B的坐标为,
故答案为:;
(2)解:过点B作交于点E,如图,
∵点C的坐标为,A点的坐标为,
∴,
∵,
∴,,
∴,
∵,
∴,
∴
则,
那么,点B的坐标;
(3)解:过点B作交于点E,如图,
则,
∵点在y轴正半轴上运动,点在第四象限,
∴,,
同理可证,,
∴,
∵,
∴,
则.
25.(1)解:∵一次函数的图象交y轴于点,
,
,
令,则,
,点C的坐标为,
,
,
,
点A的坐标为,,
,
∴点D的坐标为;
(2)解:设直线的解析式为,
将点和点代入中,
得,
解得,
∴直线的解析式为;
(3)解:由题意得点.
在中,.
如图,过点Q作于点M.
∴,
,
,
,
,
∵点Q在BC上运动,
,
①当时,设的解析式为,
将和代入中,
得,
解得,
即秒时,程序会发出警报声;
②当时,,
即,解得,
即秒时,程序会发出警报声,
综上,发出警报时t的值为2或4.
(1)将点B代入一次函数可求得m,再求出点C和OC,根据 ,可得AD=12,,由点A的坐标为,,,则点D的坐标为;
(2)设直线的解析式为, 利用待定系数法可求得直线的解析式;
(3)由题意得点,利用勾股定理可得BC,过点Q作于点M,证明,,,则,由点Q在BC上运动可知,分为两种情况求解: ①当时, ②当时 。
同课章节目录
