2024-2025学年北师大版八年级数学上册期末押题卷(含答案+解析)
文档属性
| 名称 | 2024-2025学年北师大版八年级数学上册期末押题卷(含答案+解析) |  | |
| 格式 | docx | ||
| 文件大小 | 840.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-15 17:25:18 | ||
图片预览




文档简介
保密★启用前
20224-2025学年八年级上册期末押题卷(北师大版)
数学
考试范围:八上全册 考试时间:100分钟
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
一、单选题
1.定西剪纸是一种甘肃省的传统民间剪纸艺术,作为一种镂空艺术,它能给人以视觉上透空的感觉和艺术享受.下列作品中,是轴对称图形的是( )
A. B.
C. D.
2.下列运算正确的是( )
A. B.
C. D.
3.如图,AB=AD,点B关于AC的对称点E恰好落在CD上.若∠BAD=α(0°<a<180°),∠ACB=β,则下列关系正确的是( )
A.a﹣β=90° B.α+β=180°
C.c=3β D.a+2β=180°
4.下列命题的逆命题是假命题的是( )
A.等腰三角形的两个底角相等 B.全等三角形的对应边都相等
C.两直线平行,同旁内角互补 D.对顶角相等
5.关于的一元二次方程有实数根,则满足( )
A. B.且 C.且 D.
6.若,则的值为( )
A. B. C. D.
7.已知正比例函数,下列结论正确的是( )
A.图象经过第一、三象限 B.图象是一条射线
C.不论取何值,总有 D.随的增大而减小
8.如图中,,若将作点逆时针旋转,得到,连接,则在点运动过程中,线段的最小值为( )
A.2 B. C. D.1
9.如图,在平面直角坐标系中,菱形的顶点A在y轴的正半轴上,顶点B、C在x轴的正半轴上,,.点M在菱形的边和上运动(不与点A,C重合),过点M作轴,与菱形的另一边交于点N,连接,,设点M的横坐标为x,的面积为y,则下列图象能正确反映y与x之间函数关系的是( )
A. B.
C. D.
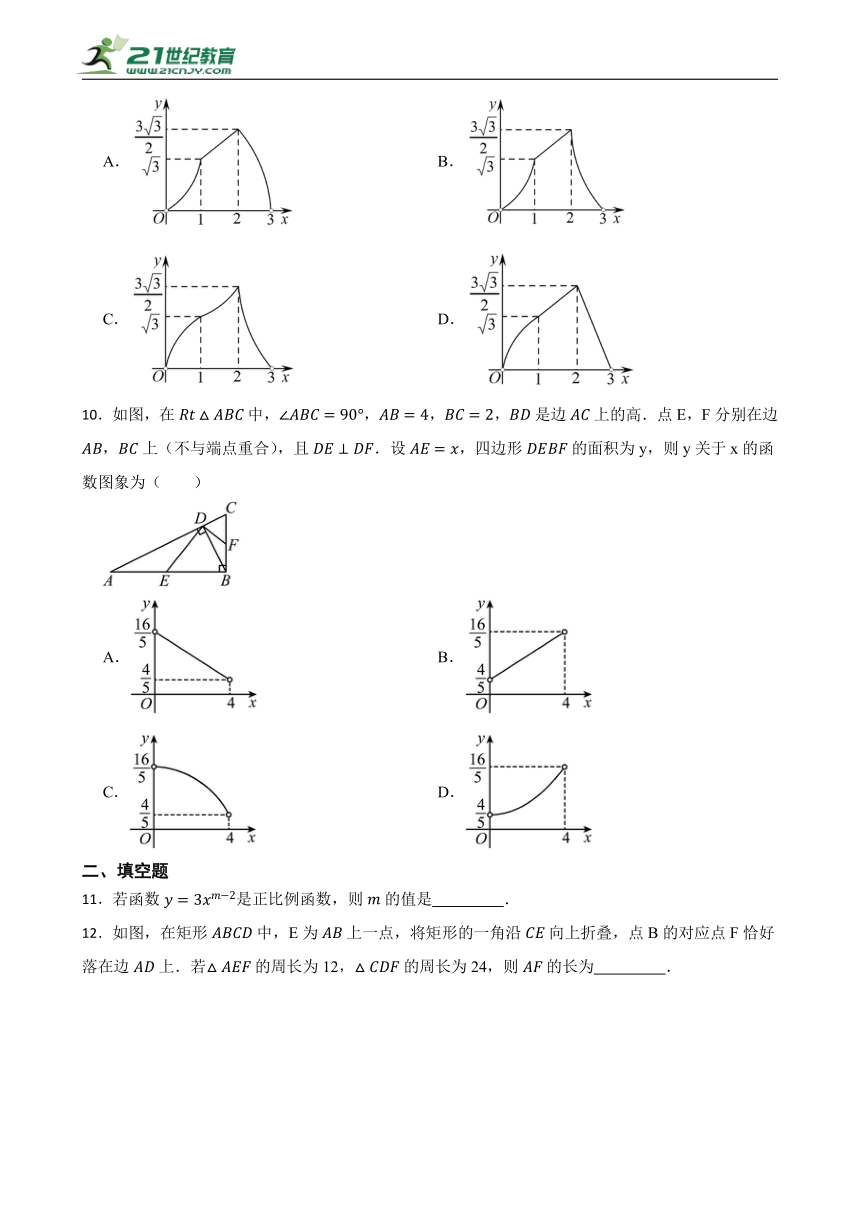
10.如图,在中,,,,是边上的高.点E,F分别在边,上(不与端点重合),且.设,四边形的面积为y,则y关于x的函数图象为( )
A. B.
C. D.
二、填空题
11.若函数是正比例函数,则的值是 .
12.如图,在矩形中,E为上一点,将矩形的一角沿向上折叠,点B的对应点F恰好落在边上.若的周长为12,的周长为24,则的长为 .
13.若,则的值是 .
14.如图,在△ABC中,CP平分∠ACB,AP⊥CP于点P,已知△ABC的面积为12cm2,则阴影部分的面积为 cm2.
15.若关于x的不等式组的解集为,关于y的分式方程有非负整数解,则符合条件的所有整数a的和为 .
16.如图,在等腰中,,,点是边上一动点,将线段绕点顺时针旋转,得到线段,连接, ,则的最小值是 .
三、解答题
17.计算:
(1);
.
18.解方程:
(1);
.
解不等式组,并把解集在数轴上表示出来.
20.如图,等边三角形中,D、E分别为边上的两动点,与交于点F,于点G,若,求的大小.
21.2023年10月,成都某景区就开始为冬季旅游做宣传,致使游客人数逐月增加. 10月份游客人数为万人,12月份游客人数为万人.若平均每月增长的百分率相同,请解答下列问题:
(1)求这两个月该景区游客人数的月平均增长率;
(2)预计今年1月份该景区游客人数会继续增长,已知该景区1月1日至1月4日已接待游客万人,则在1月份剩余天数中,该景区至少还需接待游客多少万人才能保证月平均增长率不降低?
22.如图,在中,,点D是边的中点,点O在边上,经过点C且与边相切于点E,.
(1)求证:是的切线;
(2)若,求的半径长.
23.如图,在四边形ABCD中,AB//DC,AB=AD,对角线AC,BD交于点O,AC平分∠BAD,过点C作CE⊥AB交AB的延长线于点E,连接OE。
(1)求证:四边形ABCD是菱形;
(2)若AB= ,BD=2,求OE的长.
24.如图1,等腰直角三角形中,,直线经过点C,过点A作于点D,过点B作于点E,可以证明,我们将这个模型称为“一线三直角”.接下来我们就利用这个模型来解决一些问题:
(1)如图2,将一块等腰直角三角板放置在平面直角坐标系中,,点A在y轴的正半轴上,点C在x轴的负半轴上,点B在第二象限,点A坐标为,C的坐标为,则点B的坐标为_______;
(2)如图3,在平面直角坐标系中,等腰,与y轴交点D,点C的坐标为,A点的坐标为,求点B的坐标.
(3)如图4,等腰,,当点C在x轴正半轴上运动,点在y轴正半轴上运动,点在第四象限时,作轴于点D,请直接写出a,m,n之间的关系.
25.如图,在平面直角坐标系中,直线与x轴、y轴分别交于A、B两点,过点B的直线交x轴与点
(1)点A坐标为 ,点B坐标为 ;
(2)求直线的表达式;
(3)若点D在直线上,且是以为腰的等腰三角形,点D的坐标.
答案解析部分
1.B
解:A、∵该图形不是轴对称,∴A不符合题意;
B、∵该图形是轴对称,∴B符合题意;
C、∵该图形不是轴对称,∴C不符合题意;
D、∵该图形不是轴对称,∴D不符合题意;
故答案为:B.
利用轴对称图形的定义(如果一个图形沿着一条直线对折后两部分完全重合,这样的图形叫做轴对称图形,这条直线叫做对称轴)逐项分析判断即可.
2.B
解:A、 ,故此项不符合题意;
B、 ,故此项符合题意;
C、与不是同类二次根式,不能合并,故此项不符合题意;
D、 ,故此项不符合题意;
故答案为:B.
根据二次根式的性质、积的乘方、二次根式的加减、有理数的加法分别计算,再判断即可.
3.D
解:∵点B关于AC的对称点E恰好落在CD上,
∴AB=AE,∠ACE=∠ACB,∠BAC=∠EAC,
∵AB=AD,
∴∠D=∠AED,
又∠AED=∠ACE+∠EAC,
∠DAE+∠D+∠AED=180°,
∴∠DAE+∠ACE+∠EAC+∠ACE+∠EAC=180°,
∴∠DAE+β+∠EAC+β+∠EAC=180°,
∴ α+2β=180°,
故答案为:D.
先利用“在同一个三角形,等边对等角”,证明∠D=∠AED,再利用三角形外角的性质,得出∠AED=∠ACE+∠EAC,再根据三角形内角和定理,得到∠DAE+∠D+∠AED=180°,转化为 α , β 表示的式子即可.
4.D
解:A、等腰三角形的两个底角相等的逆命题:两个角相等的三角形是等腰三角形,是真命题,故不符合题意;
B、全等三角形的对应边都相等的逆命题:三边对应相等的两个三角形全等,是真命题,故不符合题意;
C、两直线平行,同旁内角互补的逆命题:同旁内角互补,两直线平行,是真命题,故不符合题意;
D、对顶角相等的逆命题:如果两个角相等,那么这两个角是对顶角,是假命题,故符合题意.
故答案为:D.
一个命题包括题设与结论两部分,将一个命题的题设与结论互换位置即可得出原命题的逆命题,据此先写出各项命题的逆命题,再根据等腰三角形的判定、全等三角形的判定,平行线的判定、对顶角的性质分别判断即可.
5.C
解:∵ 一元二次方程有实数根,
∴,
解得:
故C正确,A、B、D错误,
故答案为:C.
由一元二次方程有实数根,故可知根的判别式大于或者等于零,且要注意a的取值不能使二次项系数为零,综合可知a的取值范围。
6.A
∵,
∴2a-4=0,b+1=0,
∴a=2,b=-1,
∴ab=2×(-1)=-2,
故答案为:A.
先利用非负数之和为0的性质求出a、b的值,再将a、b的值代入ab计算即可.
7.D
解:A、,图象在第二、四象限,A不符合题意;
B、正比例函数的图象是一条直线,B不符合题意;
C、应为当时,,C不符合题意;
D、,随的增大而减小,D不符合题意;
故答案为:D
根据一次函数的图象与系数的关系结合一次函数的性质即可求解。
8.A
如图,在上截取,连接,
将绕点逆时针旋转得到,
,
,即,
在和中,
,
,
,
点在线段上运动,
当时,的值最小,即线段有最小值,
是等腰直角三角形,
,
,
是等腰直角三角形,
,,
,
由勾股定理得,
线段有最小值为2,
故答案为:A.
根据题意先求出,再利用全等三角形的判定与性质证明求解即可。
9.A
10.A
解:过点D作DM⊥AB于点M,作DN⊥BC于点N,如下图:
∵,,,
∴,
∵是边上的高.
∴,
∴,
∵,,
∴,
∴,
解得:,
∴
∵DM⊥AB,∠ABC=90°,
∴DM//AB,
∴△ADM∽△ACB,
∴,即,
∴
∵DN//AB,
∴△CDN∽△CAB,
∴,即,
∴.
∵,,
∴,,
∴,
∴.
∵AE=x,
∴BF=0.5x.
∴
∵,
∴当时, ,
当时,.
故答案为:A.
过点D作DM⊥AB于点M,作DN⊥BC于点N,由勾股定理求出,根据等面积法求出,DM和DN的长,证明,由相似三角形的性质可求出的长,继而可得DC的长;再证明 △ADM∽△ACB和△CDN∽△CAB,分别由相似三角形的性质可得出求出DM和DN的长,证明,可得AE:BF=2,据此表示出BF的长,利用,表示出两个三角形的面积,代入数据可得关于x的一次函数的解析式,最后根据自变量的大小求出对应的函数值.
11.3
解:根据题意,得:m-2=1,
∴m=3.
故第一空答案为:3.
根据正比例函数的定义,直接列出方程m-2=1,解方程求出m的值即可。
12.4
解:四边形是矩形,
,,∠D=90°,
∵将矩形的一角沿向上折叠,点B的对应点F恰好落在边上,
∴,,
的周长为12,的周长为24,
,,
,
,
,,
在中,由勾股定理得,
,
∴,
,
,
故答案为:4.
由矩形和折叠的性质可知,,,,∠D=90°,再根据三角形周长,求得,,然后在中,利用勾股定理得的长,即可求出AF=AD-DF的长.
13.6
14.6
解:延长AP交BC于Q,
∵ CP平分∠ACB
∴∠ACP=∠PCQ,
∵ AP⊥CP于点P,
∴∠APC=∠QPC,
又PC=PC,
∴△APC≌△QPC(AAS),
∴AP=PQ,
∴S△ABP=S△ABQ,S△APC=S△AQC,
∴S阴影部分=S△ABP+S△APC=(S△ABQ+S△AQC)=S△ABC=6( cm2).
故答案为:6.
先利用AAS证明△APC≌△QPC,再利用全等三角形的性质,证明AP=PQ,然后利用S阴影部分=S△ABP+S△APC求解.
15.
16.
17.(1)解:原式
;
(2)解:原式
.
(1)利用二次根式的乘除法的计算方法及步骤(①先将除法转换为乘法;②再利用二次根式的乘法的计算方法计算)分析求解即可;
(2)先利用平方差公式和完全平方公式展开,再计算即可.
(1)解:原式
;
(2)解:原式
.
18.(1)
(2)
19.解:,
解不等式①得:,
解不等式②得:,
∴不等式组的解集为,
在数轴上表示为:
由题意先求出每一个不等式的解集,再找出各解集的公共部分即为不等式组的解集;在数轴上表示解集时,再根据“>”空心向右、“≤”实心向左即可求解.
20.解:∵等边三角形,
∴,,
∵,,,
∴,
∴,
∴,
∴,
∴,
∴的大小为.
本题考查等边三角形的性质,全等三角形的判定与性质,三角形外角的性质,三角形内角和定理.利用等边三角形的性质可得,,再结合,,,利用全等三角形的判定定理可证明,利用全等三角形的性质可得:,,,根据,代入数据可求出的大小.
21.(1)
(2)
22.(1)证明:如图,作,垂足为点H,连接,
∵,D是的中点,
∴,
∴,
∵,
又∵,
∴,
即是的平分线,
∵点O在上,与相切于点E,
∴,且是的半径,
∴,是的半径,
∴是的切线;
(2)解:在中,,
∴,
∵是的切线,
∴,
∴,
设的半径为r,则,
在中,由勾股定理得:,
∴,
∴.
∴的半径长为3.
(1)作,垂足为点H,连接,先证出,且是的半径,再结合,是的半径,即可证出是的切线;
(2)设的半径为r,则,利用勾股定理可得,再求出r的值即可.
(1)证明:如图,作,垂足为点H,连接,
∵,D是的中点,
∴,
∴,
∵,
又∵,
∴,
即是的平分线,
∵点O在上,与相切于点E,
∴,且是的半径,
∴,是的半径,
∴是的切线;
(2)解:在中,,
∴,
∵是的切线,
∴,
∴,
设的半径为r,则,
在中,由勾股定理得:,
∴,
∴.
∴的半径长为3.
23.(1)∵AB∥CD,∴∠OAB=∠DCA,
∵AC平分∠BAD,∴∠OAB=∠DAC,
∴CD=AD=AB,
∵AB∥CD,
∴四边形ABCD是平行四边形,
∵AD=AB,
∴平行四边形ABCD是菱形;
(2)解: ∵四边形ABCD是菱形,
∴OA=OC,BD⊥AC,BO=BD=1,
∴OA==2,
∴AC =2OA =4,
∵CE⊥AB,∴∠AEC=90°,
∴OE=AC=2.
(1)由平行线的性质得出∠OAB=∠DCA,由角平分线的定义得出∠OAB=∠DAC,利用等角对等边可得CD=AD=AB,结合AB∥CD,即证四边形ABCD是菱形;
(2)由菱形的性质得出OA=OC,BD⊥AC,BO=BD=1,利用勾股定理求出OA=2,从而得AC =2OA =4,根据直角三角形斜边中线的性质可得OE=AC=2.
24.(1)解:过点B作交直线于点D,如图,
∴∠BDC=90°,
∴∠DBC+∠BCD=90°,
∵∠AOC=90°,
∴∠BDC=∠AOC,
∵∠ACB=90°,
∴∠BCD+∠ACO=90°,
∴∠ACO=∠DBC,
在和中,
,
∴,
∴,
∵点A坐标为,C的坐标为,
∴,
∴,
∴点B的坐标为,
故答案为:;
(2)解:过点B作轴交y轴于点E,如图,
∵∠AOC=∠ACB=90°,
∴,
∴,,
∴,
在和中,
,
∵,
∴,
∵点C的坐标为,A点的坐标为,
∴,
∴
∴,
∴点B的坐标;
(3)解:过点B作轴交x轴于点E,如图,
则,
∵点在y轴正半轴上运动,点在第四象限,
∴,,
同理可证,,
∴,
∵,
∴,
∴.
(1)过点B作交直线于点D,利用“一线三垂直”全等三角形模型可证明,从而得,结合点A、C的坐标得,根据即可求得点B坐标;
(2)过点B作轴交y轴于点E,同理利用“一线三垂直”全等三角形模型可证明,结合点A、C的坐标得根据即可求得点B坐标;
(3)过点B作轴交x轴于点E,则,根据点坐标得,,同理可证,,则,结合即可求得关系式.
(1)解:过点B作交直线于点D,如图,
∵,,,
∴,
∴,
∵点A坐标为,C的坐标为,
∴,
∴,
则点B的坐标为,
故答案为:;
(2)解:过点B作交于点E,如图,
∵点C的坐标为,A点的坐标为,
∴,
∵,
∴,,
∴,
∵,
∴,
∴
则,
那么,点B的坐标;
(3)解:过点B作交于点E,如图,
则,
∵点在y轴正半轴上运动,点在第四象限,
∴,,
同理可证,,
∴,
∵,
∴,
则.
25.(1)(3,0);(0,4)
(2)解:设过点、的直线解析式为,
则有:
,
解得:,
故直线的表达式
(3)解:由(1)可知,
,,
当时,此时D与B重合,
D点坐标为,
当时,如图,D点在的垂直平分线上,
此时D点的横坐标为:,
将代入,
求得,
D点坐标为,
故D点坐标为或.
解:(1)直线与x轴、y轴分别交于A、B两点,
令即,解得,
令得,
即点A坐标为,点B坐标为,
故答案为:(3,0),(0,4).
(1)分别令x=0、y=0,求出y、x的值,可得点A、B的坐标;
(2)设直线BC的解析式为y=kx+b,将点B、C的坐标代入求出k、b的值,据此可得直线BC的解析式;
(3)易得AC、AB的值,当AD=AC时,此时D与B重合,据此可得点D的坐标;当AD=CD时,D点在AC的垂直平分线上,求出点D的横坐标,然后代入y=2x+4中求出y的值,据此可得点D的坐标.
20224-2025学年八年级上册期末押题卷(北师大版)
数学
考试范围:八上全册 考试时间:100分钟
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
一、单选题
1.定西剪纸是一种甘肃省的传统民间剪纸艺术,作为一种镂空艺术,它能给人以视觉上透空的感觉和艺术享受.下列作品中,是轴对称图形的是( )
A. B.
C. D.
2.下列运算正确的是( )
A. B.
C. D.
3.如图,AB=AD,点B关于AC的对称点E恰好落在CD上.若∠BAD=α(0°<a<180°),∠ACB=β,则下列关系正确的是( )
A.a﹣β=90° B.α+β=180°
C.c=3β D.a+2β=180°
4.下列命题的逆命题是假命题的是( )
A.等腰三角形的两个底角相等 B.全等三角形的对应边都相等
C.两直线平行,同旁内角互补 D.对顶角相等
5.关于的一元二次方程有实数根,则满足( )
A. B.且 C.且 D.
6.若,则的值为( )
A. B. C. D.
7.已知正比例函数,下列结论正确的是( )
A.图象经过第一、三象限 B.图象是一条射线
C.不论取何值,总有 D.随的增大而减小
8.如图中,,若将作点逆时针旋转,得到,连接,则在点运动过程中,线段的最小值为( )
A.2 B. C. D.1
9.如图,在平面直角坐标系中,菱形的顶点A在y轴的正半轴上,顶点B、C在x轴的正半轴上,,.点M在菱形的边和上运动(不与点A,C重合),过点M作轴,与菱形的另一边交于点N,连接,,设点M的横坐标为x,的面积为y,则下列图象能正确反映y与x之间函数关系的是( )
A. B.
C. D.
10.如图,在中,,,,是边上的高.点E,F分别在边,上(不与端点重合),且.设,四边形的面积为y,则y关于x的函数图象为( )
A. B.
C. D.
二、填空题
11.若函数是正比例函数,则的值是 .
12.如图,在矩形中,E为上一点,将矩形的一角沿向上折叠,点B的对应点F恰好落在边上.若的周长为12,的周长为24,则的长为 .
13.若,则的值是 .
14.如图,在△ABC中,CP平分∠ACB,AP⊥CP于点P,已知△ABC的面积为12cm2,则阴影部分的面积为 cm2.
15.若关于x的不等式组的解集为,关于y的分式方程有非负整数解,则符合条件的所有整数a的和为 .
16.如图,在等腰中,,,点是边上一动点,将线段绕点顺时针旋转,得到线段,连接, ,则的最小值是 .
三、解答题
17.计算:
(1);
.
18.解方程:
(1);
.
解不等式组,并把解集在数轴上表示出来.
20.如图,等边三角形中,D、E分别为边上的两动点,与交于点F,于点G,若,求的大小.
21.2023年10月,成都某景区就开始为冬季旅游做宣传,致使游客人数逐月增加. 10月份游客人数为万人,12月份游客人数为万人.若平均每月增长的百分率相同,请解答下列问题:
(1)求这两个月该景区游客人数的月平均增长率;
(2)预计今年1月份该景区游客人数会继续增长,已知该景区1月1日至1月4日已接待游客万人,则在1月份剩余天数中,该景区至少还需接待游客多少万人才能保证月平均增长率不降低?
22.如图,在中,,点D是边的中点,点O在边上,经过点C且与边相切于点E,.
(1)求证:是的切线;
(2)若,求的半径长.
23.如图,在四边形ABCD中,AB//DC,AB=AD,对角线AC,BD交于点O,AC平分∠BAD,过点C作CE⊥AB交AB的延长线于点E,连接OE。
(1)求证:四边形ABCD是菱形;
(2)若AB= ,BD=2,求OE的长.
24.如图1,等腰直角三角形中,,直线经过点C,过点A作于点D,过点B作于点E,可以证明,我们将这个模型称为“一线三直角”.接下来我们就利用这个模型来解决一些问题:
(1)如图2,将一块等腰直角三角板放置在平面直角坐标系中,,点A在y轴的正半轴上,点C在x轴的负半轴上,点B在第二象限,点A坐标为,C的坐标为,则点B的坐标为_______;
(2)如图3,在平面直角坐标系中,等腰,与y轴交点D,点C的坐标为,A点的坐标为,求点B的坐标.
(3)如图4,等腰,,当点C在x轴正半轴上运动,点在y轴正半轴上运动,点在第四象限时,作轴于点D,请直接写出a,m,n之间的关系.
25.如图,在平面直角坐标系中,直线与x轴、y轴分别交于A、B两点,过点B的直线交x轴与点
(1)点A坐标为 ,点B坐标为 ;
(2)求直线的表达式;
(3)若点D在直线上,且是以为腰的等腰三角形,点D的坐标.
答案解析部分
1.B
解:A、∵该图形不是轴对称,∴A不符合题意;
B、∵该图形是轴对称,∴B符合题意;
C、∵该图形不是轴对称,∴C不符合题意;
D、∵该图形不是轴对称,∴D不符合题意;
故答案为:B.
利用轴对称图形的定义(如果一个图形沿着一条直线对折后两部分完全重合,这样的图形叫做轴对称图形,这条直线叫做对称轴)逐项分析判断即可.
2.B
解:A、 ,故此项不符合题意;
B、 ,故此项符合题意;
C、与不是同类二次根式,不能合并,故此项不符合题意;
D、 ,故此项不符合题意;
故答案为:B.
根据二次根式的性质、积的乘方、二次根式的加减、有理数的加法分别计算,再判断即可.
3.D
解:∵点B关于AC的对称点E恰好落在CD上,
∴AB=AE,∠ACE=∠ACB,∠BAC=∠EAC,
∵AB=AD,
∴∠D=∠AED,
又∠AED=∠ACE+∠EAC,
∠DAE+∠D+∠AED=180°,
∴∠DAE+∠ACE+∠EAC+∠ACE+∠EAC=180°,
∴∠DAE+β+∠EAC+β+∠EAC=180°,
∴ α+2β=180°,
故答案为:D.
先利用“在同一个三角形,等边对等角”,证明∠D=∠AED,再利用三角形外角的性质,得出∠AED=∠ACE+∠EAC,再根据三角形内角和定理,得到∠DAE+∠D+∠AED=180°,转化为 α , β 表示的式子即可.
4.D
解:A、等腰三角形的两个底角相等的逆命题:两个角相等的三角形是等腰三角形,是真命题,故不符合题意;
B、全等三角形的对应边都相等的逆命题:三边对应相等的两个三角形全等,是真命题,故不符合题意;
C、两直线平行,同旁内角互补的逆命题:同旁内角互补,两直线平行,是真命题,故不符合题意;
D、对顶角相等的逆命题:如果两个角相等,那么这两个角是对顶角,是假命题,故符合题意.
故答案为:D.
一个命题包括题设与结论两部分,将一个命题的题设与结论互换位置即可得出原命题的逆命题,据此先写出各项命题的逆命题,再根据等腰三角形的判定、全等三角形的判定,平行线的判定、对顶角的性质分别判断即可.
5.C
解:∵ 一元二次方程有实数根,
∴,
解得:
故C正确,A、B、D错误,
故答案为:C.
由一元二次方程有实数根,故可知根的判别式大于或者等于零,且要注意a的取值不能使二次项系数为零,综合可知a的取值范围。
6.A
∵,
∴2a-4=0,b+1=0,
∴a=2,b=-1,
∴ab=2×(-1)=-2,
故答案为:A.
先利用非负数之和为0的性质求出a、b的值,再将a、b的值代入ab计算即可.
7.D
解:A、,图象在第二、四象限,A不符合题意;
B、正比例函数的图象是一条直线,B不符合题意;
C、应为当时,,C不符合题意;
D、,随的增大而减小,D不符合题意;
故答案为:D
根据一次函数的图象与系数的关系结合一次函数的性质即可求解。
8.A
如图,在上截取,连接,
将绕点逆时针旋转得到,
,
,即,
在和中,
,
,
,
点在线段上运动,
当时,的值最小,即线段有最小值,
是等腰直角三角形,
,
,
是等腰直角三角形,
,,
,
由勾股定理得,
线段有最小值为2,
故答案为:A.
根据题意先求出,再利用全等三角形的判定与性质证明求解即可。
9.A
10.A
解:过点D作DM⊥AB于点M,作DN⊥BC于点N,如下图:
∵,,,
∴,
∵是边上的高.
∴,
∴,
∵,,
∴,
∴,
解得:,
∴
∵DM⊥AB,∠ABC=90°,
∴DM//AB,
∴△ADM∽△ACB,
∴,即,
∴
∵DN//AB,
∴△CDN∽△CAB,
∴,即,
∴.
∵,,
∴,,
∴,
∴.
∵AE=x,
∴BF=0.5x.
∴
∵,
∴当时, ,
当时,.
故答案为:A.
过点D作DM⊥AB于点M,作DN⊥BC于点N,由勾股定理求出,根据等面积法求出,DM和DN的长,证明,由相似三角形的性质可求出的长,继而可得DC的长;再证明 △ADM∽△ACB和△CDN∽△CAB,分别由相似三角形的性质可得出求出DM和DN的长,证明,可得AE:BF=2,据此表示出BF的长,利用,表示出两个三角形的面积,代入数据可得关于x的一次函数的解析式,最后根据自变量的大小求出对应的函数值.
11.3
解:根据题意,得:m-2=1,
∴m=3.
故第一空答案为:3.
根据正比例函数的定义,直接列出方程m-2=1,解方程求出m的值即可。
12.4
解:四边形是矩形,
,,∠D=90°,
∵将矩形的一角沿向上折叠,点B的对应点F恰好落在边上,
∴,,
的周长为12,的周长为24,
,,
,
,
,,
在中,由勾股定理得,
,
∴,
,
,
故答案为:4.
由矩形和折叠的性质可知,,,,∠D=90°,再根据三角形周长,求得,,然后在中,利用勾股定理得的长,即可求出AF=AD-DF的长.
13.6
14.6
解:延长AP交BC于Q,
∵ CP平分∠ACB
∴∠ACP=∠PCQ,
∵ AP⊥CP于点P,
∴∠APC=∠QPC,
又PC=PC,
∴△APC≌△QPC(AAS),
∴AP=PQ,
∴S△ABP=S△ABQ,S△APC=S△AQC,
∴S阴影部分=S△ABP+S△APC=(S△ABQ+S△AQC)=S△ABC=6( cm2).
故答案为:6.
先利用AAS证明△APC≌△QPC,再利用全等三角形的性质,证明AP=PQ,然后利用S阴影部分=S△ABP+S△APC求解.
15.
16.
17.(1)解:原式
;
(2)解:原式
.
(1)利用二次根式的乘除法的计算方法及步骤(①先将除法转换为乘法;②再利用二次根式的乘法的计算方法计算)分析求解即可;
(2)先利用平方差公式和完全平方公式展开,再计算即可.
(1)解:原式
;
(2)解:原式
.
18.(1)
(2)
19.解:,
解不等式①得:,
解不等式②得:,
∴不等式组的解集为,
在数轴上表示为:
由题意先求出每一个不等式的解集,再找出各解集的公共部分即为不等式组的解集;在数轴上表示解集时,再根据“>”空心向右、“≤”实心向左即可求解.
20.解:∵等边三角形,
∴,,
∵,,,
∴,
∴,
∴,
∴,
∴,
∴的大小为.
本题考查等边三角形的性质,全等三角形的判定与性质,三角形外角的性质,三角形内角和定理.利用等边三角形的性质可得,,再结合,,,利用全等三角形的判定定理可证明,利用全等三角形的性质可得:,,,根据,代入数据可求出的大小.
21.(1)
(2)
22.(1)证明:如图,作,垂足为点H,连接,
∵,D是的中点,
∴,
∴,
∵,
又∵,
∴,
即是的平分线,
∵点O在上,与相切于点E,
∴,且是的半径,
∴,是的半径,
∴是的切线;
(2)解:在中,,
∴,
∵是的切线,
∴,
∴,
设的半径为r,则,
在中,由勾股定理得:,
∴,
∴.
∴的半径长为3.
(1)作,垂足为点H,连接,先证出,且是的半径,再结合,是的半径,即可证出是的切线;
(2)设的半径为r,则,利用勾股定理可得,再求出r的值即可.
(1)证明:如图,作,垂足为点H,连接,
∵,D是的中点,
∴,
∴,
∵,
又∵,
∴,
即是的平分线,
∵点O在上,与相切于点E,
∴,且是的半径,
∴,是的半径,
∴是的切线;
(2)解:在中,,
∴,
∵是的切线,
∴,
∴,
设的半径为r,则,
在中,由勾股定理得:,
∴,
∴.
∴的半径长为3.
23.(1)∵AB∥CD,∴∠OAB=∠DCA,
∵AC平分∠BAD,∴∠OAB=∠DAC,
∴CD=AD=AB,
∵AB∥CD,
∴四边形ABCD是平行四边形,
∵AD=AB,
∴平行四边形ABCD是菱形;
(2)解: ∵四边形ABCD是菱形,
∴OA=OC,BD⊥AC,BO=BD=1,
∴OA==2,
∴AC =2OA =4,
∵CE⊥AB,∴∠AEC=90°,
∴OE=AC=2.
(1)由平行线的性质得出∠OAB=∠DCA,由角平分线的定义得出∠OAB=∠DAC,利用等角对等边可得CD=AD=AB,结合AB∥CD,即证四边形ABCD是菱形;
(2)由菱形的性质得出OA=OC,BD⊥AC,BO=BD=1,利用勾股定理求出OA=2,从而得AC =2OA =4,根据直角三角形斜边中线的性质可得OE=AC=2.
24.(1)解:过点B作交直线于点D,如图,
∴∠BDC=90°,
∴∠DBC+∠BCD=90°,
∵∠AOC=90°,
∴∠BDC=∠AOC,
∵∠ACB=90°,
∴∠BCD+∠ACO=90°,
∴∠ACO=∠DBC,
在和中,
,
∴,
∴,
∵点A坐标为,C的坐标为,
∴,
∴,
∴点B的坐标为,
故答案为:;
(2)解:过点B作轴交y轴于点E,如图,
∵∠AOC=∠ACB=90°,
∴,
∴,,
∴,
在和中,
,
∵,
∴,
∵点C的坐标为,A点的坐标为,
∴,
∴
∴,
∴点B的坐标;
(3)解:过点B作轴交x轴于点E,如图,
则,
∵点在y轴正半轴上运动,点在第四象限,
∴,,
同理可证,,
∴,
∵,
∴,
∴.
(1)过点B作交直线于点D,利用“一线三垂直”全等三角形模型可证明,从而得,结合点A、C的坐标得,根据即可求得点B坐标;
(2)过点B作轴交y轴于点E,同理利用“一线三垂直”全等三角形模型可证明,结合点A、C的坐标得根据即可求得点B坐标;
(3)过点B作轴交x轴于点E,则,根据点坐标得,,同理可证,,则,结合即可求得关系式.
(1)解:过点B作交直线于点D,如图,
∵,,,
∴,
∴,
∵点A坐标为,C的坐标为,
∴,
∴,
则点B的坐标为,
故答案为:;
(2)解:过点B作交于点E,如图,
∵点C的坐标为,A点的坐标为,
∴,
∵,
∴,,
∴,
∵,
∴,
∴
则,
那么,点B的坐标;
(3)解:过点B作交于点E,如图,
则,
∵点在y轴正半轴上运动,点在第四象限,
∴,,
同理可证,,
∴,
∵,
∴,
则.
25.(1)(3,0);(0,4)
(2)解:设过点、的直线解析式为,
则有:
,
解得:,
故直线的表达式
(3)解:由(1)可知,
,,
当时,此时D与B重合,
D点坐标为,
当时,如图,D点在的垂直平分线上,
此时D点的横坐标为:,
将代入,
求得,
D点坐标为,
故D点坐标为或.
解:(1)直线与x轴、y轴分别交于A、B两点,
令即,解得,
令得,
即点A坐标为,点B坐标为,
故答案为:(3,0),(0,4).
(1)分别令x=0、y=0,求出y、x的值,可得点A、B的坐标;
(2)设直线BC的解析式为y=kx+b,将点B、C的坐标代入求出k、b的值,据此可得直线BC的解析式;
(3)易得AC、AB的值,当AD=AC时,此时D与B重合,据此可得点D的坐标;当AD=CD时,D点在AC的垂直平分线上,求出点D的横坐标,然后代入y=2x+4中求出y的值,据此可得点D的坐标.
同课章节目录
