湖南省长沙市双城第二中学2024-2025学年高一上学期期末数学试卷(PDF版,含答案)
文档属性
| 名称 | 湖南省长沙市双城第二中学2024-2025学年高一上学期期末数学试卷(PDF版,含答案) |

|
|
| 格式 | |||
| 文件大小 | 573.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-09 00:00:00 | ||
图片预览



文档简介
湖南省长沙市双城第二中学 2024-2025 学年高一上学期期末数学试卷
一、单选题:本题共 8 小题,每小题 5 分,共 40 分。在每小题给出的选项中,只有一项是符合题目要求的。
1 + | | , ≤ 1
1.已知函数 ( ) = { ,方程 ( ) 1 = 0有两解,则 的取值范围是( )
( + 1)2 +2 , > 1
1 1
A. ( , 1) B. (0, ) C. (0,1) D. (1,+∞)
2 2
2.已知函数 ( ) = 2 3,则不等式 (3 2) > (2 5)的解集为( )
A. ( 4,2) B. ( ∞,2)
C. ( ∞, 2) ∪ (2,+∞) D. ( ∞, 4) ∪ (2,+∞)
3.已知函数 ( ) = + ,其中 ∈ , ∈ ,如果对任意 ∈ ,都有 ( ) ≠ 2,那么在下列不等
式中一定成立的是( )
A. 4 < + < 4 B. 4 < < 4 C. 2 + 2 < 2 D. 2 + 2 < 4
4.已知角 的顶点在坐标原点,始边与 轴的非负半轴重合,终边经过点 ( , √ )( > 0),则( )
A. 2 > 0 B. 2 < 0 C. 2 > 0 D. 2 < 0
5.下列函数是奇函数且在区间(0,1)上是增函数的是( )
1
A. = B. = 3 C. = 2 D. =
6.已知集合 = { 1,1,2,3,4,5}, = { ∈ |( 1)( 5) < 0},则 =( )
A. {3} B. {2,3} C. {2,3,5} D. { 1,1,5}
1
7.已知锐角 满足√ 3sin cos = 1.若要得到函数 ( ) = 2( + )的图象,则可以将函数 =
2
1
sin2 的图象( ).
2
7
A. 向左平移 个单位长度 B. 向左平移 个单位长度
12 12
7
C. 向右平移 个单位长度 D. 向右平移 个单位长度
12 12
8.“ < 1”是“ 2 4 + 3 > 0”的( )
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
二、多选题:本题共 4 小题,共 24 分。在每小题给出的选项中,有多项符合题目要求。
1
9.已知 ( )是定义在 上不恒为0的函数, ( 1)的图象关于直线 = 1对称,且函数 = 的图象的对称
2
中心也是 ( )图象的一个对称中心,则( )
第 1 页,共 9 页
A. 点( 2,0)是 ( )的图象的一个对称中心
B. ( )为周期函数,且4是 ( )的一个周期
C. (4 )为偶函数
D. (31) + (35) = 2
10.已知定义在 上的函数 ( )满足:对 , ∈ , ( + ) + ( ) = 2 ( ) ( ),且 (0) = 1, ( ) =
2
1,则以下结论正确的为( )
A. ( ) = 0 B. ( ) = 0 C. ( ) = ( ) D. ( + ) = ( )
4
11.已知函数 ( ) = √ 3cos2 sin cos ,则( )
2 2 2
A. 函数 ( )的最小正周期为4
2 √ 3
B. 点( , )是函数 ( )图象的一个对称中心
3 2
5
C. 将函数 ( )图象向左平移 个单位长度,所得到的函数图象关于 轴对称
6
D. 函数 ( )在区间( , 0)上单调递减
6
12.下列说法正确的是( )
1 1
A. “ > ”是“ < ”的充分不必要条件
B. ∩ = 是 = 的必要不充分条件
C. 若 , , ∈ ,则“ 2 > 2”的充要条件是“ > ”
D. 若 , ∈ ,则“ 2 + 2 ≠ 0”是“| | + | | ≠ 0”的充要条件
三、填空题:本题共 3 小题,每小题 5 分,共 15 分。
13.已知 √ 2 = √ 3,则 =______.
3
14.角 的终边经过点 (4, ),且 = ,则 =______.
5
15.已知 ( )是定义在 ,且满足 ( + 2) = ( 2),当 ∈ [0,4)时, ( ) = | 2 4 + 3|,若函数 =
( ) 在区间[ 4,6]上有10个不同零点,则实数 的取值范围是 .
四、解答题:本题共 6 小题,共 72 分。解答应写出文字说明,证明过程或演算步骤。
16.(本小题12分)
已知函数 ( ) = 2
5( + 2 + 1)的定义域为 , ( ) = .
2+1
4
第 2 页,共 9 页
3
(1)若 = ,求函数 ( )的值域;
4
(2)若 = ( , ),且[ ( ) ( )]2 ≤ 10,求实数 的取值范围.
17.(本小题12分)
5
∫如图为函数 ( ) = 2 ( + )( > 0, | | < )的部分图象,且| | = , ( , 2).
2 4 12
(1)求 , 的值;
3
(2)将 ( )的图象上所有点的横坐标扩大到原来的3倍(纵坐标不变),再向右平移 个单位长度,得到函数
4
( )的图象,讨论函数 = ( ) 在区间[ , ]的零点个数.
2
18.(本小题12分)
已知函数 ( ) = 2 (√ 3 ) + 1, ∈ .
(1)求曲线 : = ( )的对称中心;
(2)在锐角三角形 中, , , 分别是内角 、 、 的对边,且 ( ) = 2.若 + ≤ 恒成立,求实数 的
2
最小值.
19.(本小题12分)
请解答以下问题,要求解决两个问题的方法不同.
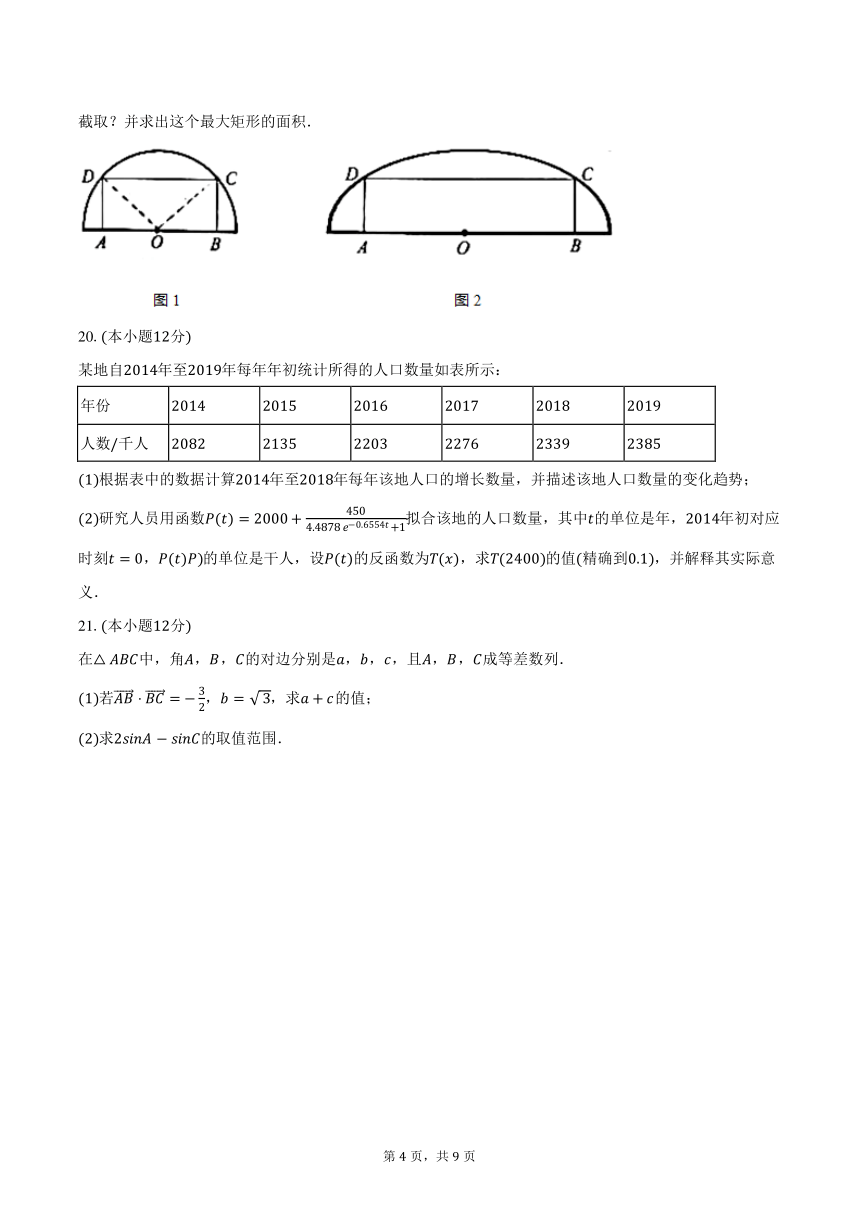
(1)如图1,要在一个半径为1米的半圆形铁板中截取一块面积最大的矩形 ,如何截取?并求出这个最
大矩形的面积.
(2)如图2,要在一个长半轴为2米,短半轴为1米的半个椭圆形铁板中截取一块面积最大的矩形 ,如何
第 3 页,共 9 页
截取?并求出这个最大矩形的面积.
20.(本小题12分)
某地自2014年至2019年每年年初统计所得的人口数量如表所示:
年份 2014 2015 2016 2017 2018 2019
人数/千人 2082 2135 2203 2276 2339 2385
(1)根据表中的数据计算2014年至2018年每年该地人口的增长数量,并描述该地人口数量的变化趋势;
450
(2)研究人员用函数 ( ) = 2000+ 0.6554 拟合该地的人口数量,其中 的单位是年,2014年初对应4.4878 +1
时刻 = 0, ( ) )的单位是干人,设 ( )的反函数为 ( ),求 (2400)的值(精确到0.1),并解释其实际意
义.
21.(本小题12分)
在△ 中,角 , , 的对边分别是 , , ,且 , , 成等差数列.
3
(1)若 = , = √ 3,求 + 的值;
2
(2)求2 的取值范围.
第 4 页,共 9 页
1.【答案】
2.【答案】
3.【答案】
4.【答案】
5.【答案】
6.【答案】
7.【答案】
8.【答案】
9.【答案】
10.【答案】
11.【答案】
12.【答案】
√ 2
13.【答案】
2
3
14.【答案】
4
15.【答案】(0,1)
3 3
16.【答案】解:(1)当 = 时, ( ) = 5( 2 + +1),
4 2
4
3 1 1
由 2 + + 1 = ( + 2)( + ) > 0,解得 < < 2,
2 2 2
1
即函数 ( )的定义域为( , 2),
2
3 25
令 = 2 + + 1,则 ∈ (0, ],
2 16
从而 ( )的值域为( ∞,2].
(2)由于 = ( , ),且 = 4 2 + 4 > 0,
所以方程 2 + 2 + 1 = 0的两根分别为 , ,且 + = 2 , = 1,
又[ ( ) ( )]2 ≤ 10,即( 2
2
+1 2
) ≤ 10,
+1
将 + = 2 , = 1代入整理得:
1 1 2
3
2 +
3 2 + 3 + 2 1 ( ) 1( ) = × [ ] = × [ ]2 = ( )2 ≤ 10,
4 2+1 2+1 4 ( 2+1)( 2+1) 4 2( ) 4
从而( + )2 4 ≤ 40,
第 5 页,共 9 页
所以 2 9 ≤ 0,解得 3 ≤ ≤ 3,
即实数 的取值范围为[ 3,3].
2
17.【答案】解:(1)根据题意得, = ,故 = , = = 2,故 ( ) = 2 (2 + ).
4 4
5 5
将 ( , 2)代入,得2 × ( ) + = + 2 ( ∈ ),解得 = +2 ( ∈ )
12 12 6
,
又| | < ,故 = 2 6.
(2) 2 3 2 2 依题意, ( ) = 2 [ ( ) ] = 2 ( ).
3 4 6 3 3
函数 = ( ) 在区间[ , ]的零点个数即为函数 ( )的图象与直线 = 在[ , ]2 2 上的交点个数.
2 2 4
当 ∈ [ , ]2 时, ∈ [ , ],结合余弦函数图象可知, 3 3 3 3
当 ∈ [ , ]时, ( )单调递减,当 ∈ ( , ]时, ( )2 2 2 单调递增,
且 ( ) = 1, ( ) = 1, ( ) = 22 2 ,
作出函数 ( )在[ , ]2 上的大致图象如图所示.
观察可知,当 = 2或 1 < ≤ 1时, = ( ) 有1个零点;
当 2 < ≤ 1时, = ( ) 有2个零点;
当 < 2或 > 1时, = ( ) 有0个零点.
18.【答案】解:(1)由题意,得 ( ) = 2√ 3 2 2 + 1 = √ 3 2 + 2 = 2 (2 + ).
6
令2 + = , ∈ ,得 = + , ∈ ,
6 12 2
∴曲线 = ( )的对称中心为( + , 0), ∈ .
12 2
(2) ( ) = 2 ( + ) = 2,即sin( + ) = 1.
2 6 6
∵ 是锐角三角形 的内角,
∴ + = ,
6 2
第 6 页,共 9 页
∴ = .
3
+ + 2√ 3 2√ 3 2√ 3 3 √ 3
由正弦定理得 = = ( + ) = [sin( + )+ ] = × ( + ) =
3 3 3 2 2
2 ( + ).
6
0 < <
在锐角三角形 中,{ 22 ,
0 < <
3 2
解得 ∈ ( , ),
6 2
2
∴ + ∈ ( , ),
6 3 3
√ 3
∴ sin( + ) ∈ ( , 1].
6 2
+
即√ 3 < ≤ 2,
∴ ≥ 2,即实数 的最小值为2.
19.【答案】解:(1)设∠ = ,(0 < < );
2
∴ = , = ;
∵ = 2 ,
∴ ═2 = 2 ;
√ 2
∴当 = 时,即 = 时,矩形面积最大为1;
4 2
2
(2)依题意可得:椭圆方程为: + 2 = 1, ( ≥ 0);
4
设:点 坐标为( , )即: = , = ;
∴ = 2 = 2 ;
∵点 为椭圆上的点;
2
∴ + 2 = 1;
4
2 2
∵ + 2 ≥ 2√
2 = ;
4 4
1
∴ ≤ 1,当且仅当 = = 时取等号;
2 2
∴ ≤ 2;
即矩形面积最大为2;当 = √ 2时取等号;
第 7 页,共 9 页
20.【答案】解:(1)2014年至2019年每年该地人口的增长数量为2385 2082 = 303千人,
3135 2082 = 53,2203 2135 = 68,2276 2203= 73,2339 2276 = 63,2385 2339 = 46,
由上述数据可得从2014年到2019年每年人口增长数量呈先增加后减少的变化趋势,每一年人口总数呈逐渐
递增的变化趋势,
450
(2)由 ( ) = 2000+
4.4878 0.6554
,
+1
∵ ( )的反函数为 ( ),
450
∴ 2400 = 2000+
4.4878 0.6654
,
+1
∴ 4.4878 0.6554
450
+1 = ,
400
∴ 4.4878 0.6554
1
= ,
8
两边取对数可得 4.4878 0.6554 = 8,
4.4878+ 8 35.9024
∴ = = ≈ 5.5,
0.6554 0.6554
∴ (2400) = 5.5.
其实际意义为:可根据数学模型预测人口数量增长规律,及提供有效数据,即经过半年时间,该地人口数
量人数即增长到2400千人.
21.【答案】解:(1) ∵ , , 成等差数列,
∴ = ,
3
∵
3
· = ,
2
3
∴ ( ) = ,
2
1 3 1
∴ = , ,即 = 3.
2 2 2
∵ = √ 3, 2 = 2 + 2 2 ,
∴ 2 + 2 = 3,即( + )2 3 = 3,
∴ ( + )2 = 12,所以 + = 2√ 3;
2 √ 3 1
(2)2 = 2 ( ) = 2( + ) = √ 3 ,
3 2 2
2
∵ 0 < < ,
3
第 8 页,共 9 页
√ 3
∴ √ 3 ∈ ( ,√ 3),
2
√ 3
∴ 2 的取值范围是( , √ 3).
2
第 9 页,共 9 页
一、单选题:本题共 8 小题,每小题 5 分,共 40 分。在每小题给出的选项中,只有一项是符合题目要求的。
1 + | | , ≤ 1
1.已知函数 ( ) = { ,方程 ( ) 1 = 0有两解,则 的取值范围是( )
( + 1)2 +2 , > 1
1 1
A. ( , 1) B. (0, ) C. (0,1) D. (1,+∞)
2 2
2.已知函数 ( ) = 2 3,则不等式 (3 2) > (2 5)的解集为( )
A. ( 4,2) B. ( ∞,2)
C. ( ∞, 2) ∪ (2,+∞) D. ( ∞, 4) ∪ (2,+∞)
3.已知函数 ( ) = + ,其中 ∈ , ∈ ,如果对任意 ∈ ,都有 ( ) ≠ 2,那么在下列不等
式中一定成立的是( )
A. 4 < + < 4 B. 4 < < 4 C. 2 + 2 < 2 D. 2 + 2 < 4
4.已知角 的顶点在坐标原点,始边与 轴的非负半轴重合,终边经过点 ( , √ )( > 0),则( )
A. 2 > 0 B. 2 < 0 C. 2 > 0 D. 2 < 0
5.下列函数是奇函数且在区间(0,1)上是增函数的是( )
1
A. = B. = 3 C. = 2 D. =
6.已知集合 = { 1,1,2,3,4,5}, = { ∈ |( 1)( 5) < 0},则 =( )
A. {3} B. {2,3} C. {2,3,5} D. { 1,1,5}
1
7.已知锐角 满足√ 3sin cos = 1.若要得到函数 ( ) = 2( + )的图象,则可以将函数 =
2
1
sin2 的图象( ).
2
7
A. 向左平移 个单位长度 B. 向左平移 个单位长度
12 12
7
C. 向右平移 个单位长度 D. 向右平移 个单位长度
12 12
8.“ < 1”是“ 2 4 + 3 > 0”的( )
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
二、多选题:本题共 4 小题,共 24 分。在每小题给出的选项中,有多项符合题目要求。
1
9.已知 ( )是定义在 上不恒为0的函数, ( 1)的图象关于直线 = 1对称,且函数 = 的图象的对称
2
中心也是 ( )图象的一个对称中心,则( )
第 1 页,共 9 页
A. 点( 2,0)是 ( )的图象的一个对称中心
B. ( )为周期函数,且4是 ( )的一个周期
C. (4 )为偶函数
D. (31) + (35) = 2
10.已知定义在 上的函数 ( )满足:对 , ∈ , ( + ) + ( ) = 2 ( ) ( ),且 (0) = 1, ( ) =
2
1,则以下结论正确的为( )
A. ( ) = 0 B. ( ) = 0 C. ( ) = ( ) D. ( + ) = ( )
4
11.已知函数 ( ) = √ 3cos2 sin cos ,则( )
2 2 2
A. 函数 ( )的最小正周期为4
2 √ 3
B. 点( , )是函数 ( )图象的一个对称中心
3 2
5
C. 将函数 ( )图象向左平移 个单位长度,所得到的函数图象关于 轴对称
6
D. 函数 ( )在区间( , 0)上单调递减
6
12.下列说法正确的是( )
1 1
A. “ > ”是“ < ”的充分不必要条件
B. ∩ = 是 = 的必要不充分条件
C. 若 , , ∈ ,则“ 2 > 2”的充要条件是“ > ”
D. 若 , ∈ ,则“ 2 + 2 ≠ 0”是“| | + | | ≠ 0”的充要条件
三、填空题:本题共 3 小题,每小题 5 分,共 15 分。
13.已知 √ 2 = √ 3,则 =______.
3
14.角 的终边经过点 (4, ),且 = ,则 =______.
5
15.已知 ( )是定义在 ,且满足 ( + 2) = ( 2),当 ∈ [0,4)时, ( ) = | 2 4 + 3|,若函数 =
( ) 在区间[ 4,6]上有10个不同零点,则实数 的取值范围是 .
四、解答题:本题共 6 小题,共 72 分。解答应写出文字说明,证明过程或演算步骤。
16.(本小题12分)
已知函数 ( ) = 2
5( + 2 + 1)的定义域为 , ( ) = .
2+1
4
第 2 页,共 9 页
3
(1)若 = ,求函数 ( )的值域;
4
(2)若 = ( , ),且[ ( ) ( )]2 ≤ 10,求实数 的取值范围.
17.(本小题12分)
5
∫如图为函数 ( ) = 2 ( + )( > 0, | | < )的部分图象,且| | = , ( , 2).
2 4 12
(1)求 , 的值;
3
(2)将 ( )的图象上所有点的横坐标扩大到原来的3倍(纵坐标不变),再向右平移 个单位长度,得到函数
4
( )的图象,讨论函数 = ( ) 在区间[ , ]的零点个数.
2
18.(本小题12分)
已知函数 ( ) = 2 (√ 3 ) + 1, ∈ .
(1)求曲线 : = ( )的对称中心;
(2)在锐角三角形 中, , , 分别是内角 、 、 的对边,且 ( ) = 2.若 + ≤ 恒成立,求实数 的
2
最小值.
19.(本小题12分)
请解答以下问题,要求解决两个问题的方法不同.
(1)如图1,要在一个半径为1米的半圆形铁板中截取一块面积最大的矩形 ,如何截取?并求出这个最
大矩形的面积.
(2)如图2,要在一个长半轴为2米,短半轴为1米的半个椭圆形铁板中截取一块面积最大的矩形 ,如何
第 3 页,共 9 页
截取?并求出这个最大矩形的面积.
20.(本小题12分)
某地自2014年至2019年每年年初统计所得的人口数量如表所示:
年份 2014 2015 2016 2017 2018 2019
人数/千人 2082 2135 2203 2276 2339 2385
(1)根据表中的数据计算2014年至2018年每年该地人口的增长数量,并描述该地人口数量的变化趋势;
450
(2)研究人员用函数 ( ) = 2000+ 0.6554 拟合该地的人口数量,其中 的单位是年,2014年初对应4.4878 +1
时刻 = 0, ( ) )的单位是干人,设 ( )的反函数为 ( ),求 (2400)的值(精确到0.1),并解释其实际意
义.
21.(本小题12分)
在△ 中,角 , , 的对边分别是 , , ,且 , , 成等差数列.
3
(1)若 = , = √ 3,求 + 的值;
2
(2)求2 的取值范围.
第 4 页,共 9 页
1.【答案】
2.【答案】
3.【答案】
4.【答案】
5.【答案】
6.【答案】
7.【答案】
8.【答案】
9.【答案】
10.【答案】
11.【答案】
12.【答案】
√ 2
13.【答案】
2
3
14.【答案】
4
15.【答案】(0,1)
3 3
16.【答案】解:(1)当 = 时, ( ) = 5( 2 + +1),
4 2
4
3 1 1
由 2 + + 1 = ( + 2)( + ) > 0,解得 < < 2,
2 2 2
1
即函数 ( )的定义域为( , 2),
2
3 25
令 = 2 + + 1,则 ∈ (0, ],
2 16
从而 ( )的值域为( ∞,2].
(2)由于 = ( , ),且 = 4 2 + 4 > 0,
所以方程 2 + 2 + 1 = 0的两根分别为 , ,且 + = 2 , = 1,
又[ ( ) ( )]2 ≤ 10,即( 2
2
+1 2
) ≤ 10,
+1
将 + = 2 , = 1代入整理得:
1 1 2
3
2 +
3 2 + 3 + 2 1 ( ) 1( ) = × [ ] = × [ ]2 = ( )2 ≤ 10,
4 2+1 2+1 4 ( 2+1)( 2+1) 4 2( ) 4
从而( + )2 4 ≤ 40,
第 5 页,共 9 页
所以 2 9 ≤ 0,解得 3 ≤ ≤ 3,
即实数 的取值范围为[ 3,3].
2
17.【答案】解:(1)根据题意得, = ,故 = , = = 2,故 ( ) = 2 (2 + ).
4 4
5 5
将 ( , 2)代入,得2 × ( ) + = + 2 ( ∈ ),解得 = +2 ( ∈ )
12 12 6
,
又| | < ,故 = 2 6.
(2) 2 3 2 2 依题意, ( ) = 2 [ ( ) ] = 2 ( ).
3 4 6 3 3
函数 = ( ) 在区间[ , ]的零点个数即为函数 ( )的图象与直线 = 在[ , ]2 2 上的交点个数.
2 2 4
当 ∈ [ , ]2 时, ∈ [ , ],结合余弦函数图象可知, 3 3 3 3
当 ∈ [ , ]时, ( )单调递减,当 ∈ ( , ]时, ( )2 2 2 单调递增,
且 ( ) = 1, ( ) = 1, ( ) = 22 2 ,
作出函数 ( )在[ , ]2 上的大致图象如图所示.
观察可知,当 = 2或 1 < ≤ 1时, = ( ) 有1个零点;
当 2 < ≤ 1时, = ( ) 有2个零点;
当 < 2或 > 1时, = ( ) 有0个零点.
18.【答案】解:(1)由题意,得 ( ) = 2√ 3 2 2 + 1 = √ 3 2 + 2 = 2 (2 + ).
6
令2 + = , ∈ ,得 = + , ∈ ,
6 12 2
∴曲线 = ( )的对称中心为( + , 0), ∈ .
12 2
(2) ( ) = 2 ( + ) = 2,即sin( + ) = 1.
2 6 6
∵ 是锐角三角形 的内角,
∴ + = ,
6 2
第 6 页,共 9 页
∴ = .
3
+ + 2√ 3 2√ 3 2√ 3 3 √ 3
由正弦定理得 = = ( + ) = [sin( + )+ ] = × ( + ) =
3 3 3 2 2
2 ( + ).
6
0 < <
在锐角三角形 中,{ 22 ,
0 < <
3 2
解得 ∈ ( , ),
6 2
2
∴ + ∈ ( , ),
6 3 3
√ 3
∴ sin( + ) ∈ ( , 1].
6 2
+
即√ 3 < ≤ 2,
∴ ≥ 2,即实数 的最小值为2.
19.【答案】解:(1)设∠ = ,(0 < < );
2
∴ = , = ;
∵ = 2 ,
∴ ═2 = 2 ;
√ 2
∴当 = 时,即 = 时,矩形面积最大为1;
4 2
2
(2)依题意可得:椭圆方程为: + 2 = 1, ( ≥ 0);
4
设:点 坐标为( , )即: = , = ;
∴ = 2 = 2 ;
∵点 为椭圆上的点;
2
∴ + 2 = 1;
4
2 2
∵ + 2 ≥ 2√
2 = ;
4 4
1
∴ ≤ 1,当且仅当 = = 时取等号;
2 2
∴ ≤ 2;
即矩形面积最大为2;当 = √ 2时取等号;
第 7 页,共 9 页
20.【答案】解:(1)2014年至2019年每年该地人口的增长数量为2385 2082 = 303千人,
3135 2082 = 53,2203 2135 = 68,2276 2203= 73,2339 2276 = 63,2385 2339 = 46,
由上述数据可得从2014年到2019年每年人口增长数量呈先增加后减少的变化趋势,每一年人口总数呈逐渐
递增的变化趋势,
450
(2)由 ( ) = 2000+
4.4878 0.6554
,
+1
∵ ( )的反函数为 ( ),
450
∴ 2400 = 2000+
4.4878 0.6654
,
+1
∴ 4.4878 0.6554
450
+1 = ,
400
∴ 4.4878 0.6554
1
= ,
8
两边取对数可得 4.4878 0.6554 = 8,
4.4878+ 8 35.9024
∴ = = ≈ 5.5,
0.6554 0.6554
∴ (2400) = 5.5.
其实际意义为:可根据数学模型预测人口数量增长规律,及提供有效数据,即经过半年时间,该地人口数
量人数即增长到2400千人.
21.【答案】解:(1) ∵ , , 成等差数列,
∴ = ,
3
∵
3
· = ,
2
3
∴ ( ) = ,
2
1 3 1
∴ = , ,即 = 3.
2 2 2
∵ = √ 3, 2 = 2 + 2 2 ,
∴ 2 + 2 = 3,即( + )2 3 = 3,
∴ ( + )2 = 12,所以 + = 2√ 3;
2 √ 3 1
(2)2 = 2 ( ) = 2( + ) = √ 3 ,
3 2 2
2
∵ 0 < < ,
3
第 8 页,共 9 页
√ 3
∴ √ 3 ∈ ( ,√ 3),
2
√ 3
∴ 2 的取值范围是( , √ 3).
2
第 9 页,共 9 页
同课章节目录
