2.1多边形(1) 课件(共31张PPT)
文档属性
| 名称 | 2.1多边形(1) 课件(共31张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-09 21:27:21 | ||
图片预览






文档简介
(共31张PPT)
第一章 直角三角形
2.1多边形(1)
01
教学目标
02
新知导入
03
新知讲解
04
课堂练习
05
课堂小结
06
作业布置
01
教学目标
01
02
03
通过探索多边形内角和公式,让学生逐步从实验几何过渡到论证几何.
多边形内角和定理及其应用.
02
新知导入
欣赏图片
03
新知探究
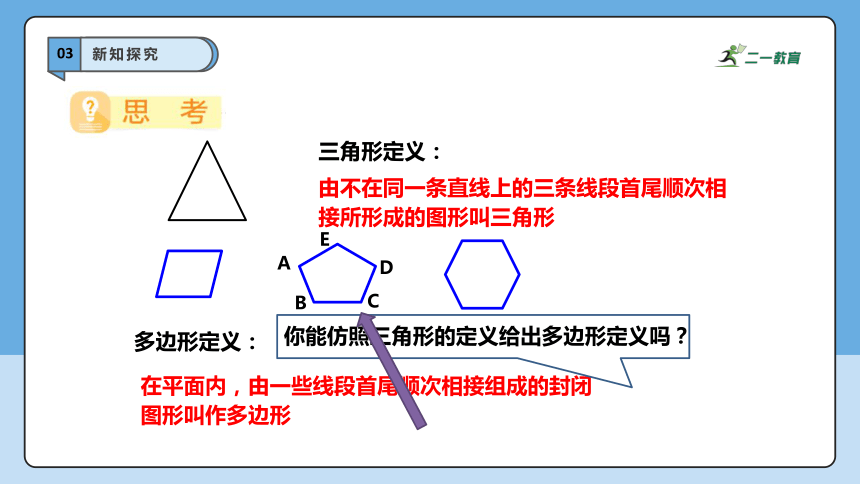
由不在同一条直线上的三条线段首尾顺次相接所形成的图形叫三角形
三角形定义:
多边形定义:
你能仿照三角形的定义给出多边形定义吗?
在平面内,由一些线段首尾顺次相接组成的封闭图形叫作多边形
A
B
C
D
E
03
新知探究
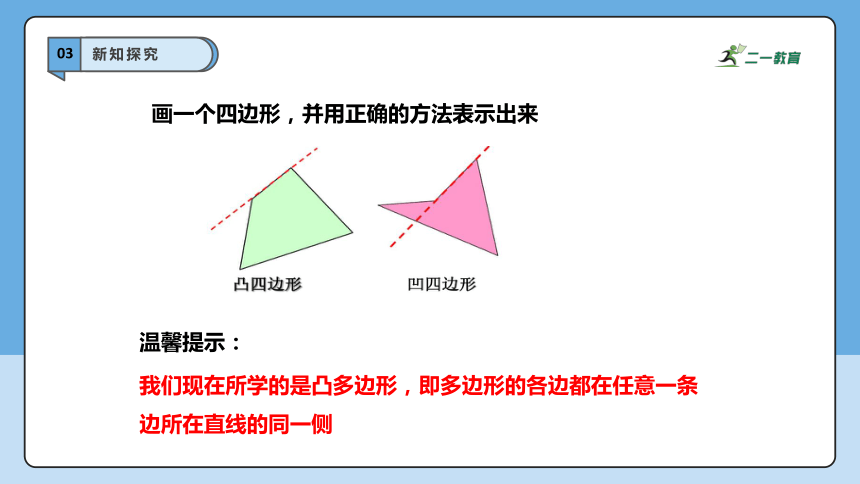
画一个四边形,并用正确的方法表示出来
温馨提示:
我们现在所学的是凸多边形,即多边形的各边都在任意一条边所在直线的同一侧
03
新知讲解
新知讲解
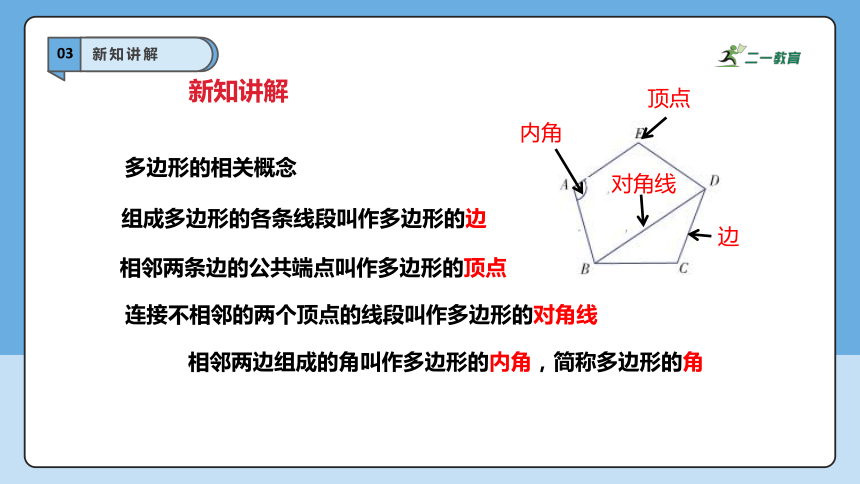
多边形的相关概念
组成多边形的各条线段叫作多边形的边
相邻两条边的公共端点叫作多边形的顶点
连接不相邻的两个顶点的线段叫作多边形的对角线
相邻两边组成的角叫作多边形的内角,简称多边形的角
顶点
内角
边
对角线
03
新知讲解
在平面内,边相等、角也都相等的多边形叫做正多边形
正三角形
正方形
正五边形
正六边形
正八边形
各边相等,各内角也相等的多边形叫做正多边形
各边相等
正多边形
03
新知讲解
n边形有_____个顶点,
_____条边,
_____个内角,
_____条对角线。
n
n
n
总结
?
03
新知讲解
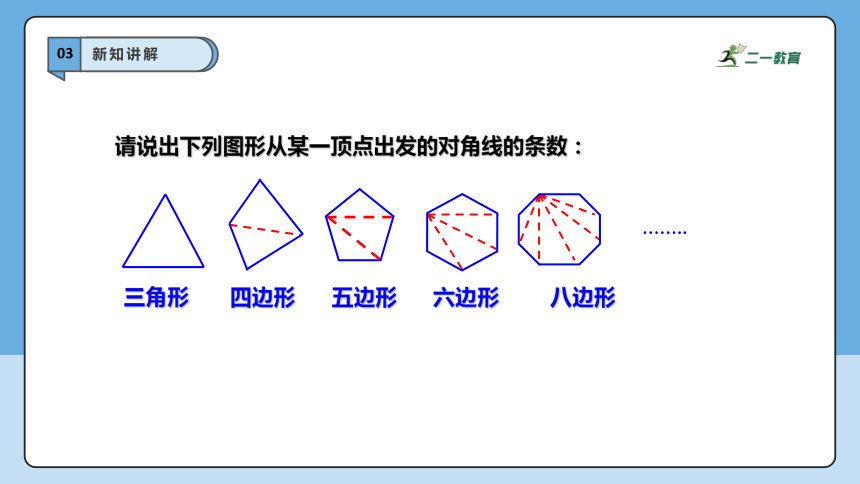
三角形
六边形
四边形
八边形
……..
五边形
请说出下列图形从某一顶点出发的对角线的条数:
03
新知讲解
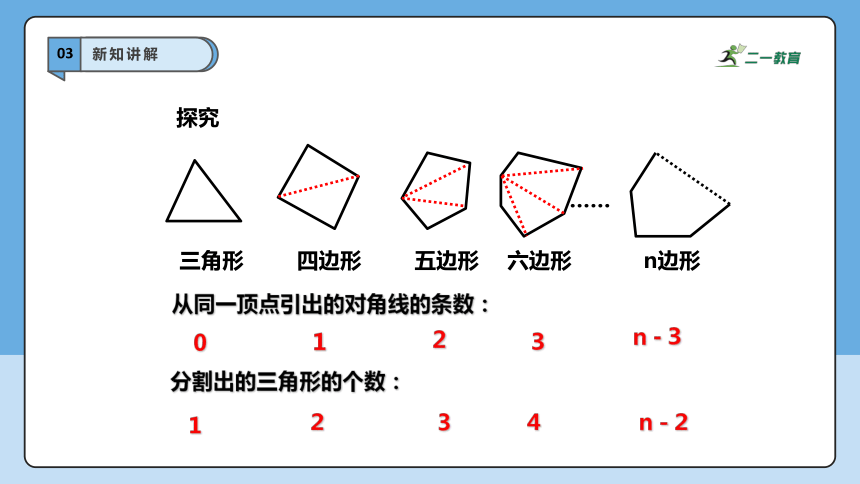
从同一顶点引出的对角线的条数:
1
2
3
n-3
分割出的三角形的个数:
2
3
4
n-2
0
1
n边形
……
三角形
四边形
五边形
六边形
探究
03
新知讲解
n边形从一个顶点出发的对角线条数为: 条(n≥3)
(n-3)
n边形共有对角线 条(n≥3)
总结
对角线是解决多边形问题的常用辅助线
多边形问题
(未知)
三角形问题
(已知)
转化
03
新知讲解
三角形的内角和等于180 °,四边形的内角和是多少度呢?
03
新知讲解
从四边形的一个顶点出发,
可以作_____条对角线,它们将
四边形分为 个三角形,
四边形的内角和等于
180°×____= °.
1
2
2
360
A
B
C
D
03
新知讲解
从五边形的一个顶点出发,
可以作_____条对角线,它们将
五边形分为 个三角形,
五边形的内角和等于
180°×____= °.
2
3
540
3
03
新知讲解
从六边形的一个顶点出发,
可以作_____条对角线,它们将
六边形分为 个三角形,
六边形的内角和等于
180°×____= °.
3
4
720
4
03
新知讲解
总结
3
4
5
6
······
······
······
n 边形
八边形
七边形
六边形
五边形
多边形内角和
分割出三角形的个数
多边形
······
图形
边数
······
5
6
7
8
n
n-2
(5-2) ×180°
(6-2) ×180°
(7-2) ×180°
(8-2) ×180°
(n-2) ×180°
03
新知讲解
你能从五边形、六边形、七边形的内角和的研究过程获得启发,发现多边形的内角和与边数的关系吗?能证明你发现的结论吗?
03
新知讲解
从n 边形的一个顶点出发,可以作(n -3)条对角线,它们将n 边形分为(n -2)个三角形,这(n -2)个三角形的内角和就是n 边形的内角和,所以,n 边形的内角和等于(n -2)×180°.
归纳
03
新知讲解
动脑筋
你还可以用其他方法探究n边形的内角和公式吗?
在n边形内任取一点O,与多边形各顶点连接, 把n边形分成n个三角形,用n个三角形的内角和 n· 180°减去中心的周角360°,得n边形的内角和为(n-2)· 180°.
03
新知讲解
在n边形的边上任取一点O,与多边形各顶点连接, 把n边形分成n个三角形,用n个三角形的内角和 n· 180°减去中心的平角180°,得n边形的内角和为(n-2)· 180°.
新课探究
例1
(1)十边形的内角和是多少度?
(2)一个多边形的内角和等于1980°,它是几边形?
解:(1)十边形的内角和是(10-2)×180°=1440°.
(2)设这个多边形的边数为 n, 则
(n-2)×180°=1980°,
解得n=13.
所以这是一个十三边形.
04
课堂练习
【知识技能类作业】必做题:
1、一个多边形的内角和为1 440°,则此多边形的边数为( )
A.9 B.10 C.11 D.12
2、将一个n边形变成n+1边形,内角和将( )
A.减少180° B.增加90°
C.增加180° D.增加360°
B
C
04
课堂练习
【知识技能类作业】选做题:
3.凸n边形的对角线的条数记作an(n≥4),例如:a4=2,那么:①a5=__________;②a6-a5=__________;
③an+1-an=______(n≥4,用含n的代数式表示).
5
n-1
4
04
课堂练习
【综合拓展类作业】
4、某同学在求多边形的内角和时,多算了一个内角的度数,求得内角和为1560°,问这个内角是多少度?这个多边形的边数是多少?
解:设这个多边形的边数为n,多算的这个内角为α,则有:
(n-2)·180°+α=1 560°.
α=1560°-(n-2)·180°.
显然:0°<α<180°,
所以0°<1 560°-(n-2)·180°<180°.解得9因此n=10.α=1 560°-(10-2)·180°=120°.
答:这个内角是120°,这个多边形的边数是10.
05
课堂小结
多边形
一、多边形的有关概念
二、多边形的内角和公式
多边形内角和
三角形内角和
转化
n边形的内角和等于(n-2) ·180°
三、多边形的内角和公式的应用
(1)已知边数如何求内角和
(2)已知内角和如何求边数
06
作业布置
【知识技能类作业】必做题:
1.如图,在四边形ABCD中,∠A=45°.直线l与边AB、AD分别相交于点M、N,则∠1+∠2=__________.
72°
06
作业布置
【知识技能类作业】选做题:
2.已知两个多边形的内角和为1440°,且两多边形的边数之比为1︰3,求它们的边数分别是多少?
解:设它们的边数分别是x,y.由题意得:
(x-2)·180+(y -2)·180=1440
x : y=1 : 3
解之得 x =3
y =9
答:它们的边数分别是3和9。
06
作业布置
【综合拓展类作业】
3.如图,求∠1+∠2+∠3+∠4+∠5+∠6+∠7的度数.
解:连接∠3与∠7的顶点,
8
9
观察图形可知,∠1+∠2=∠8+∠9.
由五边形内角和可知∠3+∠4+∠5+∠6+∠7+∠8+∠9=540°.
∴∠1+∠2+∠3+∠4+∠5+∠6+∠7=540°.
Thanks!
https://www.21cnjy.com/recruitment/home/fine
第一章 直角三角形
2.1多边形(1)
01
教学目标
02
新知导入
03
新知讲解
04
课堂练习
05
课堂小结
06
作业布置
01
教学目标
01
02
03
通过探索多边形内角和公式,让学生逐步从实验几何过渡到论证几何.
多边形内角和定理及其应用.
02
新知导入
欣赏图片
03
新知探究
由不在同一条直线上的三条线段首尾顺次相接所形成的图形叫三角形
三角形定义:
多边形定义:
你能仿照三角形的定义给出多边形定义吗?
在平面内,由一些线段首尾顺次相接组成的封闭图形叫作多边形
A
B
C
D
E
03
新知探究
画一个四边形,并用正确的方法表示出来
温馨提示:
我们现在所学的是凸多边形,即多边形的各边都在任意一条边所在直线的同一侧
03
新知讲解
新知讲解
多边形的相关概念
组成多边形的各条线段叫作多边形的边
相邻两条边的公共端点叫作多边形的顶点
连接不相邻的两个顶点的线段叫作多边形的对角线
相邻两边组成的角叫作多边形的内角,简称多边形的角
顶点
内角
边
对角线
03
新知讲解
在平面内,边相等、角也都相等的多边形叫做正多边形
正三角形
正方形
正五边形
正六边形
正八边形
各边相等,各内角也相等的多边形叫做正多边形
各边相等
正多边形
03
新知讲解
n边形有_____个顶点,
_____条边,
_____个内角,
_____条对角线。
n
n
n
总结
?
03
新知讲解
三角形
六边形
四边形
八边形
……..
五边形
请说出下列图形从某一顶点出发的对角线的条数:
03
新知讲解
从同一顶点引出的对角线的条数:
1
2
3
n-3
分割出的三角形的个数:
2
3
4
n-2
0
1
n边形
……
三角形
四边形
五边形
六边形
探究
03
新知讲解
n边形从一个顶点出发的对角线条数为: 条(n≥3)
(n-3)
n边形共有对角线 条(n≥3)
总结
对角线是解决多边形问题的常用辅助线
多边形问题
(未知)
三角形问题
(已知)
转化
03
新知讲解
三角形的内角和等于180 °,四边形的内角和是多少度呢?
03
新知讲解
从四边形的一个顶点出发,
可以作_____条对角线,它们将
四边形分为 个三角形,
四边形的内角和等于
180°×____= °.
1
2
2
360
A
B
C
D
03
新知讲解
从五边形的一个顶点出发,
可以作_____条对角线,它们将
五边形分为 个三角形,
五边形的内角和等于
180°×____= °.
2
3
540
3
03
新知讲解
从六边形的一个顶点出发,
可以作_____条对角线,它们将
六边形分为 个三角形,
六边形的内角和等于
180°×____= °.
3
4
720
4
03
新知讲解
总结
3
4
5
6
······
······
······
n 边形
八边形
七边形
六边形
五边形
多边形内角和
分割出三角形的个数
多边形
······
图形
边数
······
5
6
7
8
n
n-2
(5-2) ×180°
(6-2) ×180°
(7-2) ×180°
(8-2) ×180°
(n-2) ×180°
03
新知讲解
你能从五边形、六边形、七边形的内角和的研究过程获得启发,发现多边形的内角和与边数的关系吗?能证明你发现的结论吗?
03
新知讲解
从n 边形的一个顶点出发,可以作(n -3)条对角线,它们将n 边形分为(n -2)个三角形,这(n -2)个三角形的内角和就是n 边形的内角和,所以,n 边形的内角和等于(n -2)×180°.
归纳
03
新知讲解
动脑筋
你还可以用其他方法探究n边形的内角和公式吗?
在n边形内任取一点O,与多边形各顶点连接, 把n边形分成n个三角形,用n个三角形的内角和 n· 180°减去中心的周角360°,得n边形的内角和为(n-2)· 180°.
03
新知讲解
在n边形的边上任取一点O,与多边形各顶点连接, 把n边形分成n个三角形,用n个三角形的内角和 n· 180°减去中心的平角180°,得n边形的内角和为(n-2)· 180°.
新课探究
例1
(1)十边形的内角和是多少度?
(2)一个多边形的内角和等于1980°,它是几边形?
解:(1)十边形的内角和是(10-2)×180°=1440°.
(2)设这个多边形的边数为 n, 则
(n-2)×180°=1980°,
解得n=13.
所以这是一个十三边形.
04
课堂练习
【知识技能类作业】必做题:
1、一个多边形的内角和为1 440°,则此多边形的边数为( )
A.9 B.10 C.11 D.12
2、将一个n边形变成n+1边形,内角和将( )
A.减少180° B.增加90°
C.增加180° D.增加360°
B
C
04
课堂练习
【知识技能类作业】选做题:
3.凸n边形的对角线的条数记作an(n≥4),例如:a4=2,那么:①a5=__________;②a6-a5=__________;
③an+1-an=______(n≥4,用含n的代数式表示).
5
n-1
4
04
课堂练习
【综合拓展类作业】
4、某同学在求多边形的内角和时,多算了一个内角的度数,求得内角和为1560°,问这个内角是多少度?这个多边形的边数是多少?
解:设这个多边形的边数为n,多算的这个内角为α,则有:
(n-2)·180°+α=1 560°.
α=1560°-(n-2)·180°.
显然:0°<α<180°,
所以0°<1 560°-(n-2)·180°<180°.解得9
答:这个内角是120°,这个多边形的边数是10.
05
课堂小结
多边形
一、多边形的有关概念
二、多边形的内角和公式
多边形内角和
三角形内角和
转化
n边形的内角和等于(n-2) ·180°
三、多边形的内角和公式的应用
(1)已知边数如何求内角和
(2)已知内角和如何求边数
06
作业布置
【知识技能类作业】必做题:
1.如图,在四边形ABCD中,∠A=45°.直线l与边AB、AD分别相交于点M、N,则∠1+∠2=__________.
72°
06
作业布置
【知识技能类作业】选做题:
2.已知两个多边形的内角和为1440°,且两多边形的边数之比为1︰3,求它们的边数分别是多少?
解:设它们的边数分别是x,y.由题意得:
(x-2)·180+(y -2)·180=1440
x : y=1 : 3
解之得 x =3
y =9
答:它们的边数分别是3和9。
06
作业布置
【综合拓展类作业】
3.如图,求∠1+∠2+∠3+∠4+∠5+∠6+∠7的度数.
解:连接∠3与∠7的顶点,
8
9
观察图形可知,∠1+∠2=∠8+∠9.
由五边形内角和可知∠3+∠4+∠5+∠6+∠7+∠8+∠9=540°.
∴∠1+∠2+∠3+∠4+∠5+∠6+∠7=540°.
Thanks!
https://www.21cnjy.com/recruitment/home/fine
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
