6.3正方形的性质与判定 同步练习(含答案)鲁教版(五四学制)数学八年级下册
文档属性
| 名称 | 6.3正方形的性质与判定 同步练习(含答案)鲁教版(五四学制)数学八年级下册 |  | |
| 格式 | docx | ||
| 文件大小 | 342.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-11 19:19:25 | ||
图片预览


文档简介
6.3正方形的性质与判定 同步练习
学校:___________姓名:___________班级:___________学号:___________
一、单选题
1.如图,在矩形中,角线与相交于点O,添加下列条不能判定矩形是正方形的是( )
A. B. C. D.平分
2.“方胜”是中国古代妇女的一种发饰,其图案由两个全等正方形相叠组成,寓意是同心吉祥.如图,将边长为的正方形沿对角线方向平移得到正方形,形成一个“方胜”图案,则点D,之间的距离为( )
A. B. C. D.
3.如图,正方形中,点E、F分别在边、上,,于H.若,,则的长是( )
A.3 B.4 C.6 D.8
4.如图,边长为5的正方形中,点E、F分别在边、上,连接、、.已知平分,,则的长为( )
A.2 B.4 C. D.
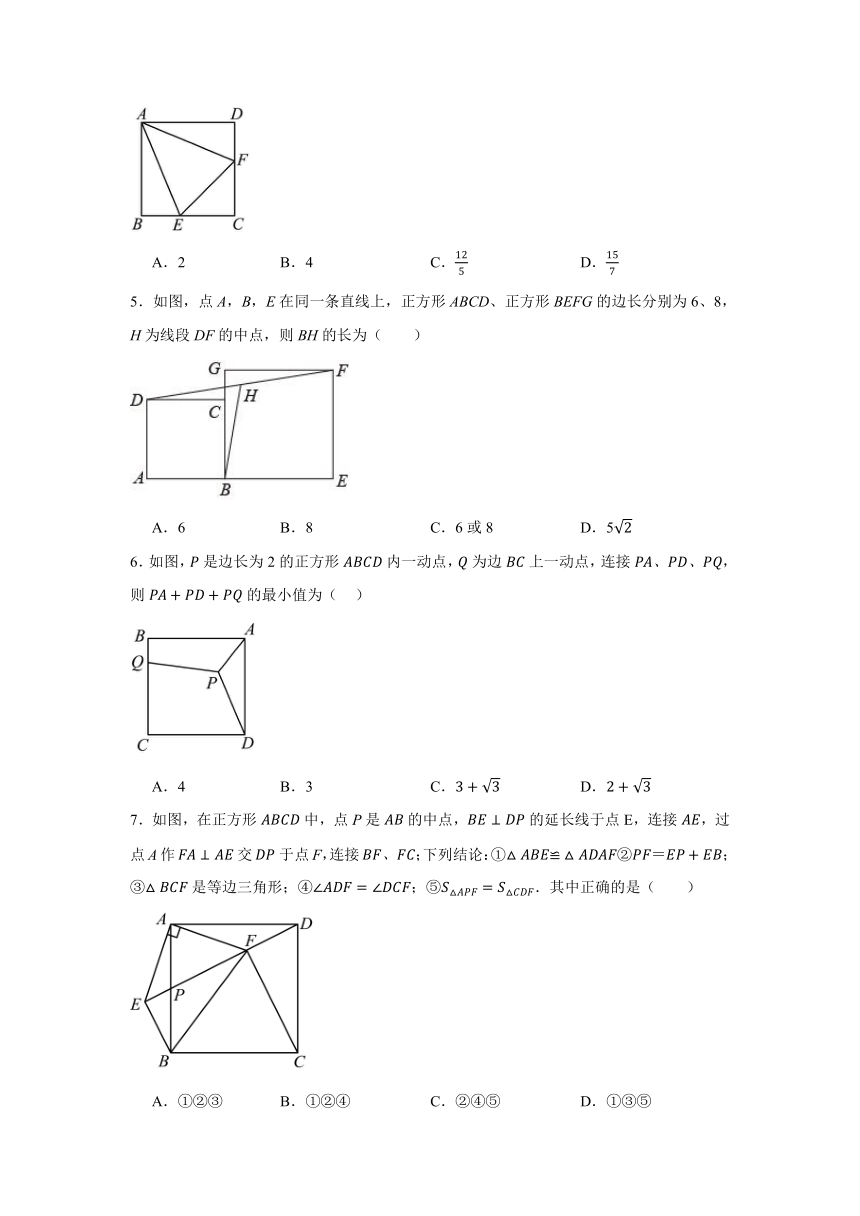
5.如图,点A,B,E在同一条直线上,正方形ABCD、正方形BEFG的边长分别为6、8,H为线段DF的中点,则BH的长为( )
A.6 B.8 C.6或8 D.5
6.如图,是边长为2的正方形内一动点,为边上一动点,连接,则的最小值为( )
A.4 B.3 C. D.
7.如图,在正方形中,点P是的中点,的延长线于点E,连接,过点A作交于点F,连接;下列结论:①②;③是等边三角形;④;⑤.其中正确的是( )
A.①②③ B.①②④ C.②④⑤ D.①③⑤
二、填空题
8.正方形的一条对角线长为3,则这个正方形的面积是 .
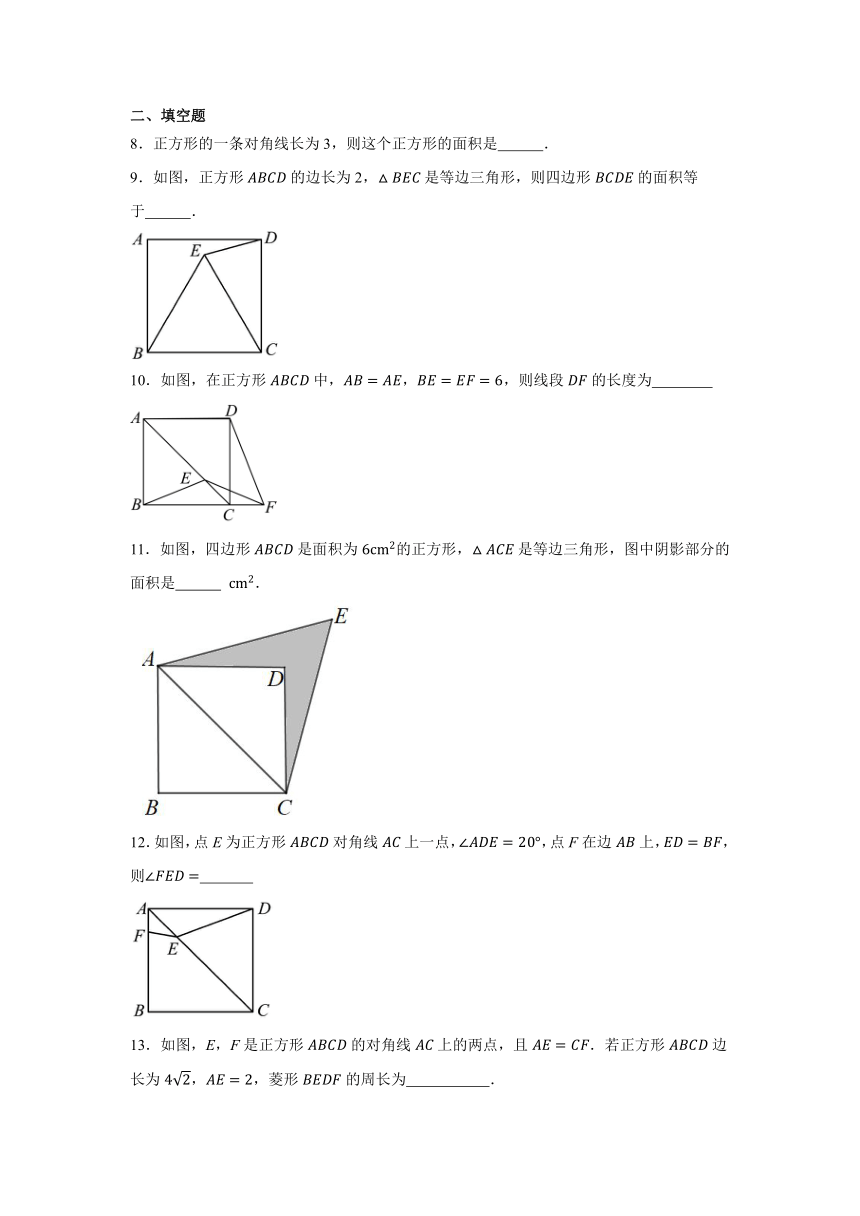
9.如图,正方形的边长为2,是等边三角形,则四边形的面积等于 .
10.如图,在正方形中,,,则线段的长度为
11.如图,四边形是面积为的正方形,是等边三角形,图中阴影部分的面积是 .
12.如图,点E为正方形对角线上一点,,点F在边上,,则
13.如图,E,F是正方形的对角线上的两点,且.若正方形边长为,,菱形的周长为 .
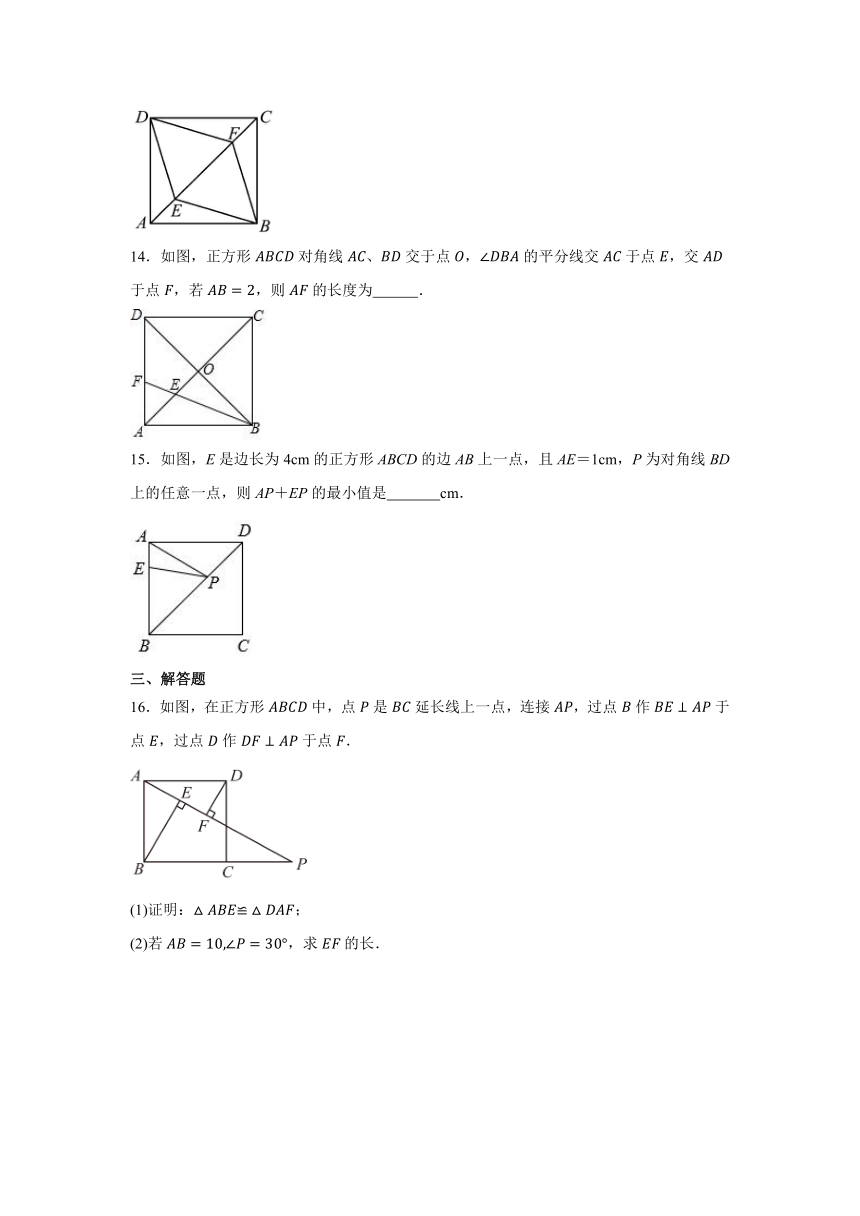
14.如图,正方形对角线、交于点,的平分线交于点,交于点,若,则的长度为 .
15.如图,E是边长为4cm的正方形ABCD的边AB上一点,且AE=1cm,P为对角线BD上的任意一点,则AP+EP的最小值是 cm.
三、解答题
16.如图,在正方形中,点是延长线上一点,连接,过点作于点,过点作于点.
(1)证明:;
(2)若,求的长.
17.如图,在正方形ABCD中,点F为CD上一点,BF与AC交于点E.
(1)的大小=______°;
(2)求证:≌;
(3)若,则的大小=______°.
18.在正方形中,点、分别在边和上,且满足是等边三角形,连接交于点.
(1)求证:;
(2)若等边边长为,求的长.
19.请用无刻度的直尺作图
(1)在图1中,已知点是正方形ABCD边的中点,分别画出BC,CD,DA的中点F,G,H;
(2)图2是正方形,是对角线上任意一点,以为边画一个菱形.
20.如图,在正方形中,边长为3,点M,N是边,上两点,
且,连接,;
(1)则与的数量关系是__________,位置关系是__________;
(2)若点E,F分别是与的中点,计算的长;
(3)延长至P,连接,若,试求的长.
参考答案
1.B
2.D
3.D
4.D
5.D
6.D
7.B
8.
9.
10.
11.
12.
13.
14.
15.5
16.(1)证明:∵四边形是正方形,
∴,
∵,
∴,
∴,
∴,
∴;
(2)解:∵四边形是正方形,,
∴,
∴,
∵,
∴,
在中,由勾股定理,得
,
∵,
∴,
∴.
17.(1)解:∵四边形ABCD是正方形,
∴,
(2)证明:∵四边形ABCD是正方形
∴,
在和中
∵
∴≌(SAS).
(3)解:∵≌
∴
∵
∴
18.(1)证明:正方形,
∴,=90°,.
是等边三角形,
.
.
.
.
(2)由(1)得,CE=CF,AE=AF=2,
垂直平分.
.
,
∵∠ECF=90°,EG=GF,
∴,
.
19.如图,点F、G、H即为所求,
(2)如图所示:四边形AECF即为所求的菱形.
20.解:(1)设CM与DN交于点Q,
∵四边形ABCD是正方形,
∴BC=CD,∠B=∠NCD=90°,
∵,
∴△BCM≌△CDN,
∴CM=DN,∠BCM=∠CDN,
∵∠BCM+∠MCD=90°,
∴∠CDN+∠MCD=90°,
∴∠CQD=90°,
∴,
(2)连并延长交于G,
∵BC∥AD,
∴∠ENC=∠EDG,
∵NE=DE,∠NEC=∠GED,
∴,NC=GD=1,
又∵,
∴,
∵正方形的边长为3,,
∴
∴
(3)过点B作于点H,
,
∵,
∴,
,
∵,
∴,
∴,
∴;
学校:___________姓名:___________班级:___________学号:___________
一、单选题
1.如图,在矩形中,角线与相交于点O,添加下列条不能判定矩形是正方形的是( )
A. B. C. D.平分
2.“方胜”是中国古代妇女的一种发饰,其图案由两个全等正方形相叠组成,寓意是同心吉祥.如图,将边长为的正方形沿对角线方向平移得到正方形,形成一个“方胜”图案,则点D,之间的距离为( )
A. B. C. D.
3.如图,正方形中,点E、F分别在边、上,,于H.若,,则的长是( )
A.3 B.4 C.6 D.8
4.如图,边长为5的正方形中,点E、F分别在边、上,连接、、.已知平分,,则的长为( )
A.2 B.4 C. D.
5.如图,点A,B,E在同一条直线上,正方形ABCD、正方形BEFG的边长分别为6、8,H为线段DF的中点,则BH的长为( )
A.6 B.8 C.6或8 D.5
6.如图,是边长为2的正方形内一动点,为边上一动点,连接,则的最小值为( )
A.4 B.3 C. D.
7.如图,在正方形中,点P是的中点,的延长线于点E,连接,过点A作交于点F,连接;下列结论:①②;③是等边三角形;④;⑤.其中正确的是( )
A.①②③ B.①②④ C.②④⑤ D.①③⑤
二、填空题
8.正方形的一条对角线长为3,则这个正方形的面积是 .
9.如图,正方形的边长为2,是等边三角形,则四边形的面积等于 .
10.如图,在正方形中,,,则线段的长度为
11.如图,四边形是面积为的正方形,是等边三角形,图中阴影部分的面积是 .
12.如图,点E为正方形对角线上一点,,点F在边上,,则
13.如图,E,F是正方形的对角线上的两点,且.若正方形边长为,,菱形的周长为 .
14.如图,正方形对角线、交于点,的平分线交于点,交于点,若,则的长度为 .
15.如图,E是边长为4cm的正方形ABCD的边AB上一点,且AE=1cm,P为对角线BD上的任意一点,则AP+EP的最小值是 cm.
三、解答题
16.如图,在正方形中,点是延长线上一点,连接,过点作于点,过点作于点.
(1)证明:;
(2)若,求的长.
17.如图,在正方形ABCD中,点F为CD上一点,BF与AC交于点E.
(1)的大小=______°;
(2)求证:≌;
(3)若,则的大小=______°.
18.在正方形中,点、分别在边和上,且满足是等边三角形,连接交于点.
(1)求证:;
(2)若等边边长为,求的长.
19.请用无刻度的直尺作图
(1)在图1中,已知点是正方形ABCD边的中点,分别画出BC,CD,DA的中点F,G,H;
(2)图2是正方形,是对角线上任意一点,以为边画一个菱形.
20.如图,在正方形中,边长为3,点M,N是边,上两点,
且,连接,;
(1)则与的数量关系是__________,位置关系是__________;
(2)若点E,F分别是与的中点,计算的长;
(3)延长至P,连接,若,试求的长.
参考答案
1.B
2.D
3.D
4.D
5.D
6.D
7.B
8.
9.
10.
11.
12.
13.
14.
15.5
16.(1)证明:∵四边形是正方形,
∴,
∵,
∴,
∴,
∴,
∴;
(2)解:∵四边形是正方形,,
∴,
∴,
∵,
∴,
在中,由勾股定理,得
,
∵,
∴,
∴.
17.(1)解:∵四边形ABCD是正方形,
∴,
(2)证明:∵四边形ABCD是正方形
∴,
在和中
∵
∴≌(SAS).
(3)解:∵≌
∴
∵
∴
18.(1)证明:正方形,
∴,=90°,.
是等边三角形,
.
.
.
.
(2)由(1)得,CE=CF,AE=AF=2,
垂直平分.
.
,
∵∠ECF=90°,EG=GF,
∴,
.
19.如图,点F、G、H即为所求,
(2)如图所示:四边形AECF即为所求的菱形.
20.解:(1)设CM与DN交于点Q,
∵四边形ABCD是正方形,
∴BC=CD,∠B=∠NCD=90°,
∵,
∴△BCM≌△CDN,
∴CM=DN,∠BCM=∠CDN,
∵∠BCM+∠MCD=90°,
∴∠CDN+∠MCD=90°,
∴∠CQD=90°,
∴,
(2)连并延长交于G,
∵BC∥AD,
∴∠ENC=∠EDG,
∵NE=DE,∠NEC=∠GED,
∴,NC=GD=1,
又∵,
∴,
∵正方形的边长为3,,
∴
∴
(3)过点B作于点H,
,
∵,
∴,
,
∵,
∴,
∴,
∴;
