1.5.1 有理数的乘方课件
图片预览






文档简介
(共17张PPT)
1.5 有理数的乘方(第1课时)
1.5.1 有理数的乘方
义务教育教科书 数学 七年级 上册
学习目标
1.理解并掌握有理数乘方的意义,知道幂、底数、指数的概念
2.能够正确进行有理数的乘方运算
3.在生动的情景中让学生获得有理数乘方的初步体验;培养学生观察、分析、归纳、概括的能力;经历从乘法到乘方的推导过程,从中感受转化的数学思想。
一.创设情境,导入新课
手工拉面是我国的传统面食,制作时,拉面师傅将一团和好的面,揉搓成1根长条后,手握两端用力拉长,然后将长条对折,再拉长,再对折,如此反复操作,连续对折若干次后便成了许多细细的面条.你能算出拉折6次后共有多少根面条吗?
二.新知导学
知识点一:有理数乘方的概念
请同学们认真自学课本41页的内容,然后完成以下填空:
1.边长为2cm的正方形的面积是 记作 读作 或 .
2.棱长是2cm的正方形的体积是 记作 读作 或 .
3.(-2)x(-2)x(-2)x(-2) 记作 读作 .
4.(- )x(- )x(- )x(- )x(- )记作 读作 .
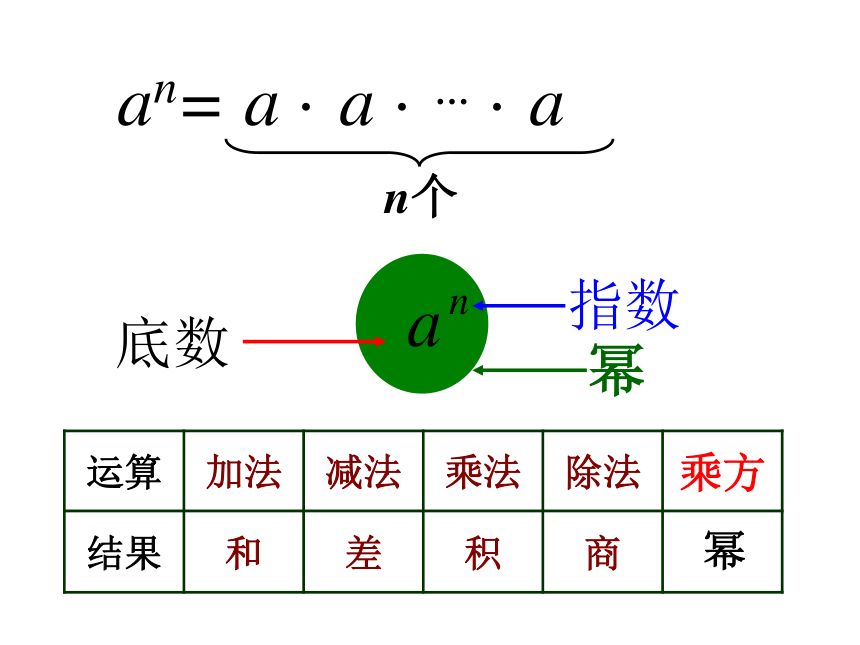
一般地,n个相同的因数a相乘,即
求n个相同因数的积的运算叫做
乘方,乘方的结果叫幂.
,记作 ,读作
a的n次方.
n个
a · a · … · a
底数
指数
幂
运算 加法 减法 乘法 除法 乘方
结果 和 差 积 商
幂
n个
an= a · a · … · a
口答
1.在 中,底数是 指数是 .
2.在 中,底数 是指数是 .
4.把下列各式写成乘方的形式;
x x = .
(-1.2)x(-1.2)x(-1.2)x(-1.2)x(-1.2)= .
(-3)x(-3)x(-3)x(-3)= .
-3x3x3x3= .
知识点二:有理数的乘方运算
例1、计算
①26 ②73 ③(-3)4
④(-4)3 ⑤-34 ⑥ ⑦
⑧ ⑨
你能发现正数幂与负数幂的符号特点吗?
正数的任何次幂都是正数
负数的奇次幂是负数
负数的偶次幂是正数
0的任何正整数次幂都是0
一个数可以看作这个数本身的
一次方
你能迅速判断下列各幂的正负吗?
三 达标测试
A组题
课本42页练习题
(4) ;( )
B组题 判断:(对的画“√”,错的画“×”.)
(1) 32 = 3×2 = 6;( )
(2) (-2)3 = (-3)2; ( )
(3) -32 = (-3)2;( )
(5) ( )
×
32 = 3×3=9
(-2)3=-8;(-3)2=9
-32 =-9; (-3)2=9
-24=-2×2×2×2=-16
×
×
×
×
填空:(用“<”、“>”或“=”)
(1)若a>0,则a2 0,a3 0;
(2)若a<0,则a2 0,a3 0;
(3)若a7<0,则a 0;
(4)若a101<0,则a 0.
>
>
>
<
<
<
B组题
C 组 题
手工拉面是我国的传统面食,制作时,拉面师傅将一团和好的面,揉搓成1根长条后,手握两端用力拉长,然后将长条对折,再拉长,再对折,如此反复操作,连续对折若干次后便成了许多细细的面条.你能算出拉折6次后共有多少根面条吗?
2根
4根
8根
分析:1根面条拉扣1次成2根,拉扣2次成2×2根……
第1次
第2次
第3次
假如一共拉扣了6次,你能算出共有多少根面条吗?
2×2×2×2×2×2=64根
四 小结
1、 乘方是一种特殊的乘法。
2、 底数为负数和分数时候应加括号
3 、 在计算时应首先确定符号。正确确 定负数幂的符号(奇负偶正)
4 、平方=二次方,立方=三次方。
五.作业布置:
必做题:课本47页第1题
选做题:课本48页第11题
1.5 有理数的乘方(第1课时)
1.5.1 有理数的乘方
义务教育教科书 数学 七年级 上册
学习目标
1.理解并掌握有理数乘方的意义,知道幂、底数、指数的概念
2.能够正确进行有理数的乘方运算
3.在生动的情景中让学生获得有理数乘方的初步体验;培养学生观察、分析、归纳、概括的能力;经历从乘法到乘方的推导过程,从中感受转化的数学思想。
一.创设情境,导入新课
手工拉面是我国的传统面食,制作时,拉面师傅将一团和好的面,揉搓成1根长条后,手握两端用力拉长,然后将长条对折,再拉长,再对折,如此反复操作,连续对折若干次后便成了许多细细的面条.你能算出拉折6次后共有多少根面条吗?
二.新知导学
知识点一:有理数乘方的概念
请同学们认真自学课本41页的内容,然后完成以下填空:
1.边长为2cm的正方形的面积是 记作 读作 或 .
2.棱长是2cm的正方形的体积是 记作 读作 或 .
3.(-2)x(-2)x(-2)x(-2) 记作 读作 .
4.(- )x(- )x(- )x(- )x(- )记作 读作 .
一般地,n个相同的因数a相乘,即
求n个相同因数的积的运算叫做
乘方,乘方的结果叫幂.
,记作 ,读作
a的n次方.
n个
a · a · … · a
底数
指数
幂
运算 加法 减法 乘法 除法 乘方
结果 和 差 积 商
幂
n个
an= a · a · … · a
口答
1.在 中,底数是 指数是 .
2.在 中,底数 是指数是 .
4.把下列各式写成乘方的形式;
x x = .
(-1.2)x(-1.2)x(-1.2)x(-1.2)x(-1.2)= .
(-3)x(-3)x(-3)x(-3)= .
-3x3x3x3= .
知识点二:有理数的乘方运算
例1、计算
①26 ②73 ③(-3)4
④(-4)3 ⑤-34 ⑥ ⑦
⑧ ⑨
你能发现正数幂与负数幂的符号特点吗?
正数的任何次幂都是正数
负数的奇次幂是负数
负数的偶次幂是正数
0的任何正整数次幂都是0
一个数可以看作这个数本身的
一次方
你能迅速判断下列各幂的正负吗?
三 达标测试
A组题
课本42页练习题
(4) ;( )
B组题 判断:(对的画“√”,错的画“×”.)
(1) 32 = 3×2 = 6;( )
(2) (-2)3 = (-3)2; ( )
(3) -32 = (-3)2;( )
(5) ( )
×
32 = 3×3=9
(-2)3=-8;(-3)2=9
-32 =-9; (-3)2=9
-24=-2×2×2×2=-16
×
×
×
×
填空:(用“<”、“>”或“=”)
(1)若a>0,则a2 0,a3 0;
(2)若a<0,则a2 0,a3 0;
(3)若a7<0,则a 0;
(4)若a101<0,则a 0.
>
>
>
<
<
<
B组题
C 组 题
手工拉面是我国的传统面食,制作时,拉面师傅将一团和好的面,揉搓成1根长条后,手握两端用力拉长,然后将长条对折,再拉长,再对折,如此反复操作,连续对折若干次后便成了许多细细的面条.你能算出拉折6次后共有多少根面条吗?
2根
4根
8根
分析:1根面条拉扣1次成2根,拉扣2次成2×2根……
第1次
第2次
第3次
假如一共拉扣了6次,你能算出共有多少根面条吗?
2×2×2×2×2×2=64根
四 小结
1、 乘方是一种特殊的乘法。
2、 底数为负数和分数时候应加括号
3 、 在计算时应首先确定符号。正确确 定负数幂的符号(奇负偶正)
4 、平方=二次方,立方=三次方。
五.作业布置:
必做题:课本47页第1题
选做题:课本48页第11题
