北京市延庆区2024-2025学年八年级上学期期末考试数学试卷(含答案)
文档属性
| 名称 | 北京市延庆区2024-2025学年八年级上学期期末考试数学试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 636.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-11 19:11:13 | ||
图片预览



文档简介
北京市延庆区2024-2025学年八年级上学期期末考试
数 学
2025.01
考生须知 1.本试卷共8页,共三道大题,28道小题,满分100分,考试时间120分钟. 2.在试卷和答题卡上正确填写学校名称、姓名和考号. 3.试题答案一律填涂或书写在答题卡上,在试卷上作答无效. 4.在答题卡上,选择题、作图题用2B铅笔作答,其他试题用黑色签字笔作答.
一、选择题(共16分,每小题2分)
第1-8题均有四个选项,符合题意的选项只有一个.
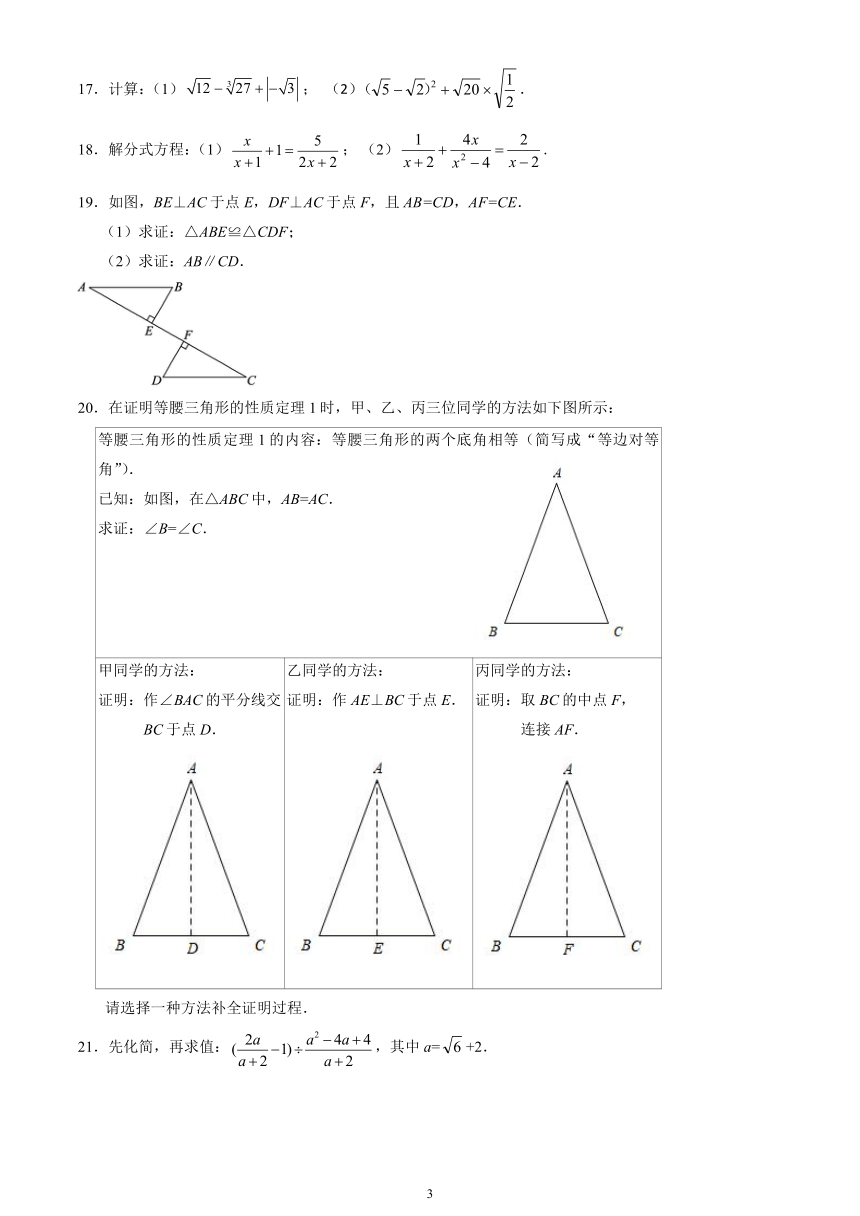
1.下列四个图形是国际数学家大会的会标,其中轴对称图形是
(A) (B) (C) (D)
2.下列事件中,随机事件是
(A)在数轴上取一个点,它表示的数是实数 (B)画一个三角形,它的某边上的高线与中线重合 (C)画一个三角形,它的内角和是180° (D)把长度分别是6,8,9的线段首尾顺次相接,组成了一个直角三角形
3.分式有意义,实数a的取值范围是
(A)a≠3 (B)a≠0 (C)a<3 (D)a≥3
4.三角形的两边长分别为3和6,这个三角形的第三边长可以是
(A)3 (B)6 (C)9 (D)12
5.下列二次根式中,最简二次根式是
(A) (B) (C) (D)
6.下列各式中,计算正确的是
(A) (B)
(C) (D)
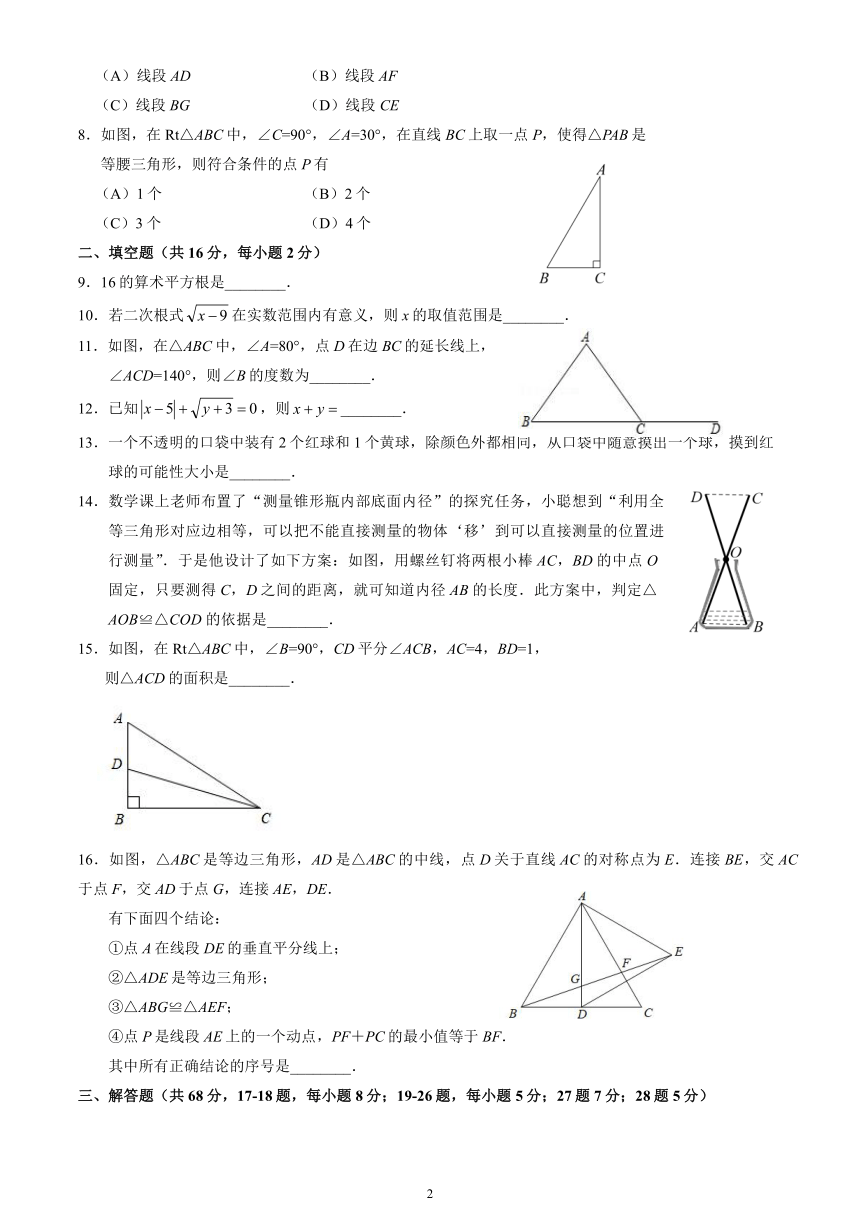
7.如图,在△ABC中,AB边上的高线是
(A)线段AD (B)线段AF
(C)线段BG (D)线段CE
8.如图,在Rt△ABC中,∠C=90°,∠A=30°,在直线BC上取一点P,使得△PAB是
等腰三角形,则符合条件的点P有
(A)1个 (B)2个
(C)3个 (D)4个
二、填空题(共16分,每小题2分)
9.16的算术平方根是________.
10.若二次根式在实数范围内有意义,则x的取值范围是________.
11.如图,在△ABC中,∠A=80°,点D在边BC的延长线上,
∠ACD=140°,则∠B的度数为________.
12.已知,则________.
13.一个不透明的口袋中装有2个红球和1个黄球,除颜色外都相同,从口袋中随意摸出一个球,摸到红球的可能性大小是________.
14.数学课上老师布置了“测量锥形瓶内部底面内径”的探究任务,小聪想到“利用全等三角形对应边相等,可以把不能直接测量的物体‘移’到可以直接测量的位置进行测量”.于是他设计了如下方案:如图,用螺丝钉将两根小棒AC,BD的中点O固定,只要测得C,D之间的距离,就可知道内径AB的长度.此方案中,判定△AOB≌△COD的依据是________.
15.如图,在Rt△ABC中,∠B=90°,CD平分∠ACB,AC=4,BD=1,
则△ACD的面积是________.
16.如图,△ABC是等边三角形,AD是△ABC的中线,点D关于直线AC的对称点为E.连接BE,交AC于点F,交AD于点G,连接AE,DE.
有下面四个结论:
①点A在线段DE的垂直平分线上;
②△ADE是等边三角形;
③△ABG≌△AEF;
④点P是线段AE上的一个动点,PF+PC的最小值等于BF.
其中所有正确结论的序号是________.
三、解答题(共68分,17-18题,每小题8分;19-26题,每小题5分;27题7分;28题5分)
17.计算:(1); (2).
18.解分式方程:(1); (2).
19.如图,BE⊥AC于点E,DF⊥AC于点F,且AB=CD,AF=CE.
(1)求证:△ABE≌△CDF;
(2)求证:AB∥CD.
20.在证明等腰三角形的性质定理1时,甲、乙、丙三位同学的方法如下图所示:
等腰三角形的性质定理1的内容:等腰三角形的两个底角相等(简写成“等边对等角”). 已知:如图,在△ABC中,AB=AC. 求证:∠B=∠C.
甲同学的方法: 证明:作∠BAC的平分线交 BC于点D. 乙同学的方法: 证明:作AE⊥BC于点E. 丙同学的方法: 证明:取BC的中点F, 连接AF.
请选择一种方法补全证明过程.
21.先化简,再求值:,其中a=+2.
22.学习了分式运算后,老师布置了这样一道计算题:,甲、乙两位
同学的解答过程分别如下:
老师发现这两位同学的解答过程都有错误.
请你从两位同学中,选择一位同学的解答过程,分析错因,并加以改正.
(1)我选择________同学的解答过程进行分析(填“甲”或“乙”);
(2)该同学的解答从第________步开始出现错误(填序号),产生错误的原因
可能是 ;
(3)写出正确解答过程.
23.如图,△ABC是等边三角形,D是AB上一点,过点D作BC的平行线交AC于点E.
(1)依题意补全图形;
(2)判断△ADE的形状,并证明.
24.如图,OC是∠AOB的角平分线,点D在射线OA上,点E在射线OB上,点F在射线OC上,连接DF,EF.请你添加一个条件,使△OFD≌△OFE.
小明同学写出以下条件:
①OD=OE, ②∠ODF=∠OEF, ③∠OFD=∠OFE,
④FD=FE, ⑤∠ADF=∠BEF, ⑥∠DFC=∠EFC.
他认为:“添加以上条件中的任何一个,都可以使△OFD≌△OFE.”
(1)小明的说法________(填“正确”或“错误”);
(2)从小明写出的条件中选择一个________(填写序号),使得△OFD≌△OFE,
补全图形,并写出证明过程.
25.列方程解应用题:
远大中学组织学生到距离学校20千米的农耕园体验农耕劳动.有一部分学生骑自行车前往,另一部分学生在骑自行车的学生出发50分钟后,乘汽车沿相同路线行进,结果骑自行车的学生与乘汽车的学生同时到达农耕园.已知汽车速度是自行车速度的3倍,求自行车的速度.
26.尺规作图:
已知:如图1,直线MN和直线MN外一点P.
求作:直线PQ,使直线PQ∥MN.
小智的作图思路如下: ①如何得到两条直线平行? 小智想到,自己学习线与角的时候,有4个定理可以证明两条直线平行,其中有“内错角相等,两条直线平行”. ②如何得到两个角相等? 小智先回顾了线与角的内容,找到了几个定理和1个概念,可以得到两个角相等.小智又回顾了三角形的知识,也发现了几个可以证明两个角相等的定理.最后,小智选择了角平分线的概念和“等边对等角”. ③画出示意图:
④根据示意图,确定作图顺序.
(1)使用直尺和圆规,按照小智的作图思路补全图形1(保留作图痕迹);
(2)完成下面的证明:
证明:
(3)参考小智的作图思路,另外设计一种作法,利用直尺和圆规在图2中完成.
(温馨提示:保留作图痕迹,不用写作法和证明)
27.如图,在Rt△ABC中,∠BAC=90°,AB=AC,AD是△ABC的高,点E是AB的中点,连接CE交AD于点F,过点E作GE⊥CE于点E,交DA的延长线于点G,交BC于点H.
(1)依题意补全图形;
(2)判断∠ECH和∠EGF的数量关系,并证明;
(3)求证:EC=EG.
28.我们给出如下定义:有一条边及这条边所对的角分别相等的两个三角形称为“关联三角形”.例如,下图中的两个三角形是“关联三角形”.
已知:在Rt△ABC中,∠C=90°,∠A=30°,BC=2,AB=4.
(1)下列三角形中,Rt△ABC的“关联三角形”是________(填序号);
(2)若Rt△ABC的“关联三角形”是等腰三角形,则等腰三角形的底边长可以是 ;
(3)若△DEF是Rt△ABC的“关联三角形”,且△DEF的面积是S, 直接写出S的最大值.
参考答案
一、选择题:(共8个小题,每小题2分,共16分)
ABAB DCDB
二、填空题:(共8个小题,每小题2分,共16分)
9. 4 10. x≥9 11.60° 12.2
13. 14.边角边 15.2 16.①②④
三、解答题
17. (本小题满分8分)
(1)
.
(2)
=72+
=7.
(本小题满分8分)
(1)解:方程两边同时乘以,得,
.
.
.
.
.
检验:当时,方程左右两边相等.
所以原分式方程的解为.
(2)解:方程两边同时乘以(x+2)(x2),得
x2+4x=2(x+2).
x2+4x=2x+4.
3x=6.
x=2.
检验:当x=2时,最简公分母(x+2)(x2)=0,原方程中的分式无意义.
所以原方程无解.
19. (本小题满分5分)
(1)证明:∵AF=CE,
∴AE+EF=CF+EF.
∴AE=CF.
∵BE⊥AC于点E,DF⊥AC于点F,
∴∠AEB =∠CFD=90°.
∴△ABE与△CDF是直角三角形.
在Rt△ABE和Rt△CDF中,
∴Rt△ABE≌Rt△CDF(HL) .
(2)证明:∵Rt△ABE≌Rt△CDF,
∴∠A=∠C.
∴AB∥CD.
20. (本小题满分5分)
甲同学的方法:
证明:如图,作∠BAC的平分线交BC于点D.
∴∠BAD=∠CAD.
在△ABD和△ACD中,
∴△ABD≌△ACD(SAS).
∴∠B=∠C.
乙同学的方法:
证明:如图,作AE⊥BC于点E.
∴∠AEB=∠AEC=90°,
在Rt△ABE和Rt△ACE中,
∴Rt△ABE≌Rt△ACE(HL).
∴∠B=∠C.
丙同学的方法:
证明:如图,取BC的中点F,连接AF.
∴BF=CF.
在△ABF和△ACF中,
∴△ABF≌△ACF(SSS).
∴∠B=∠C.
21. (本小题满分5分)
解:原式=
=
=
=
=.
当a=+2时,原式=.
22. (本小题满分5分)
(1)略;
(2)略;
(3)
23. (本小题满分5分)
(1)如图;
(2)△ADE是等边三角形.
证明:∵△ABC是等边三角形,
∴∠A =∠B=∠C=60°.
∵DE∥BC,
∴∠ADE =∠B=60°,
∠AED =∠C=60°.
∴∠A =∠ADE =∠AED.
∴△ADE是等边三角形.
24. (本小题满分5分)
(1)错误;
(2)条件:∠ODF=∠OEF.
证明:∵OC是∠AOB的角平分线,
∴∠DOF=∠EOF.
在△OFD和△OFE中,
∴△OFD≌△OFE(AAS).
说明:添加的条件可以是①,②,③,⑤,⑥.
25. (本小题满分5分)
解:设自行车的速度为x千米/时,则汽车的速度为3x千米/时,由题意得:
,
解得:x=16,
经检验,x=16是原方程的解,且符合题意.
答:自行车的速度为16千米/时.
26. (本小题满分5分)
(1)如图;
(2)①等边对等角;
②内错角相等,两条直线平行;
(3)略.
27. (本小题满分7分)
(1)如图;
(2)数量关系:∠ECH=∠EGF;
证明:∵GE⊥CE于点E,
∴∠GEF =∠CEH=90°.
∴∠ECH+∠GHD=90°.
∵AD是△ABC的高,
∴∠ADB=90°.
∴∠EGF+∠GHD=90°.
∴∠ECH =∠EGF.
(3)证明:连接DE.
∵∠BAC=90°,AB=AC,
∴∠B=∠ACB=45°.
∵AD是△ABC的高,
∴∠DAC=∠DAB=45°.
∴∠B =∠DAB.
∴DA =DB.
∵点E是AB的中点,
∴∠AED=90°,∠ADE=∠BDE=45°.
∴∠ADE =∠EAD.
∴EA=ED.
∵∠GEF=∠AED=90°,
∴∠AEG =∠DEC.
在△EDC与△EAG中,
∴△EDC≌△EAG(AAS).
∴EC=EG.
28. (本小题满分5分)
(1)①③;
(2)2,4,;
(3).
2
数 学
2025.01
考生须知 1.本试卷共8页,共三道大题,28道小题,满分100分,考试时间120分钟. 2.在试卷和答题卡上正确填写学校名称、姓名和考号. 3.试题答案一律填涂或书写在答题卡上,在试卷上作答无效. 4.在答题卡上,选择题、作图题用2B铅笔作答,其他试题用黑色签字笔作答.
一、选择题(共16分,每小题2分)
第1-8题均有四个选项,符合题意的选项只有一个.
1.下列四个图形是国际数学家大会的会标,其中轴对称图形是
(A) (B) (C) (D)
2.下列事件中,随机事件是
(A)在数轴上取一个点,它表示的数是实数 (B)画一个三角形,它的某边上的高线与中线重合 (C)画一个三角形,它的内角和是180° (D)把长度分别是6,8,9的线段首尾顺次相接,组成了一个直角三角形
3.分式有意义,实数a的取值范围是
(A)a≠3 (B)a≠0 (C)a<3 (D)a≥3
4.三角形的两边长分别为3和6,这个三角形的第三边长可以是
(A)3 (B)6 (C)9 (D)12
5.下列二次根式中,最简二次根式是
(A) (B) (C) (D)
6.下列各式中,计算正确的是
(A) (B)
(C) (D)
7.如图,在△ABC中,AB边上的高线是
(A)线段AD (B)线段AF
(C)线段BG (D)线段CE
8.如图,在Rt△ABC中,∠C=90°,∠A=30°,在直线BC上取一点P,使得△PAB是
等腰三角形,则符合条件的点P有
(A)1个 (B)2个
(C)3个 (D)4个
二、填空题(共16分,每小题2分)
9.16的算术平方根是________.
10.若二次根式在实数范围内有意义,则x的取值范围是________.
11.如图,在△ABC中,∠A=80°,点D在边BC的延长线上,
∠ACD=140°,则∠B的度数为________.
12.已知,则________.
13.一个不透明的口袋中装有2个红球和1个黄球,除颜色外都相同,从口袋中随意摸出一个球,摸到红球的可能性大小是________.
14.数学课上老师布置了“测量锥形瓶内部底面内径”的探究任务,小聪想到“利用全等三角形对应边相等,可以把不能直接测量的物体‘移’到可以直接测量的位置进行测量”.于是他设计了如下方案:如图,用螺丝钉将两根小棒AC,BD的中点O固定,只要测得C,D之间的距离,就可知道内径AB的长度.此方案中,判定△AOB≌△COD的依据是________.
15.如图,在Rt△ABC中,∠B=90°,CD平分∠ACB,AC=4,BD=1,
则△ACD的面积是________.
16.如图,△ABC是等边三角形,AD是△ABC的中线,点D关于直线AC的对称点为E.连接BE,交AC于点F,交AD于点G,连接AE,DE.
有下面四个结论:
①点A在线段DE的垂直平分线上;
②△ADE是等边三角形;
③△ABG≌△AEF;
④点P是线段AE上的一个动点,PF+PC的最小值等于BF.
其中所有正确结论的序号是________.
三、解答题(共68分,17-18题,每小题8分;19-26题,每小题5分;27题7分;28题5分)
17.计算:(1); (2).
18.解分式方程:(1); (2).
19.如图,BE⊥AC于点E,DF⊥AC于点F,且AB=CD,AF=CE.
(1)求证:△ABE≌△CDF;
(2)求证:AB∥CD.
20.在证明等腰三角形的性质定理1时,甲、乙、丙三位同学的方法如下图所示:
等腰三角形的性质定理1的内容:等腰三角形的两个底角相等(简写成“等边对等角”). 已知:如图,在△ABC中,AB=AC. 求证:∠B=∠C.
甲同学的方法: 证明:作∠BAC的平分线交 BC于点D. 乙同学的方法: 证明:作AE⊥BC于点E. 丙同学的方法: 证明:取BC的中点F, 连接AF.
请选择一种方法补全证明过程.
21.先化简,再求值:,其中a=+2.
22.学习了分式运算后,老师布置了这样一道计算题:,甲、乙两位
同学的解答过程分别如下:
老师发现这两位同学的解答过程都有错误.
请你从两位同学中,选择一位同学的解答过程,分析错因,并加以改正.
(1)我选择________同学的解答过程进行分析(填“甲”或“乙”);
(2)该同学的解答从第________步开始出现错误(填序号),产生错误的原因
可能是 ;
(3)写出正确解答过程.
23.如图,△ABC是等边三角形,D是AB上一点,过点D作BC的平行线交AC于点E.
(1)依题意补全图形;
(2)判断△ADE的形状,并证明.
24.如图,OC是∠AOB的角平分线,点D在射线OA上,点E在射线OB上,点F在射线OC上,连接DF,EF.请你添加一个条件,使△OFD≌△OFE.
小明同学写出以下条件:
①OD=OE, ②∠ODF=∠OEF, ③∠OFD=∠OFE,
④FD=FE, ⑤∠ADF=∠BEF, ⑥∠DFC=∠EFC.
他认为:“添加以上条件中的任何一个,都可以使△OFD≌△OFE.”
(1)小明的说法________(填“正确”或“错误”);
(2)从小明写出的条件中选择一个________(填写序号),使得△OFD≌△OFE,
补全图形,并写出证明过程.
25.列方程解应用题:
远大中学组织学生到距离学校20千米的农耕园体验农耕劳动.有一部分学生骑自行车前往,另一部分学生在骑自行车的学生出发50分钟后,乘汽车沿相同路线行进,结果骑自行车的学生与乘汽车的学生同时到达农耕园.已知汽车速度是自行车速度的3倍,求自行车的速度.
26.尺规作图:
已知:如图1,直线MN和直线MN外一点P.
求作:直线PQ,使直线PQ∥MN.
小智的作图思路如下: ①如何得到两条直线平行? 小智想到,自己学习线与角的时候,有4个定理可以证明两条直线平行,其中有“内错角相等,两条直线平行”. ②如何得到两个角相等? 小智先回顾了线与角的内容,找到了几个定理和1个概念,可以得到两个角相等.小智又回顾了三角形的知识,也发现了几个可以证明两个角相等的定理.最后,小智选择了角平分线的概念和“等边对等角”. ③画出示意图:
④根据示意图,确定作图顺序.
(1)使用直尺和圆规,按照小智的作图思路补全图形1(保留作图痕迹);
(2)完成下面的证明:
证明:
(3)参考小智的作图思路,另外设计一种作法,利用直尺和圆规在图2中完成.
(温馨提示:保留作图痕迹,不用写作法和证明)
27.如图,在Rt△ABC中,∠BAC=90°,AB=AC,AD是△ABC的高,点E是AB的中点,连接CE交AD于点F,过点E作GE⊥CE于点E,交DA的延长线于点G,交BC于点H.
(1)依题意补全图形;
(2)判断∠ECH和∠EGF的数量关系,并证明;
(3)求证:EC=EG.
28.我们给出如下定义:有一条边及这条边所对的角分别相等的两个三角形称为“关联三角形”.例如,下图中的两个三角形是“关联三角形”.
已知:在Rt△ABC中,∠C=90°,∠A=30°,BC=2,AB=4.
(1)下列三角形中,Rt△ABC的“关联三角形”是________(填序号);
(2)若Rt△ABC的“关联三角形”是等腰三角形,则等腰三角形的底边长可以是 ;
(3)若△DEF是Rt△ABC的“关联三角形”,且△DEF的面积是S, 直接写出S的最大值.
参考答案
一、选择题:(共8个小题,每小题2分,共16分)
ABAB DCDB
二、填空题:(共8个小题,每小题2分,共16分)
9. 4 10. x≥9 11.60° 12.2
13. 14.边角边 15.2 16.①②④
三、解答题
17. (本小题满分8分)
(1)
.
(2)
=72+
=7.
(本小题满分8分)
(1)解:方程两边同时乘以,得,
.
.
.
.
.
检验:当时,方程左右两边相等.
所以原分式方程的解为.
(2)解:方程两边同时乘以(x+2)(x2),得
x2+4x=2(x+2).
x2+4x=2x+4.
3x=6.
x=2.
检验:当x=2时,最简公分母(x+2)(x2)=0,原方程中的分式无意义.
所以原方程无解.
19. (本小题满分5分)
(1)证明:∵AF=CE,
∴AE+EF=CF+EF.
∴AE=CF.
∵BE⊥AC于点E,DF⊥AC于点F,
∴∠AEB =∠CFD=90°.
∴△ABE与△CDF是直角三角形.
在Rt△ABE和Rt△CDF中,
∴Rt△ABE≌Rt△CDF(HL) .
(2)证明:∵Rt△ABE≌Rt△CDF,
∴∠A=∠C.
∴AB∥CD.
20. (本小题满分5分)
甲同学的方法:
证明:如图,作∠BAC的平分线交BC于点D.
∴∠BAD=∠CAD.
在△ABD和△ACD中,
∴△ABD≌△ACD(SAS).
∴∠B=∠C.
乙同学的方法:
证明:如图,作AE⊥BC于点E.
∴∠AEB=∠AEC=90°,
在Rt△ABE和Rt△ACE中,
∴Rt△ABE≌Rt△ACE(HL).
∴∠B=∠C.
丙同学的方法:
证明:如图,取BC的中点F,连接AF.
∴BF=CF.
在△ABF和△ACF中,
∴△ABF≌△ACF(SSS).
∴∠B=∠C.
21. (本小题满分5分)
解:原式=
=
=
=
=.
当a=+2时,原式=.
22. (本小题满分5分)
(1)略;
(2)略;
(3)
23. (本小题满分5分)
(1)如图;
(2)△ADE是等边三角形.
证明:∵△ABC是等边三角形,
∴∠A =∠B=∠C=60°.
∵DE∥BC,
∴∠ADE =∠B=60°,
∠AED =∠C=60°.
∴∠A =∠ADE =∠AED.
∴△ADE是等边三角形.
24. (本小题满分5分)
(1)错误;
(2)条件:∠ODF=∠OEF.
证明:∵OC是∠AOB的角平分线,
∴∠DOF=∠EOF.
在△OFD和△OFE中,
∴△OFD≌△OFE(AAS).
说明:添加的条件可以是①,②,③,⑤,⑥.
25. (本小题满分5分)
解:设自行车的速度为x千米/时,则汽车的速度为3x千米/时,由题意得:
,
解得:x=16,
经检验,x=16是原方程的解,且符合题意.
答:自行车的速度为16千米/时.
26. (本小题满分5分)
(1)如图;
(2)①等边对等角;
②内错角相等,两条直线平行;
(3)略.
27. (本小题满分7分)
(1)如图;
(2)数量关系:∠ECH=∠EGF;
证明:∵GE⊥CE于点E,
∴∠GEF =∠CEH=90°.
∴∠ECH+∠GHD=90°.
∵AD是△ABC的高,
∴∠ADB=90°.
∴∠EGF+∠GHD=90°.
∴∠ECH =∠EGF.
(3)证明:连接DE.
∵∠BAC=90°,AB=AC,
∴∠B=∠ACB=45°.
∵AD是△ABC的高,
∴∠DAC=∠DAB=45°.
∴∠B =∠DAB.
∴DA =DB.
∵点E是AB的中点,
∴∠AED=90°,∠ADE=∠BDE=45°.
∴∠ADE =∠EAD.
∴EA=ED.
∵∠GEF=∠AED=90°,
∴∠AEG =∠DEC.
在△EDC与△EAG中,
∴△EDC≌△EAG(AAS).
∴EC=EG.
28. (本小题满分5分)
(1)①③;
(2)2,4,;
(3).
2
同课章节目录
