北京市门头沟区2024-2025学年八年级上学期期末考试数学试卷(含答案)
文档属性
| 名称 | 北京市门头沟区2024-2025学年八年级上学期期末考试数学试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 14.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-11 19:15:04 | ||
图片预览




文档简介
北京市门头沟区2024-2025学年八年级上学期期末考试
数 学
2025.1
考 生 须 知 1.本试卷共8页,共三道大题,28道小题,满分100分。考试时间120分钟。 2.在试卷和答题卡上准确填写学校名称、姓名、班级和考场。 3.试题答案一律填涂或书写在答题卡上,在试卷上作答无效。 4.答题卡上,选择题、作图题用2B铅笔作答,其他试题用黑色字迹签字笔作答。 5.考试结束,将本试卷、答题卡和草稿纸一并交回。
一、选择题(本题共16分,每小题2分)
第1- 8题均有四个选项,符合题意的选项只有一个.
1.下列是2024年巴黎奥运会运动项目的图标,其中是轴对称图形的是
A B C D
2.某公司运用5G技术,下载一个2.4M的文件大约需要0.000 048秒,将数字0.000 048用
科学记数法表示为
A. B. C. D.
3.如图,AC,BD交于点O,且AO=CO,添加下列条件不能判定△ABO ≌△CDO的是
A.AB=CD B.BO=DO C.∠A=∠C D.∠B=∠D
4.下列计算正确的是
A. B. C. D.
5.如果等腰三角形的三边长分别是x,2,6,那么x的值是
A.2 B.6 C.2或6 D.4或8
6.如图,在△ABC中,∠C=90°,∠A=30°,BD是△ABC的角平分线.
如果点D到AB的距离为1,那么AC的长为
A.2 B.2.5 C.3 D.4
7.下列各式从左到右变形正确的是
A. B. C. D.
8.如图,在△ABC中,∠ACB=90°,AC=BC,AD平分∠BAC交BC于点D,延长AC到点E,
使CE=CD,连接BE交AD的延长线于点F.给出下面四个结论:
①AD=BE; ②BE=2BF;
③AB=AC+CD; ④△ABD的面积是△ACD的面积的2倍;
上述结论中,所有正确结论的序号是
A.①② B.①②③ C.①③④ D.①②③④
二、填空题(本题共16分,每小题2分)
9.如果分式有意义,那么x的取值范围是______.
10.分解因式:______.
11.如果一个多边形的内角和等于外角和,那么该多边形的边数是______.
12.当时,代数式的值为______.
13.如图,在△ABC中,DE垂直平分AB,垂足为D,交BC于点E,连接AE.如果AE=AC,∠B=25°,那么∠C的度数是______.
14.如图,在等边△ABC中,AD是BC边上的高线,且AD=6,E是AB的中点,如果点P在AD上运动,那么BP+EP的最小值是______.
15.如图,点B,E,C在同一条直线上,正方形ABCD与正方形GECF的边长分别为a,b,且,那么阴影部分的面积为_________.
第13题图 第14题图 第15题图
如图,在平面直角坐标系xOy中,已知点A(1,0),B(0,3),
如果点C在第一象限内,且△ABC为等腰直角三角形,那么
点C的坐标是_______.
三、解答题(本题共68分,第17~22题每小题5分,第23~26题每小题6分,第27~28题每小题7分)
解答应写出文字说明、证明过程或演算步骤.
17.计算:.
18.计算:.
19.如图,点A,B,C,D在同一条直线上,AE=DF,AC=DB,BE=CF.
求证:∠E=∠F.
20.解分式方程:.
21.老师设计了一个数学“接力游戏”,由学生合作完成分式的计算.如图,老师把题目交给甲同学,他完成一步计算后,再将结果传递给乙同学,依次进行,最后完成计算.规则是每位同学只能看到前一位同学传过来的式子.
老师 甲 乙 丙
根据上面同学的接力过程,回答以下问题:(1)在“接力游戏”中,从____同学开始出现计算错误,错误的原因是_______________;
(2)请写出正确解答过程.
22.下面是小明设计的尺规作图过程:
已知:如图,△ABC.
求作:∠CDA,使点D在BC上,且∠CDA=2∠ABC.
作法:①分别以点A和点B为圆心,大于AB的长为半径作弧,两弧相交于M,N两点;
②作直线MN,交BC于点D;
③连接AD.
所以∠CDA为所求.
根据小明设计的尺规作图过程,回答以下问题:
(1)使用直尺和圆规,补全图形(保留作图痕迹);
(2)完成下面的证明:
证明:连接AM,BM,AN,BN.
∵AM=BM,AN=BN,
∴点M,N均在线段AB的垂直平分线上.
即:直线MN是线段AB的垂直平分线.
∵点D在直线MN上,
∴AD=_____(_______________________________________)(填推理的依据).
∴∠DAB=∠ABC (__________________________________)(填推理的依据).
∵∠CDA=∠DAB +∠ABC,
∴∠CDA=2∠ABC.
23.先化简,再求值:,其中.
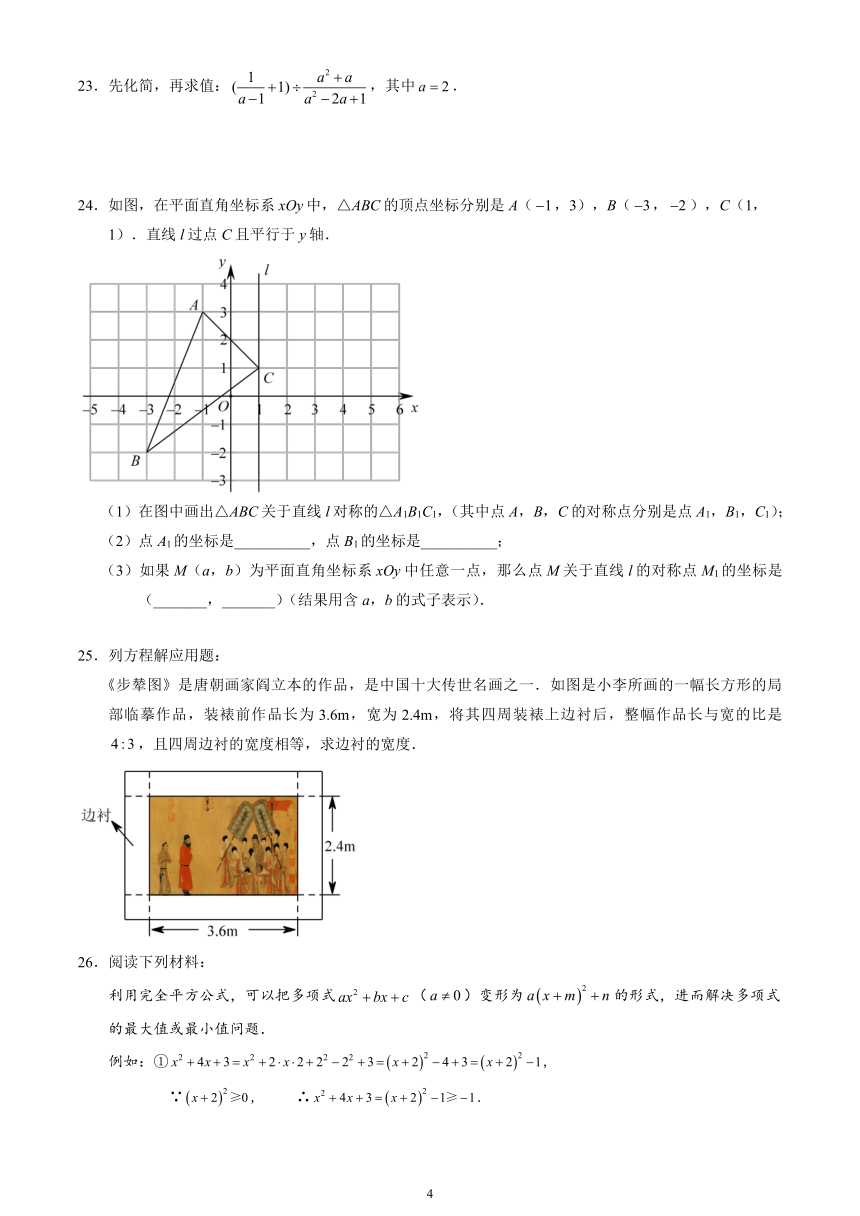
24.如图,在平面直角坐标系xOy中,△ABC的顶点坐标分别是A(,3),B(,),C(1,1).直线l过点C且平行于y轴.
(1)在图中画出△ABC关于直线l对称的△A1B1C1,(其中点A,B,C的对称点分别是点A1,B1,C1);
(2)点A1的坐标是__________,点B1的坐标是__________;
(3)如果M(a,b)为平面直角坐标系xOy中任意一点,那么点M关于直线l的对称点M1的坐标是(_______,_______)(结果用含a,b的式子表示).
25.列方程解应用题:
《步辇图》是唐朝画家阎立本的作品,是中国十大传世名画之一.如图是小李所画的一幅长方形的局部临摹作品,装裱前作品长为3.6m,宽为2.4m,将其四周装裱上边衬后,整幅作品长与宽的比是,且四周边衬的宽度相等,求边衬的宽度.
26.阅读下列材料:
利用完全平方公式,可以把多项式()变形为的形式,进而解决多项式的最大值或最小值问题.
例如:①,
∵, ∴.
∴当时,多项式的最小值为;
②,
∵, ∴.
∴当时,多项式的最大值为.
根据上述材料解决下列问题:
(1)求多项式的最小值,并求出相应的x的值;
(2)如果多项式的最小值是,那么p的值为________;
(3)如图,某学校打算用20米长的篱笆围成一个长方形的花坛,
如果设花坛的一边AB = x米,那么当x =________时,该花
坛的面积最大,最大面积是________平方米.
27.如图,△ABC为等边三角形,点D在AC上,且∠ABD=α(),作点C关于直线BD的对称点E,射线EA交直线BD于点F,连接BE.
(1)依题意补全图形;
(2)求∠EFB的大小;
(3)用等式表示线段AF,BF,EF之间的数量关系,并证明.
28.在平面直角坐标系xOy中,点A与点B关于x轴对称.对于点A和点B,如果存在点P,使PB⊥AB且PB=AB,那么称点P为点A关于点B的“x轴垂半点”.
(1)如图1,点A(1,1),在P1(0,),P2(2,1),P3(,1),P4(2,)中,点A关于点B的“x轴垂半点”是________;
(2)如果点Q(,3)是点E关于点F的“x轴垂半点”,那么点E的坐标是________;
(3)已知点M(2,1),N(0,4),点A是线段MN上任意一点,如果点G是点A关于点B的“x轴垂半点”,那么点G的横坐标t的取值范围是________.
图1 备用图
参考答案
一、选择题(本题共16分,每小题2分)
题号 1 2 3 4 5 6 7 8
答案 D C A D B C A B
二、填空题(本题共16分,每小题2分)
题号 9 10 11 12 13 14 15 16
答案 4 1 6 5
三、解答题(本题共68分,第17~22题每小题5分,第23~26题每小题6分,第27~28题每小题7分)
17.(本小题满分5分)
解:原式 …………………………………………………………………………………………4分
. ………………………………………………………………………………………………5分
18.(本小题满分5分)
解:原式. ………………………………………………………………………………………5分
19.(本小题满分5分)
证明:∵AC=DB ,
∴AC-BC=DB-BC,
即:AB=DC. …………………………………………………………………………………………1分
在△ABE和△DCF中
∴△ABE≌△DCF.…………………………………………………………………………………4分
∴∠E=∠F.……………………………………………………………………………………………5分
20.(本小题满分5分)
解:
……………………………………………………………………1分
………………………………………………………………………2分
……………………………………………………………………………………3分
.…………………………………………………………………………4分
检验:当时,,
∴是原方程的解.
∴原方程的解是. ………………………………………………………………………………5分
21.(本小题满分5分)
解:(1)甲,略; ………………………………………………………………………………………………2分
(2)
………………………………………………………………………3分
…………………………………………………………………………………………4分
.………………………………………………………………………………………………5分
22.(本小题满分5分)
解:(1)略;………………………………………………………………………………………………2分
(2)略.………………………………………………………………………………………………5分
23.(本小题满分6分)
解:
………………………………………………………………………………1分
………………………………………………………………………………………2分
…………………………………………………………………………………………3分
. ……………………………………………………………………………………………4分
当时,
原式. ………………………………………………………………………………6分
24.(本小题满分6分)
解:(1)略;……………………………………………………………………………………………………2分
(2)(,3),(5,); ………………………………………………………………………………4分
(3),b. ……………………………………………………………………………………………6分
25.(本小题满分6分)
解:设边衬的宽度为x m. ……………………………………………………………………………………1分
依题意,得.……………………………………………………………………………… 3分
解得: .……………………………………………………………………………………4分
经检验,是原方程的解,且符合题意. ………………………………………………… 5分
答:边衬的宽度为0.6m.…………………………………………………………………………………6分
26.(本小题满分6分)
解:(1),
∵,
∴.
∴当时,代数式的最小值为;……………………………………………………2分
(2); …………………………………………………………………………………………………4分
(3)5,25. ………………………………………………………………………………………………6分
27.(本小题满分7分)
解:(1)补全图形;……………………………………………………………………………………………1分
(2)∵△ABC为等边三角形,
∴BA=BC=AC,
∠ABC=∠BAC=∠ACB=60°.……………………………2分
∵∠ABD=α,
∴∠CBD=60°-α.
∵点C关于直线BD的对称点为点E,
∴∠EBD=∠CBD=60°-α,BE=BC.……………………………………………………………3分
∴∠EBA=60°-α-α=60°-2α,BE =BA.
∵BE=BA,
∴∠BAE=∠BEA==60° +α.
∵∠BAE=∠EFB+∠ABD,
∴∠EFB=∠BAE-∠ABD=60°+α-α=60°.……………………………………………………4分
(3)线段AF,BF,EF之间的数量关系是BF= AF+ EF.
证明:如图,延长FE到M,使EM = AF,连接BM.
∵BE=BA,
∴∠BEA=∠BAE.
∵∠BEA+∠BEM =180°,∠BAE+∠BAF =180°,
∴∠BEM =∠BAF.
在△BEM和△BAF中,
∵BE=BA,∠BEM =∠BAF,EM =AF,
∴△BEM ≌△BAF.………………………………………………………………………5分
∴BM= BF.
∵∠EFB=60°,
∴△BMF为等边三角形. …………………………………………………………………6分
∴BM =BF = MF.
∵MF = EF+EM,
∴BF= EF+AF.…………………………………………………………………………7分
28.(本小题满分7分)
解:(1),;……………………………………………………………………………………………2分
(2)(2,),(,);……………………………………………………………………………4分
(3),.……………………………………………………………………………7分
说明:
若考生的解法与给出的解法不同,正确者可参照评分参考相应给分。
2
数 学
2025.1
考 生 须 知 1.本试卷共8页,共三道大题,28道小题,满分100分。考试时间120分钟。 2.在试卷和答题卡上准确填写学校名称、姓名、班级和考场。 3.试题答案一律填涂或书写在答题卡上,在试卷上作答无效。 4.答题卡上,选择题、作图题用2B铅笔作答,其他试题用黑色字迹签字笔作答。 5.考试结束,将本试卷、答题卡和草稿纸一并交回。
一、选择题(本题共16分,每小题2分)
第1- 8题均有四个选项,符合题意的选项只有一个.
1.下列是2024年巴黎奥运会运动项目的图标,其中是轴对称图形的是
A B C D
2.某公司运用5G技术,下载一个2.4M的文件大约需要0.000 048秒,将数字0.000 048用
科学记数法表示为
A. B. C. D.
3.如图,AC,BD交于点O,且AO=CO,添加下列条件不能判定△ABO ≌△CDO的是
A.AB=CD B.BO=DO C.∠A=∠C D.∠B=∠D
4.下列计算正确的是
A. B. C. D.
5.如果等腰三角形的三边长分别是x,2,6,那么x的值是
A.2 B.6 C.2或6 D.4或8
6.如图,在△ABC中,∠C=90°,∠A=30°,BD是△ABC的角平分线.
如果点D到AB的距离为1,那么AC的长为
A.2 B.2.5 C.3 D.4
7.下列各式从左到右变形正确的是
A. B. C. D.
8.如图,在△ABC中,∠ACB=90°,AC=BC,AD平分∠BAC交BC于点D,延长AC到点E,
使CE=CD,连接BE交AD的延长线于点F.给出下面四个结论:
①AD=BE; ②BE=2BF;
③AB=AC+CD; ④△ABD的面积是△ACD的面积的2倍;
上述结论中,所有正确结论的序号是
A.①② B.①②③ C.①③④ D.①②③④
二、填空题(本题共16分,每小题2分)
9.如果分式有意义,那么x的取值范围是______.
10.分解因式:______.
11.如果一个多边形的内角和等于外角和,那么该多边形的边数是______.
12.当时,代数式的值为______.
13.如图,在△ABC中,DE垂直平分AB,垂足为D,交BC于点E,连接AE.如果AE=AC,∠B=25°,那么∠C的度数是______.
14.如图,在等边△ABC中,AD是BC边上的高线,且AD=6,E是AB的中点,如果点P在AD上运动,那么BP+EP的最小值是______.
15.如图,点B,E,C在同一条直线上,正方形ABCD与正方形GECF的边长分别为a,b,且,那么阴影部分的面积为_________.
第13题图 第14题图 第15题图
如图,在平面直角坐标系xOy中,已知点A(1,0),B(0,3),
如果点C在第一象限内,且△ABC为等腰直角三角形,那么
点C的坐标是_______.
三、解答题(本题共68分,第17~22题每小题5分,第23~26题每小题6分,第27~28题每小题7分)
解答应写出文字说明、证明过程或演算步骤.
17.计算:.
18.计算:.
19.如图,点A,B,C,D在同一条直线上,AE=DF,AC=DB,BE=CF.
求证:∠E=∠F.
20.解分式方程:.
21.老师设计了一个数学“接力游戏”,由学生合作完成分式的计算.如图,老师把题目交给甲同学,他完成一步计算后,再将结果传递给乙同学,依次进行,最后完成计算.规则是每位同学只能看到前一位同学传过来的式子.
老师 甲 乙 丙
根据上面同学的接力过程,回答以下问题:(1)在“接力游戏”中,从____同学开始出现计算错误,错误的原因是_______________;
(2)请写出正确解答过程.
22.下面是小明设计的尺规作图过程:
已知:如图,△ABC.
求作:∠CDA,使点D在BC上,且∠CDA=2∠ABC.
作法:①分别以点A和点B为圆心,大于AB的长为半径作弧,两弧相交于M,N两点;
②作直线MN,交BC于点D;
③连接AD.
所以∠CDA为所求.
根据小明设计的尺规作图过程,回答以下问题:
(1)使用直尺和圆规,补全图形(保留作图痕迹);
(2)完成下面的证明:
证明:连接AM,BM,AN,BN.
∵AM=BM,AN=BN,
∴点M,N均在线段AB的垂直平分线上.
即:直线MN是线段AB的垂直平分线.
∵点D在直线MN上,
∴AD=_____(_______________________________________)(填推理的依据).
∴∠DAB=∠ABC (__________________________________)(填推理的依据).
∵∠CDA=∠DAB +∠ABC,
∴∠CDA=2∠ABC.
23.先化简,再求值:,其中.
24.如图,在平面直角坐标系xOy中,△ABC的顶点坐标分别是A(,3),B(,),C(1,1).直线l过点C且平行于y轴.
(1)在图中画出△ABC关于直线l对称的△A1B1C1,(其中点A,B,C的对称点分别是点A1,B1,C1);
(2)点A1的坐标是__________,点B1的坐标是__________;
(3)如果M(a,b)为平面直角坐标系xOy中任意一点,那么点M关于直线l的对称点M1的坐标是(_______,_______)(结果用含a,b的式子表示).
25.列方程解应用题:
《步辇图》是唐朝画家阎立本的作品,是中国十大传世名画之一.如图是小李所画的一幅长方形的局部临摹作品,装裱前作品长为3.6m,宽为2.4m,将其四周装裱上边衬后,整幅作品长与宽的比是,且四周边衬的宽度相等,求边衬的宽度.
26.阅读下列材料:
利用完全平方公式,可以把多项式()变形为的形式,进而解决多项式的最大值或最小值问题.
例如:①,
∵, ∴.
∴当时,多项式的最小值为;
②,
∵, ∴.
∴当时,多项式的最大值为.
根据上述材料解决下列问题:
(1)求多项式的最小值,并求出相应的x的值;
(2)如果多项式的最小值是,那么p的值为________;
(3)如图,某学校打算用20米长的篱笆围成一个长方形的花坛,
如果设花坛的一边AB = x米,那么当x =________时,该花
坛的面积最大,最大面积是________平方米.
27.如图,△ABC为等边三角形,点D在AC上,且∠ABD=α(),作点C关于直线BD的对称点E,射线EA交直线BD于点F,连接BE.
(1)依题意补全图形;
(2)求∠EFB的大小;
(3)用等式表示线段AF,BF,EF之间的数量关系,并证明.
28.在平面直角坐标系xOy中,点A与点B关于x轴对称.对于点A和点B,如果存在点P,使PB⊥AB且PB=AB,那么称点P为点A关于点B的“x轴垂半点”.
(1)如图1,点A(1,1),在P1(0,),P2(2,1),P3(,1),P4(2,)中,点A关于点B的“x轴垂半点”是________;
(2)如果点Q(,3)是点E关于点F的“x轴垂半点”,那么点E的坐标是________;
(3)已知点M(2,1),N(0,4),点A是线段MN上任意一点,如果点G是点A关于点B的“x轴垂半点”,那么点G的横坐标t的取值范围是________.
图1 备用图
参考答案
一、选择题(本题共16分,每小题2分)
题号 1 2 3 4 5 6 7 8
答案 D C A D B C A B
二、填空题(本题共16分,每小题2分)
题号 9 10 11 12 13 14 15 16
答案 4 1 6 5
三、解答题(本题共68分,第17~22题每小题5分,第23~26题每小题6分,第27~28题每小题7分)
17.(本小题满分5分)
解:原式 …………………………………………………………………………………………4分
. ………………………………………………………………………………………………5分
18.(本小题满分5分)
解:原式. ………………………………………………………………………………………5分
19.(本小题满分5分)
证明:∵AC=DB ,
∴AC-BC=DB-BC,
即:AB=DC. …………………………………………………………………………………………1分
在△ABE和△DCF中
∴△ABE≌△DCF.…………………………………………………………………………………4分
∴∠E=∠F.……………………………………………………………………………………………5分
20.(本小题满分5分)
解:
……………………………………………………………………1分
………………………………………………………………………2分
……………………………………………………………………………………3分
.…………………………………………………………………………4分
检验:当时,,
∴是原方程的解.
∴原方程的解是. ………………………………………………………………………………5分
21.(本小题满分5分)
解:(1)甲,略; ………………………………………………………………………………………………2分
(2)
………………………………………………………………………3分
…………………………………………………………………………………………4分
.………………………………………………………………………………………………5分
22.(本小题满分5分)
解:(1)略;………………………………………………………………………………………………2分
(2)略.………………………………………………………………………………………………5分
23.(本小题满分6分)
解:
………………………………………………………………………………1分
………………………………………………………………………………………2分
…………………………………………………………………………………………3分
. ……………………………………………………………………………………………4分
当时,
原式. ………………………………………………………………………………6分
24.(本小题满分6分)
解:(1)略;……………………………………………………………………………………………………2分
(2)(,3),(5,); ………………………………………………………………………………4分
(3),b. ……………………………………………………………………………………………6分
25.(本小题满分6分)
解:设边衬的宽度为x m. ……………………………………………………………………………………1分
依题意,得.……………………………………………………………………………… 3分
解得: .……………………………………………………………………………………4分
经检验,是原方程的解,且符合题意. ………………………………………………… 5分
答:边衬的宽度为0.6m.…………………………………………………………………………………6分
26.(本小题满分6分)
解:(1),
∵,
∴.
∴当时,代数式的最小值为;……………………………………………………2分
(2); …………………………………………………………………………………………………4分
(3)5,25. ………………………………………………………………………………………………6分
27.(本小题满分7分)
解:(1)补全图形;……………………………………………………………………………………………1分
(2)∵△ABC为等边三角形,
∴BA=BC=AC,
∠ABC=∠BAC=∠ACB=60°.……………………………2分
∵∠ABD=α,
∴∠CBD=60°-α.
∵点C关于直线BD的对称点为点E,
∴∠EBD=∠CBD=60°-α,BE=BC.……………………………………………………………3分
∴∠EBA=60°-α-α=60°-2α,BE =BA.
∵BE=BA,
∴∠BAE=∠BEA==60° +α.
∵∠BAE=∠EFB+∠ABD,
∴∠EFB=∠BAE-∠ABD=60°+α-α=60°.……………………………………………………4分
(3)线段AF,BF,EF之间的数量关系是BF= AF+ EF.
证明:如图,延长FE到M,使EM = AF,连接BM.
∵BE=BA,
∴∠BEA=∠BAE.
∵∠BEA+∠BEM =180°,∠BAE+∠BAF =180°,
∴∠BEM =∠BAF.
在△BEM和△BAF中,
∵BE=BA,∠BEM =∠BAF,EM =AF,
∴△BEM ≌△BAF.………………………………………………………………………5分
∴BM= BF.
∵∠EFB=60°,
∴△BMF为等边三角形. …………………………………………………………………6分
∴BM =BF = MF.
∵MF = EF+EM,
∴BF= EF+AF.…………………………………………………………………………7分
28.(本小题满分7分)
解:(1),;……………………………………………………………………………………………2分
(2)(2,),(,);……………………………………………………………………………4分
(3),.……………………………………………………………………………7分
说明:
若考生的解法与给出的解法不同,正确者可参照评分参考相应给分。
2
同课章节目录
