人教版数学八年级上学期期末综合练习(含答案)
文档属性
| 名称 | 人教版数学八年级上学期期末综合练习(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 694.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-12 00:00:00 | ||
图片预览




文档简介
人教版数学八年级上学期期末综合练习
学校:___________姓名:___________班级:___________学号:___________
一、单选题
1.年巴黎奥运会和残奥会体育图标一共个.与近年来各大体育类赛事图标都注重运动员运动状态刻画不同,巴黎奥运会则是注重项目本身的展现.此次巴黎奥运会项目图标在视觉设计上主要融入三个方面的元素——对称轴设计、项目场地的抽象表达以及项目的代表性元素.如图,下列哪个图标属于轴对称图形(忽略图标上的文字标注)( )
A.射箭项目图标 B.跳水项目图标
C.铁人三项图标 D.赛跑项目图标
2.下列计算正确的是( )
A. B.
C. D.
3.如图,为了估计池塘两岸、间的距离,在池塘的一侧选取点,测得米,米,那么、间的距离不可能是( )
A.6米 B.8.8米 C.17米 D.26米
4.下列多项式乘法中,能用平方差公式计算的是( )
A. B.
C. D.
5.如图,,若,则的度数为( )
A. B. C. D.
6.如图,C,E是直线l两侧的点,以点C为圆心,的长为半径画弧交直线l于A,B两点,再分别以点A,B为圆心,大于的长为半径画弧,两弧交于点D,连接,则下列结论不一定正确的是( )
A. B.直线l
C.是直角三角形 D.点A,B关于直线对称
7.如图,是中的平分线,是的外角的平分线,如果,,则( )
A. B. C. D.
8.若关于x的方程 的解为正数,则m的取值范围是( )
A. B. C. 且 D. 且
9.如图是学习分式方程应用时,老师板书的问题和两名同学所列的方程.
15.3分式方程 例:有甲、乙两个工程队,甲队修路400米与乙队修路600米所用时间相等,乙队每天比甲队多修20米,求甲队每天修路的长度. 冰冰: 庆庆:
方程中的x和y表示的意义,下列说法错误的是( )
A.x表示甲队每天修路的长度 B.x表示乙队每天修路的长度
C.y表示甲队修400米所用的时间 D.y表示乙队修600米所用的时间
10.如图,是的角平分线,,垂足为,交的延长线于点,若恰好平分,.给出下列四个结论:①;②;③;④.其中正确的结论共有( )
A.4个 B.3个 C.2个 D.1个
二、填空题
11.将多项式配成完全平方式: .
12.在直角坐标系中,若点与点关于y轴对称,则 .
13.如图,中,,,,与的平分线相交于点,过点作,则的周长为 .
14.已知:,则x2+5xy+y2= .
15.如图,在中,AB=AC,AB的垂直平分线交AB于点D,交AC于点E,且与的周长分别是16和10,则AB的长为
16.若关于x的方程无解,则a的值是 .
17.如图,在中,点是边上的一点,,,将沿折叠得到,与交于点.则的度数是 .
18.如图,已知点P是角平分线上的一点,,如果点C是上一个动点.
(1)若时,与的位置关系 ;
(2)最小值为 .
三、解答题
19.(1)计算:;
(2)计算:;
(3)因式分解:;
(4)解分式方程:.
20.先化简:再从,1,2中选取一个合适的数作为的值代入求值.
21.如图,在网格图中建立平面直角坐标系,的三个顶点坐标分别为,,.
(1)若与关于轴对称,点A,B,C的对应点分别为,,,则各顶点的坐标分别为__________,__________,__________.
(2)请在网格上画出关于轴的对称图形,点A,B,C的对应点分别为,,.
(3)求的面积.
22.如图所示,在和中给出4个论断:①;②;③;④,;现将4个论断分别粘贴在四个学生的后背上,进行如下游戏:其中三个学生站在讲台的左边,另一个学生站在讲台的右边,要求以三个学生后背上的部分论断作为题设,另一个学生后背上的论断作为结论,使之成为一个真命题或题目,这个游戏可进行几轮?并对其中的一种情况进行证明.
23.恰逢2024甲辰龙年,家家户户都挂上龙元素的饰品,某校初2025届学生也在“衍纸画龙庆新春,巧手实践迎新年”的实践活动中,创造了许多美丽、独特的“龙年装饰画”,其中有19幅作品获得一等奖.某文创店老板抓住商机花费4000元采购了一批“龙年装饰画”,并全部售完,于是该老板又第二次采购,但第二次采购时每件的进价贵了5元,采购费用为18000元,且采购数量是第一次采购的4倍.
(1)该老板采购第一批、第二批“龙年装饰画”时,每件的进价分别是多少元?
(2)该老板两批“龙年装饰画”按相同的标价售出,但是最后的50件“龙年装饰画”按八折优惠售出,老板在销售过程中额外的成本为1000元,该老板要使两批“龙年装饰画”全部售完后利润不低于6400元,那么每件“龙年装饰画”的标价至少是多少元?
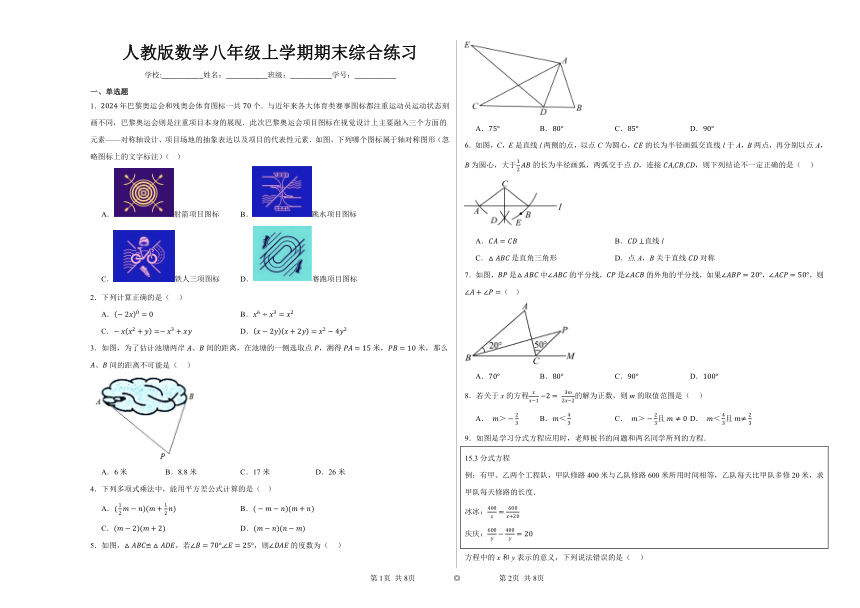
24.如图①是一个长为,宽为的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后按图②的形状拼成一个正方形.
(1)图②中的阴影部分的面积为__________;
(2)观察图②,三个代数式,之间的等量关系是___________.
(3)若,求的值.
(4)观察图③,你能得到怎样的等式呢?
(5)试画出一个几何图形,使它的面积能表示.
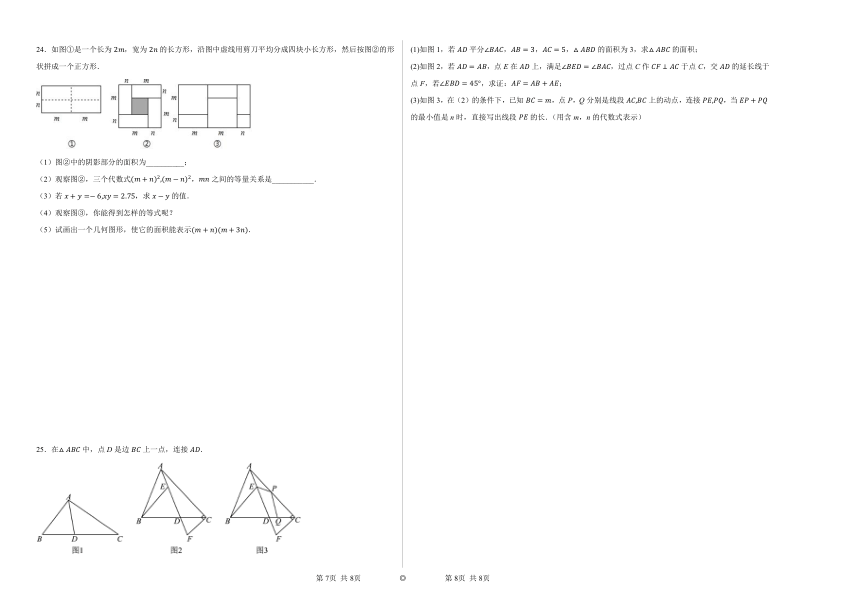
25.在中,点D是边上一点,连接.
(1)如图1,若平分,,,的面积为3,求的面积;
(2)如图2,若,点E在上,满足,过点C作于点C,交的延长线于点F,若,求证:;
(3)如图3,在(2)的条件下,已知,点P,Q分别是线段上的动点,连接,当的最小值是n时,直接写出线段的长.(用含m,n的代数式表示)
第1页 共4页 ◎ 第2页 共4页
第1页 共4页 ◎ 第2页 共4页
参考答案
1.A
2.D
3.D
4.C
5.C
6.C
7.C
8.D
9.B
10.B
11.16
12.-2
13.
14.32
15.6
16.1或2
17.
18. 4
19.解:(1)
;
(2)
;
(3)
;
(4),
方程两边都乘,得,
,
,
,
检验:当时,,
所以分式方程的解是.
20.解:原式
,
,,
,,
取,
当时,
原式.
21.(1)解:∵与关于轴对称,的顶点坐标分别为,,,
∴各顶点的坐标分别为 , ,
(2)解:如图所示,即为所求,
(3)解:的面积为
22.可进行3轮;②③④→①;①②④→③;①③④→②.
对于命题②③④→①:
已知,,,.求证:.
证明:∵,∴,
在和中,
∴,
∴.
23.(1)设该老板采购第一批“龙年装饰画”时每件的进价是x元,则该老板采购第二批“龙年装饰画”时每件的进价是元,
根据题意得:,
解得:,
经检验,是所列方程的解,且符合题意,
∴(元).
答:该老板采购第一批“龙年装饰画”时每件的进价是40元,采购第二批“龙年装饰画”时每件的进价是45元;
(2)该老板采购第一批“龙年装饰画”的数量是(件),
该老板采购第二批“龙年装饰画”的数量是(件).
设每件“龙年装饰画”的标价是y元,
根据题意得:,
解得:,
∴y的最小值为60.
答:每件“龙年装饰画”的标价至少是60元.
24.解:(1)图②中阴影部分为边长为(m-n)的正方形,其面积为:(m-n)2
(2)最外层大正方形的面积为:(m+n)2,4个长方形的面积为4mn,
阴影部分面积为(m-n)2,总体看图形的面积和分部分之和的面积相等
(m+n)2-4mn=(m-n)2.
(3)∵,
∴(x-y)2=(x+y)2-4xy=36-11=25
∴x-y=±5
(4)由整体求面积和分部分求面积,二者相等,可得:
(2m+n)(m+n)=2m2+3mn+n2.
(5)
25.(1)解:过点D作于点G,于点H,如图所示:
∵,
∴,即
∴
∵平分
∴
∴
∴;
(2)过点D作,交于点N,如图所示:
∴,
∵,即
∴
在和中
∴
∴
∵,
∴
即
∴
∵
∴
∴
∴
∵
∴
在和中
∴
∴
∴
又∵,
∴;
(3),理由如下:
由(2)可知
延长交于点K,则
再倍长至点,过点作于点Q,交于点P
由轴对称性得
∴最小,即
在中,
∴
又在中,
∴.
学校:___________姓名:___________班级:___________学号:___________
一、单选题
1.年巴黎奥运会和残奥会体育图标一共个.与近年来各大体育类赛事图标都注重运动员运动状态刻画不同,巴黎奥运会则是注重项目本身的展现.此次巴黎奥运会项目图标在视觉设计上主要融入三个方面的元素——对称轴设计、项目场地的抽象表达以及项目的代表性元素.如图,下列哪个图标属于轴对称图形(忽略图标上的文字标注)( )
A.射箭项目图标 B.跳水项目图标
C.铁人三项图标 D.赛跑项目图标
2.下列计算正确的是( )
A. B.
C. D.
3.如图,为了估计池塘两岸、间的距离,在池塘的一侧选取点,测得米,米,那么、间的距离不可能是( )
A.6米 B.8.8米 C.17米 D.26米
4.下列多项式乘法中,能用平方差公式计算的是( )
A. B.
C. D.
5.如图,,若,则的度数为( )
A. B. C. D.
6.如图,C,E是直线l两侧的点,以点C为圆心,的长为半径画弧交直线l于A,B两点,再分别以点A,B为圆心,大于的长为半径画弧,两弧交于点D,连接,则下列结论不一定正确的是( )
A. B.直线l
C.是直角三角形 D.点A,B关于直线对称
7.如图,是中的平分线,是的外角的平分线,如果,,则( )
A. B. C. D.
8.若关于x的方程 的解为正数,则m的取值范围是( )
A. B. C. 且 D. 且
9.如图是学习分式方程应用时,老师板书的问题和两名同学所列的方程.
15.3分式方程 例:有甲、乙两个工程队,甲队修路400米与乙队修路600米所用时间相等,乙队每天比甲队多修20米,求甲队每天修路的长度. 冰冰: 庆庆:
方程中的x和y表示的意义,下列说法错误的是( )
A.x表示甲队每天修路的长度 B.x表示乙队每天修路的长度
C.y表示甲队修400米所用的时间 D.y表示乙队修600米所用的时间
10.如图,是的角平分线,,垂足为,交的延长线于点,若恰好平分,.给出下列四个结论:①;②;③;④.其中正确的结论共有( )
A.4个 B.3个 C.2个 D.1个
二、填空题
11.将多项式配成完全平方式: .
12.在直角坐标系中,若点与点关于y轴对称,则 .
13.如图,中,,,,与的平分线相交于点,过点作,则的周长为 .
14.已知:,则x2+5xy+y2= .
15.如图,在中,AB=AC,AB的垂直平分线交AB于点D,交AC于点E,且与的周长分别是16和10,则AB的长为
16.若关于x的方程无解,则a的值是 .
17.如图,在中,点是边上的一点,,,将沿折叠得到,与交于点.则的度数是 .
18.如图,已知点P是角平分线上的一点,,如果点C是上一个动点.
(1)若时,与的位置关系 ;
(2)最小值为 .
三、解答题
19.(1)计算:;
(2)计算:;
(3)因式分解:;
(4)解分式方程:.
20.先化简:再从,1,2中选取一个合适的数作为的值代入求值.
21.如图,在网格图中建立平面直角坐标系,的三个顶点坐标分别为,,.
(1)若与关于轴对称,点A,B,C的对应点分别为,,,则各顶点的坐标分别为__________,__________,__________.
(2)请在网格上画出关于轴的对称图形,点A,B,C的对应点分别为,,.
(3)求的面积.
22.如图所示,在和中给出4个论断:①;②;③;④,;现将4个论断分别粘贴在四个学生的后背上,进行如下游戏:其中三个学生站在讲台的左边,另一个学生站在讲台的右边,要求以三个学生后背上的部分论断作为题设,另一个学生后背上的论断作为结论,使之成为一个真命题或题目,这个游戏可进行几轮?并对其中的一种情况进行证明.
23.恰逢2024甲辰龙年,家家户户都挂上龙元素的饰品,某校初2025届学生也在“衍纸画龙庆新春,巧手实践迎新年”的实践活动中,创造了许多美丽、独特的“龙年装饰画”,其中有19幅作品获得一等奖.某文创店老板抓住商机花费4000元采购了一批“龙年装饰画”,并全部售完,于是该老板又第二次采购,但第二次采购时每件的进价贵了5元,采购费用为18000元,且采购数量是第一次采购的4倍.
(1)该老板采购第一批、第二批“龙年装饰画”时,每件的进价分别是多少元?
(2)该老板两批“龙年装饰画”按相同的标价售出,但是最后的50件“龙年装饰画”按八折优惠售出,老板在销售过程中额外的成本为1000元,该老板要使两批“龙年装饰画”全部售完后利润不低于6400元,那么每件“龙年装饰画”的标价至少是多少元?
24.如图①是一个长为,宽为的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后按图②的形状拼成一个正方形.
(1)图②中的阴影部分的面积为__________;
(2)观察图②,三个代数式,之间的等量关系是___________.
(3)若,求的值.
(4)观察图③,你能得到怎样的等式呢?
(5)试画出一个几何图形,使它的面积能表示.
25.在中,点D是边上一点,连接.
(1)如图1,若平分,,,的面积为3,求的面积;
(2)如图2,若,点E在上,满足,过点C作于点C,交的延长线于点F,若,求证:;
(3)如图3,在(2)的条件下,已知,点P,Q分别是线段上的动点,连接,当的最小值是n时,直接写出线段的长.(用含m,n的代数式表示)
第1页 共4页 ◎ 第2页 共4页
第1页 共4页 ◎ 第2页 共4页
参考答案
1.A
2.D
3.D
4.C
5.C
6.C
7.C
8.D
9.B
10.B
11.16
12.-2
13.
14.32
15.6
16.1或2
17.
18. 4
19.解:(1)
;
(2)
;
(3)
;
(4),
方程两边都乘,得,
,
,
,
检验:当时,,
所以分式方程的解是.
20.解:原式
,
,,
,,
取,
当时,
原式.
21.(1)解:∵与关于轴对称,的顶点坐标分别为,,,
∴各顶点的坐标分别为 , ,
(2)解:如图所示,即为所求,
(3)解:的面积为
22.可进行3轮;②③④→①;①②④→③;①③④→②.
对于命题②③④→①:
已知,,,.求证:.
证明:∵,∴,
在和中,
∴,
∴.
23.(1)设该老板采购第一批“龙年装饰画”时每件的进价是x元,则该老板采购第二批“龙年装饰画”时每件的进价是元,
根据题意得:,
解得:,
经检验,是所列方程的解,且符合题意,
∴(元).
答:该老板采购第一批“龙年装饰画”时每件的进价是40元,采购第二批“龙年装饰画”时每件的进价是45元;
(2)该老板采购第一批“龙年装饰画”的数量是(件),
该老板采购第二批“龙年装饰画”的数量是(件).
设每件“龙年装饰画”的标价是y元,
根据题意得:,
解得:,
∴y的最小值为60.
答:每件“龙年装饰画”的标价至少是60元.
24.解:(1)图②中阴影部分为边长为(m-n)的正方形,其面积为:(m-n)2
(2)最外层大正方形的面积为:(m+n)2,4个长方形的面积为4mn,
阴影部分面积为(m-n)2,总体看图形的面积和分部分之和的面积相等
(m+n)2-4mn=(m-n)2.
(3)∵,
∴(x-y)2=(x+y)2-4xy=36-11=25
∴x-y=±5
(4)由整体求面积和分部分求面积,二者相等,可得:
(2m+n)(m+n)=2m2+3mn+n2.
(5)
25.(1)解:过点D作于点G,于点H,如图所示:
∵,
∴,即
∴
∵平分
∴
∴
∴;
(2)过点D作,交于点N,如图所示:
∴,
∵,即
∴
在和中
∴
∴
∵,
∴
即
∴
∵
∴
∴
∴
∵
∴
在和中
∴
∴
∴
又∵,
∴;
(3),理由如下:
由(2)可知
延长交于点K,则
再倍长至点,过点作于点Q,交于点P
由轴对称性得
∴最小,即
在中,
∴
又在中,
∴.
