2024-2025学年期末达标测试卷(含解析)-数学八年级上册北师大版
文档属性
| 名称 | 2024-2025学年期末达标测试卷(含解析)-数学八年级上册北师大版 |  | |
| 格式 | docx | ||
| 文件大小 | 559.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-10 19:47:31 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
2024-2025学年期末达标测试卷-数学八年级上册北师大版
一.选择题(共10小题)
1.(2024秋 凤城市期中)如图是小刚画的一张脸,如果他用(1,3)表示左眼,用(3,3)表示右眼,那么嘴的位置可以表示成( )
A.(2,1) B.(2,2) C.(2,3) D.(1,2)
2.(2024秋 丰城市校级月考)使二次根式有意义的a的取值范围是( )
A.a≠5 B.a>5 C.a≤5 D.a<5
3.(2023秋 阳城县期末)“数轴上的点并不都表示有理数,如图所示,数轴上的点P所表示的数是”,这种说明问题的方式体现的数学思想是( )
A.方程思想 B.建模思想
C.数形结合思想 D.分类讨论思想
4.(2024 凉州区校级一模)如图,∠ACE是△ABC的外角,BD平分∠ABC,CD平分∠ACE,且BD,CD相交于点D.若∠A=80°,则∠D等于( )
A.30° B.40° C.50° D.55°
5.(2023秋 桐城市校级期末)下列命题:①垂直于同一条直线的两条直线平行;②两直线平行,同位角相等;③对顶角相等;④若ax>a,则x>1;⑤邻补角的平分线互相垂直,其中真命题的个数是( )
A.1 B.2 C.3 D.4
6.(2023秋 凤翔区期末)下列运算正确的是( )
A. B. C. D.
7.(2023秋 文昌校级期末)点A(x,y1)在函数y=2x的图象上,点B(x,y2)在y=﹣x+3的图象上,若使y1≥y2则x的取值范围应为( )
A.x≤3 B.x≥3 C.x≤1 D.x≥1
8.(2023秋 未央区校级期末)如表记录了甲、乙、丙、丁四名跳高运动员最近几次选拔赛成绩的平均数与方差:
甲 乙 丙 丁
平均数(cm) 180 185 180 185
方差 8.1 7.4 3.6 3.6
根据表中数据,要从中选择一名成绩好且发挥稳定的运动员参加比赛,应该选择( )
A.甲 B.乙 C.丙 D.丁
9.(2023秋 金台区期末)我国古代问题:以绳测井,若将绳三折测之,绳多四尺,若将绳四折测之,绳多一尺,绳长、井深各几何?这段话的意思是:用绳子量井深,把绳三折来量,井外余绳四尺,把绳四折来量,井外余绳一尺,绳长、井深各几尺?若设绳长为x尺,井深为y尺,则符合题意的方程组是( )
A. B.
C. D.
10.(2024秋 萧山区月考)如图,分别以直角三角形三边为边长作正方形、半圆、正三角形、直角三角形,不存在S1+S2=S3的面积关系的是( )
A. B.
C. D.
二.填空题(共7小题)
11.(2024 包河区二模)命题“如果a,b互为相反数,那么a+b=0”的逆命题为: .
12.(2024秋 贵州期中)的算术平方根是 ,的平方根是 .
13.(2024秋 南海区校级月考)已知点A(6,﹣7),则点A到x轴的距离是 .
14.(2023秋 雁塔区校级期末)若关于x,y的二元一次方程组的解也是x+2y=3的解,则k的值为 .
15.(2023秋 成安县期末)如图,在平面直角坐标系中,直线yx+3交x轴于点A,交y轴于点B,以点A为圆心,AB长为半径画弧,交x轴的负半轴于点C,则直线BC的解析式为 .
16.(2023秋 成都期末)如图,有两棵树,一棵高12米,另一棵高7米,两树相距12米,一只小鸟从一棵树的树梢A飞到另一棵树的树梢B,则小鸟至少要飞行 米.
17.(2023秋 西安区校级期末)如图,在△ABC中,AD平分∠BAC,∠BAC,BE平分∠ABC,AD BE,AD、BE交于点O,OF⊥BC,若∠C=70°,∠BAC=60°,则∠DOF= .
三.解答题(共7小题)
18.(2023秋 未央区校级期末)计算:.
19.(2023秋 七里河区校级期末)解方程组:
(1);
(2).
20.(2023秋 桐城市校级期末)已知一次函数y=(3﹣m)x+2m﹣9的图象与y轴的负半轴相交,y随x的增大而减小,且m为整数.
(1)求m的值.
(2)当﹣1≤x≤2时,求y的取值范围.
21.(2023秋 新城区校级期末)2023年12月4日是我国第10个“国家宪法日”,为推动广大学生树立宪法意识、增强法制观念,11月底,全国青少年普法网举办了全国学生“学宪法讲宪法”活动,某中学为了了解九年级学生的答题情况,随机抽取了部分学生的成绩,并将调查结果绘制成了如图所示的统计图.
所抽取该校九年级学生“学宪法讲宪法”活动测试成绩的统计图:
(1)补全两幅统计图;
(2)本次抽查学生成绩的众数是 ,中位数是 ;
(3)该校九年级学生有1200人,全部参加考试,请估计该校九年级学生在测试中不低于80分的学生有多少人?
22.(2023秋 裕安区校级期末)某礼品店为迎接农历新年的到来,准备购进一批适合学生的礼品.已知购进4件A礼品和12件B礼品共需360元,购进8件A礼品和6件B礼品共需270元.
(1)(列二元一次方程组)求A,B两种礼品每件的进价.
(2)该店计划将5000元全部用于购进A,B这两种礼品,设购进A礼品m件,B礼品n件.
①求n与m之间的关系式;
②该店进货时,厂家要求A礼品的购进数量不少于100件.已知A礼品每件售价为20元,B礼品每件售价为35元.设该店全部售出这两种礼品可获利W元,求W与m之间的关系式和该店所获利润的最大值.
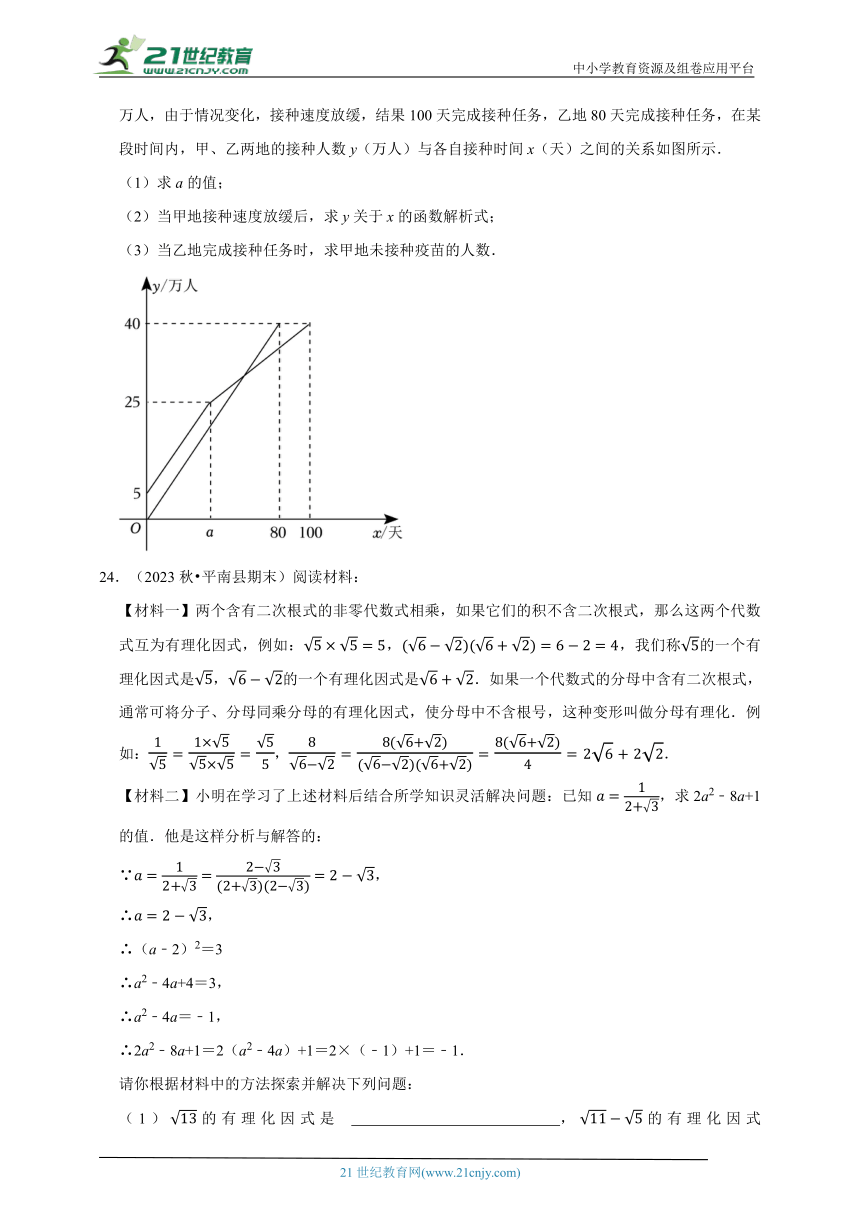
23.(2023秋 成安县期末)疫苗接种,利国利民.甲、乙两地分别对本地各40万人接种新冠疫苗.甲地在前期完成5万人接种后,甲、乙两地同时以相同速度接种,甲地经过a天后接种人数达到25万人,由于情况变化,接种速度放缓,结果100天完成接种任务,乙地80天完成接种任务,在某段时间内,甲、乙两地的接种人数y(万人)与各自接种时间x(天)之间的关系如图所示.
(1)求a的值;
(2)当甲地接种速度放缓后,求y关于x的函数解析式;
(3)当乙地完成接种任务时,求甲地未接种疫苗的人数.
24.(2023秋 平南县期末)阅读材料:
【材料一】两个含有二次根式的非零代数式相乘,如果它们的积不含二次根式,那么这两个代数式互为有理化因式,例如:,,我们称的一个有理化因式是,的一个有理化因式是.如果一个代数式的分母中含有二次根式,通常可将分子、分母同乘分母的有理化因式,使分母中不含根号,这种变形叫做分母有理化.例如:,.
【材料二】小明在学习了上述材料后结合所学知识灵活解决问题:已知,求2a2﹣8a+1的值.他是这样分析与解答的:
∵,
∴,
∴(a﹣2)2=3
∴a2﹣4a+4=3,
∴a2﹣4a=﹣1,
∴2a2﹣8a+1=2(a2﹣4a)+1=2×(﹣1)+1=﹣1.
请你根据材料中的方法探索并解决下列问题:
(1)的有理化因式是 ,的有理化因式是 ;(均写出一个即可)
(2)计算:;
(3)若,求3a2﹣6a+5的值.
2024-2025学年期末达标测试卷-数学八年级上册北师大版
参考答案与试题解析
题号 1 2 3 4 5 6 7 8 9 10
答案 A C C B C D D D D D
一.选择题(共10小题)
1.(2024秋 凤城市期中)如图是小刚画的一张脸,如果他用(1,3)表示左眼,用(3,3)表示右眼,那么嘴的位置可以表示成( )
A.(2,1) B.(2,2) C.(2,3) D.(1,2)
【解答】解:∵用(1,3)表示左眼,用(3,3)表示右眼,
∴坐标系的位置如图:
∴嘴的位置可以表示成(2,1);
故选:A.
2.(2024秋 丰城市校级月考)使二次根式有意义的a的取值范围是( )
A.a≠5 B.a>5 C.a≤5 D.a<5
【解答】解:由题意得:5﹣a≥0,
解得a≤5,
故选:C.
3.(2023秋 阳城县期末)“数轴上的点并不都表示有理数,如图所示,数轴上的点P所表示的数是”,这种说明问题的方式体现的数学思想是( )
A.方程思想 B.建模思想
C.数形结合思想 D.分类讨论思想
【解答】解:∵数轴上的点并不都表示有理数,如图中数轴上的点P所表示的数是,
这种利用图形直观说明问题的方式A、B、D的说法显然不正确,
∴本题是把数与数轴上的点相联系,是数形结合的思想方法.
故选:C.
4.(2024 凉州区校级一模)如图,∠ACE是△ABC的外角,BD平分∠ABC,CD平分∠ACE,且BD,CD相交于点D.若∠A=80°,则∠D等于( )
A.30° B.40° C.50° D.55°
【解答】解:∵BD平分∠ABC,CD平分∠ACE,
∴∠ABC=2∠DBC,∠ACE=2∠DCE.
∴∠DBC=2∠D.
∵∠A=80°,
∴.
故选:B.
5.(2023秋 桐城市校级期末)下列命题:①垂直于同一条直线的两条直线平行;②两直线平行,同位角相等;③对顶角相等;④若ax>a,则x>1;⑤邻补角的平分线互相垂直,其中真命题的个数是( )
A.1 B.2 C.3 D.4
【解答】解:①垂直于同一条直线的两条直线平行是错误的,要强调同一平面内;
②两直线平行,同位角相等;是正确的;
③对顶角相等;是正确的;
④若ax>a,则x>1是错误的;要强调前提是a>0;
⑤邻补角的平分线互相垂直,是正确的;
故选:C.
6.(2023秋 凤翔区期末)下列运算正确的是( )
A. B. C. D.
【解答】解:A、与不能合并,所以A选项错误;
B、原式=3,所以B选项错误;
C、原式,所以C选项错误;
D、原式=4,所以D选项正确.
故选:D.
7.(2023秋 文昌校级期末)点A(x,y1)在函数y=2x的图象上,点B(x,y2)在y=﹣x+3的图象上,若使y1≥y2则x的取值范围应为( )
A.x≤3 B.x≥3 C.x≤1 D.x≥1
【解答】解:∵点A(x,y1)在函数y=2x的图象上,
∴y1=2x,
∵点B(x,y2)在y=﹣x+3的图象上,
∴y2=﹣x+3,
∵y1≥y2,
∴2x≥﹣x+3,
x≥1,
故选:D.
8.(2023秋 未央区校级期末)如表记录了甲、乙、丙、丁四名跳高运动员最近几次选拔赛成绩的平均数与方差:
甲 乙 丙 丁
平均数(cm) 180 185 180 185
方差 8.1 7.4 3.6 3.6
根据表中数据,要从中选择一名成绩好且发挥稳定的运动员参加比赛,应该选择( )
A.甲 B.乙 C.丙 D.丁
【解答】解:∵,
∴从丁和乙中选择一人参加比赛,
∵丁的方差比乙的方差小,
∴选择丁参赛.
故选:D.
9.(2023秋 金台区期末)我国古代问题:以绳测井,若将绳三折测之,绳多四尺,若将绳四折测之,绳多一尺,绳长、井深各几何?这段话的意思是:用绳子量井深,把绳三折来量,井外余绳四尺,把绳四折来量,井外余绳一尺,绳长、井深各几尺?若设绳长为x尺,井深为y尺,则符合题意的方程组是( )
A. B.
C. D.
【解答】解:设绳长是x尺,井深是y尺,
依题意得:,
故选:D.
10.(2024秋 萧山区月考)如图,分别以直角三角形三边为边长作正方形、半圆、正三角形、直角三角形,不存在S1+S2=S3的面积关系的是( )
A. B.
C. D.
【解答】解:设两直角边分别为x,y,斜边为z,
B中,,,,
∵,
∴S1+S2=S3,故B项不符合题意;
则A中,,
∵x2+y2=z2,
∴S1+S2=S3,故A项不符合题意;
C中,三个三角形是等边三角形,
如图,△ABC的四边长为x,过点A作AD⊥BC于点D,
∵△ABC是等边三角形,AD⊥BC,
∴AB=BC=AC=x,,
∴,
∴,
同理可得:,,
∵,
∴S1+S2=S3,故C项不符合题意;
D中,当各线段长如图时,
,,,
,
∴S1+S2≠S3,故D项符合题意;
故选:D.
二.填空题(共7小题)
11.(2024 包河区二模)命题“如果a,b互为相反数,那么a+b=0”的逆命题为: 如果a+b=0,那么a、b互为相反数 .
【解答】解:命题“如果a、b互为相反数,那么a+b=0”的逆命题是:如果a+b=0,那么a、b互为相反数.
故答案为:如果a+b=0,那么a、b互为相反数.
12.(2024秋 贵州期中)的算术平方根是 3 ,的平方根是 ±2 .
【解答】解:的算术平方根是;的平方根是;
故答案为:3,±2.
13.(2024秋 南海区校级月考)已知点A(6,﹣7),则点A到x轴的距离是 7 .
【解答】解:∵|﹣7|=7,
∴点A(6,﹣7)到x轴的距离是7.
故答案为:7.
14.(2023秋 雁塔区校级期末)若关于x,y的二元一次方程组的解也是x+2y=3的解,则k的值为 .
【解答】解:,
①﹣②得:x+2y=﹣2k,
又∵x+2y=3,
∴﹣2k=3,
解得:,
∴k的值为.
故答案为:.
15.(2023秋 成安县期末)如图,在平面直角坐标系中,直线yx+3交x轴于点A,交y轴于点B,以点A为圆心,AB长为半径画弧,交x轴的负半轴于点C,则直线BC的解析式为 y=3x+3 .
【解答】解:在直线yx+3中,令y=0,求得x=4;令x=0,求得y=3,
∴点A的坐标为(4,0),点B的坐标为(0,3),
∴BO=3,AO=4,
∴AB5,
∵以点A为圆心,AB长为半径画弧,交x轴的负半轴于点C,
∴CO=5﹣4=1,
则点C的坐标为:(﹣1,0),
设直线BC的解析式为y=kx+b,
把B(0,3),C(﹣1,0)代入得,解得,
∴直线BC的解析式为y=3x+3.
故答案为y=3x+3.
16.(2023秋 成都期末)如图,有两棵树,一棵高12米,另一棵高7米,两树相距12米,一只小鸟从一棵树的树梢A飞到另一棵树的树梢B,则小鸟至少要飞行 13 米.
【解答】解:过B作BC∥地面,连接AB,
,
由题意得,BC=12米,AC=12﹣7=5(米),
由勾股定理得,AB13(米),
故答案为:13.
17.(2023秋 西安区校级期末)如图,在△ABC中,AD平分∠BAC,∠BAC,BE平分∠ABC,AD BE,AD、BE交于点O,OF⊥BC,若∠C=70°,∠BAC=60°,则∠DOF= 10° .
【解答】解:∵∠C=70°,∠BAC=60°,
∴∠ABC=180°﹣∠C﹣∠BAC=50°,
∵AD平分∠BAC,
∴,
∴∠ADC=∠ABC+∠BAD=80°,
∵OF⊥BC,
∴∠OFD=90°,
∴∠DOF=90°﹣∠ADC=10°.
故答案为:10°.
三.解答题(共7小题)
18.(2023秋 未央区校级期末)计算:.
【解答】解:原式=﹣2×412+26
=﹣812+126
=18+4.
19.(2023秋 七里河区校级期末)解方程组:
(1);
(2).
【解答】解:(1),
①+②,得:3x=3,解得:x=1,
把x=1代入①,得:1﹣y=4,解得:y=﹣3,
∴原方程组的解为;
(2),
①+②,得:27x+27y=81,即:x+y=3③,
①﹣②,得:﹣x+y=﹣1④,
③+④,得:2y=2,解得:y=1,
把y=1代入③,得:x+1=3,解得:x=2,
∴方程组的解为:.
20.(2023秋 桐城市校级期末)已知一次函数y=(3﹣m)x+2m﹣9的图象与y轴的负半轴相交,y随x的增大而减小,且m为整数.
(1)求m的值.
(2)当﹣1≤x≤2时,求y的取值范围.
【解答】解:(1)∵一次函数y=(3﹣m)x+2m﹣9的图象与y轴的负半轴相交,y随x的增大而减小,
∴,
解得3<m<4.5,
∵m为整数,
∴m=4.
(2)由(1)知,m=4,则该一次函数解析式为:y=﹣x﹣1.
∵﹣1≤x≤2,
∴﹣3≤﹣x﹣1≤0,
即y的取值范围是﹣3≤y≤0.
21.(2023秋 新城区校级期末)2023年12月4日是我国第10个“国家宪法日”,为推动广大学生树立宪法意识、增强法制观念,11月底,全国青少年普法网举办了全国学生“学宪法讲宪法”活动,某中学为了了解九年级学生的答题情况,随机抽取了部分学生的成绩,并将调查结果绘制成了如图所示的统计图.
所抽取该校九年级学生“学宪法讲宪法”活动测试成绩的统计图:
(1)补全两幅统计图;
(2)本次抽查学生成绩的众数是 90 ,中位数是 85 ;
(3)该校九年级学生有1200人,全部参加考试,请估计该校九年级学生在测试中不低于80分的学生有多少人?
【解答】解:(1)∵抽样学生中成绩为8(0分)的有8人,占抽样学生数的16%,
∴本次抽样人数为:8÷16%=50(人),
∴抽样学生中成绩为9(0分)的有:50﹣5﹣12﹣8﹣9=16(人),
补全条形统计图如下:
(2)该组数据中,9(0分)出现的次数最多,
∴众数是90,
把该组数据按从小到大的顺序排列后,第25、26个数都是80,90,
∴该组数据的中位数是,
∴所调查学生测试成绩,众数为90,中位数为85,
故答案为:90,85;
(3)由扇形图知,抽样学生中成绩不少于8(0分)的占:1﹣24%﹣10%=66%,
∴该校九年级学生在体育模拟测试中不低于(8分)的学生约有:1200×66%=792(人),
∴该校九年级学生在体育模拟测试中不低于(8分)的学生约有792人.
22.(2023秋 裕安区校级期末)某礼品店为迎接农历新年的到来,准备购进一批适合学生的礼品.已知购进4件A礼品和12件B礼品共需360元,购进8件A礼品和6件B礼品共需270元.
(1)(列二元一次方程组)求A,B两种礼品每件的进价.
(2)该店计划将5000元全部用于购进A,B这两种礼品,设购进A礼品m件,B礼品n件.
①求n与m之间的关系式;
②该店进货时,厂家要求A礼品的购进数量不少于100件.已知A礼品每件售价为20元,B礼品每件售价为35元.设该店全部售出这两种礼品可获利W元,求W与m之间的关系式和该店所获利润的最大值.
【解答】解:(1)设A礼品每个的进价是x元,B礼品每个的进价是y元,
依题意,,
解.
(2)①依题意,15m+25n=5000,
∴n=200m.
②w=(20﹣15)m+(35﹣25)(200m)=2000﹣m.
∴w随m的增大而减小,且m≥100.
∴当m=100,w取得最大值1900元.
即A礼品进货100件时,该店获利最大为1900元.
23.(2023秋 成安县期末)疫苗接种,利国利民.甲、乙两地分别对本地各40万人接种新冠疫苗.甲地在前期完成5万人接种后,甲、乙两地同时以相同速度接种,甲地经过a天后接种人数达到25万人,由于情况变化,接种速度放缓,结果100天完成接种任务,乙地80天完成接种任务,在某段时间内,甲、乙两地的接种人数y(万人)与各自接种时间x(天)之间的关系如图所示.
(1)求a的值;
(2)当甲地接种速度放缓后,求y关于x的函数解析式;
(3)当乙地完成接种任务时,求甲地未接种疫苗的人数.
【解答】解:(1)由图象可知,乙地80天接种40万人,
∴乙地每天接种的人数为40÷80=0.5(万人),
∵甲、乙两地同时以相同速度接种,
∴甲地在前a天每天接种的人数为0.5万,
∴a40,
答:a的值为40.
(2)设甲地接种速度放缓后,y关于x的函数解析式为:y=kx+b,
将(40,25),(100,40)代入得:
,
解得:,
∴y=0.25x+15.
答:甲地接种速度放缓后,y关于x的函数解析式为y=0.25x+15.
(3)把x=80代入y=0.25x+15得:
y=0.25×80+15=35,
40﹣35=5(万人).
答:乙地完成接种任务时,甲地未接种疫苗的人数为5万人.
24.(2023秋 平南县期末)阅读材料:
【材料一】两个含有二次根式的非零代数式相乘,如果它们的积不含二次根式,那么这两个代数式互为有理化因式,例如:,,我们称的一个有理化因式是,的一个有理化因式是.如果一个代数式的分母中含有二次根式,通常可将分子、分母同乘分母的有理化因式,使分母中不含根号,这种变形叫做分母有理化.例如:,.
【材料二】小明在学习了上述材料后结合所学知识灵活解决问题:已知,求2a2﹣8a+1的值.他是这样分析与解答的:
∵,
∴,
∴(a﹣2)2=3
∴a2﹣4a+4=3,
∴a2﹣4a=﹣1,
∴2a2﹣8a+1=2(a2﹣4a)+1=2×(﹣1)+1=﹣1.
请你根据材料中的方法探索并解决下列问题:
(1)的有理化因式是 ,的有理化因式是 ;(均写出一个即可)
(2)计算:;
(3)若,求3a2﹣6a+5的值.
【解答】解:(1)∵,,
故答案为:,;
(2)
;
(3)∵.
∴
∴(a﹣1)2=3,
∴a2﹣2a+1=3,
∴a2﹣2a=2
∴3a2﹣6a+5=3(a2﹣2a)+5=3×2+5=11.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024-2025学年期末达标测试卷-数学八年级上册北师大版
一.选择题(共10小题)
1.(2024秋 凤城市期中)如图是小刚画的一张脸,如果他用(1,3)表示左眼,用(3,3)表示右眼,那么嘴的位置可以表示成( )
A.(2,1) B.(2,2) C.(2,3) D.(1,2)
2.(2024秋 丰城市校级月考)使二次根式有意义的a的取值范围是( )
A.a≠5 B.a>5 C.a≤5 D.a<5
3.(2023秋 阳城县期末)“数轴上的点并不都表示有理数,如图所示,数轴上的点P所表示的数是”,这种说明问题的方式体现的数学思想是( )
A.方程思想 B.建模思想
C.数形结合思想 D.分类讨论思想
4.(2024 凉州区校级一模)如图,∠ACE是△ABC的外角,BD平分∠ABC,CD平分∠ACE,且BD,CD相交于点D.若∠A=80°,则∠D等于( )
A.30° B.40° C.50° D.55°
5.(2023秋 桐城市校级期末)下列命题:①垂直于同一条直线的两条直线平行;②两直线平行,同位角相等;③对顶角相等;④若ax>a,则x>1;⑤邻补角的平分线互相垂直,其中真命题的个数是( )
A.1 B.2 C.3 D.4
6.(2023秋 凤翔区期末)下列运算正确的是( )
A. B. C. D.
7.(2023秋 文昌校级期末)点A(x,y1)在函数y=2x的图象上,点B(x,y2)在y=﹣x+3的图象上,若使y1≥y2则x的取值范围应为( )
A.x≤3 B.x≥3 C.x≤1 D.x≥1
8.(2023秋 未央区校级期末)如表记录了甲、乙、丙、丁四名跳高运动员最近几次选拔赛成绩的平均数与方差:
甲 乙 丙 丁
平均数(cm) 180 185 180 185
方差 8.1 7.4 3.6 3.6
根据表中数据,要从中选择一名成绩好且发挥稳定的运动员参加比赛,应该选择( )
A.甲 B.乙 C.丙 D.丁
9.(2023秋 金台区期末)我国古代问题:以绳测井,若将绳三折测之,绳多四尺,若将绳四折测之,绳多一尺,绳长、井深各几何?这段话的意思是:用绳子量井深,把绳三折来量,井外余绳四尺,把绳四折来量,井外余绳一尺,绳长、井深各几尺?若设绳长为x尺,井深为y尺,则符合题意的方程组是( )
A. B.
C. D.
10.(2024秋 萧山区月考)如图,分别以直角三角形三边为边长作正方形、半圆、正三角形、直角三角形,不存在S1+S2=S3的面积关系的是( )
A. B.
C. D.
二.填空题(共7小题)
11.(2024 包河区二模)命题“如果a,b互为相反数,那么a+b=0”的逆命题为: .
12.(2024秋 贵州期中)的算术平方根是 ,的平方根是 .
13.(2024秋 南海区校级月考)已知点A(6,﹣7),则点A到x轴的距离是 .
14.(2023秋 雁塔区校级期末)若关于x,y的二元一次方程组的解也是x+2y=3的解,则k的值为 .
15.(2023秋 成安县期末)如图,在平面直角坐标系中,直线yx+3交x轴于点A,交y轴于点B,以点A为圆心,AB长为半径画弧,交x轴的负半轴于点C,则直线BC的解析式为 .
16.(2023秋 成都期末)如图,有两棵树,一棵高12米,另一棵高7米,两树相距12米,一只小鸟从一棵树的树梢A飞到另一棵树的树梢B,则小鸟至少要飞行 米.
17.(2023秋 西安区校级期末)如图,在△ABC中,AD平分∠BAC,∠BAC,BE平分∠ABC,AD BE,AD、BE交于点O,OF⊥BC,若∠C=70°,∠BAC=60°,则∠DOF= .
三.解答题(共7小题)
18.(2023秋 未央区校级期末)计算:.
19.(2023秋 七里河区校级期末)解方程组:
(1);
(2).
20.(2023秋 桐城市校级期末)已知一次函数y=(3﹣m)x+2m﹣9的图象与y轴的负半轴相交,y随x的增大而减小,且m为整数.
(1)求m的值.
(2)当﹣1≤x≤2时,求y的取值范围.
21.(2023秋 新城区校级期末)2023年12月4日是我国第10个“国家宪法日”,为推动广大学生树立宪法意识、增强法制观念,11月底,全国青少年普法网举办了全国学生“学宪法讲宪法”活动,某中学为了了解九年级学生的答题情况,随机抽取了部分学生的成绩,并将调查结果绘制成了如图所示的统计图.
所抽取该校九年级学生“学宪法讲宪法”活动测试成绩的统计图:
(1)补全两幅统计图;
(2)本次抽查学生成绩的众数是 ,中位数是 ;
(3)该校九年级学生有1200人,全部参加考试,请估计该校九年级学生在测试中不低于80分的学生有多少人?
22.(2023秋 裕安区校级期末)某礼品店为迎接农历新年的到来,准备购进一批适合学生的礼品.已知购进4件A礼品和12件B礼品共需360元,购进8件A礼品和6件B礼品共需270元.
(1)(列二元一次方程组)求A,B两种礼品每件的进价.
(2)该店计划将5000元全部用于购进A,B这两种礼品,设购进A礼品m件,B礼品n件.
①求n与m之间的关系式;
②该店进货时,厂家要求A礼品的购进数量不少于100件.已知A礼品每件售价为20元,B礼品每件售价为35元.设该店全部售出这两种礼品可获利W元,求W与m之间的关系式和该店所获利润的最大值.
23.(2023秋 成安县期末)疫苗接种,利国利民.甲、乙两地分别对本地各40万人接种新冠疫苗.甲地在前期完成5万人接种后,甲、乙两地同时以相同速度接种,甲地经过a天后接种人数达到25万人,由于情况变化,接种速度放缓,结果100天完成接种任务,乙地80天完成接种任务,在某段时间内,甲、乙两地的接种人数y(万人)与各自接种时间x(天)之间的关系如图所示.
(1)求a的值;
(2)当甲地接种速度放缓后,求y关于x的函数解析式;
(3)当乙地完成接种任务时,求甲地未接种疫苗的人数.
24.(2023秋 平南县期末)阅读材料:
【材料一】两个含有二次根式的非零代数式相乘,如果它们的积不含二次根式,那么这两个代数式互为有理化因式,例如:,,我们称的一个有理化因式是,的一个有理化因式是.如果一个代数式的分母中含有二次根式,通常可将分子、分母同乘分母的有理化因式,使分母中不含根号,这种变形叫做分母有理化.例如:,.
【材料二】小明在学习了上述材料后结合所学知识灵活解决问题:已知,求2a2﹣8a+1的值.他是这样分析与解答的:
∵,
∴,
∴(a﹣2)2=3
∴a2﹣4a+4=3,
∴a2﹣4a=﹣1,
∴2a2﹣8a+1=2(a2﹣4a)+1=2×(﹣1)+1=﹣1.
请你根据材料中的方法探索并解决下列问题:
(1)的有理化因式是 ,的有理化因式是 ;(均写出一个即可)
(2)计算:;
(3)若,求3a2﹣6a+5的值.
2024-2025学年期末达标测试卷-数学八年级上册北师大版
参考答案与试题解析
题号 1 2 3 4 5 6 7 8 9 10
答案 A C C B C D D D D D
一.选择题(共10小题)
1.(2024秋 凤城市期中)如图是小刚画的一张脸,如果他用(1,3)表示左眼,用(3,3)表示右眼,那么嘴的位置可以表示成( )
A.(2,1) B.(2,2) C.(2,3) D.(1,2)
【解答】解:∵用(1,3)表示左眼,用(3,3)表示右眼,
∴坐标系的位置如图:
∴嘴的位置可以表示成(2,1);
故选:A.
2.(2024秋 丰城市校级月考)使二次根式有意义的a的取值范围是( )
A.a≠5 B.a>5 C.a≤5 D.a<5
【解答】解:由题意得:5﹣a≥0,
解得a≤5,
故选:C.
3.(2023秋 阳城县期末)“数轴上的点并不都表示有理数,如图所示,数轴上的点P所表示的数是”,这种说明问题的方式体现的数学思想是( )
A.方程思想 B.建模思想
C.数形结合思想 D.分类讨论思想
【解答】解:∵数轴上的点并不都表示有理数,如图中数轴上的点P所表示的数是,
这种利用图形直观说明问题的方式A、B、D的说法显然不正确,
∴本题是把数与数轴上的点相联系,是数形结合的思想方法.
故选:C.
4.(2024 凉州区校级一模)如图,∠ACE是△ABC的外角,BD平分∠ABC,CD平分∠ACE,且BD,CD相交于点D.若∠A=80°,则∠D等于( )
A.30° B.40° C.50° D.55°
【解答】解:∵BD平分∠ABC,CD平分∠ACE,
∴∠ABC=2∠DBC,∠ACE=2∠DCE.
∴∠DBC=2∠D.
∵∠A=80°,
∴.
故选:B.
5.(2023秋 桐城市校级期末)下列命题:①垂直于同一条直线的两条直线平行;②两直线平行,同位角相等;③对顶角相等;④若ax>a,则x>1;⑤邻补角的平分线互相垂直,其中真命题的个数是( )
A.1 B.2 C.3 D.4
【解答】解:①垂直于同一条直线的两条直线平行是错误的,要强调同一平面内;
②两直线平行,同位角相等;是正确的;
③对顶角相等;是正确的;
④若ax>a,则x>1是错误的;要强调前提是a>0;
⑤邻补角的平分线互相垂直,是正确的;
故选:C.
6.(2023秋 凤翔区期末)下列运算正确的是( )
A. B. C. D.
【解答】解:A、与不能合并,所以A选项错误;
B、原式=3,所以B选项错误;
C、原式,所以C选项错误;
D、原式=4,所以D选项正确.
故选:D.
7.(2023秋 文昌校级期末)点A(x,y1)在函数y=2x的图象上,点B(x,y2)在y=﹣x+3的图象上,若使y1≥y2则x的取值范围应为( )
A.x≤3 B.x≥3 C.x≤1 D.x≥1
【解答】解:∵点A(x,y1)在函数y=2x的图象上,
∴y1=2x,
∵点B(x,y2)在y=﹣x+3的图象上,
∴y2=﹣x+3,
∵y1≥y2,
∴2x≥﹣x+3,
x≥1,
故选:D.
8.(2023秋 未央区校级期末)如表记录了甲、乙、丙、丁四名跳高运动员最近几次选拔赛成绩的平均数与方差:
甲 乙 丙 丁
平均数(cm) 180 185 180 185
方差 8.1 7.4 3.6 3.6
根据表中数据,要从中选择一名成绩好且发挥稳定的运动员参加比赛,应该选择( )
A.甲 B.乙 C.丙 D.丁
【解答】解:∵,
∴从丁和乙中选择一人参加比赛,
∵丁的方差比乙的方差小,
∴选择丁参赛.
故选:D.
9.(2023秋 金台区期末)我国古代问题:以绳测井,若将绳三折测之,绳多四尺,若将绳四折测之,绳多一尺,绳长、井深各几何?这段话的意思是:用绳子量井深,把绳三折来量,井外余绳四尺,把绳四折来量,井外余绳一尺,绳长、井深各几尺?若设绳长为x尺,井深为y尺,则符合题意的方程组是( )
A. B.
C. D.
【解答】解:设绳长是x尺,井深是y尺,
依题意得:,
故选:D.
10.(2024秋 萧山区月考)如图,分别以直角三角形三边为边长作正方形、半圆、正三角形、直角三角形,不存在S1+S2=S3的面积关系的是( )
A. B.
C. D.
【解答】解:设两直角边分别为x,y,斜边为z,
B中,,,,
∵,
∴S1+S2=S3,故B项不符合题意;
则A中,,
∵x2+y2=z2,
∴S1+S2=S3,故A项不符合题意;
C中,三个三角形是等边三角形,
如图,△ABC的四边长为x,过点A作AD⊥BC于点D,
∵△ABC是等边三角形,AD⊥BC,
∴AB=BC=AC=x,,
∴,
∴,
同理可得:,,
∵,
∴S1+S2=S3,故C项不符合题意;
D中,当各线段长如图时,
,,,
,
∴S1+S2≠S3,故D项符合题意;
故选:D.
二.填空题(共7小题)
11.(2024 包河区二模)命题“如果a,b互为相反数,那么a+b=0”的逆命题为: 如果a+b=0,那么a、b互为相反数 .
【解答】解:命题“如果a、b互为相反数,那么a+b=0”的逆命题是:如果a+b=0,那么a、b互为相反数.
故答案为:如果a+b=0,那么a、b互为相反数.
12.(2024秋 贵州期中)的算术平方根是 3 ,的平方根是 ±2 .
【解答】解:的算术平方根是;的平方根是;
故答案为:3,±2.
13.(2024秋 南海区校级月考)已知点A(6,﹣7),则点A到x轴的距离是 7 .
【解答】解:∵|﹣7|=7,
∴点A(6,﹣7)到x轴的距离是7.
故答案为:7.
14.(2023秋 雁塔区校级期末)若关于x,y的二元一次方程组的解也是x+2y=3的解,则k的值为 .
【解答】解:,
①﹣②得:x+2y=﹣2k,
又∵x+2y=3,
∴﹣2k=3,
解得:,
∴k的值为.
故答案为:.
15.(2023秋 成安县期末)如图,在平面直角坐标系中,直线yx+3交x轴于点A,交y轴于点B,以点A为圆心,AB长为半径画弧,交x轴的负半轴于点C,则直线BC的解析式为 y=3x+3 .
【解答】解:在直线yx+3中,令y=0,求得x=4;令x=0,求得y=3,
∴点A的坐标为(4,0),点B的坐标为(0,3),
∴BO=3,AO=4,
∴AB5,
∵以点A为圆心,AB长为半径画弧,交x轴的负半轴于点C,
∴CO=5﹣4=1,
则点C的坐标为:(﹣1,0),
设直线BC的解析式为y=kx+b,
把B(0,3),C(﹣1,0)代入得,解得,
∴直线BC的解析式为y=3x+3.
故答案为y=3x+3.
16.(2023秋 成都期末)如图,有两棵树,一棵高12米,另一棵高7米,两树相距12米,一只小鸟从一棵树的树梢A飞到另一棵树的树梢B,则小鸟至少要飞行 13 米.
【解答】解:过B作BC∥地面,连接AB,
,
由题意得,BC=12米,AC=12﹣7=5(米),
由勾股定理得,AB13(米),
故答案为:13.
17.(2023秋 西安区校级期末)如图,在△ABC中,AD平分∠BAC,∠BAC,BE平分∠ABC,AD BE,AD、BE交于点O,OF⊥BC,若∠C=70°,∠BAC=60°,则∠DOF= 10° .
【解答】解:∵∠C=70°,∠BAC=60°,
∴∠ABC=180°﹣∠C﹣∠BAC=50°,
∵AD平分∠BAC,
∴,
∴∠ADC=∠ABC+∠BAD=80°,
∵OF⊥BC,
∴∠OFD=90°,
∴∠DOF=90°﹣∠ADC=10°.
故答案为:10°.
三.解答题(共7小题)
18.(2023秋 未央区校级期末)计算:.
【解答】解:原式=﹣2×412+26
=﹣812+126
=18+4.
19.(2023秋 七里河区校级期末)解方程组:
(1);
(2).
【解答】解:(1),
①+②,得:3x=3,解得:x=1,
把x=1代入①,得:1﹣y=4,解得:y=﹣3,
∴原方程组的解为;
(2),
①+②,得:27x+27y=81,即:x+y=3③,
①﹣②,得:﹣x+y=﹣1④,
③+④,得:2y=2,解得:y=1,
把y=1代入③,得:x+1=3,解得:x=2,
∴方程组的解为:.
20.(2023秋 桐城市校级期末)已知一次函数y=(3﹣m)x+2m﹣9的图象与y轴的负半轴相交,y随x的增大而减小,且m为整数.
(1)求m的值.
(2)当﹣1≤x≤2时,求y的取值范围.
【解答】解:(1)∵一次函数y=(3﹣m)x+2m﹣9的图象与y轴的负半轴相交,y随x的增大而减小,
∴,
解得3<m<4.5,
∵m为整数,
∴m=4.
(2)由(1)知,m=4,则该一次函数解析式为:y=﹣x﹣1.
∵﹣1≤x≤2,
∴﹣3≤﹣x﹣1≤0,
即y的取值范围是﹣3≤y≤0.
21.(2023秋 新城区校级期末)2023年12月4日是我国第10个“国家宪法日”,为推动广大学生树立宪法意识、增强法制观念,11月底,全国青少年普法网举办了全国学生“学宪法讲宪法”活动,某中学为了了解九年级学生的答题情况,随机抽取了部分学生的成绩,并将调查结果绘制成了如图所示的统计图.
所抽取该校九年级学生“学宪法讲宪法”活动测试成绩的统计图:
(1)补全两幅统计图;
(2)本次抽查学生成绩的众数是 90 ,中位数是 85 ;
(3)该校九年级学生有1200人,全部参加考试,请估计该校九年级学生在测试中不低于80分的学生有多少人?
【解答】解:(1)∵抽样学生中成绩为8(0分)的有8人,占抽样学生数的16%,
∴本次抽样人数为:8÷16%=50(人),
∴抽样学生中成绩为9(0分)的有:50﹣5﹣12﹣8﹣9=16(人),
补全条形统计图如下:
(2)该组数据中,9(0分)出现的次数最多,
∴众数是90,
把该组数据按从小到大的顺序排列后,第25、26个数都是80,90,
∴该组数据的中位数是,
∴所调查学生测试成绩,众数为90,中位数为85,
故答案为:90,85;
(3)由扇形图知,抽样学生中成绩不少于8(0分)的占:1﹣24%﹣10%=66%,
∴该校九年级学生在体育模拟测试中不低于(8分)的学生约有:1200×66%=792(人),
∴该校九年级学生在体育模拟测试中不低于(8分)的学生约有792人.
22.(2023秋 裕安区校级期末)某礼品店为迎接农历新年的到来,准备购进一批适合学生的礼品.已知购进4件A礼品和12件B礼品共需360元,购进8件A礼品和6件B礼品共需270元.
(1)(列二元一次方程组)求A,B两种礼品每件的进价.
(2)该店计划将5000元全部用于购进A,B这两种礼品,设购进A礼品m件,B礼品n件.
①求n与m之间的关系式;
②该店进货时,厂家要求A礼品的购进数量不少于100件.已知A礼品每件售价为20元,B礼品每件售价为35元.设该店全部售出这两种礼品可获利W元,求W与m之间的关系式和该店所获利润的最大值.
【解答】解:(1)设A礼品每个的进价是x元,B礼品每个的进价是y元,
依题意,,
解.
(2)①依题意,15m+25n=5000,
∴n=200m.
②w=(20﹣15)m+(35﹣25)(200m)=2000﹣m.
∴w随m的增大而减小,且m≥100.
∴当m=100,w取得最大值1900元.
即A礼品进货100件时,该店获利最大为1900元.
23.(2023秋 成安县期末)疫苗接种,利国利民.甲、乙两地分别对本地各40万人接种新冠疫苗.甲地在前期完成5万人接种后,甲、乙两地同时以相同速度接种,甲地经过a天后接种人数达到25万人,由于情况变化,接种速度放缓,结果100天完成接种任务,乙地80天完成接种任务,在某段时间内,甲、乙两地的接种人数y(万人)与各自接种时间x(天)之间的关系如图所示.
(1)求a的值;
(2)当甲地接种速度放缓后,求y关于x的函数解析式;
(3)当乙地完成接种任务时,求甲地未接种疫苗的人数.
【解答】解:(1)由图象可知,乙地80天接种40万人,
∴乙地每天接种的人数为40÷80=0.5(万人),
∵甲、乙两地同时以相同速度接种,
∴甲地在前a天每天接种的人数为0.5万,
∴a40,
答:a的值为40.
(2)设甲地接种速度放缓后,y关于x的函数解析式为:y=kx+b,
将(40,25),(100,40)代入得:
,
解得:,
∴y=0.25x+15.
答:甲地接种速度放缓后,y关于x的函数解析式为y=0.25x+15.
(3)把x=80代入y=0.25x+15得:
y=0.25×80+15=35,
40﹣35=5(万人).
答:乙地完成接种任务时,甲地未接种疫苗的人数为5万人.
24.(2023秋 平南县期末)阅读材料:
【材料一】两个含有二次根式的非零代数式相乘,如果它们的积不含二次根式,那么这两个代数式互为有理化因式,例如:,,我们称的一个有理化因式是,的一个有理化因式是.如果一个代数式的分母中含有二次根式,通常可将分子、分母同乘分母的有理化因式,使分母中不含根号,这种变形叫做分母有理化.例如:,.
【材料二】小明在学习了上述材料后结合所学知识灵活解决问题:已知,求2a2﹣8a+1的值.他是这样分析与解答的:
∵,
∴,
∴(a﹣2)2=3
∴a2﹣4a+4=3,
∴a2﹣4a=﹣1,
∴2a2﹣8a+1=2(a2﹣4a)+1=2×(﹣1)+1=﹣1.
请你根据材料中的方法探索并解决下列问题:
(1)的有理化因式是 ,的有理化因式是 ;(均写出一个即可)
(2)计算:;
(3)若,求3a2﹣6a+5的值.
【解答】解:(1)∵,,
故答案为:,;
(2)
;
(3)∵.
∴
∴(a﹣1)2=3,
∴a2﹣2a+1=3,
∴a2﹣2a=2
∴3a2﹣6a+5=3(a2﹣2a)+5=3×2+5=11.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
