2024-2025学年各地区期末试题重组练习(含解析)-数学九年级上册苏科版
文档属性
| 名称 | 2024-2025学年各地区期末试题重组练习(含解析)-数学九年级上册苏科版 |

|
|
| 格式 | doc | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-10 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2024-2025学年各地区期末试题重组练习-数学九年级上册苏科版
一.选择题(共9小题)
1.(2023秋 永年区期末)某校举办了以“展礼仪风采,树文明形象”为主题的比赛.已知某位选手的礼仪服装、语言表达、举止形态这三项的得分分别为90分,80分,80分,若依次按照30%,45%,25%的百分比确定成绩,则该选手的成绩是( )
A.86分 B.85分 C.84分 D.83分
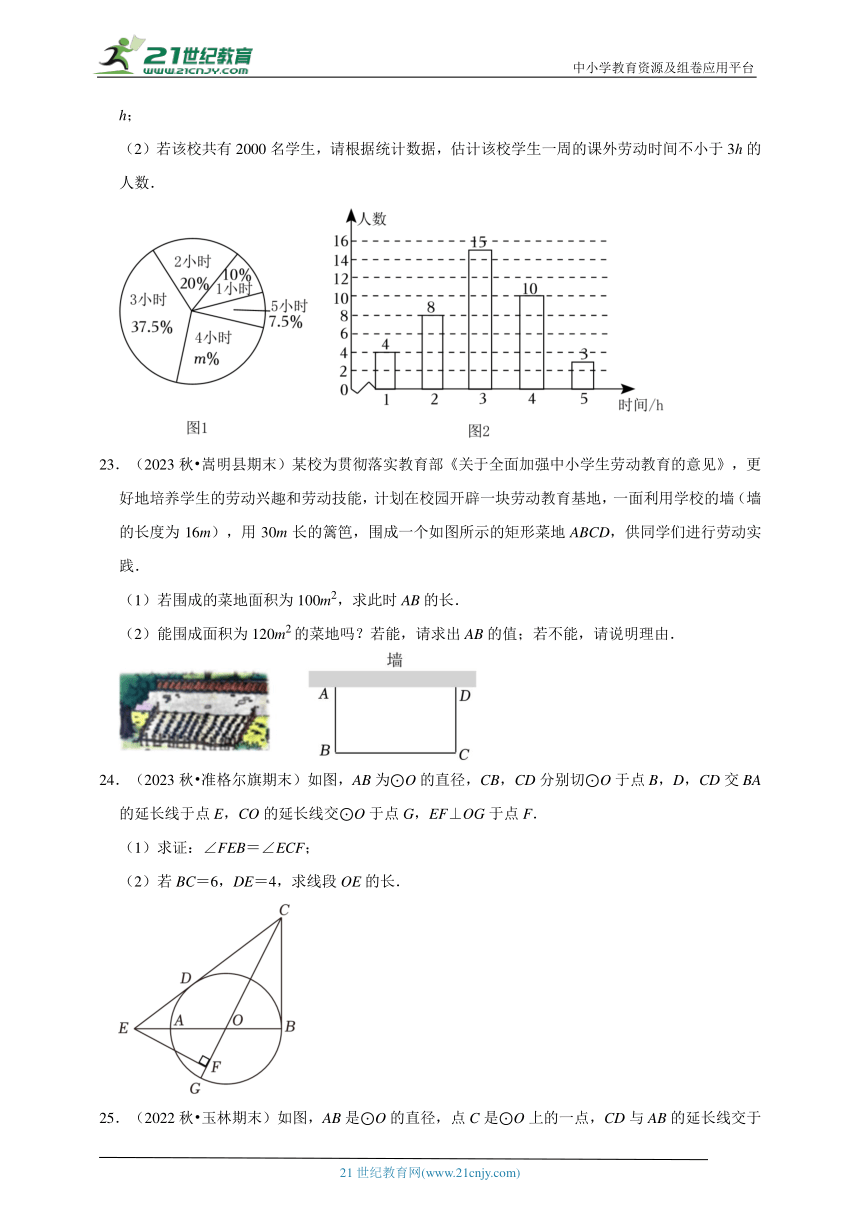
2.(2023秋 琼中县期末)下列是一元二次方程的是( )
A.x3﹣x﹣1=0 B.2x﹣1=5 C. D.x2﹣3x+1=0
3.(2023秋 晋城期末)某校准备组织红色研学活动,需要从晋西北会议旧址、国民师范革命活动旧址、太原解放纪念馆旧址、晋绥八分区旧址四个红色教育基地中任选一个前往研学,则选中晋西北会议旧址的概率为( )
A. B. C. D.
4.(2023秋 盂县期末)一元二次方程x2﹣4=4x的根的情况为( )
A.有两个相等的实数根 B.有两个不等的实数根
C.没有实数根 D.有一个实数根
5.(2023秋 耒阳市校级期末)已知圆锥的母线长为2,底面半径为1,则该圆锥的侧面展开图的面积为( )
A. B.π C.2π D.4π
6.(2023秋 兖州区期末)如图,AB是半圆的直径,CD为半圆的弦,且CD∥AB,∠ACD=36°,则∠B等于( )
A.36° B.46° C.54° D.72°
7.(2023秋 和田地区期末)如图,AB是⊙O的直径,弦CD⊥AB于点E,OC=5cm,CD=8cm,则BE=( )cm.
A.5 B.4 C.3 D.2
8.(2023秋 白水县期末)如图,若一个正六边形的对角线AB的长为10,则正六边形外接圆的半径为( )
A.8 B.6 C.5 D.4
9.(2023秋 东昌府区校级期末)某机械厂七月份生产零件100万个,第三季度生产零件392万个.设该厂八、九月份平均每月的增长率为x,那么x满足的方程是( )
A.100(1+x)2=392
B.100+100(1+x)2=392
C.100+100(1+x)+100(1+2x)=392
D.100+100(1+x)+100(1+x)2=392
二.填空题(共9小题)
10.(2024春 乳山市期末)如果所示的地板由15块方砖组成,每一块方砖除颜色外完全相同,小球自由滚动,随机停在黑色方砖的概率为 .
11.(2023秋 巩义市期末)如图是一个可以自由转动的质地均匀的转盘,被分成12个相同的小扇形.若把某些小扇形涂上红色,使转动的转盘停止时,指针指向红色的概率是,则涂上红色的小扇形有
个.
12.(2023秋 渭城区期末)测试中心分别从操作系统、硬件规格、屏幕尺寸、电池寿命四个项目对新投入市场的一款智能手机进行测评,这款手机的各项得分如下表:
测试项目 操作系统 硬件规格 屏幕尺寸 电池寿命
项目成绩/分 7 8 9 6
最后将四项成绩按3:3:2:2的比例计算综合成绩,则该手机的综合成绩为 分.
13.(2023秋 蒙阴县期末)若x1,x2是一元二次方程x2+2x﹣k﹣1=0的两根,且x1x2=﹣3,则k的值为 .
14.(2023秋 岚山区期末)数字下乡,农货上行,直播逐渐成为农户销售农产品的重要渠道,某地农村网商2021年为1500家,2023年达到2160家,设2021年到2023年农村网商的月平均增长率为x,根据题意可列方程为 .
15.(2023秋 电白区期末)如图,是一个长为30m,宽为20m的矩形花园,现要在花园中修建等宽的小道,剩余的地方种植花草.如图所示,要使种植花草的面积为532m2,那么小道进出口的宽度应为 米.
16.(2023秋 广饶县期末)如图,点A,B,C在半径为2的⊙O上,若∠BAC=30°,则弦BC= .
17.(2023秋 陇县期末)如图,A,B,C为⊙O上的三点,∠AOB=4∠BOC,若∠ACB=60°,则∠BAC的度数是 .
18.(2023秋 东昌府区校级期末)如图,若⊙O的半径为1,则⊙O的内接正八边形AEBFCGDH的面积为 .
三.解答题(共8小题)
19.(2023秋 平定县期末)解方程.
(1)3x2﹣2x﹣7=0.
(2)(2x+1)(5x﹣3)=﹣2(3﹣5x).
20.(2024春 阳山县期末)一个不透明的袋中装有18个白球和若干个红球,它们除颜色外其他均相同.已知将袋中球摇匀后,从中任意摸出一个球是白球的概率是.
(1)求袋中总共有多少个球?
(2)从袋中取走10个球(其中没有红球)并将袋中球摇匀后,求从剩余的球中任意摸出一个球是红球的概率.
21.(2023秋 曹县期末)某商场2023年九月份的销售额为200万元,十月份的销售额下降了20%,商场从十一月份起加强管理,改善经营,使销售额稳步上升,十二月份的销售额达到了193.6万元,若十一月、十二月销售额增长的百分率相同,求十一月份的销售额是多少万元?
22.(2023秋 宿城区期末)2022年3月25日,教育部印发《义务教育课程方案和课程标准(2022年版)》,优化了课程设置,将劳动从综合实践活动课程中独立出来.某校为了解该校学生一周的课外劳动情况,随机抽取部分学生调查了他们一周的课外劳动时间,将数据进行整理并制成如一统计图.
请根据图中提供的信息,解答下列的问题:
(1)求图1中的m= ,本次调查数据的中位数是 h,本次调查数据的众数是 h;
(2)若该校共有2000名学生,请根据统计数据,估计该校学生一周的课外劳动时间不小于3h的人数.
23.(2023秋 嵩明县期末)某校为贯彻落实教育部《关于全面加强中小学生劳动教育的意见》,更好地培养学生的劳动兴趣和劳动技能,计划在校园开辟一块劳动教育基地,一面利用学校的墙(墙的长度为16m),用30m长的篱笆,围成一个如图所示的矩形菜地ABCD,供同学们进行劳动实践.
(1)若围成的菜地面积为100m2,求此时AB的长.
(2)能围成面积为120m2的菜地吗?若能,请求出AB的值;若不能,请说明理由.
24.(2023秋 准格尔旗期末)如图,AB为⊙O的直径,CB,CD分别切⊙O于点B,D,CD交BA的延长线于点E,CO的延长线交⊙O于点G,EF⊥OG于点F.
(1)求证:∠FEB=∠ECF;
(2)若BC=6,DE=4,求线段OE的长.
25.(2022秋 玉林期末)如图,AB是⊙O的直径,点C是⊙O上的一点,CD与AB的延长线交于点D,已知:CA=CD,∠A=30°.
(1)求证:CD是⊙O的切线;
(2)过点B作BE⊥CD于点E,若⊙O的半径为2,求图中阴影部分的面积.
26.(2023秋 东莞市校级期末)HUAWEIMate60Pro是华为技术有限公司于2023年8月29日上架的一款全球首款支持卫星通话的大众智能手机,即使在没有地面网络信号的情况下,也可以拨打接听卫星电话,该手机还支持AI隔空操控、智感支付、注视不熄屏等智慧功能等.该系列完成了核心技术领域从0到1的跃迁,让无数国人为之自豪并被赞誉为“争气机”.手机背面有一条圆弧,象征着以山河之美致敬奔腾不息的力量.如图,圆弧对应的弦AB长80mm,半径OC⊥AB,垂足为D,弓形高CD长14mm.
(1)求AD的长;
(2)求半径OA的长.
2024-2025学年各地区期末试题重组练习-数学九年级上册苏科版
参考答案与试题解析
题号 1 2 3 4 5 6 7 8 9
答案 D D D B C C D C D
一.选择题(共9小题)
1.(2023秋 永年区期末)某校举办了以“展礼仪风采,树文明形象”为主题的比赛.已知某位选手的礼仪服装、语言表达、举止形态这三项的得分分别为90分,80分,80分,若依次按照30%,45%,25%的百分比确定成绩,则该选手的成绩是( )
A.86分 B.85分 C.84分 D.83分
【解答】解:根据题意得:
90×30%+80×45%+80×25%=83(分),
故选:D.
2.(2023秋 琼中县期末)下列是一元二次方程的是( )
A.x3﹣x﹣1=0 B.2x﹣1=5 C. D.x2﹣3x+1=0
【解答】解:A:x3﹣x﹣1=0未知数的最高次数是3,不符合题意;
B:2x﹣1=5未知数的最高次数是1,不符合题意;
C:是分式方程,不符合题意;
D:x2﹣3x+1=0符合一元二次方程的定义;
故选:D.
3.(2023秋 晋城期末)某校准备组织红色研学活动,需要从晋西北会议旧址、国民师范革命活动旧址、太原解放纪念馆旧址、晋绥八分区旧址四个红色教育基地中任选一个前往研学,则选中晋西北会议旧址的概率为( )
A. B. C. D.
【解答】解:∵红色教育基地有4个,
∴选中晋西北会议旧址的概率为.
故选:D.
4.(2023秋 盂县期末)一元二次方程x2﹣4=4x的根的情况为( )
A.有两个相等的实数根 B.有两个不等的实数根
C.没有实数根 D.有一个实数根
【解答】解:∵x2﹣4=4x,
∴x2﹣4x﹣4=0,
∴Δ=(﹣4)2﹣4×(﹣4)×1=16+16=32>0,
∴原方程有两个不相等的实数根,
故选:B.
5.(2023秋 耒阳市校级期末)已知圆锥的母线长为2,底面半径为1,则该圆锥的侧面展开图的面积为( )
A. B.π C.2π D.4π
【解答】解:∵圆锥的底面圆半径为1,
∴圆锥的底面周长为:2π,
∴圆锥的侧面展开图扇形的弧长为2π,
∴圆锥的侧面积为:×2π×2=2π,
故选:C.
6.(2023秋 兖州区期末)如图,AB是半圆的直径,CD为半圆的弦,且CD∥AB,∠ACD=36°,则∠B等于( )
A.36° B.46° C.54° D.72°
【解答】解:∵CD∥AB,
∴∠BAC=∠ACD=36°,
∵AB是半圆的直径,
∴∠ACB=90°,
∴∠ABC=90°﹣∠BAC
=90°﹣36°
=54°;
故选:C.
7.(2023秋 和田地区期末)如图,AB是⊙O的直径,弦CD⊥AB于点E,OC=5cm,CD=8cm,则BE=( )cm.
A.5 B.4 C.3 D.2
【解答】解:∵AB是⊙O的直径,
∴OB=OC=5cm,
∵弦CD⊥AB,
∴CE=DE=4cm,
在Rt△OCE中,OC=5cm,
∴,
∴BE=OB﹣OE=5﹣3=2(cm).
故选:D.
8.(2023秋 白水县期末)如图,若一个正六边形的对角线AB的长为10,则正六边形外接圆的半径为( )
A.8 B.6 C.5 D.4
【解答】解:取对角线AB的中点O,
∵点A与点B关于点O对称,且顶点A与顶点B关于正六边形的中心对称,
∴点O是该正六边形的中心,
∴OA是该正六边形的半径,即该正六边形外接圆的半径,
∴AB=10,
∴OA=OB=AB=5,
故选:C.
9.(2023秋 东昌府区校级期末)某机械厂七月份生产零件100万个,第三季度生产零件392万个.设该厂八、九月份平均每月的增长率为x,那么x满足的方程是( )
A.100(1+x)2=392
B.100+100(1+x)2=392
C.100+100(1+x)+100(1+2x)=392
D.100+100(1+x)+100(1+x)2=392
【解答】解:设该厂八、九月份平均每月的增长率为x,
根据题意可列方程:100+100(1+x)+100(1+x)2=392,
故选:D.
二.填空题(共9小题)
10.(2024春 乳山市期末)如果所示的地板由15块方砖组成,每一块方砖除颜色外完全相同,小球自由滚动,随机停在黑色方砖的概率为 .
【解答】解:∵总面积为15块方砖的面积,其中黑色方砖有5个,
∴小球停在黑色方砖的概率为=,
故答案为:.
11.(2023秋 巩义市期末)如图是一个可以自由转动的质地均匀的转盘,被分成12个相同的小扇形.若把某些小扇形涂上红色,使转动的转盘停止时,指针指向红色的概率是,则涂上红色的小扇形有 2 个.
【解答】解:由题意得,涂上红色的小扇形有(个);
故答案为:2.
12.(2023秋 渭城区期末)测试中心分别从操作系统、硬件规格、屏幕尺寸、电池寿命四个项目对新投入市场的一款智能手机进行测评,这款手机的各项得分如下表:
测试项目 操作系统 硬件规格 屏幕尺寸 电池寿命
项目成绩/分 7 8 9 6
最后将四项成绩按3:3:2:2的比例计算综合成绩,则该手机的综合成绩为 7.5 分.
【解答】解:由题意知,该手机的综合成绩为(分).
故答案为:7.5.
13.(2023秋 蒙阴县期末)若x1,x2是一元二次方程x2+2x﹣k﹣1=0的两根,且x1x2=﹣3,则k的值为 2 .
【解答】解:∵x1,x2是一元二次方程x2+2x﹣k﹣1=0的两根,且x1x2=﹣3,
∴﹣k﹣1=﹣3,
∴k=2.
故答案为:2.
14.(2023秋 岚山区期末)数字下乡,农货上行,直播逐渐成为农户销售农产品的重要渠道,某地农村网商2021年为1500家,2023年达到2160家,设2021年到2023年农村网商的月平均增长率为x,根据题意可列方程为 1500(x+1)2=2160 .
【解答】解:设2021年到2023年农村网商的月平均增长率为x,
由题意得,1500(1+x)2=2160,
故答案为:1500(1+x)2=2160.
15.(2023秋 电白区期末)如图,是一个长为30m,宽为20m的矩形花园,现要在花园中修建等宽的小道,剩余的地方种植花草.如图所示,要使种植花草的面积为532m2,那么小道进出口的宽度应为 1 米.
【解答】解:设小道进出口的宽度为x米,依题意得(30﹣2x)(20﹣x)=532,
整理,得x2﹣35x+34=0.
解得,x1=1,x2=34.
∵34>30(不合题意,舍去),
∴x=1.
答:小道进出口的宽度应为1米.
故答案为:1.
16.(2023秋 广饶县期末)如图,点A,B,C在半径为2的⊙O上,若∠BAC=30°,则弦BC= 2 .
【解答】解:∵∠BAC=30°,OB=OC=2,
∴∠BOC=2∠A=2×30°=60°,
∵OB=OC,
∴△OBC为等边三角形,
∴BC=OB=2,
故答案为:2.
17.(2023秋 陇县期末)如图,A,B,C为⊙O上的三点,∠AOB=4∠BOC,若∠ACB=60°,则∠BAC的度数是 15° .
【解答】解;∵∠ACB=60°,
∴∠AOB=2∠ACB=120°,
∵∠AOB=4∠BOC,
∴∠BOC=30°,
∴,
故答案为:15°.
18.(2023秋 东昌府区校级期末)如图,若⊙O的半径为1,则⊙O的内接正八边形AEBFCGDH的面积为 .
【解答】解:连接AC,OD,OH,
∵四边形ABCD是圆内接正四边形,∠ADC=90°,
∴AC是圆的直径,AC=2,
∵AD2+CD2=AC2,
∴,
∵DH=AH,
∴弧DH=弧AH,
∴OH⊥AD,
∴,
故答案为:.
三.解答题(共8小题)
19.(2023秋 平定县期末)解方程.
(1)3x2﹣2x﹣7=0.
(2)(2x+1)(5x﹣3)=﹣2(3﹣5x).
【解答】解:(1)3x2﹣2x﹣7=0,
a=3,b=﹣2,c=﹣7,
Δ=b2﹣4ac=4+84=88>0,
∴方程有两个不相等的实数根.
,
∴,.
(2)(2x+1)(5x﹣3)=﹣2(3﹣5x),
方程可变形为(2x+1)(5x﹣3)﹣2(5x﹣3)=0,
因式分解,得(2x﹣1)(5x﹣3)=0,
所以得2x﹣1=0,或5x﹣3=0,
∴,.
20.(2024春 阳山县期末)一个不透明的袋中装有18个白球和若干个红球,它们除颜色外其他均相同.已知将袋中球摇匀后,从中任意摸出一个球是白球的概率是.
(1)求袋中总共有多少个球?
(2)从袋中取走10个球(其中没有红球)并将袋中球摇匀后,求从剩余的球中任意摸出一个球是红球的概率.
【解答】解:(1)设袋中总共有x个球,
∵袋中装有18个白球,从中任意摸出一个球是白球的概率是,
∴=,
解得x=30,
经检验,x=30是原方程的解,
即袋中总共有30个球;
(2)袋子中红球的个数为:30﹣18=12(个),
取走10个球,则袋子中球的总个数为30﹣10=20(个),
∴剩余的球中任意摸出一个球是红球的概率为=.
21.(2023秋 曹县期末)某商场2023年九月份的销售额为200万元,十月份的销售额下降了20%,商场从十一月份起加强管理,改善经营,使销售额稳步上升,十二月份的销售额达到了193.6万元,若十一月、十二月销售额增长的百分率相同,求十一月份的销售额是多少万元?
【解答】解:设十一月、十二月销售额增长的百分率为x,
根据题意,得200×(1﹣20%)(1+x)2=193.6,
解这个方程,得x1=0.1=10%,x2=﹣2.1(不合题意,舍去),
∴200×(1﹣20%)×(1+10%)=176(万元).
答:十一月份的销售额为176万元.
22.(2023秋 宿城区期末)2022年3月25日,教育部印发《义务教育课程方案和课程标准(2022年版)》,优化了课程设置,将劳动从综合实践活动课程中独立出来.某校为了解该校学生一周的课外劳动情况,随机抽取部分学生调查了他们一周的课外劳动时间,将数据进行整理并制成如一统计图.
请根据图中提供的信息,解答下列的问题:
(1)求图1中的m= 25 ,本次调查数据的中位数是 3 h,本次调查数据的众数是 3 h;
(2)若该校共有2000名学生,请根据统计数据,估计该校学生一周的课外劳动时间不小于3h的人数.
【解答】解:(1)4÷10%=40人,
∴参与调查的学生人数为40人,
∴,
∴m=25,
∵参与调查的学生人数一共有40人,将他们的劳动时间从低到高排列,处在第20名和第21名的劳动时间分别为3h,3h
∴中位数为,
由条形统计图可知,劳动时间为3h的人数最多,
∴众数为3h,
故答案为:25,3,3;
(2)解:(人),
答:估计该校学生一周的课外劳动时间不小于3h的人数为1400人.
23.(2023秋 嵩明县期末)某校为贯彻落实教育部《关于全面加强中小学生劳动教育的意见》,更好地培养学生的劳动兴趣和劳动技能,计划在校园开辟一块劳动教育基地,一面利用学校的墙(墙的长度为16m),用30m长的篱笆,围成一个如图所示的矩形菜地ABCD,供同学们进行劳动实践.
(1)若围成的菜地面积为100m2,求此时AB的长.
(2)能围成面积为120m2的菜地吗?若能,请求出AB的值;若不能,请说明理由.
【解答】解:(1)设AB的长为x米,则BC的长为(30﹣2x)米,
根据题意得:x(30﹣2x)=100,
整理得:x2﹣15x+50=0,
解得:x1=5,x2=10,
当x=5时,30﹣2x=30﹣2×5=20>16,不符合题意,舍去;
当x=10时,30﹣2x=30﹣2×10=10<16,符合题意.
答:AB的长为10米;
(2)不能围成面积为120m2的菜地,理由入下:
假设能围成面积为120m2的菜地,设AB的长为y米,则BC的长为(30﹣2y)米,
根据题意得:y(30﹣2y)=120,
整理得:y2﹣15y+60=0,
∵Δ=152﹣4×1×60=﹣15<0,
∴原方程没有实数根,
∴假设不成立,即不能围成面积为120m的菜地.
24.(2023秋 准格尔旗期末)如图,AB为⊙O的直径,CB,CD分别切⊙O于点B,D,CD交BA的延长线于点E,CO的延长线交⊙O于点G,EF⊥OG于点F.
(1)求证:∠FEB=∠ECF;
(2)若BC=6,DE=4,求线段OE的长.
【解答】(1)证明:∵CB,CD分别切⊙O于点B,D,
∴OC平分∠BCE,即∠ECO=∠BCO,OB⊥BC,
∴∠BCO+∠COB=90°,
∵EF⊥OG,
∴∠FEB+∠FOE=90°,
而∠COB=∠FOE,
∴∠FEB=∠ECF;
(2)解:连接OD,如图,
∵CB,CD分别切⊙O于点B,D,
∴CD=CB=6,OD⊥CE,
∴CE=CD+DE=6+4=10,
在Rt△BCE中,,
设⊙O的半径为r,则OD=OB=r,OE=8﹣r,
在Rt△ODE中,r2+42=(8﹣r)2,
解得r=3,
∴OE=8﹣3=5.
25.(2022秋 玉林期末)如图,AB是⊙O的直径,点C是⊙O上的一点,CD与AB的延长线交于点D,已知:CA=CD,∠A=30°.
(1)求证:CD是⊙O的切线;
(2)过点B作BE⊥CD于点E,若⊙O的半径为2,求图中阴影部分的面积.
【解答】(1)证明:连接OC,
∵OA=OC,
∴∠OCA=∠A=30°,
∴∠COD=60°,
又CA=CD,
∴∠D=∠A=30°,
∴∠OCD=180°﹣60°﹣30°=90°,
∴半径OC⊥CD,
∴CD是⊙O的切线;
(2)解:∵OC=2,∠A=∠D=30°,∠OCD=90°,
∴OD=2OC=4,
又OB=2,
∴BD=OB=2,即点B是OD的中点,
又∵BE⊥CD,
∴BE∥OC,BE是△OCD的中位线,
∴,
∴,
∴S阴=S梯形OBEC﹣S扇形OBC
=
=.
26.(2023秋 东莞市校级期末)HUAWEIMate60Pro是华为技术有限公司于2023年8月29日上架的一款全球首款支持卫星通话的大众智能手机,即使在没有地面网络信号的情况下,也可以拨打接听卫星电话,该手机还支持AI隔空操控、智感支付、注视不熄屏等智慧功能等.该系列完成了核心技术领域从0到1的跃迁,让无数国人为之自豪并被赞誉为“争气机”.手机背面有一条圆弧,象征着以山河之美致敬奔腾不息的力量.如图,圆弧对应的弦AB长80mm,半径OC⊥AB,垂足为D,弓形高CD长14mm.
(1)求AD的长;
(2)求半径OA的长.
【解答】解:(1)∵OC⊥AB,AB=80mm,
∴;
(2)∵OC⊥AB,
∴∠ADO=90°,
设半径OA=x mm,则OC=OA=x mm,OD=OC﹣CD=(x﹣14)mm,
∴AD2+OD2=OA2,
402+(x﹣14)2=x2,
1600+x2﹣28x+196=x2,
28x=1796,
,
∴半径OA的长为.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024-2025学年各地区期末试题重组练习-数学九年级上册苏科版
一.选择题(共9小题)
1.(2023秋 永年区期末)某校举办了以“展礼仪风采,树文明形象”为主题的比赛.已知某位选手的礼仪服装、语言表达、举止形态这三项的得分分别为90分,80分,80分,若依次按照30%,45%,25%的百分比确定成绩,则该选手的成绩是( )
A.86分 B.85分 C.84分 D.83分
2.(2023秋 琼中县期末)下列是一元二次方程的是( )
A.x3﹣x﹣1=0 B.2x﹣1=5 C. D.x2﹣3x+1=0
3.(2023秋 晋城期末)某校准备组织红色研学活动,需要从晋西北会议旧址、国民师范革命活动旧址、太原解放纪念馆旧址、晋绥八分区旧址四个红色教育基地中任选一个前往研学,则选中晋西北会议旧址的概率为( )
A. B. C. D.
4.(2023秋 盂县期末)一元二次方程x2﹣4=4x的根的情况为( )
A.有两个相等的实数根 B.有两个不等的实数根
C.没有实数根 D.有一个实数根
5.(2023秋 耒阳市校级期末)已知圆锥的母线长为2,底面半径为1,则该圆锥的侧面展开图的面积为( )
A. B.π C.2π D.4π
6.(2023秋 兖州区期末)如图,AB是半圆的直径,CD为半圆的弦,且CD∥AB,∠ACD=36°,则∠B等于( )
A.36° B.46° C.54° D.72°
7.(2023秋 和田地区期末)如图,AB是⊙O的直径,弦CD⊥AB于点E,OC=5cm,CD=8cm,则BE=( )cm.
A.5 B.4 C.3 D.2
8.(2023秋 白水县期末)如图,若一个正六边形的对角线AB的长为10,则正六边形外接圆的半径为( )
A.8 B.6 C.5 D.4
9.(2023秋 东昌府区校级期末)某机械厂七月份生产零件100万个,第三季度生产零件392万个.设该厂八、九月份平均每月的增长率为x,那么x满足的方程是( )
A.100(1+x)2=392
B.100+100(1+x)2=392
C.100+100(1+x)+100(1+2x)=392
D.100+100(1+x)+100(1+x)2=392
二.填空题(共9小题)
10.(2024春 乳山市期末)如果所示的地板由15块方砖组成,每一块方砖除颜色外完全相同,小球自由滚动,随机停在黑色方砖的概率为 .
11.(2023秋 巩义市期末)如图是一个可以自由转动的质地均匀的转盘,被分成12个相同的小扇形.若把某些小扇形涂上红色,使转动的转盘停止时,指针指向红色的概率是,则涂上红色的小扇形有
个.
12.(2023秋 渭城区期末)测试中心分别从操作系统、硬件规格、屏幕尺寸、电池寿命四个项目对新投入市场的一款智能手机进行测评,这款手机的各项得分如下表:
测试项目 操作系统 硬件规格 屏幕尺寸 电池寿命
项目成绩/分 7 8 9 6
最后将四项成绩按3:3:2:2的比例计算综合成绩,则该手机的综合成绩为 分.
13.(2023秋 蒙阴县期末)若x1,x2是一元二次方程x2+2x﹣k﹣1=0的两根,且x1x2=﹣3,则k的值为 .
14.(2023秋 岚山区期末)数字下乡,农货上行,直播逐渐成为农户销售农产品的重要渠道,某地农村网商2021年为1500家,2023年达到2160家,设2021年到2023年农村网商的月平均增长率为x,根据题意可列方程为 .
15.(2023秋 电白区期末)如图,是一个长为30m,宽为20m的矩形花园,现要在花园中修建等宽的小道,剩余的地方种植花草.如图所示,要使种植花草的面积为532m2,那么小道进出口的宽度应为 米.
16.(2023秋 广饶县期末)如图,点A,B,C在半径为2的⊙O上,若∠BAC=30°,则弦BC= .
17.(2023秋 陇县期末)如图,A,B,C为⊙O上的三点,∠AOB=4∠BOC,若∠ACB=60°,则∠BAC的度数是 .
18.(2023秋 东昌府区校级期末)如图,若⊙O的半径为1,则⊙O的内接正八边形AEBFCGDH的面积为 .
三.解答题(共8小题)
19.(2023秋 平定县期末)解方程.
(1)3x2﹣2x﹣7=0.
(2)(2x+1)(5x﹣3)=﹣2(3﹣5x).
20.(2024春 阳山县期末)一个不透明的袋中装有18个白球和若干个红球,它们除颜色外其他均相同.已知将袋中球摇匀后,从中任意摸出一个球是白球的概率是.
(1)求袋中总共有多少个球?
(2)从袋中取走10个球(其中没有红球)并将袋中球摇匀后,求从剩余的球中任意摸出一个球是红球的概率.
21.(2023秋 曹县期末)某商场2023年九月份的销售额为200万元,十月份的销售额下降了20%,商场从十一月份起加强管理,改善经营,使销售额稳步上升,十二月份的销售额达到了193.6万元,若十一月、十二月销售额增长的百分率相同,求十一月份的销售额是多少万元?
22.(2023秋 宿城区期末)2022年3月25日,教育部印发《义务教育课程方案和课程标准(2022年版)》,优化了课程设置,将劳动从综合实践活动课程中独立出来.某校为了解该校学生一周的课外劳动情况,随机抽取部分学生调查了他们一周的课外劳动时间,将数据进行整理并制成如一统计图.
请根据图中提供的信息,解答下列的问题:
(1)求图1中的m= ,本次调查数据的中位数是 h,本次调查数据的众数是 h;
(2)若该校共有2000名学生,请根据统计数据,估计该校学生一周的课外劳动时间不小于3h的人数.
23.(2023秋 嵩明县期末)某校为贯彻落实教育部《关于全面加强中小学生劳动教育的意见》,更好地培养学生的劳动兴趣和劳动技能,计划在校园开辟一块劳动教育基地,一面利用学校的墙(墙的长度为16m),用30m长的篱笆,围成一个如图所示的矩形菜地ABCD,供同学们进行劳动实践.
(1)若围成的菜地面积为100m2,求此时AB的长.
(2)能围成面积为120m2的菜地吗?若能,请求出AB的值;若不能,请说明理由.
24.(2023秋 准格尔旗期末)如图,AB为⊙O的直径,CB,CD分别切⊙O于点B,D,CD交BA的延长线于点E,CO的延长线交⊙O于点G,EF⊥OG于点F.
(1)求证:∠FEB=∠ECF;
(2)若BC=6,DE=4,求线段OE的长.
25.(2022秋 玉林期末)如图,AB是⊙O的直径,点C是⊙O上的一点,CD与AB的延长线交于点D,已知:CA=CD,∠A=30°.
(1)求证:CD是⊙O的切线;
(2)过点B作BE⊥CD于点E,若⊙O的半径为2,求图中阴影部分的面积.
26.(2023秋 东莞市校级期末)HUAWEIMate60Pro是华为技术有限公司于2023年8月29日上架的一款全球首款支持卫星通话的大众智能手机,即使在没有地面网络信号的情况下,也可以拨打接听卫星电话,该手机还支持AI隔空操控、智感支付、注视不熄屏等智慧功能等.该系列完成了核心技术领域从0到1的跃迁,让无数国人为之自豪并被赞誉为“争气机”.手机背面有一条圆弧,象征着以山河之美致敬奔腾不息的力量.如图,圆弧对应的弦AB长80mm,半径OC⊥AB,垂足为D,弓形高CD长14mm.
(1)求AD的长;
(2)求半径OA的长.
2024-2025学年各地区期末试题重组练习-数学九年级上册苏科版
参考答案与试题解析
题号 1 2 3 4 5 6 7 8 9
答案 D D D B C C D C D
一.选择题(共9小题)
1.(2023秋 永年区期末)某校举办了以“展礼仪风采,树文明形象”为主题的比赛.已知某位选手的礼仪服装、语言表达、举止形态这三项的得分分别为90分,80分,80分,若依次按照30%,45%,25%的百分比确定成绩,则该选手的成绩是( )
A.86分 B.85分 C.84分 D.83分
【解答】解:根据题意得:
90×30%+80×45%+80×25%=83(分),
故选:D.
2.(2023秋 琼中县期末)下列是一元二次方程的是( )
A.x3﹣x﹣1=0 B.2x﹣1=5 C. D.x2﹣3x+1=0
【解答】解:A:x3﹣x﹣1=0未知数的最高次数是3,不符合题意;
B:2x﹣1=5未知数的最高次数是1,不符合题意;
C:是分式方程,不符合题意;
D:x2﹣3x+1=0符合一元二次方程的定义;
故选:D.
3.(2023秋 晋城期末)某校准备组织红色研学活动,需要从晋西北会议旧址、国民师范革命活动旧址、太原解放纪念馆旧址、晋绥八分区旧址四个红色教育基地中任选一个前往研学,则选中晋西北会议旧址的概率为( )
A. B. C. D.
【解答】解:∵红色教育基地有4个,
∴选中晋西北会议旧址的概率为.
故选:D.
4.(2023秋 盂县期末)一元二次方程x2﹣4=4x的根的情况为( )
A.有两个相等的实数根 B.有两个不等的实数根
C.没有实数根 D.有一个实数根
【解答】解:∵x2﹣4=4x,
∴x2﹣4x﹣4=0,
∴Δ=(﹣4)2﹣4×(﹣4)×1=16+16=32>0,
∴原方程有两个不相等的实数根,
故选:B.
5.(2023秋 耒阳市校级期末)已知圆锥的母线长为2,底面半径为1,则该圆锥的侧面展开图的面积为( )
A. B.π C.2π D.4π
【解答】解:∵圆锥的底面圆半径为1,
∴圆锥的底面周长为:2π,
∴圆锥的侧面展开图扇形的弧长为2π,
∴圆锥的侧面积为:×2π×2=2π,
故选:C.
6.(2023秋 兖州区期末)如图,AB是半圆的直径,CD为半圆的弦,且CD∥AB,∠ACD=36°,则∠B等于( )
A.36° B.46° C.54° D.72°
【解答】解:∵CD∥AB,
∴∠BAC=∠ACD=36°,
∵AB是半圆的直径,
∴∠ACB=90°,
∴∠ABC=90°﹣∠BAC
=90°﹣36°
=54°;
故选:C.
7.(2023秋 和田地区期末)如图,AB是⊙O的直径,弦CD⊥AB于点E,OC=5cm,CD=8cm,则BE=( )cm.
A.5 B.4 C.3 D.2
【解答】解:∵AB是⊙O的直径,
∴OB=OC=5cm,
∵弦CD⊥AB,
∴CE=DE=4cm,
在Rt△OCE中,OC=5cm,
∴,
∴BE=OB﹣OE=5﹣3=2(cm).
故选:D.
8.(2023秋 白水县期末)如图,若一个正六边形的对角线AB的长为10,则正六边形外接圆的半径为( )
A.8 B.6 C.5 D.4
【解答】解:取对角线AB的中点O,
∵点A与点B关于点O对称,且顶点A与顶点B关于正六边形的中心对称,
∴点O是该正六边形的中心,
∴OA是该正六边形的半径,即该正六边形外接圆的半径,
∴AB=10,
∴OA=OB=AB=5,
故选:C.
9.(2023秋 东昌府区校级期末)某机械厂七月份生产零件100万个,第三季度生产零件392万个.设该厂八、九月份平均每月的增长率为x,那么x满足的方程是( )
A.100(1+x)2=392
B.100+100(1+x)2=392
C.100+100(1+x)+100(1+2x)=392
D.100+100(1+x)+100(1+x)2=392
【解答】解:设该厂八、九月份平均每月的增长率为x,
根据题意可列方程:100+100(1+x)+100(1+x)2=392,
故选:D.
二.填空题(共9小题)
10.(2024春 乳山市期末)如果所示的地板由15块方砖组成,每一块方砖除颜色外完全相同,小球自由滚动,随机停在黑色方砖的概率为 .
【解答】解:∵总面积为15块方砖的面积,其中黑色方砖有5个,
∴小球停在黑色方砖的概率为=,
故答案为:.
11.(2023秋 巩义市期末)如图是一个可以自由转动的质地均匀的转盘,被分成12个相同的小扇形.若把某些小扇形涂上红色,使转动的转盘停止时,指针指向红色的概率是,则涂上红色的小扇形有 2 个.
【解答】解:由题意得,涂上红色的小扇形有(个);
故答案为:2.
12.(2023秋 渭城区期末)测试中心分别从操作系统、硬件规格、屏幕尺寸、电池寿命四个项目对新投入市场的一款智能手机进行测评,这款手机的各项得分如下表:
测试项目 操作系统 硬件规格 屏幕尺寸 电池寿命
项目成绩/分 7 8 9 6
最后将四项成绩按3:3:2:2的比例计算综合成绩,则该手机的综合成绩为 7.5 分.
【解答】解:由题意知,该手机的综合成绩为(分).
故答案为:7.5.
13.(2023秋 蒙阴县期末)若x1,x2是一元二次方程x2+2x﹣k﹣1=0的两根,且x1x2=﹣3,则k的值为 2 .
【解答】解:∵x1,x2是一元二次方程x2+2x﹣k﹣1=0的两根,且x1x2=﹣3,
∴﹣k﹣1=﹣3,
∴k=2.
故答案为:2.
14.(2023秋 岚山区期末)数字下乡,农货上行,直播逐渐成为农户销售农产品的重要渠道,某地农村网商2021年为1500家,2023年达到2160家,设2021年到2023年农村网商的月平均增长率为x,根据题意可列方程为 1500(x+1)2=2160 .
【解答】解:设2021年到2023年农村网商的月平均增长率为x,
由题意得,1500(1+x)2=2160,
故答案为:1500(1+x)2=2160.
15.(2023秋 电白区期末)如图,是一个长为30m,宽为20m的矩形花园,现要在花园中修建等宽的小道,剩余的地方种植花草.如图所示,要使种植花草的面积为532m2,那么小道进出口的宽度应为 1 米.
【解答】解:设小道进出口的宽度为x米,依题意得(30﹣2x)(20﹣x)=532,
整理,得x2﹣35x+34=0.
解得,x1=1,x2=34.
∵34>30(不合题意,舍去),
∴x=1.
答:小道进出口的宽度应为1米.
故答案为:1.
16.(2023秋 广饶县期末)如图,点A,B,C在半径为2的⊙O上,若∠BAC=30°,则弦BC= 2 .
【解答】解:∵∠BAC=30°,OB=OC=2,
∴∠BOC=2∠A=2×30°=60°,
∵OB=OC,
∴△OBC为等边三角形,
∴BC=OB=2,
故答案为:2.
17.(2023秋 陇县期末)如图,A,B,C为⊙O上的三点,∠AOB=4∠BOC,若∠ACB=60°,则∠BAC的度数是 15° .
【解答】解;∵∠ACB=60°,
∴∠AOB=2∠ACB=120°,
∵∠AOB=4∠BOC,
∴∠BOC=30°,
∴,
故答案为:15°.
18.(2023秋 东昌府区校级期末)如图,若⊙O的半径为1,则⊙O的内接正八边形AEBFCGDH的面积为 .
【解答】解:连接AC,OD,OH,
∵四边形ABCD是圆内接正四边形,∠ADC=90°,
∴AC是圆的直径,AC=2,
∵AD2+CD2=AC2,
∴,
∵DH=AH,
∴弧DH=弧AH,
∴OH⊥AD,
∴,
故答案为:.
三.解答题(共8小题)
19.(2023秋 平定县期末)解方程.
(1)3x2﹣2x﹣7=0.
(2)(2x+1)(5x﹣3)=﹣2(3﹣5x).
【解答】解:(1)3x2﹣2x﹣7=0,
a=3,b=﹣2,c=﹣7,
Δ=b2﹣4ac=4+84=88>0,
∴方程有两个不相等的实数根.
,
∴,.
(2)(2x+1)(5x﹣3)=﹣2(3﹣5x),
方程可变形为(2x+1)(5x﹣3)﹣2(5x﹣3)=0,
因式分解,得(2x﹣1)(5x﹣3)=0,
所以得2x﹣1=0,或5x﹣3=0,
∴,.
20.(2024春 阳山县期末)一个不透明的袋中装有18个白球和若干个红球,它们除颜色外其他均相同.已知将袋中球摇匀后,从中任意摸出一个球是白球的概率是.
(1)求袋中总共有多少个球?
(2)从袋中取走10个球(其中没有红球)并将袋中球摇匀后,求从剩余的球中任意摸出一个球是红球的概率.
【解答】解:(1)设袋中总共有x个球,
∵袋中装有18个白球,从中任意摸出一个球是白球的概率是,
∴=,
解得x=30,
经检验,x=30是原方程的解,
即袋中总共有30个球;
(2)袋子中红球的个数为:30﹣18=12(个),
取走10个球,则袋子中球的总个数为30﹣10=20(个),
∴剩余的球中任意摸出一个球是红球的概率为=.
21.(2023秋 曹县期末)某商场2023年九月份的销售额为200万元,十月份的销售额下降了20%,商场从十一月份起加强管理,改善经营,使销售额稳步上升,十二月份的销售额达到了193.6万元,若十一月、十二月销售额增长的百分率相同,求十一月份的销售额是多少万元?
【解答】解:设十一月、十二月销售额增长的百分率为x,
根据题意,得200×(1﹣20%)(1+x)2=193.6,
解这个方程,得x1=0.1=10%,x2=﹣2.1(不合题意,舍去),
∴200×(1﹣20%)×(1+10%)=176(万元).
答:十一月份的销售额为176万元.
22.(2023秋 宿城区期末)2022年3月25日,教育部印发《义务教育课程方案和课程标准(2022年版)》,优化了课程设置,将劳动从综合实践活动课程中独立出来.某校为了解该校学生一周的课外劳动情况,随机抽取部分学生调查了他们一周的课外劳动时间,将数据进行整理并制成如一统计图.
请根据图中提供的信息,解答下列的问题:
(1)求图1中的m= 25 ,本次调查数据的中位数是 3 h,本次调查数据的众数是 3 h;
(2)若该校共有2000名学生,请根据统计数据,估计该校学生一周的课外劳动时间不小于3h的人数.
【解答】解:(1)4÷10%=40人,
∴参与调查的学生人数为40人,
∴,
∴m=25,
∵参与调查的学生人数一共有40人,将他们的劳动时间从低到高排列,处在第20名和第21名的劳动时间分别为3h,3h
∴中位数为,
由条形统计图可知,劳动时间为3h的人数最多,
∴众数为3h,
故答案为:25,3,3;
(2)解:(人),
答:估计该校学生一周的课外劳动时间不小于3h的人数为1400人.
23.(2023秋 嵩明县期末)某校为贯彻落实教育部《关于全面加强中小学生劳动教育的意见》,更好地培养学生的劳动兴趣和劳动技能,计划在校园开辟一块劳动教育基地,一面利用学校的墙(墙的长度为16m),用30m长的篱笆,围成一个如图所示的矩形菜地ABCD,供同学们进行劳动实践.
(1)若围成的菜地面积为100m2,求此时AB的长.
(2)能围成面积为120m2的菜地吗?若能,请求出AB的值;若不能,请说明理由.
【解答】解:(1)设AB的长为x米,则BC的长为(30﹣2x)米,
根据题意得:x(30﹣2x)=100,
整理得:x2﹣15x+50=0,
解得:x1=5,x2=10,
当x=5时,30﹣2x=30﹣2×5=20>16,不符合题意,舍去;
当x=10时,30﹣2x=30﹣2×10=10<16,符合题意.
答:AB的长为10米;
(2)不能围成面积为120m2的菜地,理由入下:
假设能围成面积为120m2的菜地,设AB的长为y米,则BC的长为(30﹣2y)米,
根据题意得:y(30﹣2y)=120,
整理得:y2﹣15y+60=0,
∵Δ=152﹣4×1×60=﹣15<0,
∴原方程没有实数根,
∴假设不成立,即不能围成面积为120m的菜地.
24.(2023秋 准格尔旗期末)如图,AB为⊙O的直径,CB,CD分别切⊙O于点B,D,CD交BA的延长线于点E,CO的延长线交⊙O于点G,EF⊥OG于点F.
(1)求证:∠FEB=∠ECF;
(2)若BC=6,DE=4,求线段OE的长.
【解答】(1)证明:∵CB,CD分别切⊙O于点B,D,
∴OC平分∠BCE,即∠ECO=∠BCO,OB⊥BC,
∴∠BCO+∠COB=90°,
∵EF⊥OG,
∴∠FEB+∠FOE=90°,
而∠COB=∠FOE,
∴∠FEB=∠ECF;
(2)解:连接OD,如图,
∵CB,CD分别切⊙O于点B,D,
∴CD=CB=6,OD⊥CE,
∴CE=CD+DE=6+4=10,
在Rt△BCE中,,
设⊙O的半径为r,则OD=OB=r,OE=8﹣r,
在Rt△ODE中,r2+42=(8﹣r)2,
解得r=3,
∴OE=8﹣3=5.
25.(2022秋 玉林期末)如图,AB是⊙O的直径,点C是⊙O上的一点,CD与AB的延长线交于点D,已知:CA=CD,∠A=30°.
(1)求证:CD是⊙O的切线;
(2)过点B作BE⊥CD于点E,若⊙O的半径为2,求图中阴影部分的面积.
【解答】(1)证明:连接OC,
∵OA=OC,
∴∠OCA=∠A=30°,
∴∠COD=60°,
又CA=CD,
∴∠D=∠A=30°,
∴∠OCD=180°﹣60°﹣30°=90°,
∴半径OC⊥CD,
∴CD是⊙O的切线;
(2)解:∵OC=2,∠A=∠D=30°,∠OCD=90°,
∴OD=2OC=4,
又OB=2,
∴BD=OB=2,即点B是OD的中点,
又∵BE⊥CD,
∴BE∥OC,BE是△OCD的中位线,
∴,
∴,
∴S阴=S梯形OBEC﹣S扇形OBC
=
=.
26.(2023秋 东莞市校级期末)HUAWEIMate60Pro是华为技术有限公司于2023年8月29日上架的一款全球首款支持卫星通话的大众智能手机,即使在没有地面网络信号的情况下,也可以拨打接听卫星电话,该手机还支持AI隔空操控、智感支付、注视不熄屏等智慧功能等.该系列完成了核心技术领域从0到1的跃迁,让无数国人为之自豪并被赞誉为“争气机”.手机背面有一条圆弧,象征着以山河之美致敬奔腾不息的力量.如图,圆弧对应的弦AB长80mm,半径OC⊥AB,垂足为D,弓形高CD长14mm.
(1)求AD的长;
(2)求半径OA的长.
【解答】解:(1)∵OC⊥AB,AB=80mm,
∴;
(2)∵OC⊥AB,
∴∠ADO=90°,
设半径OA=x mm,则OC=OA=x mm,OD=OC﹣CD=(x﹣14)mm,
∴AD2+OD2=OA2,
402+(x﹣14)2=x2,
1600+x2﹣28x+196=x2,
28x=1796,
,
∴半径OA的长为.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
