2024-2025学年人教版九年级上册数学期末试题重组练习(含解析)
文档属性
| 名称 | 2024-2025学年人教版九年级上册数学期末试题重组练习(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 964.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-10 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
2024-2025学年人教版九年级上册数学期末试题重组练习
一.选择题(共10小题)
1.(2023 恩施市校级期末)下列4个图形中,是中心对称图形的是( )
A. B. C. D.
2.(2023 连州市期末)如果方程mx2﹣6x+1=0有实数根,那么m的取值范围是( )
A.m<9且m≠0 B.m≤9且m≠0 C.m<9 D.m≤9
3.(2023秋 柳北区期末)下列函数属于二次函数的是( )
A.y=2x B.y=2x2﹣1 C. D.y=x﹣2+1
4.(2023 东海县模拟)下列语句中不正确的有( )
①相等的圆心角所对的弧相等;
②平分弦的直径垂直于弦;
③圆是轴对称图形,任何一条直径都是它的对称轴;
④半圆是弧.
A.1个 B.2个 C.3个 D.4个
5.(2023秋 龙口市期末)将二次函数y=(x+1)2的图象向上平移2个单位,得到的图象对应的函数表达式是( )
A.y=(x+3)2 B.y=(x﹣1)2
C.y=(x+1)2﹣2 D.y=(x+1)2+2
6.(2023秋 麻章区校级期末)下列说法正确的是( )
A.“清明时节雨纷纷”是必然事件
B.为了了解某小区居民新冠疫苗注射情况,可以采用全面调查方式进行
C.一组数据2,5,4,5,6,7的众数、中位数和平均数都是4.5
D.甲、乙两组队员身高数据的方差分别为,,那么甲组队员身高比较整齐
7.(2023秋 长子县期末)某大型连锁超市以17元/斤的价格购进草莓1万斤,在运输、储存过程中部分草莓损坏,超市管理员从所有的草莓中随机抽取了若干进行“草莓损坏率”统计,并把获得的数据记录如表:
草莓总质量n/斤 20 50 100 200 500
损坏草莓质量m/斤 3.12 7.7 15.2 29.8 75
草莓损坏的频率 0.156 0.154 0.152 0.149 0.150
超市管理员希望卖出草莓(损坏的草莓不能出售)可以获得利润42500元,那么就需要利用草莓损坏的概率(精确到0.01)估算草莓的售价.根据表中数据可以估计,草莓每斤的售价应该定为( )
A.25元 B.22元 C.21.25元 D.21.5元
8.(2023秋 广饶县期末)如图,AB是⊙O的直径,∠ACD=15°,则∠BAD的度数为( )
A.75° B.65° C.60° D.85°
9.(2023秋 鼓楼区校级期末)近年来,我国数字技术不断革新,影响着全民阅读形态.为预计某市2023年数字阅读市场规模,经查询得数据:该市2021年数字阅读市场规模为432万元,2023年数字阅读市场规模为507万元.设该市年平均增长率为x,则下列方程正确的是( )
A.432(1+2x)=507
B.432(1+2x)2=507
C.432(1+x)2=507
D.432+432(1+x)+432(1+x)2=507
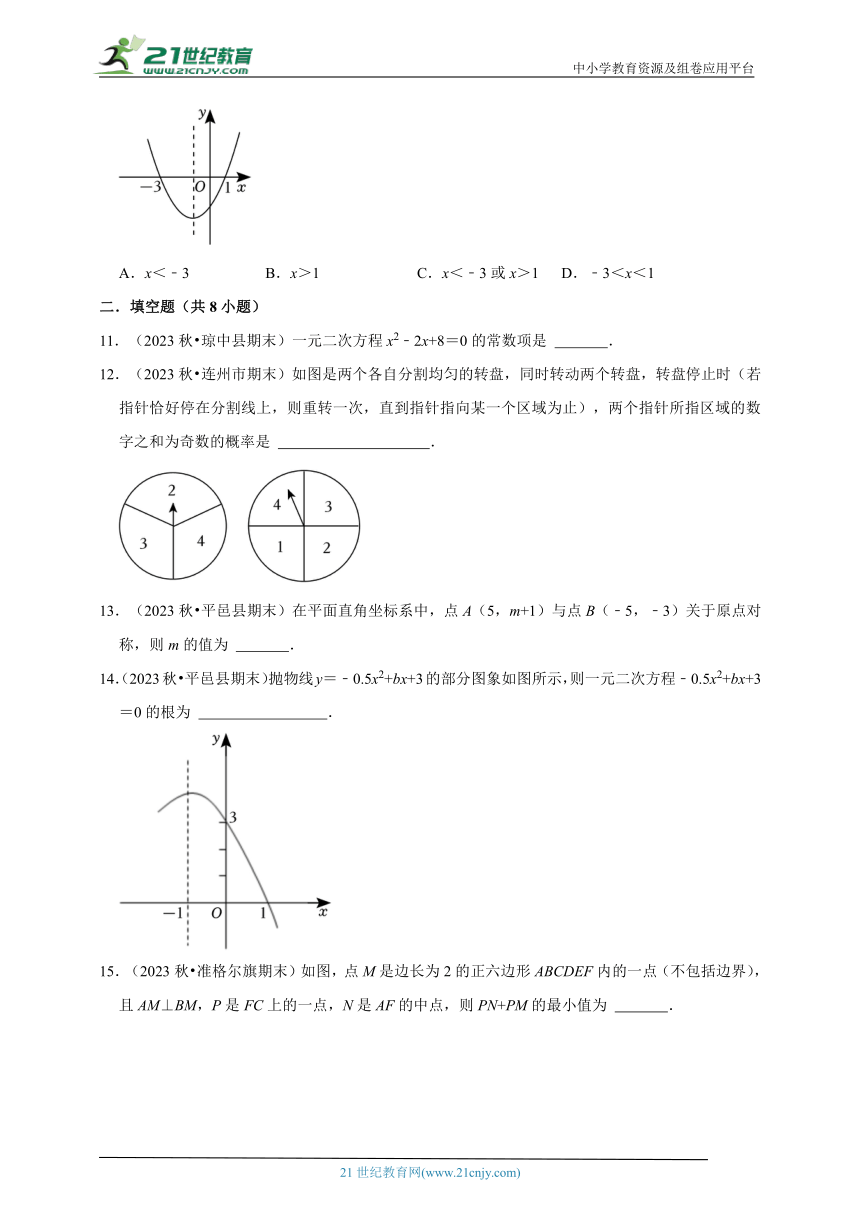
10.(2023秋 陇西县期末)二次函数y=ax2+bx+c(a≠0)的图象如图所示,当y<0时自变量x的取值范围是( )
A.x<﹣3 B.x>1 C.x<﹣3或x>1 D.﹣3<x<1
二.填空题(共8小题)
11.(2023秋 琼中县期末)一元二次方程x2﹣2x+8=0的常数项是 .
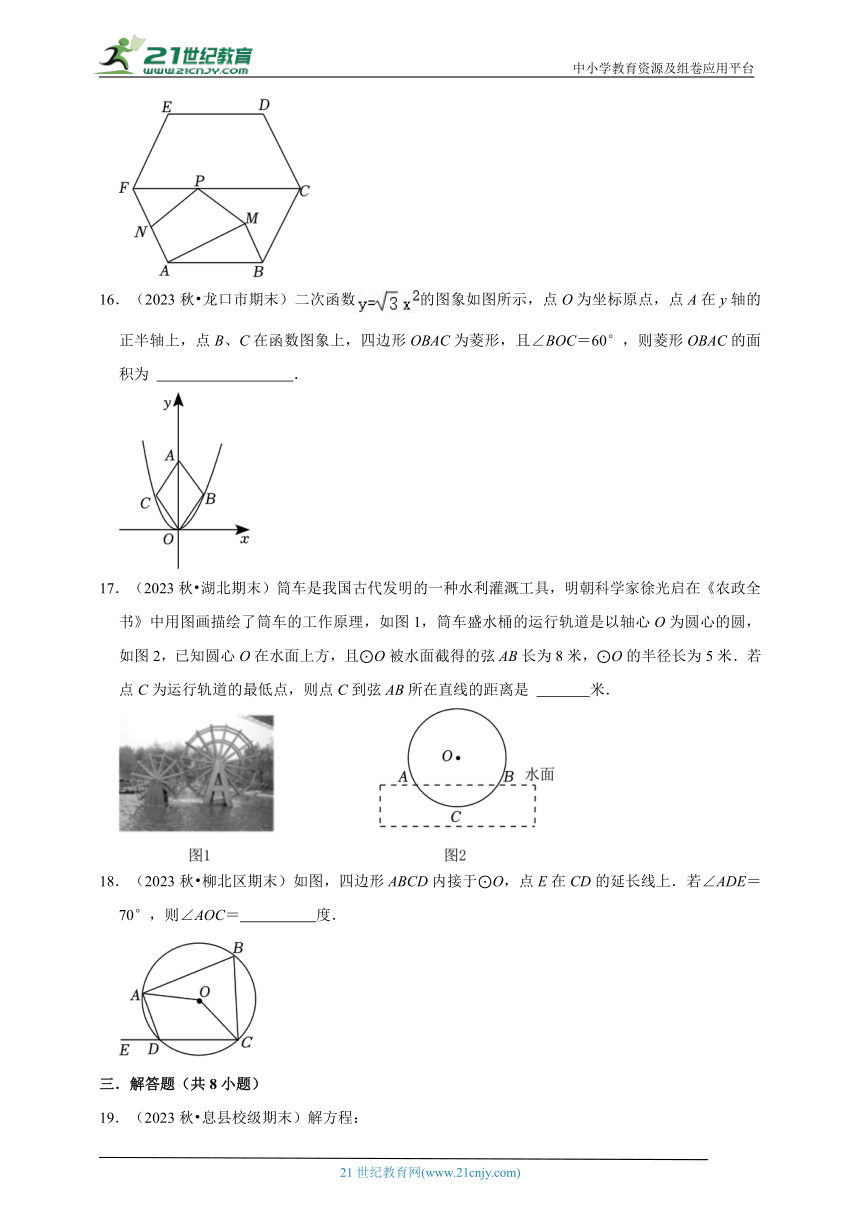
12.(2023秋 连州市期末)如图是两个各自分割均匀的转盘,同时转动两个转盘,转盘停止时(若指针恰好停在分割线上,则重转一次,直到指针指向某一个区域为止),两个指针所指区域的数字之和为奇数的概率是 .
13.(2023秋 平邑县期末)在平面直角坐标系中,点A(5,m+1)与点B(﹣5,﹣3)关于原点对称,则m的值为 .
14.(2023秋 平邑县期末)抛物线y=﹣0.5x2+bx+3的部分图象如图所示,则一元二次方程﹣0.5x2+bx+3=0的根为 .
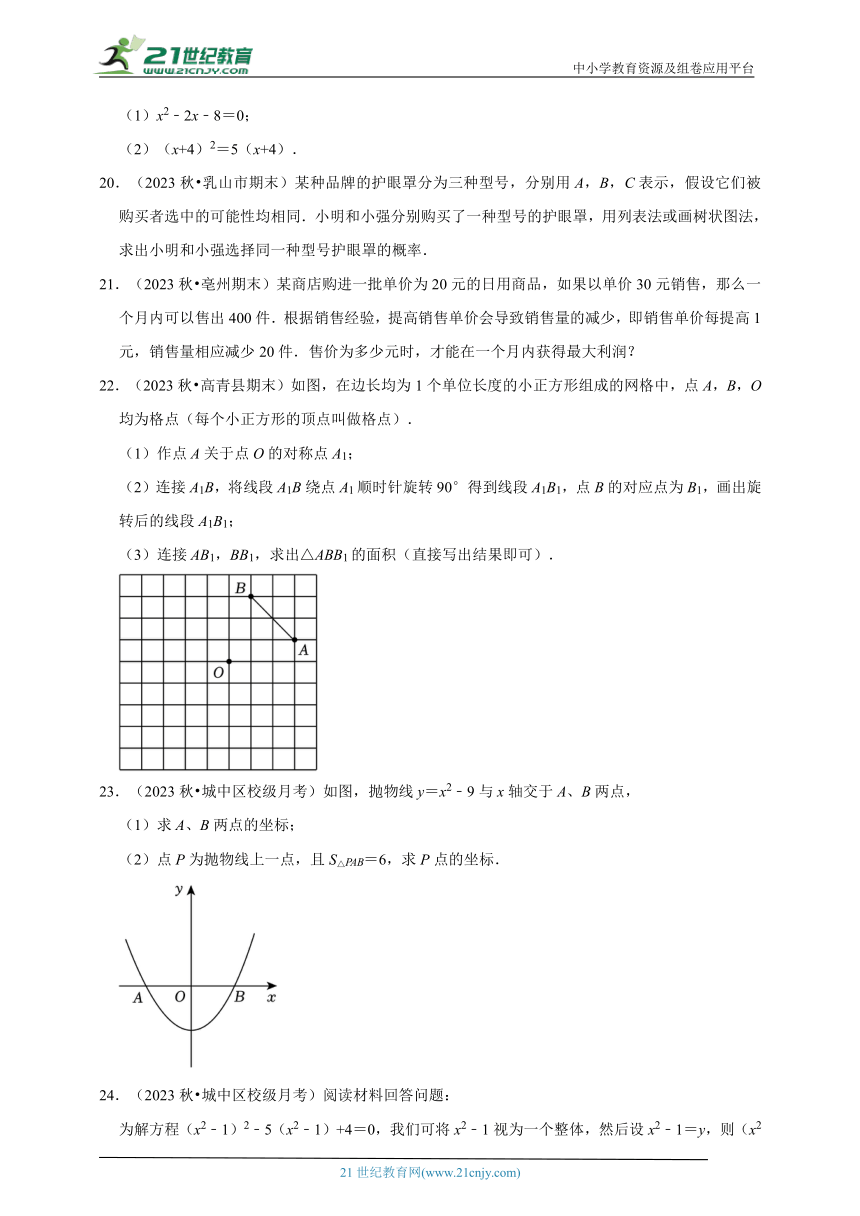
15.(2023秋 准格尔旗期末)如图,点M是边长为2的正六边形ABCDEF内的一点(不包括边界),且AM⊥BM,P是FC上的一点,N是AF的中点,则PN+PM的最小值为 .
16.(2023秋 龙口市期末)二次函数的图象如图所示,点O为坐标原点,点A在y轴的正半轴上,点B、C在函数图象上,四边形OBAC为菱形,且∠BOC=60°,则菱形OBAC的面积为 .
17.(2023秋 湖北期末)筒车是我国古代发明的一种水利灌溉工具,明朝科学家徐光启在《农政全书》中用图画描绘了筒车的工作原理,如图1,筒车盛水桶的运行轨道是以轴心O为圆心的圆,如图2,已知圆心O在水面上方,且⊙O被水面截得的弦AB长为8米,⊙O的半径长为5米.若点C为运行轨道的最低点,则点C到弦AB所在直线的距离是 米.
18.(2023秋 柳北区期末)如图,四边形ABCD内接于⊙O,点E在CD的延长线上.若∠ADE=70°,则∠AOC= 度.
三.解答题(共8小题)
19.(2023秋 息县校级期末)解方程:
(1)x2﹣2x﹣8=0;
(2)(x+4)2=5(x+4).
20.(2023秋 乳山市期末)某种品牌的护眼罩分为三种型号,分别用A,B,C表示,假设它们被购买者选中的可能性均相同.小明和小强分别购买了一种型号的护眼罩,用列表法或画树状图法,求出小明和小强选择同一种型号护眼罩的概率.
21.(2023秋 亳州期末)某商店购进一批单价为20元的日用商品,如果以单价30元销售,那么一个月内可以售出400件.根据销售经验,提高销售单价会导致销售量的减少,即销售单价每提高1元,销售量相应减少20件.售价为多少元时,才能在一个月内获得最大利润?
22.(2023秋 高青县期末)如图,在边长均为1个单位长度的小正方形组成的网格中,点A,B,O均为格点(每个小正方形的顶点叫做格点).
(1)作点A关于点O的对称点A1;
(2)连接A1B,将线段A1B绕点A1顺时针旋转90°得到线段A1B1,点B的对应点为B1,画出旋转后的线段A1B1;
(3)连接AB1,BB1,求出△ABB1的面积(直接写出结果即可).
23.(2023秋 城中区校级月考)如图,抛物线y=x2﹣9与x轴交于A、B两点,
(1)求A、B两点的坐标;
(2)点P为抛物线上一点,且S△PAB=6,求P点的坐标.
24.(2023秋 城中区校级月考)阅读材料回答问题:
为解方程(x2﹣1)2﹣5(x2﹣1)+4=0,我们可将x2﹣1视为一个整体,然后设x2﹣1=y,则(x2﹣1)2=y2,原方程可化为y2﹣5y+4=0①.
解得y1=1,y2=4,当y=1时,x2﹣1=1,所以x2=2,x=±;
当y=4时,x2﹣1=4,所以x2=5,x=±;
所以原方程的解为,x2=﹣,x1=,x2=﹣y.
解方程:(x2+1)2+4(x2+1)﹣12=0.
25.(2023秋 天津月考)如图,抛物线y=ax2+bx+3(a<0)与x轴交于A(﹣1,0),B两点,与y轴交于点C,对称轴为直线x=1.
(1)直接写出抛物线的解析式;
(2)P是抛物线上一动点(不与点C重合),直线CP交对称轴于点AN,连接AN,当∠ANC=45°时,求直线PC的解析式.
26.(2023秋 鼓楼区校级期末)如图,△ABC中,AB=AC,点O是底边BC的中点,腰AB与⊙O相切于点D.
(1)求证:AC是⊙O的切线;
(2)若⊙O的半径为2,∠C=45°,求图中阴影部分的面积.
2024-2025学年人教版九年级上册数学期末试题重组练习
参考答案与试题解析
题号 1 2 3 4 5 6 7 8 9 10
答案 B D B C D B A A C D
一.选择题(共10小题)
1.(2023 恩施市校级期末)下列4个图形中,是中心对称图形的是( )
A. B. C. D.
【解答】解:选项A、C、D的图形都不能找到一个点,使这些图形绕某一点旋转180°与原来的图形重合,所以不是中心对称图形;
选项B的图形能找到一个点,使这个图形绕某一点旋转180°与原来的图形重合,所以是中心对称图形;
故选:B.
2.(2023 连州市期末)如果方程mx2﹣6x+1=0有实数根,那么m的取值范围是( )
A.m<9且m≠0 B.m≤9且m≠0 C.m<9 D.m≤9
【解答】解:∵关于x的方程mx2﹣6x+1=0有实数根,
∴当方程是一元二次方程时,Δ=(﹣6)2﹣4m≥0,
解得:m≤9,且m≠0;
当方程是一元一次方程时,则m=0,
故选:D.
3.(2023秋 柳北区期末)下列函数属于二次函数的是( )
A.y=2x B.y=2x2﹣1 C. D.y=x﹣2+1
【解答】解:A、y=2x是一次函数,不是二次函数;
B、y=2x2﹣1是二次函数;
C、不是二次函数;
D、y=x﹣2+1不是二次函数;
故选:B.
4.(2023 东海县模拟)下列语句中不正确的有( )
①相等的圆心角所对的弧相等;
②平分弦的直径垂直于弦;
③圆是轴对称图形,任何一条直径都是它的对称轴;
④半圆是弧.
A.1个 B.2个 C.3个 D.4个
【解答】解:①、要强调在同圆或等圆中相等的圆心角所对的弧相等;故错误.
②、平分弦的直径垂直于弦,其中被平分的弦不能是直径,若是直径则错误.
③、对称轴是直线,而直径是线段,故错误.
④、正确.
故选:C.
5.(2023秋 龙口市期末)将二次函数y=(x+1)2的图象向上平移2个单位,得到的图象对应的函数表达式是( )
A.y=(x+3)2 B.y=(x﹣1)2
C.y=(x+1)2﹣2 D.y=(x+1)2+2
【解答】解:由题可知,二次函数y=(x+1)2的图象向上平移了2个单位,根据规律可得出平移后的函数表达式为y=(x+1)2+2.
故选:D.
6.(2023秋 麻章区校级期末)下列说法正确的是( )
A.“清明时节雨纷纷”是必然事件
B.为了了解某小区居民新冠疫苗注射情况,可以采用全面调查方式进行
C.一组数据2,5,4,5,6,7的众数、中位数和平均数都是4.5
D.甲、乙两组队员身高数据的方差分别为,,那么甲组队员身高比较整齐
【解答】解:A.“清明时节雨纷纷”是随机事件,原说法错误,不符合题意;
B.为了了解某小区居民新冠疫苗注射情况,可以采用全面调查方式进行,正确,符合题意
C.一组数据2,5,4,5,6,7的众数是5,中位数是5,平均数是,原说法错误,不符合题意;
D.甲、乙两组队员身高数据的方差分别为,,那么乙队员身高比较整齐,原说法错误,不符合题意,
故选:B.
7.(2023秋 长子县期末)某大型连锁超市以17元/斤的价格购进草莓1万斤,在运输、储存过程中部分草莓损坏,超市管理员从所有的草莓中随机抽取了若干进行“草莓损坏率”统计,并把获得的数据记录如表:
草莓总质量n/斤 20 50 100 200 500
损坏草莓质量m/斤 3.12 7.7 15.2 29.8 75
草莓损坏的频率 0.156 0.154 0.152 0.149 0.150
超市管理员希望卖出草莓(损坏的草莓不能出售)可以获得利润42500元,那么就需要利用草莓损坏的概率(精确到0.01)估算草莓的售价.根据表中数据可以估计,草莓每斤的售价应该定为( )
A.25元 B.22元 C.21.25元 D.21.5元
【解答】解:由表格中的数据可得草莓的损坏率大约为15%,
则完好率为:1﹣15%=85%,
设每斤草莓的售价为x元,根据题意得,
10000×x×85%﹣10000×17=42500,
解得,x=25,
即每斤草莓的售价为25元,
故选:A.
8.(2023秋 广饶县期末)如图,AB是⊙O的直径,∠ACD=15°,则∠BAD的度数为( )
A.75° B.65° C.60° D.85°
【解答】解:连接BD,
∵AB是⊙O的直径,
∴∠ADB=90°,
又∵∠C=∠B=15°,
∴∠BAD=90°﹣∠B=90°﹣15°=75°,
故选:A.
9.(2023秋 鼓楼区校级期末)近年来,我国数字技术不断革新,影响着全民阅读形态.为预计某市2023年数字阅读市场规模,经查询得数据:该市2021年数字阅读市场规模为432万元,2023年数字阅读市场规模为507万元.设该市年平均增长率为x,则下列方程正确的是( )
A.432(1+2x)=507
B.432(1+2x)2=507
C.432(1+x)2=507
D.432+432(1+x)+432(1+x)2=507
【解答】解:根据题意得:432(1+x)2=507.
故选:C.
10.(2023秋 陇西县期末)二次函数y=ax2+bx+c(a≠0)的图象如图所示,当y<0时自变量x的取值范围是( )
A.x<﹣3 B.x>1 C.x<﹣3或x>1 D.﹣3<x<1
【解答】解:由图可知,﹣3<x<1时,y<0.
故选:D.
二.填空题(共8小题)
11.(2023秋 琼中县期末)一元二次方程x2﹣2x+8=0的常数项是 8 .
【解答】解:一元二次方程x2﹣2x+8=0的常数项是8.
故答案为:8.
12.(2023秋 连州市期末)如图是两个各自分割均匀的转盘,同时转动两个转盘,转盘停止时(若指针恰好停在分割线上,则重转一次,直到指针指向某一个区域为止),两个指针所指区域的数字之和为奇数的概率是 .
【解答】解:列表如下:
1 2 3 4
2 (2,1) (2,2) (2,3) (2,4)
3 (3,1) (3,2) (3,3) (3,4)
4 (4,1) (4,2) (4,3) (4,4)
共有12种等可能的结果,其中两个指针所指区域的数字之和为奇数的结果有:(2,1),(2,3),(3,2),(3,4),(4,1),(4,3),共6种,
∴两个指针所指区域的数字之和为奇数的概率为.
故答案为:.
13.(2023秋 平邑县期末)在平面直角坐标系中,点A(5,m+1)与点B(﹣5,﹣3)关于原点对称,则m的值为 2 .
【解答】解:∵点A(5,m+1)与点B(﹣5,﹣3)关于原点对称,
∴m+1=3,
解得:m=2.
故答案为:2.
14.(2023秋 平邑县期末)抛物线y=﹣0.5x2+bx+3的部分图象如图所示,则一元二次方程﹣0.5x2+bx+3=0的根为 x1=1,x2=﹣3 .
【解答】解:由图象得:抛物线y=﹣0.5x2+bx+3与x轴的一个交点为(1,0),且对称轴为直线x=﹣1,
∴抛物线y=﹣0.5x2+bx+3与x轴的另一个交点为(﹣3,0),
故一元二次方程﹣0.5x2+bx+3=0的根为:x1=1,x2=﹣3,
故答案为:x1=1,x2=﹣3.
15.(2023秋 准格尔旗期末)如图,点M是边长为2的正六边形ABCDEF内的一点(不包括边界),且AM⊥BM,P是FC上的一点,N是AF的中点,则PN+PM的最小值为 2 .
【解答】解:取AB中点O,EF中点Q,连接PQ,MO,延长EF、BA相交于点T,
,
∵正六边形ABCDEF关于直线CF对称,
∴N,Q也关于直线CF对称,
∴PQ=PN,
∵AM⊥BM,O为AB中点,
∴,
∴PN+PM+MO=PQ+PM+MO≥QO,
当Q,P,M,O共线时,PN+PM+MO=PQ+PM+MO=QO,
∴PN+PM的最小值为QO﹣MO=QM,
∵正六边形ABCDEF的边长为2,
∴,AF=EF=AB=2,
∴△TAF是等边三角形,
∴FT=AT,∠T=60°,
∵EF=AB=2,O为AB中点,Q为EF中点,
∴,,
∴TQ=3=TO,
∴△TQO是等边三角形,
∴QO=3,
∴QM=2,
∴PN+PM的最小值为2.
故答案为:2.
16.(2023秋 龙口市期末)二次函数的图象如图所示,点O为坐标原点,点A在y轴的正半轴上,点B、C在函数图象上,四边形OBAC为菱形,且∠BOC=60°,则菱形OBAC的面积为 .
【解答】解:连接BC交OA于D,如图,
∵四边形OBAC为菱形,
∴BC⊥OA,
∵∠BOC=60°,
∴∠BOD=30°,
∴,
设BD=t,则,
∴,
把代入,
得,
解得t1=0(舍去),t2=1,
∴BD=1,,
∴BC=2,,
∴菱形OBAC的面积为:,
故答案为:.
17.(2023秋 湖北期末)筒车是我国古代发明的一种水利灌溉工具,明朝科学家徐光启在《农政全书》中用图画描绘了筒车的工作原理,如图1,筒车盛水桶的运行轨道是以轴心O为圆心的圆,如图2,已知圆心O在水面上方,且⊙O被水面截得的弦AB长为8米,⊙O的半径长为5米.若点C为运行轨道的最低点,则点C到弦AB所在直线的距离是 2 米.
【解答】解:如下图所示,连接OA、OC,
∵OC交AB于点E,则有OE⊥AB,
∴(米),
又∵OA=OC=5米,
在Rt△AOE中,(米),
∴CE=CO﹣OE=5﹣3=2(米),
答:若点C为运行轨道的最低点,则点C到弦AB所在直线的距离是2米.
故答案为:2.
18.(2023秋 柳北区期末)如图,四边形ABCD内接于⊙O,点E在CD的延长线上.若∠ADE=70°,则∠AOC= 140 度.
【解答】解:∵∠ADE=70°,
∴∠ADC=180°﹣∠ADE=180°﹣70°=110°,
∵四边形ABCD内接于⊙O,
∴∠ABC+∠ADC=180°,
∴∠ABC=180°﹣110°=70°,
由圆周角定理得:∠AOC=2∠ABC=140°,
故答案为:140.
三.解答题(共8小题)
19.(2023秋 息县校级期末)解方程:
(1)x2﹣2x﹣8=0;
(2)(x+4)2=5(x+4).
【解答】解:(1)x2﹣2x﹣8=0.
(x﹣4)(x+2)=0,
(x﹣4)=0,(x+2)=0,
∴x1=4,x2=﹣2;
(2)(x+4)2﹣5(x+4)=0,
(x+4)(x+4﹣5)=0,
∴x+4=0或x﹣1=0,
∴x1=﹣4,x2=1.
20.(2023秋 乳山市期末)某种品牌的护眼罩分为三种型号,分别用A,B,C表示,假设它们被购买者选中的可能性均相同.小明和小强分别购买了一种型号的护眼罩,用列表法或画树状图法,求出小明和小强选择同一种型号护眼罩的概率.
【解答】解:树状图如下所示,
由上可得,共有9种等可能结果,小明和小强选择同一种型号护眼罩有3种结果.
∴P(同一种型号)=,
即小明和小强选择同一种型号护眼罩的概率是.
21.(2023秋 亳州期末)某商店购进一批单价为20元的日用商品,如果以单价30元销售,那么一个月内可以售出400件.根据销售经验,提高销售单价会导致销售量的减少,即销售单价每提高1元,销售量相应减少20件.售价为多少元时,才能在一个月内获得最大利润?
【解答】解:设销售单价为x元,销售利润为y元.
根据题意,得:
y=(x﹣20)[400﹣20(x﹣30)]
=(x﹣20)(1000﹣20x)
=﹣20x2+1400x﹣20000
=﹣20(x﹣35)2+4500,
∵﹣20<0,
∴x=35时,y有最大值.
所以,销售单价为35元,才能在一个月内获得最大利润.
22.(2023秋 高青县期末)如图,在边长均为1个单位长度的小正方形组成的网格中,点A,B,O均为格点(每个小正方形的顶点叫做格点).
(1)作点A关于点O的对称点A1;
(2)连接A1B,将线段A1B绕点A1顺时针旋转90°得到线段A1B1,点B的对应点为B1,画出旋转后的线段A1B1;
(3)连接AB1,BB1,求出△ABB1的面积(直接写出结果即可).
【解答】解:(1)如图所示,点A1即为所求;
(2)如图所示,线段A1B1即为所求;
(3)如图,连接AB1,BB1,
则=×8×2=8.
23.(2023秋 城中区校级月考)如图,抛物线y=x2﹣9与x轴交于A、B两点,
(1)求A、B两点的坐标;
(2)点P为抛物线上一点,且S△PAB=6,求P点的坐标.
【解答】解:(1)抛物线y=x2﹣9,令y=0,得到x=3或﹣3,即A(﹣3,0),B(3,0);
(2)由点A、B的坐标可知:AB=6,
∵S△PAB=6,设P纵坐标为b,
∴×6|b|=6,即|b|=2,
∴b=2或﹣2,
当b=2时,x2﹣9=2,解得:x=±,此时P坐标为(,2),(﹣,2);
当b=﹣2时,x2﹣9=﹣2,解得:x=±,此时P坐标为(,﹣2),(﹣,﹣2),
综上,P的坐标为(,2)或(﹣,2)或(,﹣2)或(﹣,﹣2).
24.(2023秋 城中区校级月考)阅读材料回答问题:
为解方程(x2﹣1)2﹣5(x2﹣1)+4=0,我们可将x2﹣1视为一个整体,然后设x2﹣1=y,则(x2﹣1)2=y2,原方程可化为y2﹣5y+4=0①.
解得y1=1,y2=4,当y=1时,x2﹣1=1,所以x2=2,x=±;
当y=4时,x2﹣1=4,所以x2=5,x=±;
所以原方程的解为,x2=﹣,x1=,x2=﹣y.
解方程:(x2+1)2+4(x2+1)﹣12=0.
【解答】解:(x2+1)2+4(x2+1)﹣12=0,
设y=x2+1,
则原方程化为y2+4y﹣12=0,
(y+6)(y﹣2)=0,
∴y1=﹣6,y2=2,
∵y=x2+1>1,
∴y1=﹣6(舍去),
∴x2+1=2,
x2=1,
x1=1,x2=﹣1.
25.(2023秋 天津月考)如图,抛物线y=ax2+bx+3(a<0)与x轴交于A(﹣1,0),B两点,与y轴交于点C,对称轴为直线x=1.
(1)直接写出抛物线的解析式;
(2)P是抛物线上一动点(不与点C重合),直线CP交对称轴于点AN,连接AN,当∠ANC=45°时,求直线PC的解析式.
【解答】解:(1)根据题意得,即b=﹣2a,
∴y=ax2﹣2ax+3,
∵A(﹣1,0),
∴a+2a+3=0,
解得a=﹣1,
∴抛物线解析式为y=﹣x2+2x+3;
(2)如图所示,过点A作AM⊥AN交直线CP于M,过点M作MQ⊥x轴于Q,
设抛物线对称轴与x轴交点为D,
∴∠AQM=∠MAN=∠NDA=90°,D(1,0),
∴∠AMQ+∠MAQ=90°,
又∵∠MAQ+∠NAD=90°,
∴∠AMQ=∠NAD,
∴∠AMN=∠ANM=45°,
∴AM=NA,
∴△AMQ≌△NAD(AAS),
∴MQ=AD,AQ=ND,
设直线CP的解析式为y=kx+3,点N的坐标为(1,k+3),
∵当k+3>0时,A(﹣1,0),D(1,0),
∴MQ=AD=2,AQ=ND=k+3,
∴OQ=k+4,
∴点M的坐标为(﹣k﹣4,2),
∴k(﹣k﹣4)+3=2,即k2+4k﹣1=0,
解得或(舍去),
∴直线PC的解析式为,
同理可得当k+3≤0时,
解得y=﹣x+3.
综上所述,或y=﹣x+3.
26.(2023秋 鼓楼区校级期末)如图,△ABC中,AB=AC,点O是底边BC的中点,腰AB与⊙O相切于点D.
(1)求证:AC是⊙O的切线;
(2)若⊙O的半径为2,∠C=45°,求图中阴影部分的面积.
【解答】(1)证明:过点O作OG⊥AC于点G,连接AO,OD,
∵AB是⊙O的切线,
∴OD⊥AB,
∵点O是底边BC的中点,
∴OB=OC,
∵AB=AC,
∴AO平分∠BAC,AO⊥BC,
∴OD=OG,
∵OG是圆的半径,
∴AC是⊙O的切线;
(2)解:∵AB=AC,∠C=45°,
∴∠B=∠C=45°,
∴∠BAC=90°,即△BAC为等腰直角三角形,
∵∠ADO=∠AGO=90°,
∴四边形ADOG是矩形,
∵OD=OG,
∴四边形ADOG是正方形,
∴AD=OD=OG=AG=2,∠DOG=90°,
∴阴影部分的面积为.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024-2025学年人教版九年级上册数学期末试题重组练习
一.选择题(共10小题)
1.(2023 恩施市校级期末)下列4个图形中,是中心对称图形的是( )
A. B. C. D.
2.(2023 连州市期末)如果方程mx2﹣6x+1=0有实数根,那么m的取值范围是( )
A.m<9且m≠0 B.m≤9且m≠0 C.m<9 D.m≤9
3.(2023秋 柳北区期末)下列函数属于二次函数的是( )
A.y=2x B.y=2x2﹣1 C. D.y=x﹣2+1
4.(2023 东海县模拟)下列语句中不正确的有( )
①相等的圆心角所对的弧相等;
②平分弦的直径垂直于弦;
③圆是轴对称图形,任何一条直径都是它的对称轴;
④半圆是弧.
A.1个 B.2个 C.3个 D.4个
5.(2023秋 龙口市期末)将二次函数y=(x+1)2的图象向上平移2个单位,得到的图象对应的函数表达式是( )
A.y=(x+3)2 B.y=(x﹣1)2
C.y=(x+1)2﹣2 D.y=(x+1)2+2
6.(2023秋 麻章区校级期末)下列说法正确的是( )
A.“清明时节雨纷纷”是必然事件
B.为了了解某小区居民新冠疫苗注射情况,可以采用全面调查方式进行
C.一组数据2,5,4,5,6,7的众数、中位数和平均数都是4.5
D.甲、乙两组队员身高数据的方差分别为,,那么甲组队员身高比较整齐
7.(2023秋 长子县期末)某大型连锁超市以17元/斤的价格购进草莓1万斤,在运输、储存过程中部分草莓损坏,超市管理员从所有的草莓中随机抽取了若干进行“草莓损坏率”统计,并把获得的数据记录如表:
草莓总质量n/斤 20 50 100 200 500
损坏草莓质量m/斤 3.12 7.7 15.2 29.8 75
草莓损坏的频率 0.156 0.154 0.152 0.149 0.150
超市管理员希望卖出草莓(损坏的草莓不能出售)可以获得利润42500元,那么就需要利用草莓损坏的概率(精确到0.01)估算草莓的售价.根据表中数据可以估计,草莓每斤的售价应该定为( )
A.25元 B.22元 C.21.25元 D.21.5元
8.(2023秋 广饶县期末)如图,AB是⊙O的直径,∠ACD=15°,则∠BAD的度数为( )
A.75° B.65° C.60° D.85°
9.(2023秋 鼓楼区校级期末)近年来,我国数字技术不断革新,影响着全民阅读形态.为预计某市2023年数字阅读市场规模,经查询得数据:该市2021年数字阅读市场规模为432万元,2023年数字阅读市场规模为507万元.设该市年平均增长率为x,则下列方程正确的是( )
A.432(1+2x)=507
B.432(1+2x)2=507
C.432(1+x)2=507
D.432+432(1+x)+432(1+x)2=507
10.(2023秋 陇西县期末)二次函数y=ax2+bx+c(a≠0)的图象如图所示,当y<0时自变量x的取值范围是( )
A.x<﹣3 B.x>1 C.x<﹣3或x>1 D.﹣3<x<1
二.填空题(共8小题)
11.(2023秋 琼中县期末)一元二次方程x2﹣2x+8=0的常数项是 .
12.(2023秋 连州市期末)如图是两个各自分割均匀的转盘,同时转动两个转盘,转盘停止时(若指针恰好停在分割线上,则重转一次,直到指针指向某一个区域为止),两个指针所指区域的数字之和为奇数的概率是 .
13.(2023秋 平邑县期末)在平面直角坐标系中,点A(5,m+1)与点B(﹣5,﹣3)关于原点对称,则m的值为 .
14.(2023秋 平邑县期末)抛物线y=﹣0.5x2+bx+3的部分图象如图所示,则一元二次方程﹣0.5x2+bx+3=0的根为 .
15.(2023秋 准格尔旗期末)如图,点M是边长为2的正六边形ABCDEF内的一点(不包括边界),且AM⊥BM,P是FC上的一点,N是AF的中点,则PN+PM的最小值为 .
16.(2023秋 龙口市期末)二次函数的图象如图所示,点O为坐标原点,点A在y轴的正半轴上,点B、C在函数图象上,四边形OBAC为菱形,且∠BOC=60°,则菱形OBAC的面积为 .
17.(2023秋 湖北期末)筒车是我国古代发明的一种水利灌溉工具,明朝科学家徐光启在《农政全书》中用图画描绘了筒车的工作原理,如图1,筒车盛水桶的运行轨道是以轴心O为圆心的圆,如图2,已知圆心O在水面上方,且⊙O被水面截得的弦AB长为8米,⊙O的半径长为5米.若点C为运行轨道的最低点,则点C到弦AB所在直线的距离是 米.
18.(2023秋 柳北区期末)如图,四边形ABCD内接于⊙O,点E在CD的延长线上.若∠ADE=70°,则∠AOC= 度.
三.解答题(共8小题)
19.(2023秋 息县校级期末)解方程:
(1)x2﹣2x﹣8=0;
(2)(x+4)2=5(x+4).
20.(2023秋 乳山市期末)某种品牌的护眼罩分为三种型号,分别用A,B,C表示,假设它们被购买者选中的可能性均相同.小明和小强分别购买了一种型号的护眼罩,用列表法或画树状图法,求出小明和小强选择同一种型号护眼罩的概率.
21.(2023秋 亳州期末)某商店购进一批单价为20元的日用商品,如果以单价30元销售,那么一个月内可以售出400件.根据销售经验,提高销售单价会导致销售量的减少,即销售单价每提高1元,销售量相应减少20件.售价为多少元时,才能在一个月内获得最大利润?
22.(2023秋 高青县期末)如图,在边长均为1个单位长度的小正方形组成的网格中,点A,B,O均为格点(每个小正方形的顶点叫做格点).
(1)作点A关于点O的对称点A1;
(2)连接A1B,将线段A1B绕点A1顺时针旋转90°得到线段A1B1,点B的对应点为B1,画出旋转后的线段A1B1;
(3)连接AB1,BB1,求出△ABB1的面积(直接写出结果即可).
23.(2023秋 城中区校级月考)如图,抛物线y=x2﹣9与x轴交于A、B两点,
(1)求A、B两点的坐标;
(2)点P为抛物线上一点,且S△PAB=6,求P点的坐标.
24.(2023秋 城中区校级月考)阅读材料回答问题:
为解方程(x2﹣1)2﹣5(x2﹣1)+4=0,我们可将x2﹣1视为一个整体,然后设x2﹣1=y,则(x2﹣1)2=y2,原方程可化为y2﹣5y+4=0①.
解得y1=1,y2=4,当y=1时,x2﹣1=1,所以x2=2,x=±;
当y=4时,x2﹣1=4,所以x2=5,x=±;
所以原方程的解为,x2=﹣,x1=,x2=﹣y.
解方程:(x2+1)2+4(x2+1)﹣12=0.
25.(2023秋 天津月考)如图,抛物线y=ax2+bx+3(a<0)与x轴交于A(﹣1,0),B两点,与y轴交于点C,对称轴为直线x=1.
(1)直接写出抛物线的解析式;
(2)P是抛物线上一动点(不与点C重合),直线CP交对称轴于点AN,连接AN,当∠ANC=45°时,求直线PC的解析式.
26.(2023秋 鼓楼区校级期末)如图,△ABC中,AB=AC,点O是底边BC的中点,腰AB与⊙O相切于点D.
(1)求证:AC是⊙O的切线;
(2)若⊙O的半径为2,∠C=45°,求图中阴影部分的面积.
2024-2025学年人教版九年级上册数学期末试题重组练习
参考答案与试题解析
题号 1 2 3 4 5 6 7 8 9 10
答案 B D B C D B A A C D
一.选择题(共10小题)
1.(2023 恩施市校级期末)下列4个图形中,是中心对称图形的是( )
A. B. C. D.
【解答】解:选项A、C、D的图形都不能找到一个点,使这些图形绕某一点旋转180°与原来的图形重合,所以不是中心对称图形;
选项B的图形能找到一个点,使这个图形绕某一点旋转180°与原来的图形重合,所以是中心对称图形;
故选:B.
2.(2023 连州市期末)如果方程mx2﹣6x+1=0有实数根,那么m的取值范围是( )
A.m<9且m≠0 B.m≤9且m≠0 C.m<9 D.m≤9
【解答】解:∵关于x的方程mx2﹣6x+1=0有实数根,
∴当方程是一元二次方程时,Δ=(﹣6)2﹣4m≥0,
解得:m≤9,且m≠0;
当方程是一元一次方程时,则m=0,
故选:D.
3.(2023秋 柳北区期末)下列函数属于二次函数的是( )
A.y=2x B.y=2x2﹣1 C. D.y=x﹣2+1
【解答】解:A、y=2x是一次函数,不是二次函数;
B、y=2x2﹣1是二次函数;
C、不是二次函数;
D、y=x﹣2+1不是二次函数;
故选:B.
4.(2023 东海县模拟)下列语句中不正确的有( )
①相等的圆心角所对的弧相等;
②平分弦的直径垂直于弦;
③圆是轴对称图形,任何一条直径都是它的对称轴;
④半圆是弧.
A.1个 B.2个 C.3个 D.4个
【解答】解:①、要强调在同圆或等圆中相等的圆心角所对的弧相等;故错误.
②、平分弦的直径垂直于弦,其中被平分的弦不能是直径,若是直径则错误.
③、对称轴是直线,而直径是线段,故错误.
④、正确.
故选:C.
5.(2023秋 龙口市期末)将二次函数y=(x+1)2的图象向上平移2个单位,得到的图象对应的函数表达式是( )
A.y=(x+3)2 B.y=(x﹣1)2
C.y=(x+1)2﹣2 D.y=(x+1)2+2
【解答】解:由题可知,二次函数y=(x+1)2的图象向上平移了2个单位,根据规律可得出平移后的函数表达式为y=(x+1)2+2.
故选:D.
6.(2023秋 麻章区校级期末)下列说法正确的是( )
A.“清明时节雨纷纷”是必然事件
B.为了了解某小区居民新冠疫苗注射情况,可以采用全面调查方式进行
C.一组数据2,5,4,5,6,7的众数、中位数和平均数都是4.5
D.甲、乙两组队员身高数据的方差分别为,,那么甲组队员身高比较整齐
【解答】解:A.“清明时节雨纷纷”是随机事件,原说法错误,不符合题意;
B.为了了解某小区居民新冠疫苗注射情况,可以采用全面调查方式进行,正确,符合题意
C.一组数据2,5,4,5,6,7的众数是5,中位数是5,平均数是,原说法错误,不符合题意;
D.甲、乙两组队员身高数据的方差分别为,,那么乙队员身高比较整齐,原说法错误,不符合题意,
故选:B.
7.(2023秋 长子县期末)某大型连锁超市以17元/斤的价格购进草莓1万斤,在运输、储存过程中部分草莓损坏,超市管理员从所有的草莓中随机抽取了若干进行“草莓损坏率”统计,并把获得的数据记录如表:
草莓总质量n/斤 20 50 100 200 500
损坏草莓质量m/斤 3.12 7.7 15.2 29.8 75
草莓损坏的频率 0.156 0.154 0.152 0.149 0.150
超市管理员希望卖出草莓(损坏的草莓不能出售)可以获得利润42500元,那么就需要利用草莓损坏的概率(精确到0.01)估算草莓的售价.根据表中数据可以估计,草莓每斤的售价应该定为( )
A.25元 B.22元 C.21.25元 D.21.5元
【解答】解:由表格中的数据可得草莓的损坏率大约为15%,
则完好率为:1﹣15%=85%,
设每斤草莓的售价为x元,根据题意得,
10000×x×85%﹣10000×17=42500,
解得,x=25,
即每斤草莓的售价为25元,
故选:A.
8.(2023秋 广饶县期末)如图,AB是⊙O的直径,∠ACD=15°,则∠BAD的度数为( )
A.75° B.65° C.60° D.85°
【解答】解:连接BD,
∵AB是⊙O的直径,
∴∠ADB=90°,
又∵∠C=∠B=15°,
∴∠BAD=90°﹣∠B=90°﹣15°=75°,
故选:A.
9.(2023秋 鼓楼区校级期末)近年来,我国数字技术不断革新,影响着全民阅读形态.为预计某市2023年数字阅读市场规模,经查询得数据:该市2021年数字阅读市场规模为432万元,2023年数字阅读市场规模为507万元.设该市年平均增长率为x,则下列方程正确的是( )
A.432(1+2x)=507
B.432(1+2x)2=507
C.432(1+x)2=507
D.432+432(1+x)+432(1+x)2=507
【解答】解:根据题意得:432(1+x)2=507.
故选:C.
10.(2023秋 陇西县期末)二次函数y=ax2+bx+c(a≠0)的图象如图所示,当y<0时自变量x的取值范围是( )
A.x<﹣3 B.x>1 C.x<﹣3或x>1 D.﹣3<x<1
【解答】解:由图可知,﹣3<x<1时,y<0.
故选:D.
二.填空题(共8小题)
11.(2023秋 琼中县期末)一元二次方程x2﹣2x+8=0的常数项是 8 .
【解答】解:一元二次方程x2﹣2x+8=0的常数项是8.
故答案为:8.
12.(2023秋 连州市期末)如图是两个各自分割均匀的转盘,同时转动两个转盘,转盘停止时(若指针恰好停在分割线上,则重转一次,直到指针指向某一个区域为止),两个指针所指区域的数字之和为奇数的概率是 .
【解答】解:列表如下:
1 2 3 4
2 (2,1) (2,2) (2,3) (2,4)
3 (3,1) (3,2) (3,3) (3,4)
4 (4,1) (4,2) (4,3) (4,4)
共有12种等可能的结果,其中两个指针所指区域的数字之和为奇数的结果有:(2,1),(2,3),(3,2),(3,4),(4,1),(4,3),共6种,
∴两个指针所指区域的数字之和为奇数的概率为.
故答案为:.
13.(2023秋 平邑县期末)在平面直角坐标系中,点A(5,m+1)与点B(﹣5,﹣3)关于原点对称,则m的值为 2 .
【解答】解:∵点A(5,m+1)与点B(﹣5,﹣3)关于原点对称,
∴m+1=3,
解得:m=2.
故答案为:2.
14.(2023秋 平邑县期末)抛物线y=﹣0.5x2+bx+3的部分图象如图所示,则一元二次方程﹣0.5x2+bx+3=0的根为 x1=1,x2=﹣3 .
【解答】解:由图象得:抛物线y=﹣0.5x2+bx+3与x轴的一个交点为(1,0),且对称轴为直线x=﹣1,
∴抛物线y=﹣0.5x2+bx+3与x轴的另一个交点为(﹣3,0),
故一元二次方程﹣0.5x2+bx+3=0的根为:x1=1,x2=﹣3,
故答案为:x1=1,x2=﹣3.
15.(2023秋 准格尔旗期末)如图,点M是边长为2的正六边形ABCDEF内的一点(不包括边界),且AM⊥BM,P是FC上的一点,N是AF的中点,则PN+PM的最小值为 2 .
【解答】解:取AB中点O,EF中点Q,连接PQ,MO,延长EF、BA相交于点T,
,
∵正六边形ABCDEF关于直线CF对称,
∴N,Q也关于直线CF对称,
∴PQ=PN,
∵AM⊥BM,O为AB中点,
∴,
∴PN+PM+MO=PQ+PM+MO≥QO,
当Q,P,M,O共线时,PN+PM+MO=PQ+PM+MO=QO,
∴PN+PM的最小值为QO﹣MO=QM,
∵正六边形ABCDEF的边长为2,
∴,AF=EF=AB=2,
∴△TAF是等边三角形,
∴FT=AT,∠T=60°,
∵EF=AB=2,O为AB中点,Q为EF中点,
∴,,
∴TQ=3=TO,
∴△TQO是等边三角形,
∴QO=3,
∴QM=2,
∴PN+PM的最小值为2.
故答案为:2.
16.(2023秋 龙口市期末)二次函数的图象如图所示,点O为坐标原点,点A在y轴的正半轴上,点B、C在函数图象上,四边形OBAC为菱形,且∠BOC=60°,则菱形OBAC的面积为 .
【解答】解:连接BC交OA于D,如图,
∵四边形OBAC为菱形,
∴BC⊥OA,
∵∠BOC=60°,
∴∠BOD=30°,
∴,
设BD=t,则,
∴,
把代入,
得,
解得t1=0(舍去),t2=1,
∴BD=1,,
∴BC=2,,
∴菱形OBAC的面积为:,
故答案为:.
17.(2023秋 湖北期末)筒车是我国古代发明的一种水利灌溉工具,明朝科学家徐光启在《农政全书》中用图画描绘了筒车的工作原理,如图1,筒车盛水桶的运行轨道是以轴心O为圆心的圆,如图2,已知圆心O在水面上方,且⊙O被水面截得的弦AB长为8米,⊙O的半径长为5米.若点C为运行轨道的最低点,则点C到弦AB所在直线的距离是 2 米.
【解答】解:如下图所示,连接OA、OC,
∵OC交AB于点E,则有OE⊥AB,
∴(米),
又∵OA=OC=5米,
在Rt△AOE中,(米),
∴CE=CO﹣OE=5﹣3=2(米),
答:若点C为运行轨道的最低点,则点C到弦AB所在直线的距离是2米.
故答案为:2.
18.(2023秋 柳北区期末)如图,四边形ABCD内接于⊙O,点E在CD的延长线上.若∠ADE=70°,则∠AOC= 140 度.
【解答】解:∵∠ADE=70°,
∴∠ADC=180°﹣∠ADE=180°﹣70°=110°,
∵四边形ABCD内接于⊙O,
∴∠ABC+∠ADC=180°,
∴∠ABC=180°﹣110°=70°,
由圆周角定理得:∠AOC=2∠ABC=140°,
故答案为:140.
三.解答题(共8小题)
19.(2023秋 息县校级期末)解方程:
(1)x2﹣2x﹣8=0;
(2)(x+4)2=5(x+4).
【解答】解:(1)x2﹣2x﹣8=0.
(x﹣4)(x+2)=0,
(x﹣4)=0,(x+2)=0,
∴x1=4,x2=﹣2;
(2)(x+4)2﹣5(x+4)=0,
(x+4)(x+4﹣5)=0,
∴x+4=0或x﹣1=0,
∴x1=﹣4,x2=1.
20.(2023秋 乳山市期末)某种品牌的护眼罩分为三种型号,分别用A,B,C表示,假设它们被购买者选中的可能性均相同.小明和小强分别购买了一种型号的护眼罩,用列表法或画树状图法,求出小明和小强选择同一种型号护眼罩的概率.
【解答】解:树状图如下所示,
由上可得,共有9种等可能结果,小明和小强选择同一种型号护眼罩有3种结果.
∴P(同一种型号)=,
即小明和小强选择同一种型号护眼罩的概率是.
21.(2023秋 亳州期末)某商店购进一批单价为20元的日用商品,如果以单价30元销售,那么一个月内可以售出400件.根据销售经验,提高销售单价会导致销售量的减少,即销售单价每提高1元,销售量相应减少20件.售价为多少元时,才能在一个月内获得最大利润?
【解答】解:设销售单价为x元,销售利润为y元.
根据题意,得:
y=(x﹣20)[400﹣20(x﹣30)]
=(x﹣20)(1000﹣20x)
=﹣20x2+1400x﹣20000
=﹣20(x﹣35)2+4500,
∵﹣20<0,
∴x=35时,y有最大值.
所以,销售单价为35元,才能在一个月内获得最大利润.
22.(2023秋 高青县期末)如图,在边长均为1个单位长度的小正方形组成的网格中,点A,B,O均为格点(每个小正方形的顶点叫做格点).
(1)作点A关于点O的对称点A1;
(2)连接A1B,将线段A1B绕点A1顺时针旋转90°得到线段A1B1,点B的对应点为B1,画出旋转后的线段A1B1;
(3)连接AB1,BB1,求出△ABB1的面积(直接写出结果即可).
【解答】解:(1)如图所示,点A1即为所求;
(2)如图所示,线段A1B1即为所求;
(3)如图,连接AB1,BB1,
则=×8×2=8.
23.(2023秋 城中区校级月考)如图,抛物线y=x2﹣9与x轴交于A、B两点,
(1)求A、B两点的坐标;
(2)点P为抛物线上一点,且S△PAB=6,求P点的坐标.
【解答】解:(1)抛物线y=x2﹣9,令y=0,得到x=3或﹣3,即A(﹣3,0),B(3,0);
(2)由点A、B的坐标可知:AB=6,
∵S△PAB=6,设P纵坐标为b,
∴×6|b|=6,即|b|=2,
∴b=2或﹣2,
当b=2时,x2﹣9=2,解得:x=±,此时P坐标为(,2),(﹣,2);
当b=﹣2时,x2﹣9=﹣2,解得:x=±,此时P坐标为(,﹣2),(﹣,﹣2),
综上,P的坐标为(,2)或(﹣,2)或(,﹣2)或(﹣,﹣2).
24.(2023秋 城中区校级月考)阅读材料回答问题:
为解方程(x2﹣1)2﹣5(x2﹣1)+4=0,我们可将x2﹣1视为一个整体,然后设x2﹣1=y,则(x2﹣1)2=y2,原方程可化为y2﹣5y+4=0①.
解得y1=1,y2=4,当y=1时,x2﹣1=1,所以x2=2,x=±;
当y=4时,x2﹣1=4,所以x2=5,x=±;
所以原方程的解为,x2=﹣,x1=,x2=﹣y.
解方程:(x2+1)2+4(x2+1)﹣12=0.
【解答】解:(x2+1)2+4(x2+1)﹣12=0,
设y=x2+1,
则原方程化为y2+4y﹣12=0,
(y+6)(y﹣2)=0,
∴y1=﹣6,y2=2,
∵y=x2+1>1,
∴y1=﹣6(舍去),
∴x2+1=2,
x2=1,
x1=1,x2=﹣1.
25.(2023秋 天津月考)如图,抛物线y=ax2+bx+3(a<0)与x轴交于A(﹣1,0),B两点,与y轴交于点C,对称轴为直线x=1.
(1)直接写出抛物线的解析式;
(2)P是抛物线上一动点(不与点C重合),直线CP交对称轴于点AN,连接AN,当∠ANC=45°时,求直线PC的解析式.
【解答】解:(1)根据题意得,即b=﹣2a,
∴y=ax2﹣2ax+3,
∵A(﹣1,0),
∴a+2a+3=0,
解得a=﹣1,
∴抛物线解析式为y=﹣x2+2x+3;
(2)如图所示,过点A作AM⊥AN交直线CP于M,过点M作MQ⊥x轴于Q,
设抛物线对称轴与x轴交点为D,
∴∠AQM=∠MAN=∠NDA=90°,D(1,0),
∴∠AMQ+∠MAQ=90°,
又∵∠MAQ+∠NAD=90°,
∴∠AMQ=∠NAD,
∴∠AMN=∠ANM=45°,
∴AM=NA,
∴△AMQ≌△NAD(AAS),
∴MQ=AD,AQ=ND,
设直线CP的解析式为y=kx+3,点N的坐标为(1,k+3),
∵当k+3>0时,A(﹣1,0),D(1,0),
∴MQ=AD=2,AQ=ND=k+3,
∴OQ=k+4,
∴点M的坐标为(﹣k﹣4,2),
∴k(﹣k﹣4)+3=2,即k2+4k﹣1=0,
解得或(舍去),
∴直线PC的解析式为,
同理可得当k+3≤0时,
解得y=﹣x+3.
综上所述,或y=﹣x+3.
26.(2023秋 鼓楼区校级期末)如图,△ABC中,AB=AC,点O是底边BC的中点,腰AB与⊙O相切于点D.
(1)求证:AC是⊙O的切线;
(2)若⊙O的半径为2,∠C=45°,求图中阴影部分的面积.
【解答】(1)证明:过点O作OG⊥AC于点G,连接AO,OD,
∵AB是⊙O的切线,
∴OD⊥AB,
∵点O是底边BC的中点,
∴OB=OC,
∵AB=AC,
∴AO平分∠BAC,AO⊥BC,
∴OD=OG,
∵OG是圆的半径,
∴AC是⊙O的切线;
(2)解:∵AB=AC,∠C=45°,
∴∠B=∠C=45°,
∴∠BAC=90°,即△BAC为等腰直角三角形,
∵∠ADO=∠AGO=90°,
∴四边形ADOG是矩形,
∵OD=OG,
∴四边形ADOG是正方形,
∴AD=OD=OG=AG=2,∠DOG=90°,
∴阴影部分的面积为.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
