2024-2025学年北师大版数学八年级上学期期末综合练习(含答案)
文档属性
| 名称 | 2024-2025学年北师大版数学八年级上学期期末综合练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 369.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-12 14:29:40 | ||
图片预览


文档简介
2024-2025学年北师大版数学八年级上学期期末综合练习
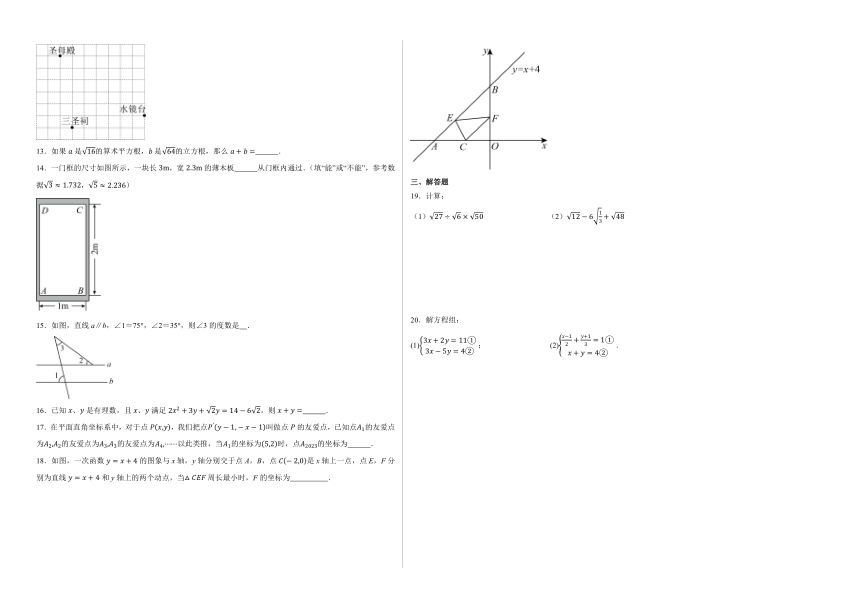
学校:___________姓名:___________班级:___________
一、单选题
1.根据下列表述,能确定位置的是( )
A.光明剧院2排 B.某市人民路 C.北偏东 D.东经,北纬
2.某运动员进行赛前训练,如果对他30次训练成绩进行统计分析,判断他的成绩是否稳定,则需要知道这10次成绩的( ).
A.众数 B.方差 C.平均数 D.中位数
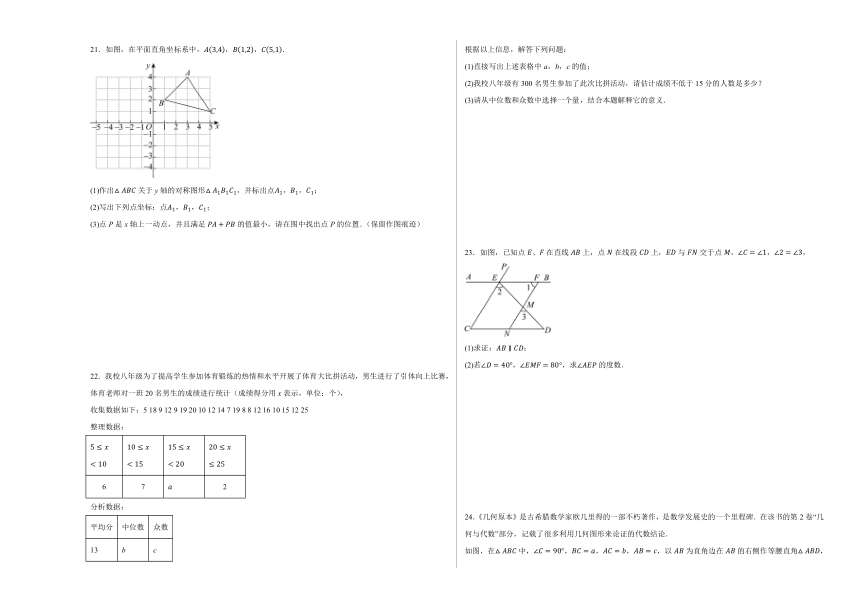
3.在直角三角形中,有两边分别为6和8,则第三边是( )
A.8 B.10 C. D.10或
4.下面哪个点在函数y=2x+4的图象上( )
A.(2,1) B.(-2,1) C.(2,0) D.(-2,0)
5.在同一平面直角坐标系中,函数与的图象大致是( )
A.B. C. D.
6.利用计算器计算出的下表各数的算术平方根如下,则a的值是( )
……
25 a ……
A. B. C. D.
7.如图,已知△ABC中,BD、CE分别是∠ABC、∠ACB的角平分线,BD与CE交于点O.如果∠BAC=n°,那么用含n的代数式表示∠BOC( )
A.(45+n)° B.(180﹣n)° C.(90+n)° D.(90+n)°
8.已知和是二元一次方程的两组解,则一次函数的图像与y轴的交点坐标是( )
A. B. C. D.
9.如图,某超市为了吸引顾客,在超市门口离地高4.5m的墙上,装有一个由传感器控制的门铃A,如①图所示,人只要移至该门口4m及4m以内时,门铃就会自动发出语音“欢迎光临”.如②图所示,一个身高1.5m的学生走到D处,门铃恰好自动响起,则该生头顶C到门铃A的距离为( )
A.3米 B.4米 C.5米 D.6米
10.甲、乙两人沿相同的路线由A到B匀速行进,A、B两地间的路程为16km,他们行进的路程S(km)与甲出发后的时间t(h)之间的函数图象如图所示,则下列判断错误的是()
A.乙比甲晚出发1h B.甲比乙晚到B地2 h
C.乙的速度是8km/h D.甲的速度是4km/h
二、填空题
11.在学校数学课外活动竞赛中,某班5名学生参赛成绩分别为:81,83,85,88,88,则这5名学生的参赛成绩的平均数为 ,方差 .
12.“去山西看古建!”首个国产游戏《黑神话:悟空》引发了前往山西旅游的热潮,其中太原晋祠景区备受人们欢迎.如图所示是太原晋祠景区部分景点,若圣母殿的坐标为,水镜台的坐标为,则三圣祠的坐标为 .
13.如果是的算术平方根,是的立方根,那么 .
14.一门框的尺寸如图所示,一块长,宽的薄木板 从门框内通过.(填“能”或“不能”,参考数据,)
15.如图,直线a∥b,∠1=75°,∠2=35°,则∠3的度数是 .
16.已知、是有理数,且、满足,则 .
17.在平面直角坐标系中,对于点,我们把点叫做点的友爱点,已知点的友爱点为的友爱点为的友爱点为以此类推,当的坐标为时,点的坐标为 .
18.如图,一次函数的图象与x轴,y轴分别交于点A,B,点是x轴上一点,点E,F分别为直线和y轴上的两个动点,当周长最小时,F的坐标为 .
三、解答题
19.计算:
(1) (2)
20.解方程组:
(1); (2).
21.如图,在平面直角坐标系中,,,.
(1)作出关于y轴的对称图形,并标出点,,;
(2)写出下列点坐标:点,,;
(3)点P是x轴上一动点,并且满足的值最小,请在图中找出点P的位置.(保留作图痕迹)
22.我校八年级为了提高学生参加体育锻炼的热情和水平开展了体育大比拼活动,男生进行了引体向上比赛,体育老师对一班20名男生的成绩进行统计(成绩得分用x表示,单位:个),
收集数据如下:5 18 9 12 9 19 20 10 12 14 7 19 8 8 12 16 10 15 12 25
整理数据:
6 7 2
分析数据:
平均分 中位数 众数
13 b c
根据以上信息,解答下列问题:
(1)直接写出上述表格中a,b,c的值;
(2)我校八年级有300名男生参加了此次比拼活动,请估计成绩不低于15分的人数是多少?
(3)请从中位数和众数中选择一个量,结合本题解释它的意义.
23.如图,已知点、在直线上,点在线段上,与交于点,,,
(1)求证:;
(2)若,,求的度数.
24.《几何原本》是古希腊数学家欧几里得的一部不朽著作,是数学发展史的一个里程碑.在该书的第2卷“几何与代数”部分,记载了很多利用几何图形来论证的代数结论.
如图,在中,,,,,以为直角边在的右侧作等腰直角,其中,,过点作,垂足为点.
(1)求证:,;
(2)请你用两种不同的方法表示梯形的面积,并证明:;
(3)若,,求中边上的高.
25.小明在学习二次根式后,发现一些含根号的式子可以写成另一个式子的平方,如:,善于思考的小明利用完全平方公式进行了以下探索:
.请你仿照小明的方法解决下列问题:
(1),则______,_______;
(2)已知是的算术平方根,求的值;
(3)当时,化简_______.
26.一批货物要运往某地,货主准备租用汽车运输公司的甲、乙两种货车,已知过去两次租用这两种货车的情况如下表:
第一次 第二次
甲种货车的辆数
乙种货车的辆数
累计运货的吨数
(1)现租用该公司辆甲种货车及辆乙种货车一次刚好运完这批货物,如果按每吨付运费元计算,货主应付运费多少元?
(2)能否租用这两种货车一次恰好运走吨货物(不超载也不少运)?若能,请说出有哪几种装运方案?若不能,请说明理由.
27.无人快递车在部分城市道路上正式“上岗”.现有一条笔直的路上依次有,,三个快递网点,其中,两网点相距米.甲、乙两车分别从,两网点同时出发,匀速行驶去往目的地,.图中,分别表示甲、乙两车离地的距离(米)与行驶时间(分钟)的函数关系图象.
(1)直线的函数表达式为_____;
(2)出发后甲快递车行驶多长时间,与乙快递车相遇?
(3)甲快递车到网点后,再经过分钟乙车也到网点,求,两网点间的距离.
参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 D B D D C A D C C C
11. 85
12.
13.4
14.不能
15.40°.
16.或
17.
18.
19.解:(1)原式=
=
=
=15;
(2)原式=
=.
20.(1)解:,
,得,
解得,
把代入①,得,
解得,
所以方程组的解为;
(2)解:,
整理①得,即,
所以整理②得,
把代入,
得,
解得,
把代入,
解得,
所以方程组的解为.
21.(1)解:如图所示,为所作;
;
(2)解:如图,,,;
(3)解:如图,连接交x轴于P.P点即为所求.
22.(1)将这组数据重新排列为:5、7、8、8、9、9、10、10、12、12、12、12、14、15、16、18、19、19、20、25,
的人数,中位数,众数;
(2)(人,
答:估计成绩不低于15分的人数是105人;
(3)中位数,
抽取的20名学生成绩中,中位数是12分,有一半学生的成绩都不低于12分(答案不唯一).
23.1)证明:∵,
∴,
∴,
又∵,
∴,
∴;
(2)解:∵,
∴,
又∵,
∴,
∴.
24.(1)证明:∵,
∴,
∵,
∴,
∵,
∴,
∵中,,
∴,
∴.
在和中,
∴,
∴,.
(2)证明:,
,
∴,
∴,
∴,
∴;
(3)解:∵,,,
∴,
∵为边长,为正值,
∴,
∵,
∴.
∴.
25.解:(1)∵,
∴a=2,b=1;
(2)∵是的算术平方根,
∴,
∴;
(3)∵,
∴,
,
,
,
.
26.(1)解:设甲种货车每辆运货吨,乙种货车每辆运货吨,
根据表格可得:,
解得,
甲种货车每辆运货吨,乙种货车每辆运货吨,
现租用该公司辆甲种货车及辆乙种货车一次刚好运完这批货物,
这批货物有吨,
元,
货主应付运费元;
(2)能租用这两种货车一次恰好运走吨货物,理由如下:
设租用甲种货车辆,乙种货车辆恰好运走吨货物,
,
,
当时,;
当时,;
当时,;
一共有种装运方案:租用甲种货车辆,乙种货车辆或租用甲种货车辆,乙种货车辆或租用甲种货车辆,乙种货车辆.
27.(1)解:设直线的函数表达式为,
将代入得:,
解得:,
∴直线的函数表达式为.
(2)解:设直线的函数表达式为,
将,代入得:,
解得:,
∴直线的函数表达式为.
联立两直线函数表达式组成方程组:,
解得:,,
∴出发后甲快递车行驶分钟,与乙快递车相遇;
(3)解:根据题意得:,
解得:,
∴,
∴,两网点间的距离为(米).
学校:___________姓名:___________班级:___________
一、单选题
1.根据下列表述,能确定位置的是( )
A.光明剧院2排 B.某市人民路 C.北偏东 D.东经,北纬
2.某运动员进行赛前训练,如果对他30次训练成绩进行统计分析,判断他的成绩是否稳定,则需要知道这10次成绩的( ).
A.众数 B.方差 C.平均数 D.中位数
3.在直角三角形中,有两边分别为6和8,则第三边是( )
A.8 B.10 C. D.10或
4.下面哪个点在函数y=2x+4的图象上( )
A.(2,1) B.(-2,1) C.(2,0) D.(-2,0)
5.在同一平面直角坐标系中,函数与的图象大致是( )
A.B. C. D.
6.利用计算器计算出的下表各数的算术平方根如下,则a的值是( )
……
25 a ……
A. B. C. D.
7.如图,已知△ABC中,BD、CE分别是∠ABC、∠ACB的角平分线,BD与CE交于点O.如果∠BAC=n°,那么用含n的代数式表示∠BOC( )
A.(45+n)° B.(180﹣n)° C.(90+n)° D.(90+n)°
8.已知和是二元一次方程的两组解,则一次函数的图像与y轴的交点坐标是( )
A. B. C. D.
9.如图,某超市为了吸引顾客,在超市门口离地高4.5m的墙上,装有一个由传感器控制的门铃A,如①图所示,人只要移至该门口4m及4m以内时,门铃就会自动发出语音“欢迎光临”.如②图所示,一个身高1.5m的学生走到D处,门铃恰好自动响起,则该生头顶C到门铃A的距离为( )
A.3米 B.4米 C.5米 D.6米
10.甲、乙两人沿相同的路线由A到B匀速行进,A、B两地间的路程为16km,他们行进的路程S(km)与甲出发后的时间t(h)之间的函数图象如图所示,则下列判断错误的是()
A.乙比甲晚出发1h B.甲比乙晚到B地2 h
C.乙的速度是8km/h D.甲的速度是4km/h
二、填空题
11.在学校数学课外活动竞赛中,某班5名学生参赛成绩分别为:81,83,85,88,88,则这5名学生的参赛成绩的平均数为 ,方差 .
12.“去山西看古建!”首个国产游戏《黑神话:悟空》引发了前往山西旅游的热潮,其中太原晋祠景区备受人们欢迎.如图所示是太原晋祠景区部分景点,若圣母殿的坐标为,水镜台的坐标为,则三圣祠的坐标为 .
13.如果是的算术平方根,是的立方根,那么 .
14.一门框的尺寸如图所示,一块长,宽的薄木板 从门框内通过.(填“能”或“不能”,参考数据,)
15.如图,直线a∥b,∠1=75°,∠2=35°,则∠3的度数是 .
16.已知、是有理数,且、满足,则 .
17.在平面直角坐标系中,对于点,我们把点叫做点的友爱点,已知点的友爱点为的友爱点为的友爱点为以此类推,当的坐标为时,点的坐标为 .
18.如图,一次函数的图象与x轴,y轴分别交于点A,B,点是x轴上一点,点E,F分别为直线和y轴上的两个动点,当周长最小时,F的坐标为 .
三、解答题
19.计算:
(1) (2)
20.解方程组:
(1); (2).
21.如图,在平面直角坐标系中,,,.
(1)作出关于y轴的对称图形,并标出点,,;
(2)写出下列点坐标:点,,;
(3)点P是x轴上一动点,并且满足的值最小,请在图中找出点P的位置.(保留作图痕迹)
22.我校八年级为了提高学生参加体育锻炼的热情和水平开展了体育大比拼活动,男生进行了引体向上比赛,体育老师对一班20名男生的成绩进行统计(成绩得分用x表示,单位:个),
收集数据如下:5 18 9 12 9 19 20 10 12 14 7 19 8 8 12 16 10 15 12 25
整理数据:
6 7 2
分析数据:
平均分 中位数 众数
13 b c
根据以上信息,解答下列问题:
(1)直接写出上述表格中a,b,c的值;
(2)我校八年级有300名男生参加了此次比拼活动,请估计成绩不低于15分的人数是多少?
(3)请从中位数和众数中选择一个量,结合本题解释它的意义.
23.如图,已知点、在直线上,点在线段上,与交于点,,,
(1)求证:;
(2)若,,求的度数.
24.《几何原本》是古希腊数学家欧几里得的一部不朽著作,是数学发展史的一个里程碑.在该书的第2卷“几何与代数”部分,记载了很多利用几何图形来论证的代数结论.
如图,在中,,,,,以为直角边在的右侧作等腰直角,其中,,过点作,垂足为点.
(1)求证:,;
(2)请你用两种不同的方法表示梯形的面积,并证明:;
(3)若,,求中边上的高.
25.小明在学习二次根式后,发现一些含根号的式子可以写成另一个式子的平方,如:,善于思考的小明利用完全平方公式进行了以下探索:
.请你仿照小明的方法解决下列问题:
(1),则______,_______;
(2)已知是的算术平方根,求的值;
(3)当时,化简_______.
26.一批货物要运往某地,货主准备租用汽车运输公司的甲、乙两种货车,已知过去两次租用这两种货车的情况如下表:
第一次 第二次
甲种货车的辆数
乙种货车的辆数
累计运货的吨数
(1)现租用该公司辆甲种货车及辆乙种货车一次刚好运完这批货物,如果按每吨付运费元计算,货主应付运费多少元?
(2)能否租用这两种货车一次恰好运走吨货物(不超载也不少运)?若能,请说出有哪几种装运方案?若不能,请说明理由.
27.无人快递车在部分城市道路上正式“上岗”.现有一条笔直的路上依次有,,三个快递网点,其中,两网点相距米.甲、乙两车分别从,两网点同时出发,匀速行驶去往目的地,.图中,分别表示甲、乙两车离地的距离(米)与行驶时间(分钟)的函数关系图象.
(1)直线的函数表达式为_____;
(2)出发后甲快递车行驶多长时间,与乙快递车相遇?
(3)甲快递车到网点后,再经过分钟乙车也到网点,求,两网点间的距离.
参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 D B D D C A D C C C
11. 85
12.
13.4
14.不能
15.40°.
16.或
17.
18.
19.解:(1)原式=
=
=
=15;
(2)原式=
=.
20.(1)解:,
,得,
解得,
把代入①,得,
解得,
所以方程组的解为;
(2)解:,
整理①得,即,
所以整理②得,
把代入,
得,
解得,
把代入,
解得,
所以方程组的解为.
21.(1)解:如图所示,为所作;
;
(2)解:如图,,,;
(3)解:如图,连接交x轴于P.P点即为所求.
22.(1)将这组数据重新排列为:5、7、8、8、9、9、10、10、12、12、12、12、14、15、16、18、19、19、20、25,
的人数,中位数,众数;
(2)(人,
答:估计成绩不低于15分的人数是105人;
(3)中位数,
抽取的20名学生成绩中,中位数是12分,有一半学生的成绩都不低于12分(答案不唯一).
23.1)证明:∵,
∴,
∴,
又∵,
∴,
∴;
(2)解:∵,
∴,
又∵,
∴,
∴.
24.(1)证明:∵,
∴,
∵,
∴,
∵,
∴,
∵中,,
∴,
∴.
在和中,
∴,
∴,.
(2)证明:,
,
∴,
∴,
∴,
∴;
(3)解:∵,,,
∴,
∵为边长,为正值,
∴,
∵,
∴.
∴.
25.解:(1)∵,
∴a=2,b=1;
(2)∵是的算术平方根,
∴,
∴;
(3)∵,
∴,
,
,
,
.
26.(1)解:设甲种货车每辆运货吨,乙种货车每辆运货吨,
根据表格可得:,
解得,
甲种货车每辆运货吨,乙种货车每辆运货吨,
现租用该公司辆甲种货车及辆乙种货车一次刚好运完这批货物,
这批货物有吨,
元,
货主应付运费元;
(2)能租用这两种货车一次恰好运走吨货物,理由如下:
设租用甲种货车辆,乙种货车辆恰好运走吨货物,
,
,
当时,;
当时,;
当时,;
一共有种装运方案:租用甲种货车辆,乙种货车辆或租用甲种货车辆,乙种货车辆或租用甲种货车辆,乙种货车辆.
27.(1)解:设直线的函数表达式为,
将代入得:,
解得:,
∴直线的函数表达式为.
(2)解:设直线的函数表达式为,
将,代入得:,
解得:,
∴直线的函数表达式为.
联立两直线函数表达式组成方程组:,
解得:,,
∴出发后甲快递车行驶分钟,与乙快递车相遇;
(3)解:根据题意得:,
解得:,
∴,
∴,两网点间的距离为(米).
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
