上海市金山区2024-2025学年九年级上学期期末数学试卷(一模)(图片版,无答案)
文档属性
| 名称 | 上海市金山区2024-2025学年九年级上学期期末数学试卷(一模)(图片版,无答案) |

|
|
| 格式 | |||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-01-11 23:20:02 | ||
图片预览

文档简介
金山2024学年第一学期期末学情诊断
初三数学试卷
(考试时间100分钟,满分150分)
2025.1
考生注意:
1,本试卷含三个大愿,共25愿:答题时,考生务必按答思要求在答题纸规定的位置上作
容,在草稿纸、本试卷上答愿一律无效:
2.除第一、二大愿外,其余各题如无特别说明,都必须在答题纸的相应位置上写出证明成
计算的主要步康.
一、选择题(本大题共6题,每题4分,满分24分)
【下列各思的四个选项中,有且只有一个选项是正确的,选择正确的选项并填涂在答思纸
的相应位显上.】
1.下列函数中,一定是二次函数的是(▲)
(A)y=三x+m(其中m是常数
(B)y=+br+c(其中a、b、c是常致):
(C)y=(2x-I)x:
(D)y=(x+4)2-x2.
2.已知R△ABC中,∠C=90°,AC=3,AB=5,那么下列各式中,正确的是(▲)
A)如B=:
(B)c0sB=3
(C)cotB=3
5
(D)tanB
3.在平面直角坐标系x0y中,对于抛物线y=-(x-20)+25,下列叙述正确的是(▲)
(A)抛物线有最低点,最低点的坐标是(20,25):
(B)抛物线有最高点,最高点的坐标是(-20,25):
(C)抛物线有最高点,最高点的坐标是(20,25):
(D)抛物线有最低点,最低点的坐标是(-20,25).
4.下列说法中,正确的是(▲)
(A)两个停腰三角形一定相似:
(B)两个直角三角形一定相似:
(C)含45°角的两个等腰三角形一定相似:
(D)含105°角的两个等腰三角形一定相似,
5.在△ABC中,点D,E分别是边AB,AC的中点,下列结论中,错误的是(▲)
(A)△ADE∽△ABC:
《B)S。Aoe三25c
(C)DE=÷BC:
(D)DE∥BC.
6.己知二次函数y=∫(x)的图像是开口向上的抛物线,抛物线的对称轴在y轴右侧.当
抛物线与x轴两交点的距离为9时,若∫(-5)、∫(-)、∫(4)、∫(7)这四个函数值中有且
只有一个值不大于0,那么在这四个函数值中,值不大于0是(▲)
(A)f(-5):
(B)(-):
(c)f(4):
(D)f(7)·.
二、填空题(本大题共12题,每题4分,满分48分)
7.已知a、b是不等于0的实数,7a=5b,那么a+b
b
8.已如f(x)=4x-1.R么(2=▲_
9.将二次函&y=x2-4x+3化成y=a(+m)+k的形式为▲_
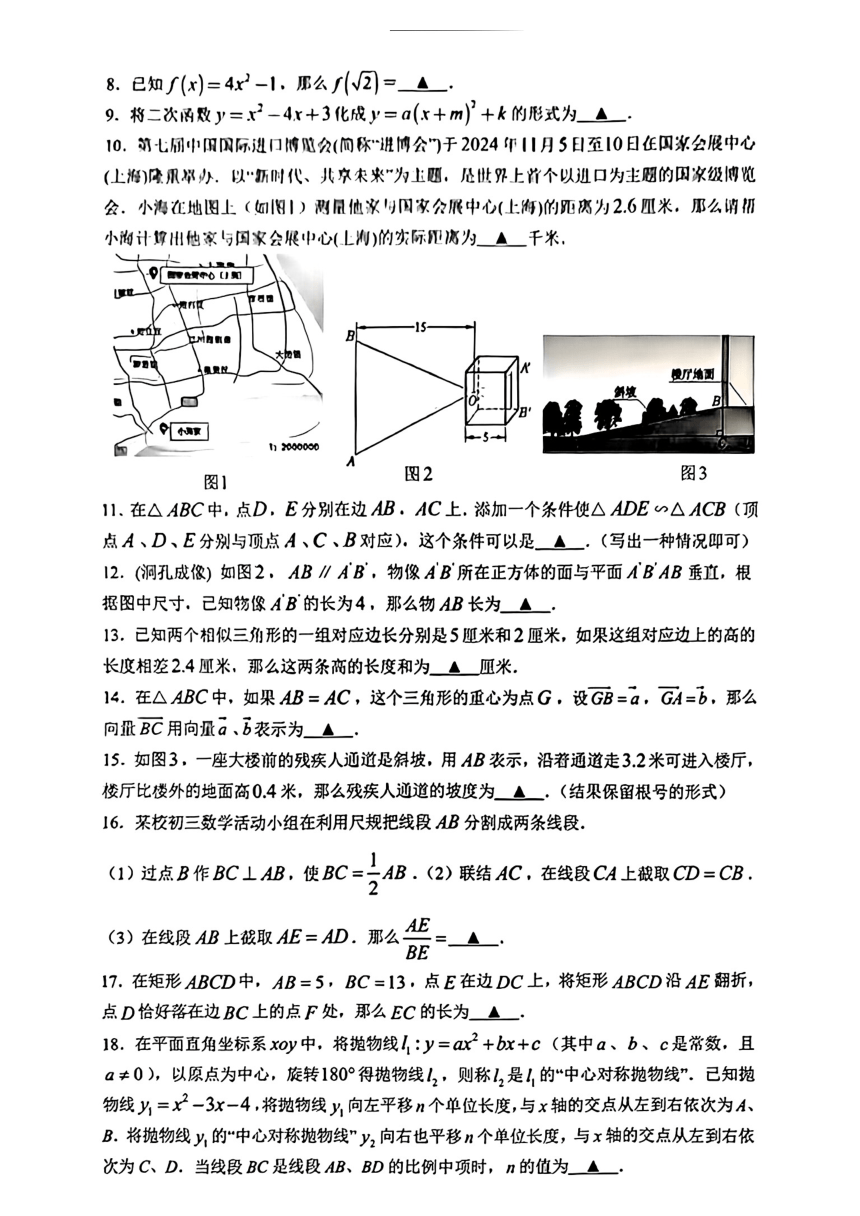
10.对七M中阳风际进门博建久(向你进博公)于2024年11月5日至10日E四家么展中心
(上将)风承深办.以历时代、共京宋来“为上题,是世界上首个以沮口为主题的四凉级博跑
会.小海在地图上(图1)测恨他汉回家会展中心(上海)的死离为2.6四米。那么峭历
小海计尊出他家与回家会展中心(上抑)的实际见滴为▲千米,
计自自
量
I12000030
图1
图2
图3
I1.在△ABC中,点D,E分别在边AB.AC上,添加一个条件使△ADE∽△ACB(项
点A、D、E分别与顶点A、C、B对应),这个条件可以是▲·(写出一种情况即可)
I2.(涧孔成侬)如图2,AB∥AB,物像AB所在正方体的面与平面ABAB垂直,根
据图中尺寸,己知物像AB的长为4,那么物AB长为▲·
13.已知两个相似三角形的一组对应边长分别是5埏米和2厘米,如果这组对应边上的高的
长度相差2.4厘米,那么这两条高的长度和为▲皿米,
14.在△ABC中,如果AB=AC,这个三角形的重心为点G,设G=a,GA=b,那么
向耻BC用向a、五丧示为▲一
15.如图3,一座大极前的残疾人酒道是斜坡。用AB丧示,沿着通道走32米可进入楼厅,
楼厅比楼外的地面高0.4米,那么残疾人通道的坡度为▲·(结果保留根号的形式)
16.来校初三致学活动小组在利用尺规把线段AB分割成两条线段.
(I)过点B作BC1AB,使BC=AB.(2)联结AC,在线段CA上藏取CD=CB.
(3)在线段AB上被取AE=AD.那么AE
=▲
BE
I7,在矩形ABCD中,AB=5,BC=I3,点E在边DC上,将矩形ABCD沿AE翻折,
点D怡好弦在边BC上的点F处,那么EC的长为▲、
18.在平面直角坐标系x0y中,将抛物线(:y=ax2+bx+c(其中a、b、c是常数,且
a≠0),以原点为中心,旋转180°得抛物线12,则称12是1的“中心对称抛物线”.己知抛
物线=x-3x-4,将抛物线y向左平移n个单位长度,与x轴的交点从左到右依次为A、
B.将抛物线y的中心对称抛物线”,向右也平移n个单位长度,与x轴的交点从左到右依
次为C、D.当线段BC是线段AB、BD的比例中项时,n的值为▲
初三数学试卷
(考试时间100分钟,满分150分)
2025.1
考生注意:
1,本试卷含三个大愿,共25愿:答题时,考生务必按答思要求在答题纸规定的位置上作
容,在草稿纸、本试卷上答愿一律无效:
2.除第一、二大愿外,其余各题如无特别说明,都必须在答题纸的相应位置上写出证明成
计算的主要步康.
一、选择题(本大题共6题,每题4分,满分24分)
【下列各思的四个选项中,有且只有一个选项是正确的,选择正确的选项并填涂在答思纸
的相应位显上.】
1.下列函数中,一定是二次函数的是(▲)
(A)y=三x+m(其中m是常数
(B)y=+br+c(其中a、b、c是常致):
(C)y=(2x-I)x:
(D)y=(x+4)2-x2.
2.已知R△ABC中,∠C=90°,AC=3,AB=5,那么下列各式中,正确的是(▲)
A)如B=:
(B)c0sB=3
(C)cotB=3
5
(D)tanB
3.在平面直角坐标系x0y中,对于抛物线y=-(x-20)+25,下列叙述正确的是(▲)
(A)抛物线有最低点,最低点的坐标是(20,25):
(B)抛物线有最高点,最高点的坐标是(-20,25):
(C)抛物线有最高点,最高点的坐标是(20,25):
(D)抛物线有最低点,最低点的坐标是(-20,25).
4.下列说法中,正确的是(▲)
(A)两个停腰三角形一定相似:
(B)两个直角三角形一定相似:
(C)含45°角的两个等腰三角形一定相似:
(D)含105°角的两个等腰三角形一定相似,
5.在△ABC中,点D,E分别是边AB,AC的中点,下列结论中,错误的是(▲)
(A)△ADE∽△ABC:
《B)S。Aoe三25c
(C)DE=÷BC:
(D)DE∥BC.
6.己知二次函数y=∫(x)的图像是开口向上的抛物线,抛物线的对称轴在y轴右侧.当
抛物线与x轴两交点的距离为9时,若∫(-5)、∫(-)、∫(4)、∫(7)这四个函数值中有且
只有一个值不大于0,那么在这四个函数值中,值不大于0是(▲)
(A)f(-5):
(B)(-):
(c)f(4):
(D)f(7)·.
二、填空题(本大题共12题,每题4分,满分48分)
7.已知a、b是不等于0的实数,7a=5b,那么a+b
b
8.已如f(x)=4x-1.R么(2=▲_
9.将二次函&y=x2-4x+3化成y=a(+m)+k的形式为▲_
10.对七M中阳风际进门博建久(向你进博公)于2024年11月5日至10日E四家么展中心
(上将)风承深办.以历时代、共京宋来“为上题,是世界上首个以沮口为主题的四凉级博跑
会.小海在地图上(图1)测恨他汉回家会展中心(上海)的死离为2.6四米。那么峭历
小海计尊出他家与回家会展中心(上抑)的实际见滴为▲千米,
计自自
量
I12000030
图1
图2
图3
I1.在△ABC中,点D,E分别在边AB.AC上,添加一个条件使△ADE∽△ACB(项
点A、D、E分别与顶点A、C、B对应),这个条件可以是▲·(写出一种情况即可)
I2.(涧孔成侬)如图2,AB∥AB,物像AB所在正方体的面与平面ABAB垂直,根
据图中尺寸,己知物像AB的长为4,那么物AB长为▲·
13.已知两个相似三角形的一组对应边长分别是5埏米和2厘米,如果这组对应边上的高的
长度相差2.4厘米,那么这两条高的长度和为▲皿米,
14.在△ABC中,如果AB=AC,这个三角形的重心为点G,设G=a,GA=b,那么
向耻BC用向a、五丧示为▲一
15.如图3,一座大极前的残疾人酒道是斜坡。用AB丧示,沿着通道走32米可进入楼厅,
楼厅比楼外的地面高0.4米,那么残疾人通道的坡度为▲·(结果保留根号的形式)
16.来校初三致学活动小组在利用尺规把线段AB分割成两条线段.
(I)过点B作BC1AB,使BC=AB.(2)联结AC,在线段CA上藏取CD=CB.
(3)在线段AB上被取AE=AD.那么AE
=▲
BE
I7,在矩形ABCD中,AB=5,BC=I3,点E在边DC上,将矩形ABCD沿AE翻折,
点D怡好弦在边BC上的点F处,那么EC的长为▲、
18.在平面直角坐标系x0y中,将抛物线(:y=ax2+bx+c(其中a、b、c是常数,且
a≠0),以原点为中心,旋转180°得抛物线12,则称12是1的“中心对称抛物线”.己知抛
物线=x-3x-4,将抛物线y向左平移n个单位长度,与x轴的交点从左到右依次为A、
B.将抛物线y的中心对称抛物线”,向右也平移n个单位长度,与x轴的交点从左到右依
次为C、D.当线段BC是线段AB、BD的比例中项时,n的值为▲
同课章节目录
